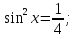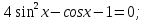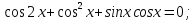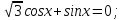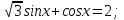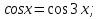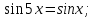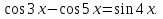Конспект урока по Математике "Тригонометрические уравнения"
Тема урока «Тригонометрические уравнения» (2 часа)
Тригонометрия по традиции занимает большое место в материалах конкурсных экзаменов в вузы; чтобы научиться уверенно решать экзаменационные задачи по тригонометрии, нужна тренировка. В школьном курсе подробно изучаются три основных метода решения тригонометрических уравнений – метод введения нового неизвестного, что позволяет свести уравнение к квадратному; разложение на множители; метод введения вспомогательного аргумента.
В своем уроке я рассмотрела решение тригонометрических уравнений, опираясь на методы их решения в наиболее доступной последовательности изложения материала.
Предварительная подготовка к уроку. Учащиеся должны знать следующие темы: «Основные тригонометрические тождества», «Формулы сложения и их свойства», «Сумма и разность синусов. Сумма и разность косинусов», «Простейшие тригонометрические уравнения».
Цели урока. Образовательная: формирование умений применять полученные раннее знания; сопоставлять, анализировать, делать выводы; отработка умения решать уравнения.
Воспитательная: формирование интереса к познавательному процессу.
Развивающая: развитие наблюдательности, памяти, логического мышления.
Оборудование: Таблицы «Формулы корней простейших тригонометрических уравнений», «Основные формулы тригонометрии»
Тип урока: урок совершенствования знаний. Объяснение нового материала построено на решении конкретных примеров.
Ход урока.
Организационный момент. Сообщение темы урока; постановка цели урока; сообщение этапов урока.
Изучение нового материала.
Вы уже знакомы с формулами корней простейших тригонометрических уравнений
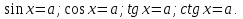 К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.
К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.
Уравнения, сводящиеся к квадратным.
Задача 1. Решить уравнение 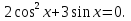
Заменим 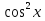 на
на 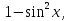 получим
получим
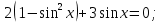
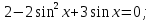 это уравнение является квадратным относительно
это уравнение является квадратным относительно 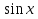 .
.
Обозначим 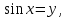 получим
получим 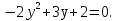
Отсюда 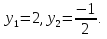
Таким образом, решение исходного уравнения свелось к решению простейших
уравнений 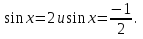
Уравнение 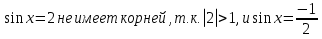
имеет корни 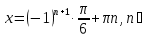 N.
N.
Ответ: 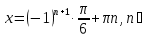 N.
N.
Однородные уравнения.
Задача 2. Решить уравнение 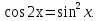
Заменим 
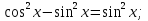
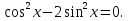

Поделив уравнение на  получим
получим
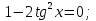
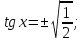
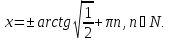
Ответ: 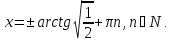
Напомним, что при делении уравнения на выражение, содержащее неизвестное, могут быть потеряны корни. Поэтому нужно проверить, не являются ли корни уравнения 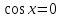 корнями данного уравнения.
корнями данного уравнения.
Задача 3. Решить уравнение 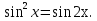
Заменим 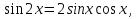

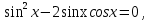
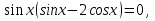
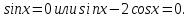
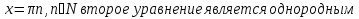

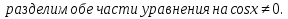
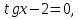
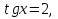
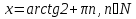
Ответ: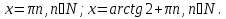
Вынесение общего множителя за скобки.

Задача 4. Решить уравнение 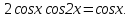
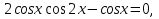
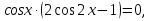
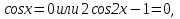
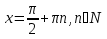
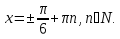
Ответ: 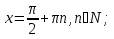
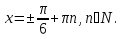
Преобразование суммы в произведение.
Используем формулы 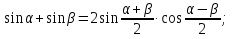
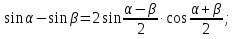
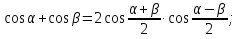
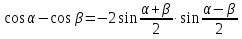 .
.
Задача 5. Решить уравнение 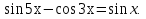
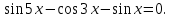
Заменим разность синусов, на произведение, получим уравнение
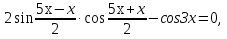
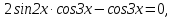
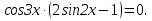
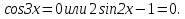
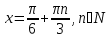
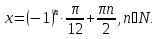
Ответ: 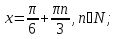
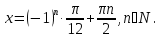
Преобразование произведения в сумму.
Используем формулы 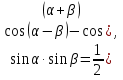
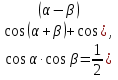
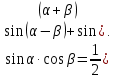
Задача 6. Решить уравнение 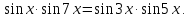
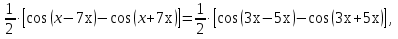
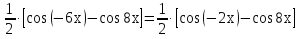 ,
,
Умножим обе части уравнения на 2 и учитывая, что 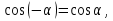 получим
получим
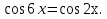
 Заменим разность косинусов произведением.
Заменим разность косинусов произведением.
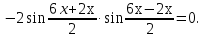
Отсюда 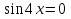 или
или 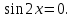
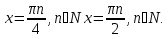
Так как первая серия решений включает в себя вторую серию решений при 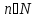 , то в
, то в
ответе записываем только 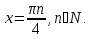 (Для наглядности рассмотреть решение
(Для наглядности рассмотреть решение
на единичной окружности)
Ответ: 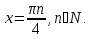
Введение вспомогательного угла.
Используем формулы 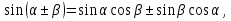
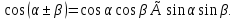
Рассмотрим уравнение 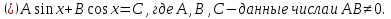
Разделим обе части уравнения (*) на 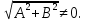
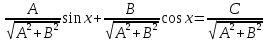 .
.
Обозначим 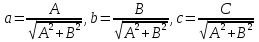 .
.
Так как 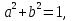 то можно подобрать такой угол α, что
то можно подобрать такой угол α, что 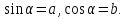
Тогда исходное уравнение примет вид
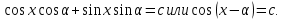
Если подобрать такой угол 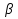 , что a =
, что a = 
в виде 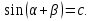
Задача 7. Решить уравнение 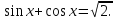
Разделим правую и левую часть на 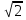 .
.
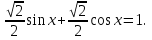 Так как
Так как 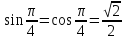 ,
,
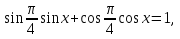
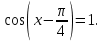
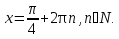
Ответ: 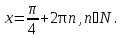
Замечание: Вспомогательный угол вводится, если слагаемое есть 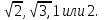
Решение уравнений с помощью формул приведения.
Задача 8. Решить уравнение 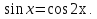
Заменим 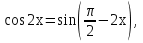 получим уравнение
получим уравнение
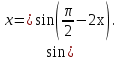
Замечание: Из равенства синусов не следует равенство аргументов.
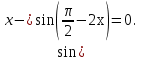 Разность синусов заменим произведением.
Разность синусов заменим произведением.
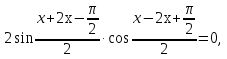
отсюда 
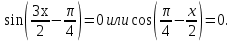
Это простейшие тригонометрические уравнения, которые имеют решения
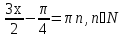
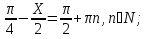
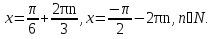
Ответ:
Понижение степени.
Используем формулы 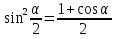 ;
;
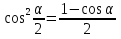 .
.
Задача 9. Решить уравнение 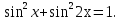
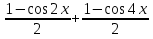 =1, умножим уравнение на 2
=1, умножим уравнение на 2
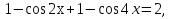

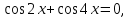 заменим сумму произведением и получим
заменим сумму произведением и получим
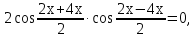
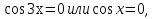
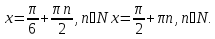
Ответ: 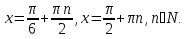
Введение новой переменной.
Задача 10. Решить уравнение 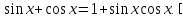
Пусть 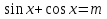 , возведем правую левую часть равенства в квадрат,
, возведем правую левую часть равенства в квадрат,
тогда 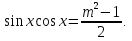
Получим уравнение 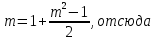
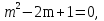
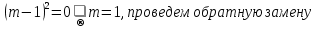
 .
.
Умножим уравнение на 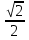 , введем вспомогательный угол
, введем вспомогательный угол
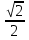
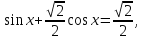
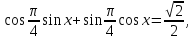
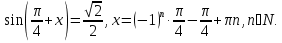
Ответ: 
Универсальная подстановка.
Используем формулы
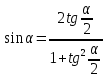 ,
, 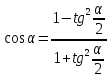 ,
, 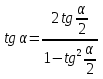 .
.
Замечание: При использовании универсальной подстановки может быть потеряна серия ответов 
Задача 11. Решить уравнение 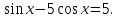
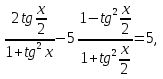 пусть
пусть 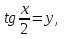 тогда
тогда
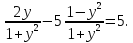
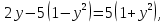 отсюда y = 5.
отсюда y = 5.
Проведем обратную замену 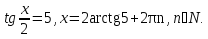
Проверка, если 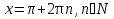 , то
, то
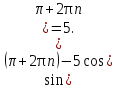

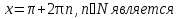
корнем данного уравнения.
Ответ: 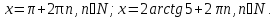
Итог урока: С какими способами решения уравнений сегодня познакомились?
Домашнее задание: Внимательно разобрать материал лекции.
Решить уравнение:

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ