1. Построим поле корреляции (на отдельном листе) и сформулируем гипотезу о форме связи, предполагая, что генеральное уравнение регрессии – линейное: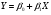

Поле корреляции

y = 0,0443x + 369,31

R

2

= 0,0177

10

110

210

310

410

510

610

710

750

900

1050

1200

1350

1500

1650

1800

2. Найдем оценки b₀ и b₁ параметров модели парной линейной регрессии 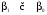по следующим формулам:

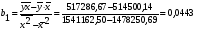
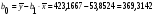
Тогда уравнение эмпирической линии регрессии (линии тренда) имеет вид:

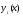= 369,3142 + 0,0443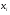

3. С надежностью 0,95 проверим значимость оценок b₀ и b₁ теоретических коэффициентов регрессии 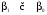с помощью t-статистики Стьюдента и сделаем соответствующие выводы о значимости этих оценок.

Для уровня значимости =0,05 и числа степеней свободы к=n-2=12-2=10 критерий Стьюдента равен .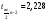

Дисперсии средние квадратичные отклонения коэффициентов b₀ и b₁ уравнения регрессии определим из равенств с использованием результатов табл. 2.

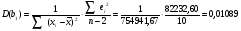
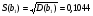
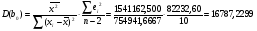
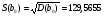
Для определения статистической значимости коэффициентов b₀ и b₁ найдем t – статистики Стьюдента:

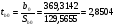
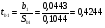
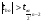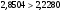Сравнение расчетных и табличных величин критерия Стьюдента показывает, что или и 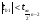или 0.4244<2,2280, т.е. с надежностью 0,95 оценка b₀ теоретического коэффициента регрессии ₀ статистически незначима, оценка b₁ теоретического коэффициента регрессии ₁ статистически значима.

4. С надежностью 0,95 определим интервальные оценки теоретических коэффициентов 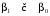регрессии и сделаем соответствующие выводы о значимости этих оценок.

Доверительные интервалы для этих коэффициентов равны:

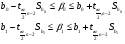
Подставив числовые значения, значения коэффициентов b₀ и b₁, их средние квадратичные отклонения и значение для t имеем:

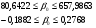
Так как точка 0 (ноль) лежит внутри доверительного интервала, то интервальная оценка коэффициента ₁ статистически незначима.

5. Определим коэффициент детерминации R² и коэффициент корреляции r_xy и сделаем соответствующие выводы о качестве уравнения регрессии.

Определяем дисперсии и средние квадратичные отклонения независимого X и результативного Y факторов:

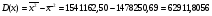
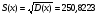
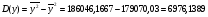
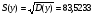
Тесноту связи между переменными X и Y определяем через ковариацию и коэффициент корреляции.

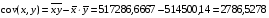
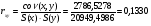
Величина r_xy=0,1330 , близка к 1, что характеризует слабую линейную связь между независимым и результативным признаками.

Для определения коэффициента детерминации воспользуемся результатами расчетов таблицы 2.

По таблице 2 найдем:

• общую ошибку (столбец 11):

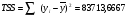
• ошибку объясняемую регрессией (столбец 13)

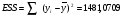
• остаточную ошибку (столбец 9)

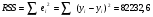
Причем имеем TSS=RSS+ESS

Тогда коэффициент детерминации равен

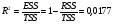
Полученная величина коэффициента детерминации свидетельствует о том, что необъясненная ошибка составляет более 98 процентов от общей ошибки.

6. Проверим при уровне значимости 0,05 значимость уравнения регрессии с помощью F статистики Фишера и сделаем соответствующие выводы о значимости уравнения регрессии.

Статистика Фишера вычисляется по формуле: .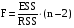

Имеем F = (1481,071/82232,60)·10=0,1801

Найдем для заданной доверительной вероятности 0,05 критическое значение статистики Фишера:

По таблице .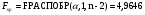

Имеем F < F_кр, поэтому уравнение незначимо с надежностью 0,95.

7. Оценим с помощью средней ошибки аппроксимации качество уравнения регрессии.

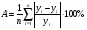
A=14,934%.

Судя по величине средней ошибки, качество уравнения регрессии среднее.

8. Рассчитаем прогнозное значение результата Yp, если прогнозное значение фактора Xр увеличится на 15% от его среднего уровня.

Хр = 1,15*Хср = 1,15*1215,8333 = 1398,2083.

Прогнозируемую величину y_p определяем из равенства:

9. С уровнем значимости 0,05 определим интервальную оценку условного математического ожидания Уp для вычислинного значения Хp.

Дисперсия математического ожидания прогнозируемой величины y_p равна

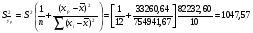
Среднее квадратичное отклонение математического ожидания прогнозируемой величины равно

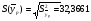
С уровнем значимости =0,05 доверительный интервал для условного математического ожидания yp при данном x_p равен:

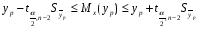
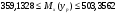
10. С надежностью 0,95 определим доверительный интервал значения Уp для вычислинного значения Хp

Имеем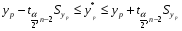

Дисперсия конкретного значения прогнозируемой величины y_p равна

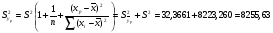
Среднее квадратичное отклонение ожидаемой прогнозируемой величины y_p равно

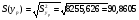
Тогда получим,

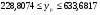
11. Найдем основные регрессионные характеристики используя функцию Регрессия (У,Х) из надстройки "Анализ данных". Уровень надежности установим 95%.

ВЫВОД ИТОГОВ

Регрессионная статистика

Множественный R

0,133012

R-квадрат

0,017692

Нормированный R-квадрат

-0,080539

Стандартная ошибка

90,68219

Наблюдения

12

Дисперсионный анализ

 

df

SS

MS

F

Значимость F

Регрессия

1

1481,071

1481,071

0,180108

0,680266

Остаток

10

82232,6

8223,26

Итого

11

83713,67

 

 

 

 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Нижние 95%

Верхние 95%

Y-пересечение

369,3142

129,5655

2,850405

0,017238

80,62417

658,0043

Переменная X 1

0,044293

0,104368

0,424391

0,680266

-0,188253

0,276838

Таблица 2

№

x

y

xy

x^2

y^2

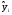
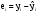
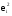
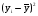
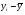
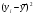
1

2

3

4

5

6

7

8

9

10

11

12

13

14

1

1305

420

548100

1703025,0

176400

427,116

-7,12

50,638

7951

10,03

3,949

15,598

0,017

2

1440

512

737280

2073600,0

262144

433,096

78,90

6225,9

50251

7891,36

9,929

98,584

0,154

3

1230

430

528900

1512900,0

184900

423,794

6,21

38,512

201

46,69

0,627

0,394

0,014

4

1275

230

293250

1625625,0

52900

425,787

-195,8

38332,6

3501

37313,4

2,621

6,868

0,851

5

1700

505

858500

2890000,0

255025

444,612

60,39

3646,75

234417

6696,69

21,445

459,888

0,0120

6

1480

402

594960

2190400,0

161604

434,867

-32,87

1080,26

69784

448,03

11,701

136,905

0,082

7

1305

430

561150

1703025,0

184900

427,116

2,88

8,316

7951

46,69

3,949

15,598

0,007

8

895

400

358000

801025,0

160000

408,956

-8,96

80,212

102904

536,69

-14,211

201,940

0,022

9

775

410

317750

600625,0

168100

403,641

6,36

40,436

19434

173,36

-19,526

381,251

0,016

10

1000

585

585000

1000000,0

342225

413,607

171,39

29375,6

46584

26190,0

-9,560

93,390

0,293

11

1035

370

382950

1071225,0

136900

415,157

-45,16

2039,16

32701

2826,69

-8,010

64,153

0,122

12

1150

384

441600

1322500,0

147456

420,251

-36,25

1314,11

4334

1534,03

-2,916

8,503

0,094

∑

14590

5078

6207440

18493950,0

2232554

5078,0

0,0

82232,6

754942

83713,7

0,0000

1481,071

1,7921

Ср.
знач

1215,833

423,1667

517286,67

1541162,5

186046,17

-

-

-

-

6976,1

-

123,4226

0,1493