Криволинейный интеграл первого рода

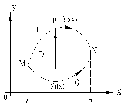
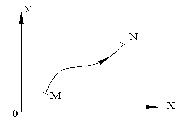
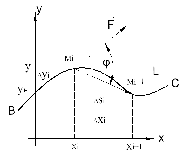
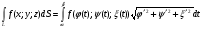
Криволинейный интеграл второго рода

1. Задача приводящая к понятию криволинейного интеграла.

Определение криволинейного интеграла по координатам.

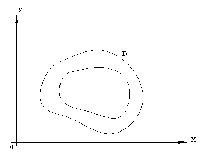
2. Свойства криволинейного интеграла (рис. 1).

3. Вычисления

а)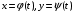

б)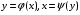

Рис. 1

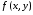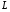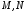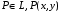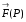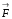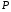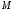Займемся обобщением понятия определенного интеграла на случай когда путь интегрирования – кривая -кривая , , . Т/н. А-работу силы при перемещении точки от к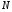

1. Разобьем на n частей :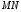

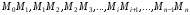
Обозначим 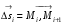вектор- хорда 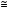дуге.

Пусть 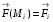предположим, что н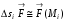а тогда

Работа 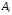вдоль дуги 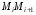вычисляется как скалярное произведение векторов 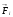и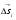

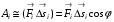
Пусть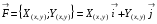

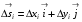
Тогда: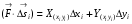

Работа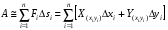

Если 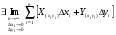, то этот предел примем за работу А силы 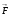при движении точки 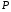по кривой 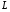от точки 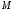до точки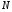

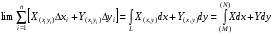
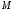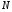,-не числа, а точки концы линии .

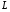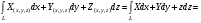
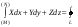
1. Свойства:

1⁰ 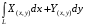определяется

а) подынтегральным выражением

б) формой кривой интегрирования.

в) указанием направления интегрирования (рис. 2).

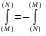
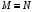
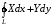
Рис. 2

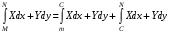
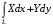-можно рассматривать как интеграл от векторной функции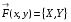

Тогда 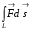- если 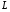-замкнутая то 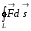-называют циркуляцией вектора 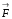по контуру .

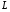3⁰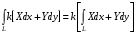

4⁰ 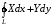не зависит от того какую точку 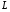взять за начало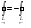

Вычисление криволинейного интеграла

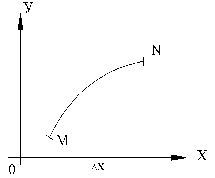
Криволинейные интегралы вычисляются сведением их к обыкновенным интегралам по отрезку прямой (рис. 3).

Рис. 3

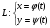-гладкая кривая.

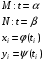
1. Если 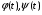-непрерывны, 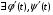-непрерывные.

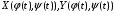-непрерывны п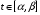о , то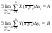

Пределы А и В не зависят ни от способа деления 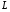на 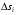, ни от вектора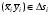

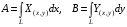
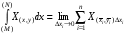
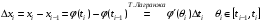
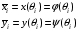
Следовательно: .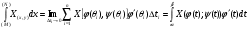

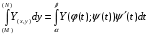
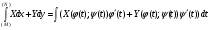
2. В случае: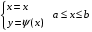

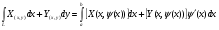
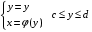
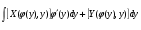
1. Формула Грина.

2. Условие независимости криволинейного интеграла от пути интегрирования.

3. Полный дифференциал.

Связь между определенным и криволинейным интегралами.

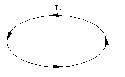
Пусть дано область D, замкнутая, ограниченная линией 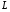(рис. 4).

интеграл криволинейный грин формула

Рис. 4

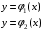непрерывны на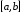

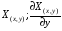- определена и непрерывна в замкнутой области D.

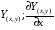- определена и непрерывна в замкнутой области D. Тогда

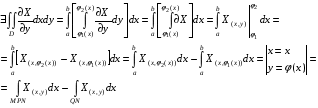
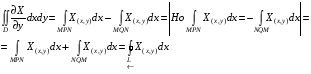
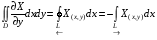
Аналогично

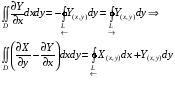
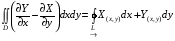-Формула Грина.

В частности: вычисление площадей фигур с помощью двойного интеграла.

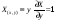
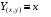
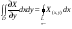
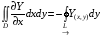
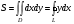
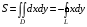
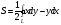
Пример.

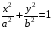
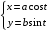
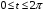
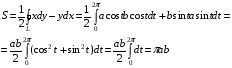
Условие независимости криволинейного интеграла от пути интегрирования

Рис. 5

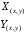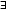- непрерывные частные производные в 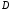(рис. 5).

Каковы условия независимости криволинейного интеграла от пути интегрирования?

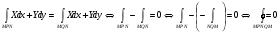
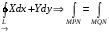
Теорема: 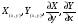-непрерывны в области 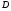, тогда для того, чтобы

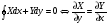в 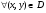(рис. 6)

Рис. 6

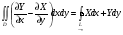
Пусть

Обратно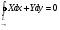

Т.д.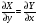

Пусть 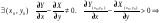из непрерывност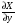и и

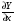
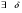-окрестность точки 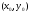такая что 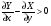в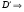

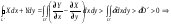предположение неверно. ч.т.д.

Замечание.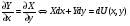

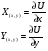
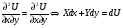
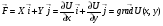
Определение. Функция 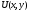-градиент которой есть вектор силы 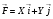называется потенциалом вектора .

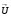Тогда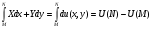

Вывод: Криволинейный интеграл от полного дифференциала не зависит от формы пути интегрирования.

Литература

1. Ильин В.А., Садовничий В.А., Сендов Б.Х. Математический анализ. 1-2 том. Изд. МГУ, 1989 г.

2. Виноградова И.А., Олексич С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу. Часть 1,2 Изд. МГУ. Серия классический университетский учебник 250 летию МГУ 2005 г.

3. Шилов Г.Е. Математический анализ. Часть 1,2. Москва. Изд. Лань. 2002 г. – 880 с.

4. Лунгу К.Н. Сборник задач по математике. Часть 1,2. Москва. Айрис пресс 2005 г.