Математическая статистика
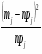
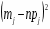
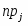
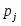
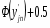
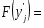
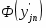
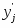
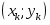
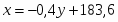
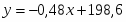
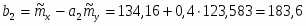
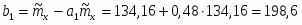
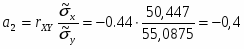
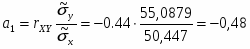
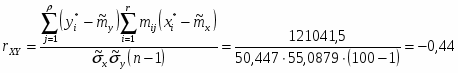
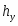
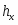
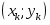
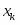
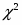
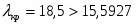
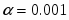
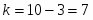
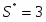
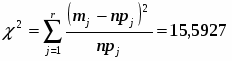
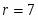
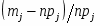
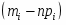
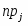
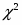
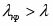
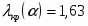
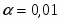
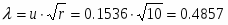
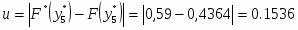
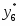
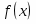
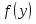
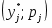
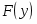
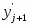
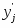
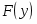
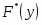
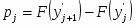
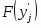
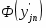
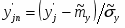
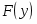
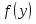
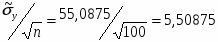
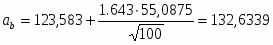
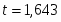
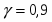
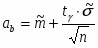
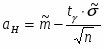
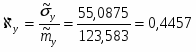
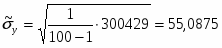
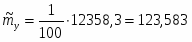
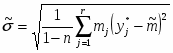
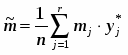
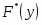
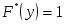
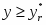
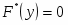
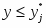
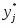
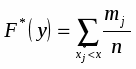
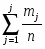
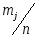
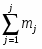
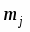
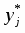
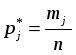
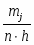
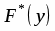
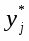
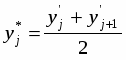
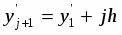
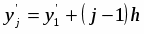
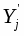
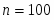
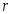
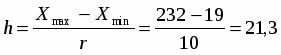
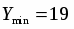
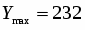
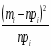
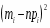
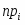
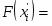
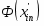
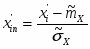
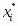
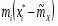
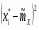
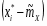
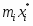
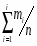
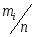
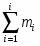
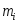
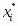
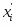
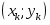
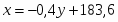
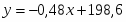
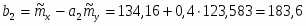
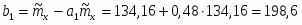
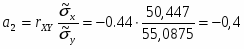
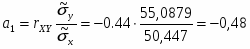
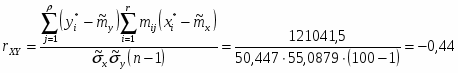
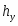
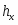
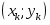
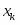
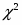
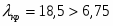
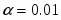
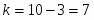
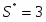
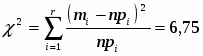
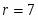
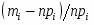
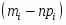
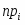
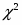
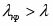
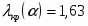
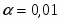
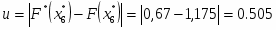
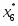
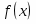
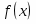
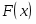
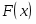
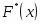
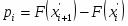
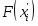
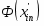
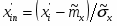
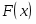
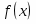
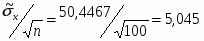
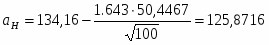
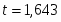
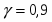
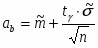
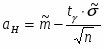
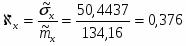
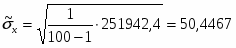
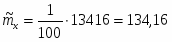
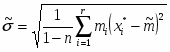
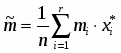
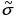
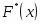
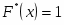
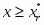
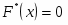
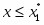
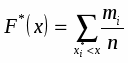
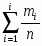
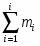
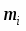
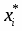
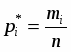
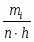
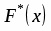
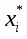
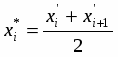
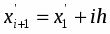
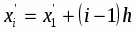
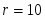
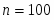
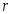
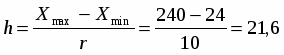
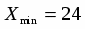
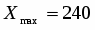Министерство образования и науки Российской Федерации.
Федеральное агентство по образованию.
Государственное образовательное учреждение высшего профессионального
образования.
Самарский государственный технический университет.
Кафедра высшей математике
Курсовая работа
студент
руководитель: .
ассистент: Н.
Самара
2004 г.
Пусть случайные величины Х и Y принимают значение, приведённые в таблице 1.
Таблица 1
Х
Y
X
Y
X
Y
X
Y
70
60
97
62
27
25
57
35
73
60
96
85
43
25
60
34
80
55
67
34
24
19
92
85
41
30
80
80
24
20
93
75
56
25
82
78
27
19
100
65
103
92
90
80
100
90
120
115
104
92
120
92
101
110
120
90
104
114
115
115
102
112
92
75
93
62
123
115
145
118
123
112
118
115
127
120
150
118
123
100
121
92
127
117
150
119
96
72
117
92
130
120
150
120
130
119
112
110
135
125
131
120
142
119
96
78
153
125
132
142
142
140
127
120
153
142
202
175
145
144
130
125
153
135
202
173
157
150
130
140
153
145
205
202
180
180
130
119
162
172
180
202
180
200
150
140
165
165
188
225
180
175
140
120
165
150
210
220
180
190
140
125
165
146
221
225
200
200
162
170
170
152
225
220
200
175
155
170
170
165
225
230
240
228
157
160
154
170
227
232
240
232
157
165
154
165
237
232
132
140
1) Находим, что
Тогда длина интервала группирования
- число интервалов (разрядов), неформализован и зависит от объёма и степени однородности выборки. При ,
2) Находим границы величины
,
3) Находим значение представителей
- середина i-того интервала.
4) Для графического описания выборки по условиям задания необходимо построить гистограмму относительных частот (рис. 1) и эмпирическую функцию распределения (рис. 2)
а) На гистограмме относительных частот высота прямоугольников выбирается равной , основания прямоугольников соответствуют интервалам разбиения. Площадь i-того прямоугольника равна относительной частоте наблюдений, попавших в i-тый интервал.
Составляем таблицу частот группированной выборки (табл. 2), содержащую столбцы с номерами интервала i, значениями нижней границы (начала интервала) и представителя интервала , числами значений в i-том интервале , накопленной частоты , относительной частоты , накопленной относительной частоты . Число строк таблицы равно числу интервалов r.
Рис. 1. Гистограмма относительных частот
б) Эмпирическая функция распределения определяется по значениям накопленных относительных частот представителей разрядов:
Функция представляет собой кусочно-постоянную функцию, имеющие скачки в точках, соответствующих серединам интервалов группировки , причём при , и при
Рис. 2. Эмпирическая функция распределения
5) Составленную ранее таблицу частот группированной выборки (табл. 2) дополняем таблицей расчёта числовых значений и . Она содержит результаты промежуточных вычислений по формулам
6) После заполнения таблицы 2 рассчитываем значение числовых оценок:
7) Определяем коэффициент вариаций
8) Определяем границы доверительного интервала для математического ожидания по формулам
При заданной доверительной вероятности по таблицам распределения Стьюдента , поэтому имеем
9) Среднеквадратичное отклонение оценки математического ожидания случайной величины Х равно
10) По виду гистограммы выдвигаем гипотезу Н0 о подчинении случайной величины Х нормальному закону распределения. Для построения теоретической функции и составляем таблицу значений (таблица 3) нормальной величины , определяем функцию Лапласа , значения функции распределения на концах отрезков и вероятность попадания в i-тый интервал по формуле
11) Рисунок 2 с эмпирической функцией распределения дополняем теоретической функцией F(x), значения которой найдены на концах интервалов.
Рис. 3. Эмпирическая , теоретическая функция распределения.
12) Для проверки согласия выдвинутой гипотезы о о законе распределения экспериментальным данным находим вероятность попадания опытных данных в i-тый интервал от до на основе полученных значений функции на границах интервалов. На построенную раньше гистограмму наносим точки с координатами и соединяем их плавными линиями (Рис. 4). Сравнивая вид гистограммы и плотность распределения, необходимо убедиться в их адекватности, близости их характеров.
Рис. 4. Гистограмма относительных частот и теоретическая плотность вероятности .
13) При количественной оценке меры близости эмпирического и теоретического законов распределения можно использовать критерии Пирсона или Колмогорова.
а) по критерию Колмогорова:
Максимальное значение модуля разности между значениями эмпирической и теоретической функциями(см. рис. 3) наблюдается в точке, близкой к представителю . Тогда
Вычисляем величину
где r – объём выборки из представителей интервалов
, следовательно . Так как , поэтому гипотеза о нормальном распределении по критерию Колмогорова принимается как не противоречащая опытным данным.
б) Для вычисления таблицу 3 дополняем промежуточными результатами ,, . Объединяем 1,2,3 и 9,10. Тогда . Получаем, что
Для нормального закона распределения . Тогда число степеней свободы . При имеем . Поэтому гипотеза по критерию Пирсона принимается.
14) Составляем точечную диаграмму в декартовой (рис. 5) системе координат, где по оси абсцисс откладываем значение , а по оси ординат - . Пары значений представляем на диаграмме в виде точек. На диаграмму наносим сетку равноотстоящих горизонтальных и вертикальных прямых. Расстояние между двумя вертикальными прямыми выражает длину интервала по оси абсцисс, а расстояние между горизонтальными прямыми – длину интервала по оси ординат.
15) Для вычисления коэффициента корреляции составляется корреляционная таблица (таблица 4). В последние две строки заносятся промежуточные результаты для вычисления точечной оценки коэффициента корреляции
16) Находим
Следовательно, линейные приближения к регрессиям имеют вид:
На рисунке 3 представлены точечная диаграмма и линии регрессии X на Y и Y на X. Расположение точек на диаграмме и небольшое значение коэффициента корреляции указывают на слабую коррелированность случайных величин X и Y между собой.
Таблица 2
№ интервала
1
24
34,8
6
6
0,06
0,06
208,8
-99,36
9872,41
59234,46
2
45,6
56,4
4
10
0,04
0,1
225,6
-77,76
6046,618
24186,47
3
67,2
78
5
15
0,05
0,15
390
-56,16
3153,946
15769,73
4
88,8
99,6
16
31
0,16
0,31
1593,6
-34,56
1194,394
19110,3
5
110,4
121,2
21
52
0,21
0,52
2545,2
-12,96
167,9616
3527,194
6
132
142,8
15
67
0,15
0,67
2142
8,64
74,6496
1119,744
7
153,6
164,4
13
80
0,13
0,8
2137,2
30,24
914,4576
11887,95
8
175,2
186
6
86
0,06
0,86
1116
51,84
2687,386
16124,31
9
196,8
207,6
7
93
0,07
0,93
1453,2
73,44
5393,434
37754,04
10
218,4
229,2
7
100
0,07
1
1604,4
95,04
9032,602
63228,21
11
240
Сумма
100
1
13416
251942,4
Таблица 3
№ интервала
1
24
-2,18368
-0,4854
0,0146
0,0255
2,55
3,8025
0,224336
2
45,6
-1,75551
-0,4599
0,0401
0,0517
5,17
3
67,2
-1,32733
-0,4082
0,0918
0,0923
9,23
4
88,8
-0,89916
-0,3159
0,1841
0,1351
13,51
6,2001
0,458927
5
110,4
-0,47099
-0,1808
0,3192
0,1648
16,48
20,4304
1,239709
6
132
-0,04282
-0,016
0,484
0,164
16,4
1,96
0,119512
7
153,6
0,385355
0,148
0,648
0,143
14,3
1,69
0,118182
8
175,2
0,813527
0,291
0,791
0,1015
10,15
17,2225
1,696798
9
196,8
1,241699
0,3925
0,8925
0,06
6
25,8064
2,893094
10
218,4
1,669871
0,4525
0,9525
0,0292
2,92
11
240
2,098043
0,4817
0,9817
Пусть случайные величины Х и Y принимают значение, приведённые в таблице 1.
Таблица 1
Х
Y
X
Y
X
Y
X
Y
70
60
97
62
27
25
57
35
73
60
96
85
43
25
60
34
80
55
67
34
24
19
92
85
41
30
80
80
24
20
93
75
56
25
82
78
27
19
100
65
103
92
90
80
100
90
120
115
104
92
120
92
101
110
120
90
104
114
115
115
102
112
92
75
93
62
123
115
145
118
123
112
118
115
127
120
150
118
123
100
121
92
127
117
150
119
96
72
117
92
130
120
150
120
130
119
112
110
135
125
131
120
142
119
96
78
153
125
132
142
142
140
127
120
153
142
202
175
145
144
130
125
153
135
202
173
157
150
130
140
153
145
205
202
180
180
130
119
162
172
180
202
180
200
150
140
165
165
188
225
180
175
140
120
165
150
210
220
180
190
140
125
165
146
221
225
200
200
162
170
170
152
225
220
200
175
155
170
170
165
225
230
240
228
157
160
154
170
227
232
240
232
157
165
154
165
237
232
132
140
1) Находим, что
Тогда длина интервала группирования
- число интервалов (разрядов), неформализован и зависит от объёма и степени однородности выборки. При ,
2) Находим границы величины
,
3) Находим значение представителей
- середина j-того интервала.
4) Для графического описания выборки по условиям задания необходимо построить гистограмму относительных частот (рис. 1) и эмпирическую функцию распределения (рис. 2)
а) На гистограмме относительных частот высота прямоугольников выбирается равной , основания прямоугольников соответствуют интервалам разбиения. Площадь j-того прямоугольника равна относительной частоте наблюдений, попавших в j-тый интервал.
Составляем таблицу частот группированной выборки (табл. 2), содержащую столбцы с номерами интервала j, значениями нижней границы (начала интервала) и представителя интервала , числами значений в j-том интервале , накопленной частоты , относительной частоты , накопленной относительной частоты . Число строк таблицы равно числу интервалов r.
Рис. 1. Гистограмма относительных частот
б) Эмпирическая функция распределения определяется по значениям накопленных относительных частот представителей разрядов:
Функция представляет собой кусочно-постоянную функцию, имеющие скачки в точках, соответствующих серединам интервалов группировки , причём при , и при
Рис. 2. Эмпирическая функция распределения
5) Составленную ранее таблицу частот группированной выборки (табл. 2) дополняем таблицей расчёта числовых значений и . Она содержит результаты промежуточных вычислений по формулам
6) После заполнения таблицы 2 рассчитываем значение числовых оценок:
7) Определяем коэффициент вариаций
8) Определяем границы доверительного интервала для математического ожидания по формулам
При заданной доверительной вероятности по таблицам распределения Стьюдента , поэтому имеем
9) Среднеквадратичное отклонение оценки математического ожидания случайной величины Y равно
10) По виду гистограммы выдвигаем гипотезу Н0 о подчинении случайной величины нормальному закону распределения. Для построения теоретической функции и составляем таблицу значений (таблица 3) нормальной величины , определяем функцию Лапласа , значения функции распределения на концах отрезков и вероятность попадания в i-тый интервал по формуле
11) Рисунок 2 с эмпирической функцией распределения дополняем теоретической функцией F(y), значения которой найдены на концах интервалов.
Рис. 3. Эмпирическая , теоретическая функция распределения.
12) Для проверки согласия выдвинутой гипотезы о о законе распределения экспериментальным данным находим вероятность попадания опытных данных в j-тый интервал от до на основе полученных значений функции на границах интервалов. На построенную раньше гистограмму наносим точки с координатами и соединяем их плавными линиями (Рис. 4). Сравнивая вид гистограммы и плотность распределения, необходимо убедиться в их адекватности, близости их характеров.
Рис. 4. Гистограмма относительных частот и теоретическая плотность вероятности .
13) При количественной оценке меры близости эмпирического и теоретического законов распределения можно использовать критерии Пирсона или Колмогорова.
а) по критерию Колмогорова
Максимальное значение модуля разности между значениями эмпирической и теоретической функциями(см. рис. 2) наблюдается в точке, близкой к представителю . Тогда
Вычисляем величину
где r – объём выборки из представителей интервалов
, следовательно . Так как , поэтому гипотеза о нормальном распределении по критерию Колмогорова принимается как не противоречащая опытным данным.
б) Для вычисления таблицу 3 дополняем промежуточными результатами ,, . Объединяем 1,2,3 и 9,10. Тогда . Получаем, что
Для нормального закона распределения . Тогда число степеней свободы . При имеем . Поэтому гипотеза по критерию Пирсона принимается.
14) Составляем точечную диаграмму в декартовой системе координат, где по оси абсцисс откладываем значение , а по оси ординат - . Пары значений представляем на диаграмме в виде точек. На диаграмму наносим сетку равноотстоящих горизонтальных и вертикальных прямых. Расстояние между двумя вертикальными прямыми выражает длину интервала по оси абсцисс, а расстояние между горизонтальными прямыми – длину интервала по оси ординат.
15) Для вычисления коэффициента корреляции составляется корреляционная таблица (таблица 4). В последние две строки заносятся промежуточные результаты для вычисления точечной оценки коэффициента корреляции
16) Находим
Следовательно, линейные приближения к регрессиям имеют вид:
На рисунке 3 представлены точечная диаграмма и линии регрессии X на Y и Y на X. Расположение точек на диаграмме и небольшое значение коэффициента корреляции указывают на слабую коррелированность случайных величин X и Y между собой.
Таблица 2
№ интервала
1
19
29,65
10
10
0,1
0,1
296,5
-93,933
8823,408
88234,08
2
40,3
50,95
3
13
0,03
0,13
152,85
-72,633
5275,553
15826,66
3
61,6
72,25
10
23
0,1
0,23
722,5
-51,333
2635,077
26350,77
4
82,9
93,55
10
33
0,1
0,33
935,5
-30,033
901,9811
9019,811
5
104,2
114,85
26
59
0,26
0,59
2986,1
-8,733
76,26529
1982,898
6
125,5
136,15
10
69
0,1
0,69
1361,5
12,567
157,9295
1579,295
7
146,8
157,45
7
76
0,07
0,76
1102,15
33,867
1146,974
8028,816
8
168,1
178,75
10
86
0,1
0,86
1787,5
55,167
3043,398
30433,98
9
189,4
200,05
4
90
0,04
0,9
800,2
76,467
5847,202
23388,81
10
210,7
221,35
10
100
0,1
1
2213,5
97,767
9558,386
95583,86
11
232
Сумма
100
1
12358,3
300429
Таблица 3
№ интервала
1
19
-1,89849
-0,4713
0,0287
0,0368
3,68
8,4681
0,421508
2
40,3
-1,51183
-0,4345
0,0655
0,0659
6,59
3
61,6
-1,12517
-0,3686
0,1314
0,0982
9,82
4
82,9
-0,73852
-0,2704
0,2296
0,1336
13,36
11,2896
0,84503
5
104,2
-0,35186
-0,1368
0,3632
0,1488
14,88
123,6544
8,310108
6
125,5
0,034799
0,012
0,512
0,1508
15,08
25,8064
1,7113
7
146,8
0,421457
0,1628
0,6628
0,1282
12,82
33,8724
2,642153
8
168,1
0,808114
0,291
0,791
0,092
9,2
30,6916
1,6626
9
189,4
1,194772
0,383
0,883
0,0599
5,99
10
210,7
1,58143
0,4429
0,9429
0,0327
3,27
11
232
1,968087
0,4756
0,9756
Сумма
13,5927
Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ