Математическое програмирование
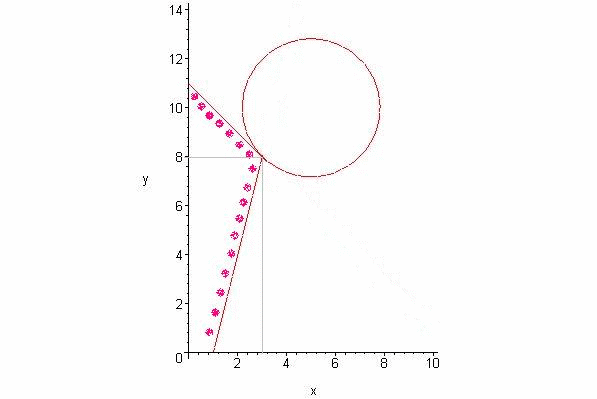
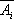
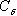
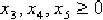
 Математическое программирование
Математическое программирование
Задача 1
Для производства двух видов изделий А и В используется три типа технологического оборудования. Для производства единицы изделия А оборудование первого типа используется 2 часа, оборудование второго типа – 1 час, оборудование третьего типа – 3 часа. Для производства единицы изделия В оборудование первого типа используется 2 часа, оборудование второго типа – 2 часа, оборудование третьего типа – 1 час.
На изготовление всех изделий предприятие может использовать оборудование первого типа не более чем 48 часа, оборудование второго типа – 38 часов, оборудование третьего типа – 54 часов.
Прибыль от реализации единицы готового изделия А составляет 2 денежные единицы, а изделия В – 3 денежные единицы.
Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу симплекс-методом путем преобразования симплекс-таблиц. Дать геометрическое истолкование задачи, используя для этого ее формулировку с ограничениями – неравенствами.
Решение.
Данная задача является задачей линейного программирования. Под планом производства понимается: сколько изделий А и сколько изделий В надо выпустить, чтобы прибыль была максимальна.
Прибыль рассчитывается по формуле: 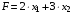
Запишем математическую модель задачи:
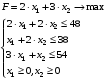
Решим данную задачу графически.
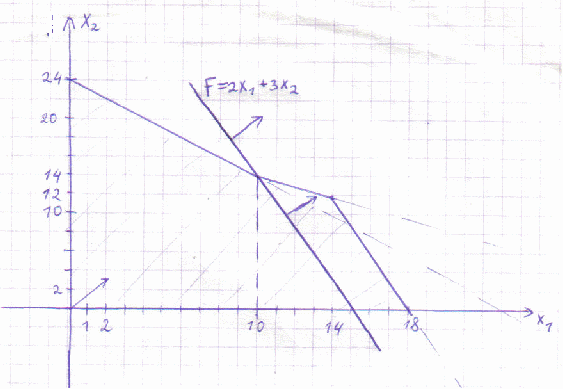
Для этого построим на плоскости области, описываемые ограничениями-неравенствами, и прямую 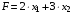 , которая называется целевой функцией.
, которая называется целевой функцией.
Три записанных выше неравенства ограничивают на плоскости многоугольник, ограниченный слева и снизу координатными осями (т.к. искомое количество изделий положительно).
График целевой функции передвигается в направлении, обозначенном стрелкой (в направлении своего градиента), до тех пор, пока не достигнет граничной точки многоугольника – в нашем случае это точка – (10 ; 14). В этой точке целевая функция будет достигать максимума.
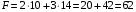
Решим эту задачу симплекс-методом. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам, введя дополнительные переменные .
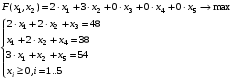
Составляем симплекс-таблицу:
Базис
Cб
В
2
3
0
0
0
А1
А2
А3
А4
А5
А3
0
48
2
2
1
0
0
А4
0
38
1
2
0
1
0
А5
0
54
3
1
0
0
1
Fi - Ci
0
-2
-3
0
0
0
В графе Базис записываются вектора переменных, принимаемые за базисные. На первом этапе это – А3, А4, А5. Базисными будут переменные, каждая из которых входит только в одно уравнение системы, и нет такого уравнения, в которое не входила бы хотя бы одна из базисных переменных.
В следующий столбец записываются коэффициенты целевой функции, соответствующие каждой переменной. Столбец В – столбец свободных членов. Далее идут столбцы коэффициентов Аi при i –й переменной.
Под столбцом свободных членов записывается начальная оценка
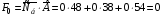
Остальные оценки записываются под столбцами соответствующих векторов .
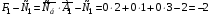
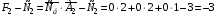
Преобразуем симплекс-таблицу следующим образом:
Шаг 1: Проверяется критерий оптимальности, суть которого состоит в том, что все оценки должны быть неотрицательны. В нашем случае этот критерий не выполнен, поэтому переходим ко второму шагу.
Шаг 2: Для отрицательных оценок вычисляются величины:
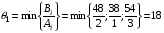
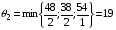
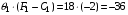
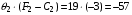
Из этих элементов выбирается тот, для которого вычисленное произведение минимально, в нашем случае -57 минимально, поэтому в качестве разрешающего элемента выбирается второй элемент второго столбца – 2 (выделен в таблице).
Шаг 3: Вторая строка таблицы делится на 2
От элементов строки 1 отнимает соответствующие элементы строки 2, умноженные на 2.
От элементов строки 3 отнимает соответствующие элементы строки 2.
От элементов строки 4 отнимает соответствующие элементы строки 2, умноженные на -3.
Базис
Cб
В
2
3
0
0
0
А1
А2
А3
А4
А5
А3
0
10
1
0
1
-
0
А5
0
19
0,5
1
0
0,5
0
А2
3
35
2,5
0
0
-0,5
1
Fi - Ci
57
-0,5
0
0
1,5
0
Таким образом, новыми базисными переменными становятся А3, А5, А2.
Возвращаемся к шагу 1 и повторяем весь процесс.
Проверяется критерий оптимальности. Отрицательная оценка только одна – в столбце А1.
Вычисляем:
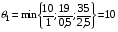
Разрешающим элементом будет первый элемент первого столбца – 1.
Новыми базисными переменными становятся A5, A2, A1
От элементов строки 2 отнимает соответствующие элементы строки 1, умноженные на 0,5.
От элементов строки 3 отнимает соответствующие элементы строки 1, умноженные на 2,5.
От элементов строки 4 отнимает соответствующие элементы строки 1, умноженные на -0,5.
Базис
Cб
В
2
3
0
0
0
А1
А2
А3
А4
А5
А5
0
10
1
0
1
-1
0
А2
3
14
0
1
-0,5
1
0
А1
2
10
0
0
-2,5
2
1
Fi - Ci
62
0
0
1,5
1
0,5
Отрицательных оценок нет, то есть критерий оптимальности выполнен.
Таким образом, получается искомое значение целевой функции
F(10; 14; 0; 0; 10) = 62, т.е. возвращаясь к системе неравенств, получаем:
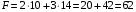
Ответы, полученные различными методами, совпадают.
Ответ: хопт = ( 10 , 14) Значение функции : F = 62
Задача 2
Имеются три пункта отправления А1,А2,А3 однородного груза и пять пунктов В1, В2, В3, В4, В5 его назначения. На пунктах А1,А2,А3 находится груз в количествах 50, 30, 70 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно 20, 30, 50, 30, 20 тонн груза. Расстояния в сотнях километрах между пунктами отправления и назначения приведены в матрице D:
Пункты
отправления
Пункты назначения
В1
В2
В3
В4
В5
А1
9
5
1
1
9
А2
7
1
4
9
4
А3
5
3
4
9
9
Найти такой план перевозок, при котором общие затраты на перевозку грузов будут минимальными.
Указания: 1) считать стоимость перевозок пропорциональной количеству груза и расстоянию, на которое этот груз перевозится, т.е. для решения задачи достаточно минимизировать общий объем плана, выраженный в тонно-километрах;
2) для решения задачи использовать методы северо-западного угла и потенциалов.
Решение.
Составим математическую модель задачи:
Обозначим 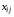 - количество груза, перевезенного из пункта отправления i в пункт назначения j.
- количество груза, перевезенного из пункта отправления i в пункт назначения j.
Получим следующие ограничения (т.к. весь груз должен быть вывезен, и все потребности удовлетворены полностью):
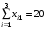
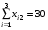
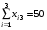
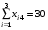
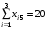
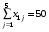
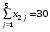
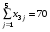
При этом должна быть минимизирована целевая функция
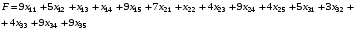
Построим опорный план методом северо-западного угла:
Пункты
отправления
Пункты назначения
Запасы
В1
В2
В3
В4
В5
А1
9
20
5
30
1
1
9
50
А2
7
1
4
30
9
4
30
А3
5
3
4
20
9
30
9
20
70
Потребности
20
30
50
30
20
150
Принцип заполнения таблицы состоит в том, что, начиная с крайней левой верхней ячейки (принцип северо-западного угла), количество грузов вписывается в таблицу так, чтобы потребности полностью удовлетворялись или груз полностью вывозился.
Построим систему потенциалов. Ui - потенциалы, соответствующие поставщикам, Vi- потенциалы, соответствующие потребителям.
Полагаем U1 =0, а далее Ui + Vi = dij для занятых клеток таблицы.
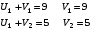
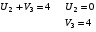
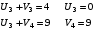
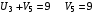
Пункты
отправления
Пункты назначения
Запасы
В1
В2
В3
В4
В5
V1 =9
V2 =5
V3 =4
V4 =9
V5 =9
А1
U1 =0
9
20
5
30
1
1
9
50
А2
U2 =0
7
1
4
30
9
4
30
А3
U3 =0
5
3
4
20
9
30
9
20
70
Потребности
20
30
50
30
20
150
Проверим критерий оптимальности : 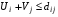 для свободных клеток.
для свободных клеток.
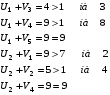
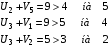
Из тех условий, где критерий не выполняется, выбираем то условие, где разница максимальна. Это – ячейка (1 , 4). Перебросим в ячейку (1 , 4) 20 единиц груза из ячейки (1 , 1).
Пункты
отправления
Пункты назначения
Запасы
В1
В2
В3
В4
В5
V1 =9
V2 =5
V3 =4
V4 =9
V5 =9
А1
U1 =0
9
5
30
1
1
20
9
50
А2
U2 =0
7
1
4
30
9
4
30
А3
U3 =0
5
20
3
4
20
9
10
9
20
70
Потребности
20
30
50
30
20
150
Чтобы компенсировать недостаток в третьей строке, перебросим те же 20 единиц груза из ячейки (3 , 4) в ячейку (3 , 1).
Получили новую таблицу, для которой повторяем расчет потенциалов:
Полагаем U1 =0, а далее Ui + Vi = dij для занятых клеток таблицы.
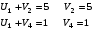
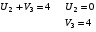
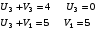
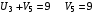
Пункты
отправления
Пункты назначения
Запасы
В1
В2
В3
В4
В5
V1 =5
V2 =5
V3 =4
V4 =1
V5 =9
А1
U1 =0
9
5
30
1
1
20
9
50
А2
U2 =0
7
1
4
30
9
4
30
А3
U3 =0
5
20
3
4
20
9
10
9
20
70
Потребности
20
30
50
30
20
150
Проверим критерий оптимальности : 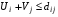 для свободных клеток.
для свободных клеток.
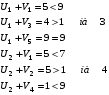
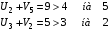
Из тех условий, где критерий не выполняется, выбираем то условие, где разница максимальна. Это – ячейка (2 , 5). Перебросим в ячейку (2 ,5) 20 единиц груза из ячейки (1 , 2).
Пункты
отправления
Пункты назначения
Запасы
В1
В2
В3
В4
В5
V1 =5
V2 =5
V3 =4
V4 =1
V5 =9
А1
U1 =0
9
5
10
1
20
1
20
9
50
А2
U2 =0
7
1
4
10
9
4
20
30
А3
U3 =0
5
20
3
20
4
20
9
10
9
70
Потребности
20
30
50
30
20
150
Получили новую таблицу, для которой повторяем расчет потенциалов:
Полагаем U1 =0, а далее Ui + Vi = dij для занятых клеток таблицы.
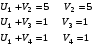
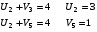
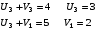
Пункты
отправления
Пункты назначения
Запасы
В1
В2
В3
В4
В5
V1 =2
V2 =5
V3 =1
V4 =1
V5 =1
А1
U1 =0
9
5
10
1
20
1
20
9
50
А2
U2 =3
7
1
4
10
9
4
20
30
А3
U3 =3
5
20
3
20
4
20
9
10
9
70
Потребности
20
30
50
30
20
150
Проверим критерий оптимальности : 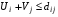 для свободных клеток.
для свободных клеток.
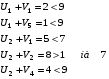
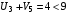
Из тех условий, где критерий не выполняется, выбираем то условие, где разница максимальна. Это – ячейка (2 , 2). Перебросим в ячейку (2 ,2) 10 единиц груза из ячейки (1 , 2).
Пункты
отправления
Пункты назначения
Запасы
В1
В2
В3
В4
В5
V1 =2
V2 =5
V3 =1
V4 =1
V5 =1
А1
U1 =0
9
5
1
20
1
30
9
50
А2
U2 =3
7
1
10
4
9
4
20
30
А3
U3 =3
5
20
3
20
4
30
9
9
70
Потребности
20
30
50
30
20
150
Получили новую таблицу, для которой повторяем расчет потенциалов:
Полагаем U1 =0, а далее Ui + Vi = dij для занятых клеток таблицы.
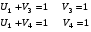
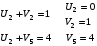
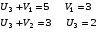
Пункты
отправления
Пункты назначения
Запасы
В1
В2
В3
В4
В5
V1 =3
V2 =1
V3 =1
V4 =1
V5 =4
А1
U1 =0
9
5
1
20
1
30
9
50
А2
U2 =0
7
1
10
4
9
4
20
30
А3
U3 =2
5
20
3
20
4
30
9
9
70
Потребности
20
30
50
30
20
150
Проверим критерий оптимальности : 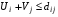 для свободных клеток.
для свободных клеток.
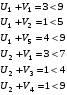
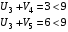
Критерий выполнен, значит, полученное решение оптимально.
Найдем минимальную стоимость перевозок.
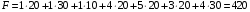
Ответ: 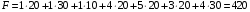
Задача 3
Дана задача выпуклого программирования. Требуется:
1) найти решение графическим методом
2) написать функцию Лагранжа данной задачи и найти ее седловую точку, используя решение задачи, полученное графически.
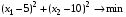
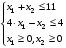
Решение.
Графическое решение задачи следующее:
Система неравенств определяет область, ограниченную двумя прямыми и координатными осями. График целевой функции представляет собой окружность переменного радиуса с центром в точке (5, 10). Значение целевой функции графически представляет собой квадрат радиуса этой окружности. Минимальным радиусом, удовлетворяющим системе ограничений, будет такой радиус, который обеспечивает касание окружности с границей области так, как это показано на рисунке.
Искомая точка определяется как решение системы уравнений
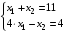
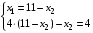
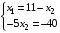
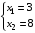
Получили точку (3 , 8), значение целевой функции в этой точке равно 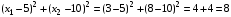
Запишем задачу в традиционном виде:
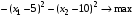
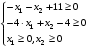
Функция 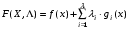 называется функцией Лагранжа, а переменные
называется функцией Лагранжа, а переменные 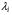 - коэффициентами Лагранжа.
- коэффициентами Лагранжа.
Точка 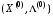 называется седловой точкой функции Лагранжа, если для любых
называется седловой точкой функции Лагранжа, если для любых 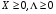 выполняются неравенства:
выполняются неравенства:
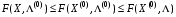
Если функции f, g дифференцируемы, то условия определяющие седловую точку (условия Куна-Таккера):
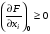
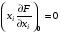
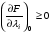
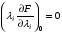
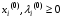
В данном случае получаем:
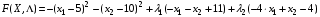
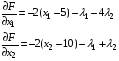
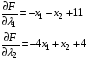
Подставим в эти выражения значения:
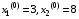
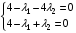
Получаем
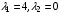
Седловая точка функции Лагранжа: 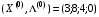
Проверим условие cедловой точки:
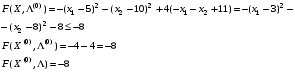
Условия выполнены, седловая точка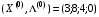 .
.
Ответ: 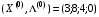
Задача 4
Для двух предприятий выделено 900 единиц денежных средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим, если известно, что доход от х единиц, вложенных в первое предприятие равен 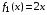 , а доход от у единиц, вложенных во второе предприятие равен
, а доход от у единиц, вложенных во второе предприятие равен 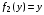 . Остаток средств к концу года составляет
. Остаток средств к концу года составляет 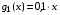 - для первого предприятия,
- для первого предприятия, 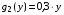 - для второго предприятия. Решить задачу методом динамического программирования.
- для второго предприятия. Решить задачу методом динамического программирования.
Решение.
Процесс распределения средств разобьем на 4 этапа – по соответствующим годам.
Обозначим 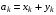 - средства, которые распределяются на k–ом шаге как сумма средств по предприятиям.
- средства, которые распределяются на k–ом шаге как сумма средств по предприятиям.
Суммарный доход от обоих предприятий на k–ом шаге:
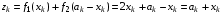
Остаток средств от обоих предприятий на k–ом шаге:
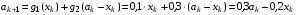
Обозначим 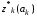 - максимальный доход, полученный от распределения средств между двумя предприятиями с k-го шага до конца рассматриваемого периода.
- максимальный доход, полученный от распределения средств между двумя предприятиями с k-го шага до конца рассматриваемого периода.
Рекуррентные соотношения Беллмана для этих функций
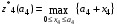
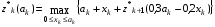
Проведем оптимизацию, начиная с четвертого шага:
4-й шаг.
Оптимальный доход равен:
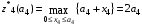 , т.к. линейная возрастающая функция достигает максимума в конце рассматриваемого промежутка, т.е. при
, т.к. линейная возрастающая функция достигает максимума в конце рассматриваемого промежутка, т.е. при 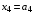 .
.
3-й шаг.
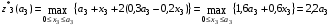
т.к. линейная возрастающая функция достигает максимума в конце рассматриваемого промежутка, т.е. при 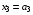 .
.
2-й шаг.
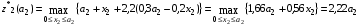 т.к. линейная возрастающая функция достигает максимума в конце рассматриваемого промежутка, т.е. при
т.к. линейная возрастающая функция достигает максимума в конце рассматриваемого промежутка, т.е. при 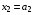 .
.
1-й шаг.
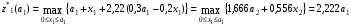
т.к. линейная возрастающая функция достигает максимума в конце рассматриваемого промежутка, т.е. при 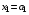 .
.
Результаты оптимизации:
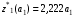
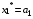
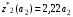
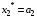
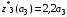
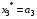
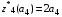
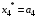
Определим количественное распределение средств по годам:
Так как 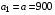 ,
, 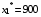 , получаем
, получаем
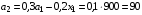
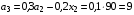
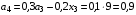
Представим распределение средств в виде таблицы:
предприятие
год
1
2
3
4
1
900
90
9
0,9
2
0
0
0
0
При таком распределении средств за 4 года будет получен доход, равный 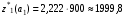
Ответ: 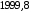

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ