Математика
Канашский филиал
КОНТРОЛЬНАЯ РАБОТА № 1
По математике
Вариант 3
Студента 1 курса экономического факультета
Шифр: 04653033 Учебная группа: 53-06
Работа выслана в Чувашский госуниверситет
«____» ____________2006 г.
Передана на кафедру «Экономики и управления»
Оценка___________ «___» _____________2006г.
Преподаватель: Бычков Владимир Порфирьевич
Возвращена в деканат______________________
Математика
Вариант 3
Даны вершины А(х1;у1) ,В(х2;у2), С(х3;у3) треугольника. Требуется найти: 1)длину стороны ВС; 2)площадь треугольника; 3)уравнение стороны ВС; 4)уравнение высоты проведенной из вершины А; 5)длину высоты проведенной из вершины А; 6)уравнение биссектрисы внутреннего угла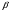 ;
;
7)угол 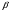 в радианах с точностью до 0,01; 8)систему неравенств определяющих множество точек треугольника. Сделать чертеж.
в радианах с точностью до 0,01; 8)систему неравенств определяющих множество точек треугольника. Сделать чертеж.
вариант 3: А(5;-1), В(1;-4), С(-4;8).
Решение:
1)Длина стороны ВС:
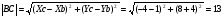
 ;
;
2)Длина стороны АВ:
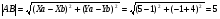 ;
;
Скалярное произведение векторов 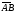 и
и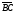
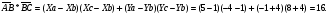
Угол 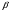 :
:
 cos
cos 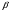 =
=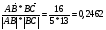 ;
; 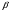 =arcos 0,2462=75,75
=arcos 0,2462=75,75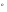 ;
;
3) Уравнение стороны ВС:
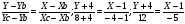
 ;
; 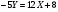 ;
; 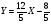 ;
; 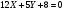 ;
; 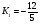 ;
;
4) Уравнение высоты, проведенной из вершины А:
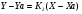 ;
; 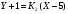 ;
;
Условие перпендикулярности двух прямых:
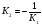 ;
; 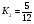 ;
;
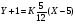 ;
; 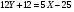 ;
; 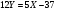 ;
; 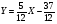 ;
;
5) Длина высоты, проведенной из вершины А:
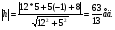
6) 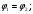
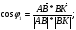

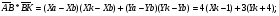
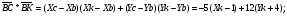
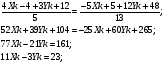
Уравнение прямой АС:
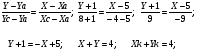
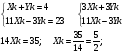
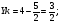
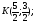
Уравнение биссектрисы внутреннего угла 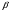 :
:
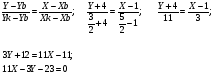
7) Угол 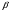 в радианах с точностью до 0,01:
в радианах с точностью до 0,01:
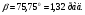
8) Уравнение стороны ВС:
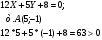
Уравнение стороны АС:
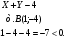
Уравнение стороны АВ:
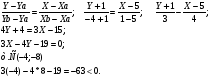
Система неравенств, определяющих множество внутренних точек треугольника.
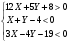
X
Y
A (5;-1)
B (1;-4)
C (-4;8)
 Задание 13.
Задание 13.
Составить уравнение прямой, проходящей через точку А(4;1) на расстоянии 4 единиц от точки В(-4;0).
Решение:
Уравнение пучка прямых, проходящих через точку А:
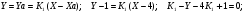
По условию задачи 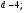

Искомые прямые:
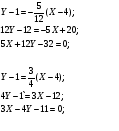
Задание 23.
Составить уравнение линии, расстояние каждой точки которой от точки F(8;0) вдвое больше, чем от прямой Х-2=0. Сделать чертеж.
Решение:
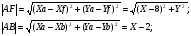
По условию задачи: 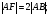
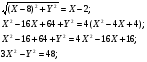
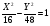 - уравнение гиперболы с центром в точке
- уравнение гиперболы с центром в точке 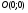 и полуосями
и полуосями 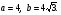

A(x;y)
F(8;0)
X
Y
4 6 8
2
-2
-4
-6
Задание 33.
Составить уравнение параболы и ее директрисы, если известно что парабола проходит через точки пересечения прямой 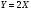 с окружностью
с окружностью 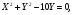 и ось
и ось 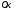 является осью симметрии параболы. Сделать чертеж.
является осью симметрии параболы. Сделать чертеж.
Решение.
Рассмотрим уравнение окружности:
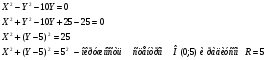
Найдем точки пересечения окружности и прямой.
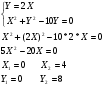
Координаты точек пересечения окружности и прямой 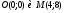 т.к. парабола симметрична относительно ОХ, то уравнение имеет вид
т.к. парабола симметрична относительно ОХ, то уравнение имеет вид 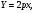 учитывая что
учитывая что 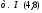 найдем параметр p
найдем параметр p
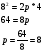
Таким образом, уравнение параболы 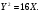
Уравнение директрисы параболы: 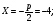
1 3 5 7 9
8
5
2 4 6 8 10
Y
X
M
Y=2x
X=-4
-4
Задание 43.
Дано уравнение параболы f(x;y)=0. Сделать параллельный перенос осей координат так, чтобы в новой системе координат XO1Y уравнение параболы приняло вид X2=aY или Y2=aX. Построить обе системы координат и параболу.
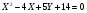
Решение:
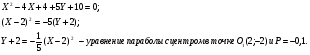
O1
O
y Y
x
X
Задание 53
Даны вершины А1(Х1;Y1;Z1),. А2(Х2;Y2;Z2), А3(Х3;Y3;Z3), А4(Х4;Y4;Z4)
пирамиды. Требуется найти: 1) длину ребра А1А2; 2)Угол между ребрами А1А2 и А1А4; 3)угол между ребром А1А2 и гранью А1А2 А3; 4) площадь грани А1А2 А3; 5) объем пирамиды; 6) уравнение высоты, опущенной из вершины А4 на грань А1А2 А3; 7) уравнение плоскости, проходящей через высоту пирамиды, опущенной из вершины А4 на грань А1А2 А3, и вершину А1 пирамиды.
A1 (3;5;4), А2(5;8;3), А3(1;9;9), A4(6;4;8);
Решение:
1) 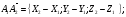
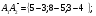
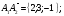
Длина ребра А1А2;

2) 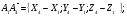
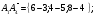
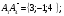
Длина ребра А1А4;
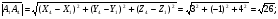
Скалярное произведение векторов А1А2 и А1А4:

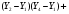
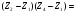
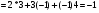
Угол между ребрами А1А2 и А1А4:
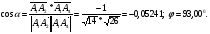
3) Уравнение грани А1А2 А3:
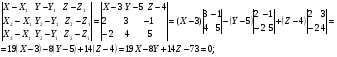
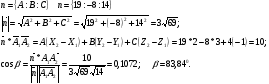
Угол между ребром А1А2 и гранью А1А2 А3:
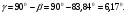
4)Площадь грани А1А2А3:
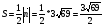 кв. ед.
кв. ед.
5) Объем пирамиды:
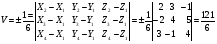 куб. ед.
куб. ед.
6) уравнение высоты, опущенной из вершины А4 на грань А1А2 А3:
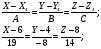
7) Уравнение плоскости, проходящей через высоту пирамиды, опущенной из вершины А4 на грань А1А2 А3, и вершину А1 пирамиды.
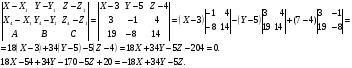
Задание 63.
Определить вид поверхности, заданной уравнением f(x;y;z)=0, и показать её расположение относительно системы координат.
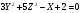
Решение:
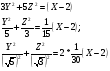
Эллиптический параболоид с вершиной О(z;o;o), направленный вдоль оси ОХ, и имеющий полуоси на оси 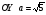 по оси
по оси 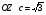
2
Y
Z
X
0
1
Задание 73.
Применяя метод исключения неизвестных, решить систему уравнений.
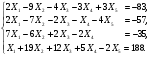
Решение:
2
-9
-4
-3
3
-83
= >
= >
0
-47
-28
-13
7
-459
2
-7
-2
-1
-4
-57
0
-45
-26
-11
0
-433
7
-6
2
-2
0
-35
0
-139
-82
-37
-14
-1351
1
19
12
5
-2
188
1
19
12
5
-2
188
0
-47/7
-4
-13/7
1
-459/7
0
68/77
30/77
0
1
980/77
0
-45
-26
-11
0
-433
0
45/11
26/11
1
0
433/11
0
-233
-138
-63
0
-2269
0
272/11
120/11
0
0
2320/11
1
39/7
4
3/7
0
398/7
1
94/77
-190/77
0
0
481/77
0
0
0
0
1
-2900/77
0
-19/15
0
1
0
-2583/11
0
13,6
1
0
0
116
1
1574/231
0
0
0
22521/77
Общее решение системы:
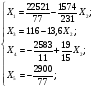
Задание 83.
Даны векторы 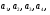 и
и 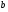 . Показать, что векторы
. Показать, что векторы 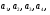 образуют базис четырехмерного пространства, и найти координаты вектора
образуют базис четырехмерного пространства, и найти координаты вектора 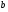 в этом базисе.
в этом базисе.
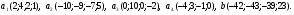
Решение:
Составим определитель из координат векторов 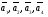 и вычислим его:
и вычислим его:
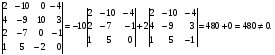
Так как 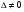 ,то векторы
,то векторы 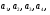 составляют базис. Найдем координаты вектора
составляют базис. Найдем координаты вектора 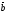 в этом базисе:
в этом базисе:
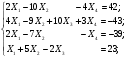
2
-10
0
-4
-42
= >
0
-20
4
-4
-88
= >
0
48
-12
252
4
-9
10
3
-43
0
-29
18
3
-135
0
-80
30
-350
2
-7
0
-1
-39
0
-17
4
-1
-85
0
17
-4
85
1
5
-2
0
23
1
5
-2
0
23
1
5
-2
23
0
-4
1
0
-21
= >
0
0
1
0
3
0
40
0
0
240
0
1
0
0
6
0
1
0
1
1
0
0
0
1
-5
1
-3
0
0
-19
1
0
0
0
-1
Итак 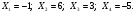
Проверка:
2(-1)-10*6 -4(-5)=-42; -42=-42;
4(-1)-9*6+10*3+3(-5)=-43; -43=-43;
2(-1)-7*6- -(-5)=-39; -39=-39;
-1+5*6-2*3 =23; 23=23.
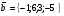 или
или 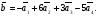
Задание 93.
Дана матрица А . Требуется найти: 1) матрицу, обратную матрице А;
2) собственные значения и собственные векторы матрицы А.
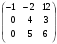
Решение:
-1
-2
12
1
0
0
1
2
-12
-1
0
0
0
4
3
0
1
0
0
4
3
0
1
0
0
5
6
0
0
1
0
5
6
0
0
1
1
0
-13,5
-1
-0,5
0
1
0
0
-1
-8
6
0
1
0,75
0
0,25
0
0
1
0
0
6/9
-3/9
0
0
2,29
0
-1,25
1
0
0
1
0
-5/9
4/9
Обратная матрица:
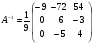
Корни характеристического уравнения:
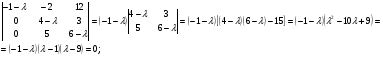
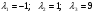 - собственные значения матрицы А .
- собственные значения матрицы А .
При 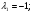

Собственный вектор:
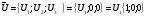
Задание 103.
Построить график функции y=f(x) деформацией и сдвигом графика функции y=sin x.
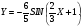
Решение:
-2П -3/2П -П -П/2 П/2 П 3/2П 2П
Y=-6/5sin(2/3x+1)
-6/5
X
-6/5
Y=sin(2/3x+1)
1
X
-1
Y=sin(2/3x)
1
X
-1
Y=sin x
1
X
-1
Y1
Сжатие вдоль оси ОХ в 2/3 раза
Сдвиг влево на 1 вдоль оси ОХ
Растягивание в 6/5 раза и
переворот вдоль OY
Задание 113.
Найти указанные пределы (не пользуясь правилом Лопиталя).
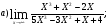
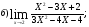
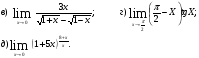
Решение:
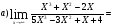
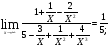
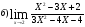
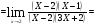
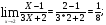
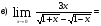
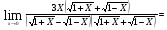
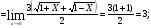
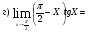
Подстановка: 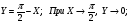

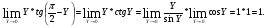
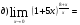
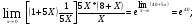
Задание 123.
Дана функция y=f(x) и три значения аргумента x1,x2,x3. Установить, является ли эта данная функция непрерывной или разрывной для каждого из данных значений Х. Построить (приближенно) график функции в окрестностях каждой из данных точек.
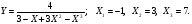
Решение:
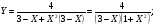
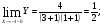
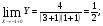
Так как 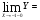
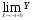 ,то функция в точке Х1=-1 непрерывна.
,то функция в точке Х1=-1 непрерывна.
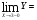
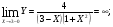
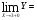
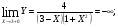
Так как 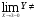
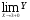 ,то функция в точке х=3 разрывная.
,то функция в точке х=3 разрывная.
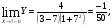
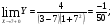
Так как 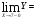
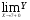 ,то функция в точке х=7 непрерывна.
,то функция в точке х=7 непрерывна.
Y=3
Y
X
-1 0 7
Задание 133.
Функция y=f(x) задана различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Построить график.
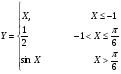
Решение:
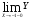
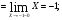
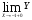
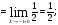
Так как 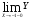
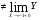 , то функция в точке х=-1 разрывна.
, то функция в точке х=-1 разрывна.
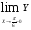
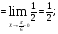
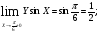
Так как 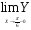
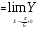 , то функция в точке
, то функция в точке 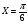 непрерывна.
непрерывна.
Y
-1 П/6 X
Задание 143.
Найти производные 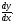
 a)
a) 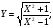 б)
б) 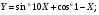 в)
в) 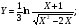
г) 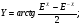 д)
д) 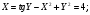
Решение.
а) 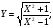
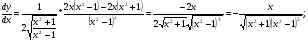
б) 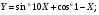
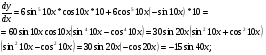
в) 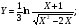
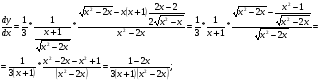
г) 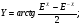
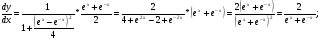
д) 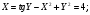
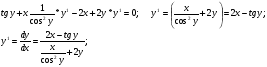
Задание 153.
Найти 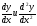 для функции, заданной параметрическим.
для функции, заданной параметрическим.
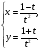
Решение.
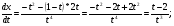
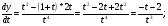
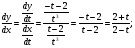
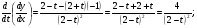
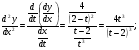
Задание 163.
На линии 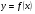 найти точку, в которой касательная к этой линии параллельна прямой
найти точку, в которой касательная к этой линии параллельна прямой 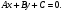
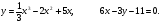
Решение.
Угловой коэффициент прямой:
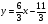 или
или 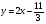
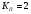

Угловой коэффициент касательной к линии:
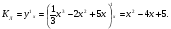
Так как касательная к линии и прямая параллельны, то 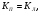
тогда:
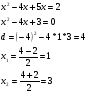
Таким образом получаются две точки:
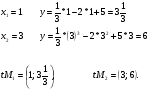
Задание 173.
Какова должна быть высота равнобедренного треугольника, вписанного в окружность диаметра d, чтобы площадь треугольника была наибольшей?
Решение.
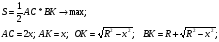
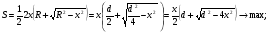
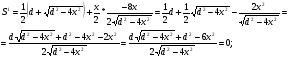
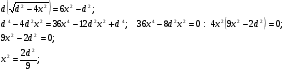
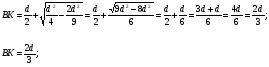
B
R
O
R
A K C
Задание 183.
Исследовать методами дифференциального исчисления и построить график.
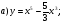

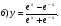
Решение.
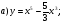
1. область определения функции: 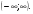
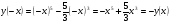

так как 
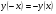 то функция нечетная.
то функция нечетная.
2. Точки пересечения с осями координат:
При 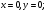 при
при 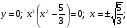

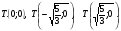
3. Область возрастания (убывания) функции, точки экстремумов:
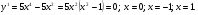
При 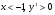 функция возрастает.
функция возрастает.
При 
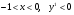 функция убывает.
функция убывает.
При  функция убывает.
функция убывает.
При 
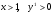 функция возрастает
функция возрастает
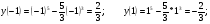
Точка 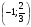 точка максимума.
точка максимума.
Точка 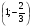 точка минимума.
точка минимума.
4. Область выпуклости (вогнутости) функции, точки перегибов.
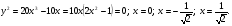
При 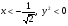 функция выпукла;
функция выпукла;
При 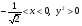 функция вогнута;
функция вогнута;
При 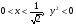 функция выпукла;
функция выпукла;
При 
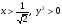 функция вогнута.
функция вогнута.
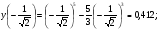
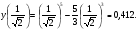
Точки 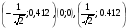 - точки перегибов.
- точки перегибов.
5. Асимптот нет
Y
X

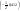
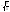
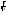
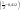
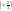
0

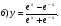
1. область определения функции: 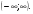
2. точки пересечения с осями координат:
При 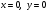
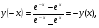 так как
так как 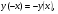 то функция нечетная.
то функция нечетная.
3. области возрастания (убывания) функции; точки экстремумов.

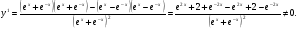
Точек экстремумов нет.
Так как 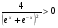 то функция возрастает.
то функция возрастает.
4. область выпуклости (вогнутости) функции; точки экстремумов.
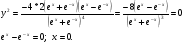
При 
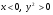 функция вогнута;
функция вогнута;
При 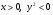 функция выпукла;
функция выпукла;
Точка (0;0) точка перегиба.
5. асимптоты.
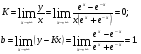
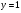 асимптота.
асимптота.

0
X
Y
1
-1
Задание 193.
Определить количество действительных корней уравнения 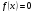 ;
;
отделить эти корни и, применяя метод хорд и касательных, найти их приближенные значения с точностью до 0,001.
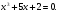
Решение.
Исследуем график функции.
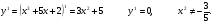
Количество корней К=1.
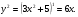
Таким образом, функция принимает значения на отрезке 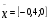 ,в качестве начального приближения возьмем
,в качестве начального приближения возьмем 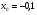
метод касательных:
составим таблицу:
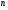
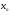
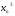
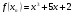

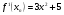
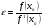
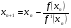
1
2
3
-0,1
-0,398
-0,388
-0,001
-0,063
-0,586
1,499
-0,053
-0,0001
5,03
5,475
5,452
0,298
-0,0097
-0,00002
-0/3980
-0,3883
-0,3882
Искомый корень х=-03882
Задание 203.
Найти частные производные функции 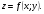

Решение.
Частные производные:
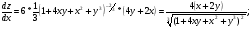
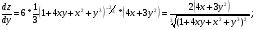
Задание 213.
Дана функция 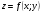 и две точки
и две точки 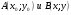 . Требуется:
. Требуется:
1) вычислить приближенное значение функции у точке В, исходя из значения в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 2) вычислить точное значение функции в точке В и оценить в процентах относительную погрешность, возникающую при замене приращения функции дифференциалом.
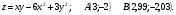
Решение.
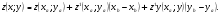
Вычислим частные производные в точке А.

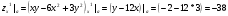
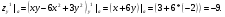
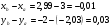
Приближенное значение:
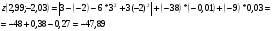
Вычислим точки значения функции:

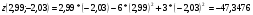
Относительная погрешность вычисления:

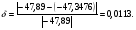
Задание 223.
Даны функция  точка
точка 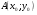 и вектор а. Требуется найти:
и вектор а. Требуется найти:
1) grad z в точке А; 2)производную по направлению вектора в точке А.

Решение.
1) вектором градиентом функции двух переменных 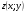 является вектор:
является вектор:

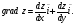
Найдем частные производные в точке А:
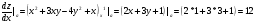
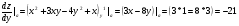
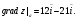
2) производная по направлению вектора  вычисляется по формуле.
вычисляется по формуле.
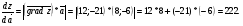
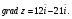
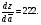
Задание 233.
Найти наименьшее и наибольшее значение функции  в замкнутой области, ограниченной заданными линиями.
в замкнутой области, ограниченной заданными линиями.
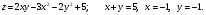
Решение.
Частные производные:

На прямой АВ: 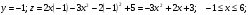 \
\

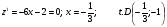
На прямой АС: 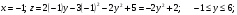
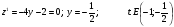
На прямой ВС: 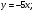
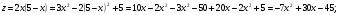

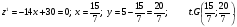

Z наибольшее =5; z наименьшее =-117.
О(0;0)
Y
X

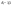
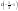
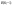
Использованная литература:
1 Ткачук В.В. Математика абитуриенту:-М:МЦНМО,2002 г.
2 Сканави М.И. 2500 задач по математике для поступающих в вузы:
-М: Оникс 21 век, 2005 г.
3 Мельников И.И. Как решать задачи по математике на вступительных экзаменах. 3-е издание, переработанное: учебник/ И.И Мельников, И.Сергеев.-М:УНЦДО, 2004 г.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ