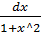
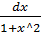
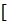
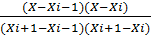
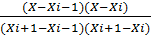
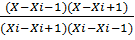
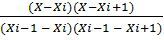
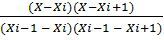
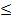
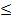
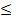
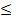
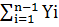
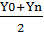
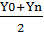
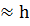
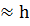
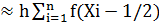
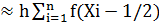
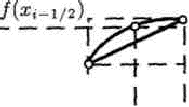
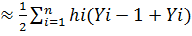
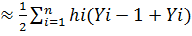
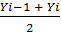
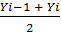
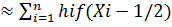
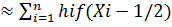
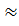
Методы прямоугольников и трапеций. Простейшим методом численного интегрирования является метод прямоугольников. Он непосредственно использует замену определенного интеграла интегральной суммой (3.20). В качестве точек ξ_i могут выбираться левые (ξ = x_i-1) или правые (ξ_i = x_i) границы элементарных отрезков. Обозначая f{x_i) = y_i, ∆x_i = h_i, получаем следующие формулы метода прямоугольников соответственно для этих двух случаев:

∫ f(x) dx h₁y₀ + h₂y₁ + ... + h_ny_n-1 (3.24)

∫ f(x) dx h₁y₁ + h₂y₂ + ... + h_ny_n (3.25)

Широко распространенным и более точным является вид формулы прямоугольников, использующий значения функции в средних точках элементарных отрезков (в полуцелых узлах):

∫ f{x)dx, (3.26)

X_i-1/2 = (x_i-1 + x_i)/2 = x_i-1 + h_i/2, i = 1,2,... ,n.

В дальнейшем под методом прямоугольников будем понимать последний алгоритм (он еще называется методом средних).

В рассмотренных методах прямоугольников используется кусочно постоянная интерполяция: на каждом элементарном отрезке функция f(x) приближается функцией, принимающей постоянные значения (константой). При этом площадь всей фигуры (криволинейной трапеции) приближенно складывается из площадей элементарных прямоугольников. На рис. 3.2 верхняя, средняя и нижняя горизонтальные штриховые линии относятся к элементарным прямоугольникам, которые соответствуют формулам (3.25), (3.26) и (3.24).

Метод трапеций использует линейную интерполяцию, т. е. график функции у = f(x) представляется в виде ломаной, соединяющей точки (x_i, y_i). В этом случае площадь всей фигуры приближенно складывается из площадей элементарных прямолинейных трапеций (рис. 3.2). Площадь каждой такой трапеции равна произведению полусуммы оснований на высоту:

σ_i = h_i , i=1,2,...,n.

Складывая все эти равенства, получаем формулу трапеций для численного интегрирования:

∫ f{x)dx (3.27)

y (x_i,y_i)

(x_i-1,y_i-1)

y_i-1 y_i

h_iV

x

x_i-1 x_i-1/2 x_i

Рис. З.2. Вычисление σ_i в методах

прямоугольников и трапеций

Важным частным случаем рассмотренных формул является их применение при численном интегрировании с постоянным шагом h_i = h = const (i = 1,2,...,n). Формулы прямоугольников и трапеций в этом случае принимают соответственно вид

∫ f{x)dx, (3.28)

∫ f{x)dx(+). (3.29)

Погрешность численного интегрирования определяется шагом разбиения. Уменьшая этот шаг, можно добиться большей точности. Правда, увеличивать число точек не всегда возможно. Если функция задана в табличном виде, приходится, как правило, ограничиваться данным множеством точек. Повышение точности может быть в этом случае достигнуто за счет повышения степени используемых интерполяционных многочленов. Рассмотрим два таких способа численного интегрирования: использование квадратичной интерполяции (метод Симпсона) и интерполирование с помощью сплайнов.

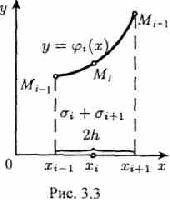
Метод Симпсона. Разобьем отрезок интегрирования [а, b] на четное число п равных частей с шагом h. На каждом отрезке [х₀,х₂], [х₂,х₄],... , [х_i-1,х_i+1], ... , [х_n-2,x_n] подынтегральную функцию f(x) заменим интерполяционным многочленом второй степени:

f(x)φ_i(x) = a_ix²+bⁱx+c_i, x_i-1x x_i+1.

Коэффициенты этих квадратных трехчленов могут быть найдены из условий равенства многочлена в точках х_i, соответствующим табличным данным у_i. В качестве φ_i (х) можно принять интерполяционный многочлен Лагранжа второй степени, проходящий через точки M_i-1(x_i-1,y_i-1), M_i(x_i,y_i), M_i+1(x_i+1, y_i+1):

φ_i(x)= y_i-1+ y_i+ y_i+1.

Сумма элементарных площадей σ_i и σ_i+1 (рис. 3.3) может быть вычислена с помощью определенного интеграла. Учитывая равенства x_i+1 – x_i = x_i - x_i-1 = h, получаем

σ_i + σ_i+1=∫ φ_i(x)dx=1/2h²∫ (x-x_i)(x-x_i+1)y_i-1-2(x-x_i-1)(x-x₊₁)y_i+(x-x_i-1)(x-x_i)y_i+1]dx=

= h/3(y_i-1+4y_i+y_i+1)

Проведя такие вычисления для каждого элементарного отреза [х_i-1,х_i+1], просуммируем полученные выражения:

S = h/3(y₀+4y₁+2y₂+4y₃+2y₄+...+2y_n-2+4y_n-1+y_n).

Данное выражение для S принимается в качестве значения определенного интеграла:

∫f(x)dxh/3[y₀+4(y₁+y₃+...+y_n-1)+2(y₂+y₄+...+y_n-2)+y_n]. (3.30)

Полученное соотношение называется формулой Симпсона или формулой парабол.

Эту формулу можно получить и другими способами, например двукратным применением метода трапеций при разбиениях отрезка [а, b] на части с шагами h и 2h или комбинированием формул прямоугольников и трапеций (см. п. 5).

Иногда формулу Симпсона записывают с применением полуцелых индексов. В этом случае число отрезков разбиения п произвольно (не обязательно четно), и формула Симпсона имеет вид

∫ f(x)dxh/6[y₀+4(y_1/2+y_3/2+...+y_n-1/2)+2(y₁+y₂+...+y_n-1)+y_n]. (3.31)

Легко видеть, что формула (3.31) совпадет с (3.30), если формулу (3.30) применить для числа отрезков разбиения 2п и шага h/2.

Пример. Вычислить по методу Симпсона интеграл I =∫.

Значения функции при п = 10, h = 0.1 приведены в табл. 3.3.

Применяя формулу (3.30), находим

I=0.1/3[y₀+4(y₁+y₃+y₅+y₇+y₉)+2(y₂+y₄+y₆+y₈)+y₁₀]=...=0.785398.

Результат численного интегрирования с использованием метода Симпсона оказался совпадающим с точным значением (шесть значащих цифр).

Один из возможных алгоритмов вычисления определенного интеграла по методу Симпсона представлен на рис. 3.4. В качестве исходных данных задаются границы отрезка интегрирования [а, b], погрешность ε, а также формула для вычисления значений подынтегральной функции у = f(х). Первоначально отрезок [а, b] разбивается на две части с шагом h = (b — а)/2. Вычисляется значение интеграла 1₁. Потом число шагов удваивается, вычисляется значение 1₂ с шагом h/2. Условие окончание счета принимается в виде | I₁ —1₂ | < е. Если это условие не выполнено, происходит новое деление шага пополам и т. д.

Отметим, что представленный на рис. 3.4 алгоритм не является оптимальным: при вычислении каждого приближения I₂ не используются значения функции f(х), уже найденные на предыдущем этапе.

6