Методы решения систем линейных уравнений
Методы решения систем линейных уравнений
1. Решение системы линейных уравнений методом Гаусса
Задачи аппроксимации функции, а также множество других задач прикладной математики м вычислительной физики сводятся к задачам о решении систем линейных уравнений. Самым универсальным методом решения системы линейных уравнений является метод последовательного исключения неизвестных, называемый методом Гаусса.
Для иллюстрации смысла метода Гаусса рассмотрим систему линейных уравнений:
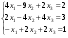 (1)
(1)
Эту систему запишем в матричном виде:
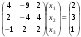 (2)
(2)
Как известно, обе части уравнения можно умножить на ненулевое число, а также можно из одного уравнения вычесть другое. Используя эти свойства, постараемся привести матрицу системы (2) к треугольному виду, т.е. к виду, когда ниже главной диагонали все элементы – нули. Этот этап решения называется прямым ходом.
На первом шаге прямого хода умножим первое уравнение на 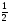 и вычтем из второго, тогда исключится переменная
и вычтем из второго, тогда исключится переменная 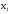 из второго уравнения. Затем, умножим первое уравнение на
из второго уравнения. Затем, умножим первое уравнение на 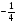 и вычтем из третьего, тогда система (2) преобразуется в систему вида:
и вычтем из третьего, тогда система (2) преобразуется в систему вида:
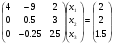 (3)
(3)
На втором шаге прямого хода из третьего уравнения исключаем 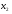 , т.е. из третьего уравнения вычитаем второе, умноженное, на
, т.е. из третьего уравнения вычитаем второе, умноженное, на 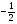 , что приводит систему (3) к треугольному виду (4)
, что приводит систему (3) к треугольному виду (4)
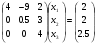 (4)
(4)
Систему (4) переписываем в привычном виде:
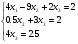 (5)
(5)
Теперь, из системы (5) можем находить решение в обратном порядке, т.е. сначала находим из третьего уравнения 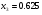 , далее, подставляя во второе уравнение, находим
, далее, подставляя во второе уравнение, находим 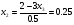 . Подставляя
. Подставляя 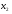 и
и 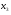 в первое уравнение системы (5), находим
в первое уравнение системы (5), находим 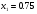 . Нахождение решения
. Нахождение решения 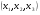 из системы (5) называют обратным ходом.
из системы (5) называют обратным ходом.
Теперь, на основе рассмотренного примера, составим общий алгоритм метода Гаусса для системы:
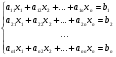 (6)
(6)
Метод Гаусса состоит из двух этапов:
а) прямой ход – когда матрица системы (6) приводится к треугольному виду;
б) обратный ход – когда последовательно вычисляются неизвестные в обратном порядке, т.е. в последовательности: 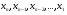 .
.
а) Прямой ход: для приведения системы (6) к треугольному виду, уравнения с ненулевыми коэффициентами при переменной 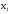 переставляются таким образом, чтобы они были выше, чем уравнения с нулевыми коэффициентами
переставляются таким образом, чтобы они были выше, чем уравнения с нулевыми коэффициентами 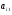 . Далее, вычитаем первое уравнение, помноженное на
. Далее, вычитаем первое уравнение, помноженное на 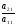 , из второго уравнения, вычитаем первое уравнение, помноженное на
, из второго уравнения, вычитаем первое уравнение, помноженное на 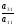 , из третьего уравнения и т.д. В общем, вычитаем первое уравнение, помноженное на
, из третьего уравнения и т.д. В общем, вычитаем первое уравнение, помноженное на 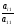 , из
, из 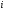 - го уравнения при
- го уравнения при 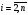 , если
, если 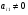 . Вследствие этой процедуры, мы обнулили все коэффициенты при переменной
. Вследствие этой процедуры, мы обнулили все коэффициенты при переменной 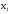 в каждом из уравнений, начиная со второго, т.е. система (6) принимает вид:
в каждом из уравнений, начиная со второго, т.е. система (6) принимает вид:
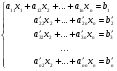 (7)
(7)
Далее, применяем туже самую процедуру, для уравнений системы (7), начиная со второго уравнения, т.е. первое уравнение исключается из «игры». Теперь стараемся обнулить коэффициенты при переменной 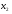 , начиная с третьего уравнения и т.д., пока не приведём систему к треугольному виду. Если
, начиная с третьего уравнения и т.д., пока не приведём систему к треугольному виду. Если 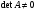 , то система всегда приводима (теоретически) к треугольному виду. Общий алгоритм прямого хода можно представить в виде:
, то система всегда приводима (теоретически) к треугольному виду. Общий алгоритм прямого хода можно представить в виде:
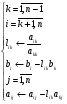 (8)
(8)
б) Обратный ход: Вычисляем неизвестные по формулам:
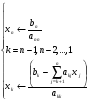 (9)
(9)
Замечание: для вычисления определителя системы можно использовать треугольную форму полученной матрицы, тогда определитель этой матрицы равен произведению диагональных элементов, т.е.
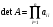 (10)
(10)
2. Метод Гаусса с выбором главного элемента
Метод Гаусса настолько универсален, что для некоторых систем получаются практически «плохие» результаты, поэтому разрабатываются различные хитрые выходы из ситуации. В случае, когда некоторые коэффициенты матрицы системы близки между собой, как известно относительные погрешности сильно возрастают при вычитании, поэтому классический метод Гаусса даёт большие погрешности. Чтобы обойти эту трудность, стараются в прямом ходе Гаусса выбрать то уравнение, у которого коэффициент при 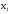 максимален и в качестве основного «игрока» выбирают именно это уравнение, тем самым обходя трудности вычитания близких чисел (если это возможно). Далее, когда нужно обнулить все коэффициенты переменной
максимален и в качестве основного «игрока» выбирают именно это уравнение, тем самым обходя трудности вычитания близких чисел (если это возможно). Далее, когда нужно обнулить все коэффициенты переменной 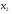 , кроме одного уравнения – этим особым уравнением опять выбирают то уравнение, у которого коэффициент при
, кроме одного уравнения – этим особым уравнением опять выбирают то уравнение, у которого коэффициент при 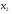 максимальный и т.д., пока не получим треугольную матрицу.
максимальный и т.д., пока не получим треугольную матрицу.
Обратный ход происходит так же, как и в классическом методе Гаусса.
3. Оценка погрешности при решении системы линейных уравнений
Для того, чтобы оценить погрешности вычислений решения системы линейных уравнений, нам нужно ввести понятия соответствующих норм матриц.
Прежде всего, вспомним три наиболее часто употребляемые нормы для вектора 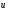 :
:
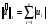 (11)
(11)
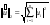 (Евклидова норма) (12)
(Евклидова норма) (12)
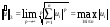 (Чебышевская норма) (13)
(Чебышевская норма) (13)
Для всякой нормы векторов можно ввести соответствующую норму матриц:
 (14)
(14)
которая согласована с нормой векторов в том смысле, что
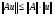 (15)
(15)
Можно показать, что для трёх приведённых выше случаев нормы матрицы 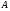 задаются формулами:
задаются формулами:
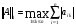 (16)
(16)
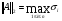 (17)
(17)
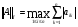 (18)
(18)
Здесь 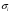 - являются сингулярными числами матрицы
- являются сингулярными числами матрицы 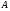 , т.е. это положительные значения квадратных корней
, т.е. это положительные значения квадратных корней 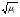 - матрицы
- матрицы 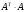 (которая является положительно-определённой матрицей, при
(которая является положительно-определённой матрицей, при 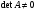 ).
).
Для вещественных симметричных матриц 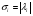 - где
- где 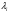 - собственные числа матрицы
- собственные числа матрицы 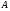 .
.
Абсолютная погрешность решения системы:
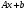 (19)
(19)
где 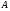 - матрица системы,
- матрица системы, 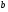 - матрица правых частей, оценивается нормой:
- матрица правых частей, оценивается нормой:
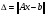 (20)
(20)
Относительная погрешность оценивается по формуле:
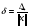 (21)
(21)
где 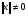 .
.
4. Итерационные методы решения систем линейных уравнений
Рассмотрим систему линейных уравнений, которая плохо решается методами Гаусса. Перепишем систему уравнений в виде:
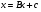 (22)
(22)
где 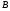 - заданная числовая матрица
- заданная числовая матрица 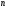 -го порядка,
-го порядка, 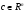 - заданный постоянный вектор.
- заданный постоянный вектор.
4.1 Метод простой итерации Якоби
Этот метод состоит в следующем: выбирается произвольный вектор 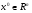 (начальное приближение) и строится итерационная последовательность векторов по формуле:
(начальное приближение) и строится итерационная последовательность векторов по формуле:
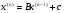 ,
, 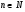 (23)
(23)
Приведём теорему, дающую достаточное условие сходимости метода Якоби.
Теорема. Если 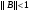 , то система уравнений (22) имеет единственное решение
, то система уравнений (22) имеет единственное решение 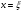 и итерации (23) сходятся к решению.
и итерации (23) сходятся к решению.
Легко заметить, что эта теорема является простым обобщением теоремы о сжатых отображениях изученных нами раньше для одношагового итерационного процесса в общем виде. Все оценки, полученные ранее, переносятся и для системы уравнений, разница лишь в понятиях соответствующих норм. Обобщая метод простой итерации Якоби для случая системы уравнений:
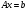 (24)
(24)
Строим алгоритм решения:
а) переписываем уравнение (24) в однородном виде и умножаем на постоянную 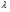 - которую далее найдём из условий сходимости итерационного процесса:
- которую далее найдём из условий сходимости итерационного процесса:
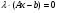 (25)
(25)
б) добавляем 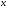 к обеим частям (25) и получаем:
к обеим частям (25) и получаем:
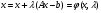 (26)
(26)
в) строим итерационную формулу Якоби:
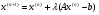 (27)
(27)
где постоянную 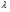 находим из условий сходимости итерационного процесса (27), который в данном случае имеет вид:
находим из условий сходимости итерационного процесса (27), который в данном случае имеет вид:
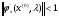 (28)
(28)
где 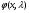 - вектор-функция из (26) или исходя из теоремы о сжатых отображениях
- вектор-функция из (26) или исходя из теоремы о сжатых отображениях 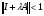 , где
, где 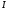 - единичная матрица.
- единичная матрица.
Рассмотрим числовой пример:
Пусть имеем систему уравнений:
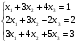
Переписываем систему в виде:
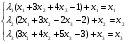
Составляем итерационную формулу:
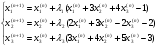
Коэффициент 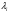 выбираем из условий:
выбираем из условий: 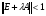 , т.е.
, т.е.
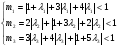
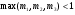 .
.
4.2 Метод Гаусса-Зейделя
Для решения линейной системы уравнений разработано множество итерационных методов. Тем более, что метод простой итерации Якоби сходится медленно. Одним из таких методов является метод Гаусса-Зейделя.
Для иллюстрации метода рассмотрим числовой пример:
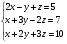 (29)
(29)
Уравнения переписаны таким образом, что на главной диагонали стоят максимальные для каждого уравнения коэффициенты.
Начинаем с приближения 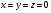 . Используя первое уравнение, находим для
. Используя первое уравнение, находим для 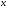 новое значение
новое значение 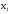 при условии
при условии 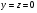 .
.
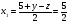 (30)
(30)
Беря это значение 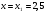 и
и 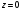 из второго уравнения, находим
из второго уравнения, находим 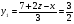 , далее из третьего уравнения находим
, далее из третьего уравнения находим 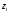 ,
, 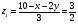 . Эти три величины дают новое приближение и можно повторить цикл с начала, получаем:
. Эти три величины дают новое приближение и можно повторить цикл с начала, получаем: 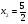 ,
, 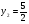 ,
, 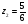 и т.д. Итерации продолжаются до выполнения неравенства
и т.д. Итерации продолжаются до выполнения неравенства 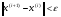 .
.
Общий алгоритм метода Гаусса-Зейделя имеет вид:
Пусть
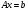 (31)
(31)
где у матрицы 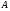 - все диагональные элементы отличны от нуля, т.е.
- все диагональные элементы отличны от нуля, т.е. 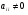 (если
(если 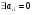 , тогда переставляем строки так, чтобы добиться условия
, тогда переставляем строки так, чтобы добиться условия 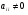 ). Если
). Если 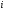 -ое уравнение системы (31) разделить на
-ое уравнение системы (31) разделить на 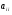 , а затем все неизвестные кроме
, а затем все неизвестные кроме 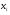 - перенести в правую часть, то мы придём к эквивалентной системе вида:
- перенести в правую часть, то мы придём к эквивалентной системе вида:
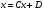 (32)
(32)
где 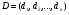 ,
, 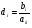 ,
, 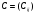
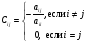 (33)
(33)
Метод Гаусса-Зейделя состоит в том, что итерации производятся по формуле:
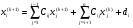 (34)
(34)
где 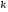 - номер итерации, а
- номер итерации, а 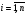 .
.
Замечание: для сходимости метода (34) достаточно выполнения хотя бы одного из условий:
а)
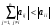 ,
, 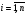 (35)
(35)
б) 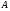 - симметричная и положительно-определённая матрица.
- симметричная и положительно-определённая матрица.
5. Решение системы линейных уравнений методом Ритца
Если 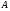 - симметричная и положительно-определённая матрица, то задача решения линейной системы уравнений:
- симметричная и положительно-определённая матрица, то задача решения линейной системы уравнений:
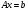 (36)
(36)
эквивалентна задаче нахождения точки минимума функции многих переменных:
 (37)
(37)
где скалярные произведения понимаются в смысле 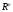 , т.е.
, т.е.
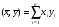 (38)
(38)
Иначе говоря, решение системы линейных уравнений (36) доставляет минимум функции многих переменных:
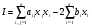 (39)
(39)
И наоборот, точка минимума функции (39) является решением системы линейных уравнений (36).
Таким образом, метод Ритца позволяет решение линейной системы уравнений с симметричной и положительно-определённой матрицей свести к задаче нахождения точки минимума функций многих переменных. А эту задачу мы уже умеем решать.
6. Решение системы линейных уравнений с трехдиаганальной матрицей методом прогонки Томаса
При решении задач конечно-разностными методами или методом конечных элементов, часто решение задачи сводится к решению линейной системы уравнений с трехдиаганальной матрицей коэффициентов, т.е. с матрицей, где все элементы нули, кроме трех диагоналей (в окрестности главной диагонали); рассмотрим систему с трехдиаганальной матрицей:
 (40)
(40)
для решения этой линейной системы уравнений, конечно, можно применять метод Гаусса, но тогда пришлось бы делать много необязательных операций с нулями. Чтобы сэкономить время вычислений и не работать лишний раз с нулями, Томас (1949г.) разработал специальный алгоритм расчета. Рассчитывая по алгоритму Томаса элементы получаемой треугольной матрицы, мы следуем методу Гаусса, с уточнением, что с нулями никаких действий не производим; алгоритм Томаса называют – методом прогонки.
Для решения системы (40) методом прогонки – Томаса действуем следующим образом:
а) прямой ход:
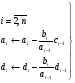 (41)
(41)
Замечание: после проведения прямого хода предполагается, что все 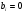 , и
, и 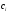 - неизменны (что очевидно).
- неизменны (что очевидно).
б) обратный ход:
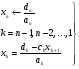 (42)
(42)
Таким образом, для системы линейных уравнений с трехдиаганальной матрицей наиболее экономным является алгоритм прогонки – Томаса, который является «отфильтрованным» методом Гаусса.
Метод минимизации невязки для решения линейной системы уравнений (метод наименьших квадратов).
При проведении экспериментов, часто приходится решать следующую задачу: определить 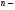 известных
известных 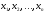 ,которые непосредственно не измеряются, а измеряются величины
,которые непосредственно не измеряются, а измеряются величины 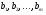 связанные с определяемыми переменными
связанные с определяемыми переменными 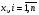 . Измерения не свободны от случайных ошибок, которыми нельзя пренебречь.
. Измерения не свободны от случайных ошибок, которыми нельзя пренебречь.
Число наблюдаемых величин больше числа неизвестных 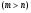 . Пусть известно, что величины
. Пусть известно, что величины 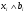 связаны между собой линейной зависимостью:
связаны между собой линейной зависимостью:
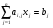 ,
, 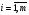 ,
, 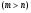 . (43)
. (43)
Коэффициенты 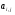 - считаются известными и неотягощенными случайными ошибками. Система (43) называется системой условных уравнений.
- считаются известными и неотягощенными случайными ошибками. Система (43) называется системой условных уравнений.
Если бы все числа 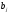 были точными, то неизвестные
были точными, то неизвестные 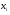 ,
, 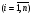 могли бы быть определены из любых
могли бы быть определены из любых 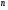 - уравнений системы
- уравнений системы 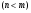 . Но так, как
. Но так, как 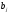 - определены с ошибками, то система условных уравнений несовместна (переопределена, т.к.
- определены с ошибками, то система условных уравнений несовместна (переопределена, т.к. 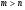 ), существуют «невязки»:
), существуют «невязки»:
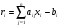 ,
, 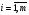
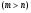 (44)
(44)
задача теперь заключается в том, чтобы найти такие значения 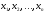 , при которых функция невязки
, при которых функция невязки 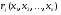 - минимально по некоторой норме, т.е. мы ищем такие
- минимально по некоторой норме, т.е. мы ищем такие 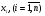 , при которых норма невязки
, при которых норма невязки 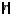 - минимальна.
- минимальна.
В методе наименьших квадратов, в качестве нормы рассматривают дискретную норму Гаусса:
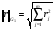 (45)
(45)
Очевидно, что эта норма минимальна тогда, когда минимально подкоренное выражение, т.е. сумма квадратов невязок 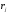 .
.
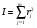 (46)
(46)
Условия существования минимума для функций специального вида 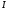 имеют вид:
имеют вид:
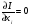 ,
,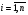 , (47)
, (47)
т.е. задача сводится, как и в общей теории приближений, к решению системы нормальных уравнений.
Для примера рассмотрим 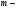 уравнений с тремя неизвестными, система условных уравнений имеет вид:
уравнений с тремя неизвестными, система условных уравнений имеет вид:
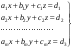 (48)
(48)
Тогда система соответствующих нормальных уравнений имеет вид:
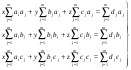 (49)
(49)
Решение системы (49) дает решение задачи (48) наилучшим приближением, в смысле дискретной нормы Гаусса.
Замечания:
1) классический метод Гаусса, метод Гаусса с выбором главного элемента, метод Якоби и метод минимизации невязки являются общими методами и применяются для определения решения невырожденных систем линейных уравнений, когда ведущие (большие по модулю) элементы матрицы системы расположены в окрестности главной диагонали (система хорошо обусловлена), если же система плохо обусловлена, тогда нужно менять соответствующую модель, чтобы она приводила к приемлемой системе уравнений;
2) для ускорения сходимости методов разработаны специальные методы – метод Гаусса-Зейделя, методы релаксации и др., которые применимы лишь для узкого класса систем – с симметрической, положительно-определенной матрицей; с ненулевыми диагональными элементами;
3) для нужд разностных уравнений разработаны специальные алгоритмы прогонки Томаса, которые являются «экономными» методами Гаусса для трехдиагональных матриц системы линейных уравнений.
Литература
Т. Шуп. Решение интегральных задач на ЭВМ. Мир., М.,2002
Л. Коллатц, Ю. Альберхт. Задачи по прикладной математике. Мир., М.,1998.
Т.А. Обгадзе. Элементы математического моделирования. Учебное пособие. Грузинский Политехнический Институт им. В.И. Ленина, Тбилисси, 1999.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ