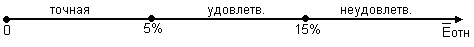
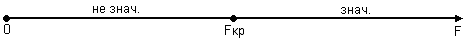
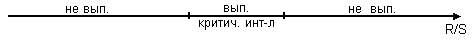
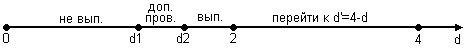
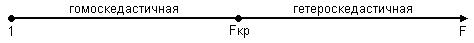
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

ФИЛИАЛ В Г. ЛИПЕЦКЕ

Контрольная работа

по эконометрике

Липецк, 2009 г.

Задача

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн.руб.) от объема капиталовложений (Х, млн.руб.)

Y

31

23

38

47

46

49

20

32

46

24

Х

38

26

40

45

51

49

34

35

42

24

Требуется:

1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков 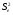; построить график остатков.

3. Проверить выполнение предпосылок МНК.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве.

6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости α=0,01 при Х=80% от его максимального значения.

7. Представить графически фактических и модельных значений Y, точки прогноза.

8. Составить уравнения нелинейной регрессии:

   • Гиперболической;

   • Степенной;

   • Показательной.

Привести графики построенных уравнений регрессии.

9. Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

Решение

1. Уравнение линейной регрессии имеет вид:

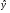= а₀ + а₁x.

Построим линейную модель.

Для удобства выполнения расчетов предварительно упорядочим всю таблицу исходных данных по возрастанию факторной переменной Х (Данные => Сортировка). ( рис. 1).

Рис.1

Используем программу РЕГРЕССИЯ и найдем коэффициенты модели (рис.2)

Рис.2

Коэффициенты модели содержатся в таблице 3 (столбец Коэффициенты).

Таким образом, модель построена и ее уравнение имеет вид

Yт = 12,70755+0,721698Х.

Коэффициент регрессии b=0,721698, следовательно, при увеличении объема капиталовложений (Х) на 1 млн руб. объем выпуска продукции (Y) увеличивается в среднем на 0,721698 млн руб.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков SІ_e; построить график остатков.

Остатки содержатся в столбце Остатки итогов программы РЕГРЕССИЯ (таблица 4).

Программой РЕГРЕССИЯ найдены также остаточная сумма квадратов SSост=148,217 и дисперсия остатков MS=18,52712 (таблица 2).

Для построения графика остатков нужно выполнить следующие действия:

• Вызвать Матер Диаграмм, выбрать тип диаграммы Точечная (с соединенными точками).

• Для указания данных для построения диаграммы зайти во вкладку Ряд, нажать кнопку Добавить; в качестве значений Х указать исходные данные Х (таблица 1);значения Y - остатки (таблица 4).

Рис.3 График остатков

3. Проверить выполнение предпосылок МНК.

Предпосылками построения классической линейной регрессионной модели являются четыре условия, известные как условия Гаусса-Маркова.

• В уравнении линейной модели Y=a+b*X+ε слагаемое ε - случайная величина, которая выражает случайный характер результирующей переменной Y.

• Математическое ожидание случайного члена в любом наблюдении равно нулю, а дисперсия постоянна.

• Случайные члены для любых двух разных наблюдений независимы (некоррелированы).

• Распределение случайного члена является нормальными.

1) Проведем проверку случайности остаточной компоненты по критерию повторных точек.

Количество повторных точек определим по графику остатков: p=5

Вычислим критическое значение по формуле:

.

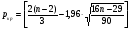При 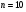найдем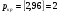

Схема критерия:

Сравним 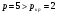, следовательно, свойство случайности для ряда остатков выполняется.

1. Равенство нулю математического ожидания остаточной компоненты для линейной модели, коэффициенты которой определены по МНК, выполняется автоматически. С помощью функции СРЗНАЧ для ряда остатков можно проверить: .

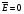Свойство постоянства дисперсии остаточной компоненты проверим по критерию Гольдфельда–Квандта.

В упорядоченных по возрастанию переменной X исходных данных (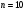) выделим первые 4 и последние 4 уровня, средние 2 уровня не рассматриваем.

С помощью программы РЕГРЕССИЯ построим модель по первым четырем наблюдениям (регрессия-1), для этой модели остаточная сумма квадратов .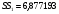

Дисперсионный анализ

df

SS

MS

F

Значимость F

Регрессия

1

107,7894737

107,7894737

15,67347

0,15751

Остаток

1

6,877192982

6,877192982

Итого

2

114,6666667

С помощью программы РЕГРЕССИЯ построим модель по последним четырем наблюдениям (регрессия-2), для этой модели остаточная сумма квадратов .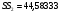

Дисперсионный анализ

df

SS

MS

F

Значимость F

Регрессия

1

4,166666667

4,166666667

0,186916

0,707647

Остаток

2

44,58333333

22,29166667

Итого

3

48,75

Рассчитаем статистику критерия:

.

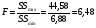Критическое значение при уровне значимости 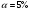и числах степеней свободы 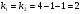составляет .

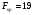Схема критерия:

Сравним 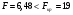, следовательно, свойство постоянства дисперсии остатков выполняется, модель гомоскедастичная.

2. Для проверки независимости уровней ряда остатков используем критерий Дарбина–Уотсона

.

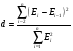Предварительно по столбцу остатков с помощью функции СУММКВРАЗН определим 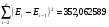; используем найденную программой РЕГРЕССИЯ сумму квадратов остаточной компоненты .

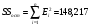Таким образом,

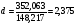
Схема критерия:

Полученное значение d=2,375, что свидетельствует об отрицательной корреляции. Перейдем к d’=4-d=1,62 и сравним ее с двумя критическими уровнями d1=0,88 и d2=1,32.

D’=1,62 лежит в интервале от d2=1,32 до 2, следовательно, свойство независимости остаточной компоненты выполняются.

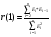
С помощью функции СУММПРОИЗВ найдем для остатков 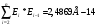, следовательно r(1)=2,4869Е-14/148,217=1,67788Е-16.

Критическое значение для коэффициента автокорреляции определяется как отношение 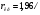n и составляет для данной задачи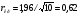

Сравнения показывает, что r(1)= 1,67788Е-16<0,62, следовательно, ряд остатков некоррелирован.

4) Соответствие ряда остатков нормальному закону распределения проверим с помощью 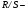критерия:

.

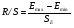С помощью функций МАКС и МИН для ряда остатков определим 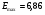, 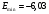. Стандартная ошибка модели найдена программой РЕГРЕССИЯ и составляет 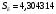. Тогда:

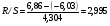
Критический интервал определяется по таблице критических границ отношения 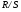и при 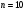составляет (2,67; 3,57).

Схема критерия:

2,995 (2,67; 3,57), значит, для построенной модели свойство нормального распределения остаточной компоненты выполняется.

Проведенная проверка предпосылок регрессионного анализа показала, что для модели выполняются все условия Гаусса–Маркова.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t–критерия Стьюдента ().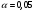

t–статистика для коэффициентов уравнения приведены в таблице 4.

Для свободного коэффициента 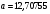определена статистика .

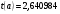Для коэффициента регрессии 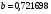определена статистика .

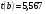Критическое значение 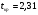найдено для уравнения значимости 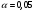и числа степеней свободы 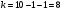с помощью функции СТЬЮДРАСПОБР.

Схема критерия:

Сравнение показывает:

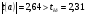, следовательно, свободный коэффициент a является значимым.

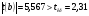, значит, коэффициент регрессии b является значимым.

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F–критерия Фишера (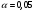), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

Коэффициент детерминации R–квадрат определен программой РЕГРЕССИЯ и составляет .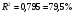

Таким образом, вариация объема выпуска продукции Y на 79,5% объясняется по полученному уравнению вариацией объема капиталовложений X.

Проверим значимость полученного уравнения с помощью F–критерия Фишера.

F–статистика определена программой РЕГРЕССИЯ (таблица 2) и составляет .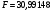

Критическое значение 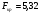найдено для уровня значимости 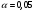и чисел степеней свободы , .

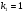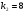Схема критерия:

Сравнение показывает: 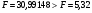; следовательно, уравнение модели является значимым, его использование целесообразно, зависимая переменная Y достаточно хорошо описывается включенной в модель факторной переменной Х.

Для вычисления средней относительной ошибки аппроксимации рассчитаем дополнительный столбец относительных погрешностей, которые вычислим по формуле

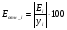
с помощью функции ABS (таблица 5).

ВЫВОД ОСТАТКА

Наблюдение

Предсказанное Y

Остатки

Отн. Погр-ти

1

27,14150943

6,858490566

20,17%

2

29,30660377

-3,306603774

12,72%

3

30,02830189

-6,028301887

25,12%

4

35,08018868

2,919811321

7,68%

5

35,80188679

-0,801886792

2,29%

6

40,13207547

-0,132075472

0,33%

7

45,90566038

-3,905660377

9,30%

8

45,90566038

5,094339623

9,99%

9

46,62735849

-1,627358491

3,62%

10

48,07075472

0,929245283

1,90%

По столбцу относительных погрешностей найдем среднее значение 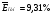(функция СРЗНАЧ).

Схема проверки:

Сравним: 9,31% < 15%, следовательно, модель является точной.

Вывод: на основании проверки предпосылок МНК, критериев Стьюдента и Фишера и величины коэффициента детерминации модель можно считать полностью адекватной. Дальнейшее использование такой модели для прогнозирования в реальных условиях целесообразно.

6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости 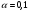, если прогнозное значение фактора X составит 80% от его максимального значения.

Согласно условию задачи прогнозное значение факторной переменной Х составит 80% от 49, следовательно, 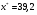. Рассчитаем по уравнению модели прогнозное значение показателя У:

.

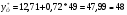Таким образом, если объем капиталовложений составит 39,2 млн. руб., то ожидаемый объем выпуска продукции составит около 48 млн. руб.

Зададим доверительную вероятность 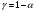и построим доверительный прогнозный интервал для среднего значения Y.

Для этого нужно рассчитать стандартную ошибку прогнозирования:

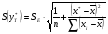
Предварительно подготовим:

- стандартную ошибку модели 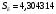(Таблица 2);

- по столбцу исходных данных Х найдем среднее значение 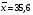(функция СРЗНАЧ) и определим 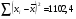(функция КВАДРОТКЛ).

Следовательно, стандартная ошибка прогнозирования для среднего значения составляет:

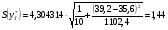
При 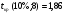размах доверительного интервала для среднего значения

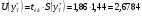
Границами прогнозного интервала будут

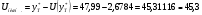
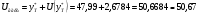
Таким образом, с надежностью 90% можно утверждать, что если объем капиталовложений составит 39,2 млн. руб., то ожидаемый объем выпуска продукции будет от 45,3 млн. руб. до 50,67 млн. руб.

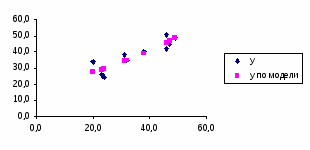
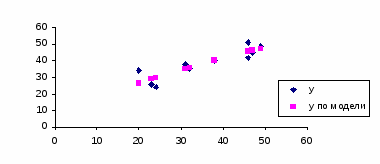
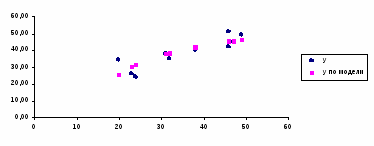
7. Представить графически фактические и модальные значения Y точки прогноза.

Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные (поле корреляции).

Затем с помощью опции Добавить линию тренда… построим линию модели:

тип → линейная; параметры → показывать уравнение на диаграмме.

Покажем на графике результаты прогнозирования. Для этого в опции Исходные данные добавим ряды:

Имя → прогноз; значения 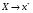; значения ;

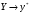Имя → нижняя граница; значения 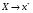; значения ;

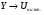Имя → верхняя граница; значения 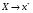; значения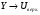

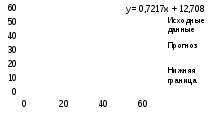
8. Составить уравнения нелинейной регрессии: гиперболической; степенной; показательной.

8.1 Гиперболическая модель

Уравнение гиперболической функции:

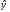= a + b/x.

Произведем линеаризацию модели путем замены X = 1/x. В результате получим линейное уравнение

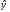= a + bX.

Рассчитаем параметры уравнения по данным таблицы 2.

b = =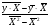

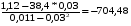
а = 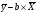=38,4+704,48*0,03=60,25.

Получим следующее уравнение гиперболической модели:

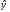= 60,25-704,48/х.

8.2 Степенная модель

Уравнение степенной модели имеет вид: 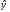=аx^b

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:

lg 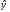= lg a + b lg x.

Обозначим через

Y=lg 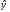, X=lg x, A=lg a.

Тогда уравнение примет вид: Y = A + bX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 3.

b = =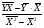

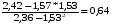
A = 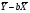= 1,57-0,64*1,53=0,59

Уравнение регрессии будет иметь вид: Y = 0,59+0,64* Х.

Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения.

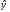= 10^0,59* х^0,64.

Получим уравнение степенной модели регрессии:

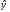= 3,87* х^0,64.

8.3 Показательная модель

Уравнение показательной кривой: 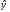=ab^x.

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:

lg 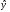= lg a + x lg b.

Обозначим: Y = lg 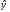, B = lg b, A = lg a. Получим линейное уравнение регрессии: Y = A + B x. Рассчитаем его параметры, используя данные таблицы 4.

В = =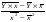

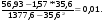
А =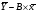 = 1,57-0,01*35,6=1,27

Уравнение будет иметь вид: Y = 1,27+0,01х.

Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:

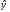=10^1,27* ( 10^0,01)^х = 18,55*1,02^х.

Графики построенных моделей:

Рис.3. Гиперболическая

Рис.4. Степенная

Рис.5. Показательная

9. Сравнение моделей по характеристикам: коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Вывод.

9.1 Гиперболическая модель

Коэффициент детерминации:

=

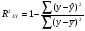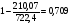
Вариация результата Y на 70,9% объясняется вариацией фактора Х.

Коэффициент эластичности:

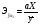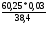= = 0,05.

Это означает, что при увеличении фактора Х на 1 % результирующий показатель изменится на 0,05 %.

Бета-коэффициент:

S_x=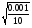=0,01 S_y=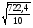=8,5 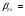60,25*0,01/8,5=0,07.

Т.е. увеличение объема капиталовложений на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения объема выпуска продукции на 0,07 среднеквадратического отклонения этого показателя.

Средняя относительная ошибка аппроксимации:

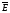_отн = 109,7/ 10= 10,97 %.

В среднем расчетные значения 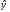для гиперболической модели отличаются от фактических значений на 10,97%.

9.2 Степенная модель

Коэффициент детерминации:

=

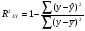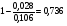
Вариация результата Y на 73,6% объясняется вариацией фактора Х. Коэффициент эластичности:

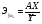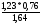= = 0,57.

Это означает, что при увеличении факторного признака на 1 % результирующий показатель увеличится на 0,57%.

Бета-коэффициент:

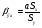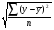, S_y= и S_x=.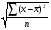

S_x=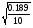=0,14 S_y=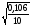=0,10 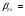0,59*0,14/0,1=0,78.

Т.е. увеличение объема капиталовложений на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения объема выпуска продукции на 0,78 среднеквадратического отклонения этого показателя.

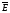_отн= 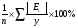= 93,77/10 = 9,34%.

В среднем расчетные значения 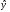для степенной модели отличаются от фактических значений на 9,34%.

9.3 Показательная модель

Коэффициент детерминации:

=

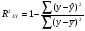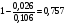
Вариация результата Y на 75,7% объясняется вариацией фактора Х. Коэффициент эластичности:

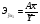
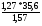= 28,71.

Это означает, что при росте фактора Х на 1 % результирующий показатель Y изменится на 28,71 %.

Бета-коэффициент:

S_x=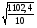=10,5 S_y=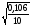=0,10 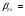1,27*10,5/0,10=129,10.

Т.е. увеличение объема капиталовложений на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения объема выпуска продукции на 129,1 среднеквадратического отклонения этого показателя.

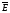_отн= 91,9/ 10 = 9,19%.

В среднем расчетные значения 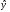для показательной модели отличаются от фактических значений на 9,19%.

Вывод

Лучшей из уравнений нелинейной регрессии является показательная: выше коэффициент детерминации, наименьшая относительная ошибка. Модель можно использовать для прогнозирования.