Многомерные и многосвязные системы
Контрольная работа
«Многомерные и многосвязные системы»
Задание
Для многомерной системы, заданной матрицами А, В, С, получить:
1. Передаточную функцию 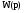 ;
;
2. Частотную передаточную функцию 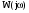 ;
;
3. Годограф;
4. Импульсную характеристику 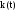 ;
;
5. Переходную характеристику 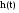 ;
;
6. ЛАЧХ 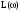 ;
;
7. ФЧХ 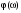 .
.
Составить структурную схему системы.
Дано:
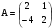 ;
;
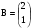 ;
;
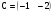 .
.
Решение:
1. Передаточная функция
Рассматриваем линейную систему с постоянными параметрами:
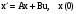 ,
,
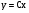 .
.
Преобразуем по Лапласу матричные уравнения:
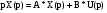 ; (1)
; (1)
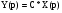 , (2)
, (2)
где
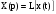 ;
; 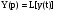 ;
; 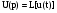
– лапласовы преобразования координат состояния 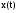 , выходных
, выходных 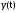 и входных
и входных 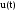 сигналов.
сигналов.
Преобразуем уравнение (1):
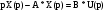
Выносим за скобки:
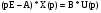
где
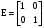 – единичная матрица.
– единичная матрица.
Умножаем слева на обратную матрицу:
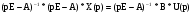
Откуда получаем:
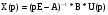 .
.
Подставляем в уравнение (2):
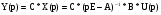
Получаем:
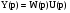
Выражение 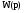 называют передаточной функцией системы.
называют передаточной функцией системы.
Находим её:
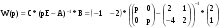
Находим обратную матрицу:

Подставляем:
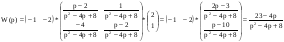 .
.
2. Частотная передаточная функция
Для получения частотной передаточной функции производим замену в передаточной функции 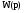 :
:
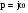 ,
,
получаем:
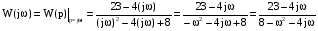 .
.
Выделим действительную и мнимую части:
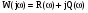 ,
,
для этого умножим числитель и знаменатель 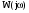 на комплексно – сопряжённый знаменатель:
на комплексно – сопряжённый знаменатель:
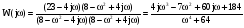 ;
;
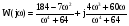 ;
;
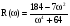 ;
;
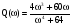 .
.
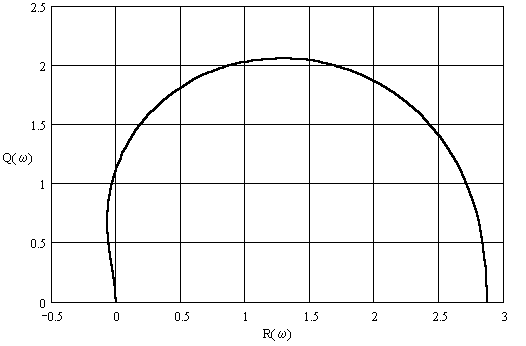
3. Годограф
Годограф – это график частотной передаточной функции 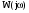 на комплексной плоскости при изменении частоты
на комплексной плоскости при изменении частоты 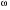 от нуля до бесконечности.
от нуля до бесконечности.
Изменяя частоту, производим расчёт действительной 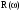 и мнимой
и мнимой 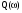 частей частотной передаточной функции.
частей частотной передаточной функции.
Результат расчёта записываем в таблицу 1.
Таблица 1. Расчёт годографа
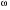
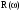
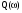
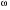
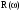
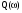
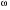
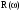
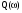
0
2,8750000
0,0000000
10
-0,0512719
0,4570747
200
-0,00018
0,020008
1
2,7230769
0,9846154
20
-0,0163435
0,2074170
300
-0,000078
0,013336
2
1,9500000
1,9000000
30
-0,0075500
0,1355448
400
-0,000044
0,010001
3
0,8344828
1,9862069
40
-0,0043030
0,1009350
500
-0,000028
0,008001
4
0,2250000
1,5500000
50
-0,0027705
0,0804792
600
-0,000019
0,006667
5
0,0130624
1,1611030
60
-0,0019302
0,0669441
700
-0,000014
0,005715
6
-0,0500000
0,9000000
70
-0,0014209
0,0573176
800
-0,000019
0,005000
7
-0,0645030
0,7269777
80
-0,0010893
0,0501171
900
-0,000009
0,004445
8
-0,0634615
0,6076923
90
-0,0008614
0,0445267
1000
-0,000007
0,004000
9
-0,0578113
0,5216604
100
-0,0006982
0,0400600
2000
-0,000002
0,002000
Можно построить график на комплексной плоскости – рис. 1.
Рис. 1. Годограф
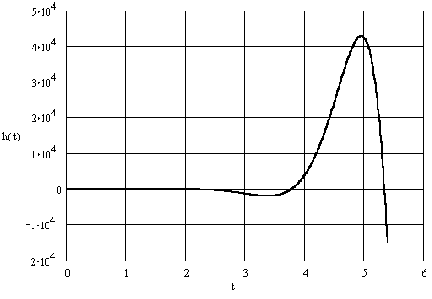
4. Импульсная характеристика
Импульсная характеристика вычисляется как обратное преобразование Лапласа от передаточной функции:
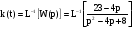 .
.
Найдём полюса передаточной функции:
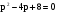
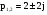
Видим – полюса расположены в правой полуплоскости, а это значит, что процесс будет расходящимся.
Разложим передаточную функцию на простые дроби:
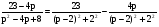 .
.
Используя табличные значения, находим:
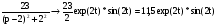 ,
,
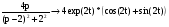 .
.
Таким образом, получаем:
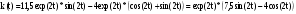 .
.
Изменяя время от нуля до 5 секунд, производим расчёт по формуле, результаты заносим в таблицу 2.
Таблица 2. Импульсная характеристика

0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
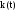
-4
11,28
62,69
100,8
-167,1
-1236
-2395
2097
23854
54578
-15944
Строим график импульсной характеристики – рис. 2.
Рис. 2. Импульсная характеристика
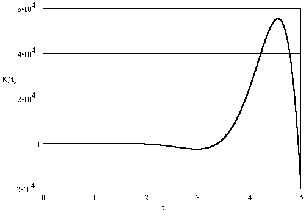
5. Переходная характеристика
Переходная характеристика вычисляется как обратное преобразование Лапласа от передаточной функции, делённой на р:
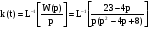 .
.
Найдём полюса передаточной функции:
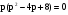
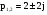 ;
; 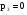 .
.
Видим – полюса расположены в правой полуплоскости, а это значит, что процесс будет расходящимся.
Разложим передаточную функцию, делённую на р, на простые дроби:
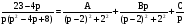 .
.
Приводим к общему знаменателю:
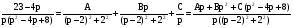 .
.
Приравниваем коэффициенты при равных степенях р:
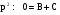 ,
,
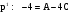 ,
,
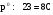 .
.
Откуда находим:
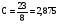 ,
,
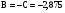 ,
,
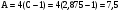 .
.
Используя табличные значения, находим:
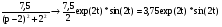 ,
,
 ,
,
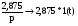 .
.
Таким образом, получаем:
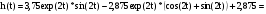
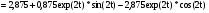 .
.
Изменяя время от нуля до 5 секунд, производим расчёт по формуле, результаты заносим в таблицу 3.
Таблица 3. Переходная характеристика

0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
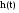
0
0,654
17,59
62,52
69,32
-243
-1209
-1744
3830
24151
42653
Строим график переходной характеристики – рис. 3.
Рис. 3. Переходная характеристика
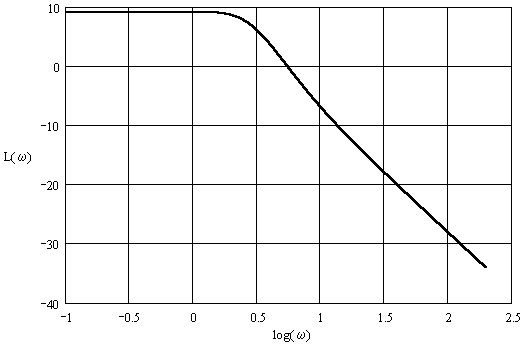
6. ЛАЧХ
Для получения ЛАЧХ найдём модуль частотной передаточной функции:
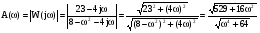 .
.
далее находим 20 десятичных логарифмов от найденного модуля:
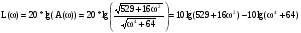 .
.
Это и есть выражение для ЛАЧХ.
Расчёт значений ЛАЧХ ведём в логарифмическом масштабе. Результаты записываем в таблицу 4. Размерность ЛАЧХ – децибелы (дБ).
Таблица 4. ЛАЧХ
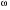
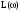
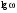
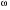
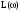
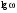
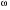
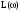
-1
0,1
9,17406
0,1
1,25893
9,20891
1,2
15,8489
-11,426
-0,9
0,12589
9,17482
0,2
1,58489
9,08243
1,3
19,9526
-13,614
-0,8
0,15849
9,17601
0,3
1,99526
8,70564
1,4
25,1189
-15,738
-0,7
0,19953
9,17788
0,4
2,51189
7,83066
1,5
31,6228
-17,818
-0,6
0,25119
9,18077
0,5
3,16228
6,23375
1,6
39,8107
-19,869
-0,5
0,31623
9,18519
0,6
3,98107
3,94960
1,7
50,1187
-21,902
-0,4
0,39811
9,19182
0,7
5,01187
1,26946
1,8
63,0957
-23,923
-0,3
0,50119
9,20135
0,8
6,30957
-1,5050
1,9
79,4328
-25,936
-0,2
0,63096
9,21400
0,9
7,94328
-4,1982
2
100
-27,944
-0,1
0,79433
9,22792
1
10
-6,7459
2,1
125,893
-29,950
0
1
9,23483
1,1
12,5893
-9,1470
2,2
158,489
-31,953
Строим график ЛАЧХ – рис. 4.
Рис. 4. ЛАЧХ
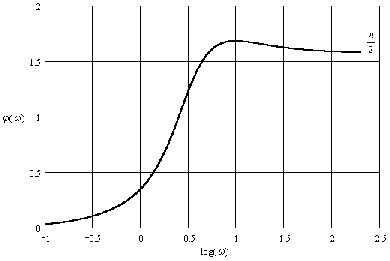
7. ФЧХ
ФЧХ – угол поворота вектора 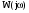 на комплексной плоскости в зависимости от частоты:
на комплексной плоскости в зависимости от частоты:
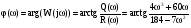 .
.
Расчёт значений ФЧХ ведём в логарифмическом масштабе. Результаты записываем в таблицу 5. Размерность ФЧХ – радианы (рад).
Таблица 5. ФЧХ
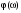
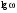
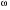
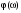
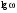
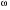
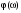
-1
0,1
0,03263
0,1
1,25893
0,44997
1,2
15,8489
1,66382
-0,9
0,12589
0,04110
0,2
1,58489
0,58831
1,3
19,9526
1,64958
-0,8
0,15849
0,05177
0,3
1,99526
0,77030
1,4
25,1189
1,63592
-0,7
0,19953
0,06524
0,4
2,51189
0,99225
1,5
31,6228
1,62384
-0,6
0,25119
0,08227
0,5
3,16228
1,22480
1,6
39,8107
1,61359
-0,5
0,31623
0,10383
0,6
3,98107
1,42316
1,7
50,1187
1,60513
-0,4
0,39811
0,13123
0,7
5,01187
1,56064
1,8
63,0957
1,59824
-0,3
0,50119
0,16622
0,8
6,30957
1,63913
1,9
79,4328
1,59268
-0,2
0,63096
0,21126
0,9
7,94328
1,67427
2
100
1,58822
-0,1
0,79433
0,26981
1
10
1,68250
2,1
125,893
1,58466
0
1
0,34696
1,1
12,5893
1,67633
2,2
158,489
1,58182
Строим график ФЧХ – рис. 5.
Рис. 5. ФЧХ
8. Структурная схема системы
Записываем матричные уравнения системы:
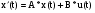 ;
;
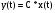 .
.
Подставляем исходные данные:
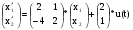 ;
;
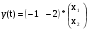 .
.
Производим умножение матриц:
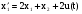 ,
,
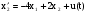 ,
,
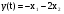 .
.
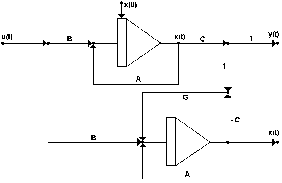
Получили систему уравнений, на основе которой строим структурную схему – рис. 6.
Рис. 6. Структурная схема системы
Часть 2:
Осуществить синтез замкнутой системы с собственными числами
{–1; –4; 5j}.
Построить наблюдатель полного порядка.
Дано:
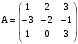 ,
,
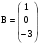 ,
,
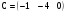 .
.
Решение:
1. Синтез замкнутой системы
Рассматриваем линейную систему с постоянными параметрами:
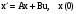 ,
,
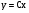 .
.
Пусть управление линейно зависит от координат состояния системы:
 ,
,
где
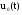 – входной командный сигнал,
– входной командный сигнал,
К – матрица коэффициентов обратной связи.
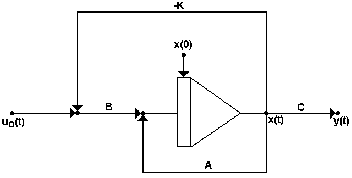
После замыкания эта система имеет структуру, изображённую на рис. 7.
Рис. 7. Структура исходной системы
Движение системы описывается линейным дифференциальным уравнением:
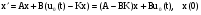 .
.
Таким образом, динамические свойства системы полностью определяются матрицей А – ВК, её характеристическими числами.
Характеристический многочлен исходной системы равен:
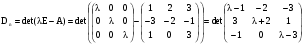
 .
.
Спектр характеристических чисел (корни характеристического многочлена):
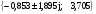 .
.
Желаемый характеристический многочлен замкнутой системы 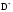 по условию имеет 4 собственных числа, но наша исходная система имеет третий порядок, поэтому одно из собственных чисел необходимо убрать, убираем собственное число (–1), тогда:
по условию имеет 4 собственных числа, но наша исходная система имеет третий порядок, поэтому одно из собственных чисел необходимо убрать, убираем собственное число (–1), тогда:
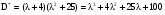 .
.
Пусть матрица коэффициентов обратной связи 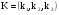 , тогда характеристический полином замкнутой системы:
, тогда характеристический полином замкнутой системы:
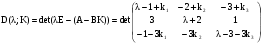
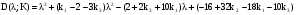 .
.
Приравниваем коэффициенты при равных степенях многочленов 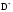 и
и 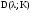 :
:
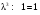 ,
,
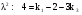 ,
,
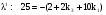 ,
,
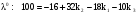 .
.
Решая полученную систему уравнений, получаем:
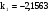 ,
,
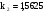 ,
,
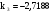 .
.
Искомое управление принимает вид:
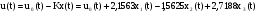 .
.
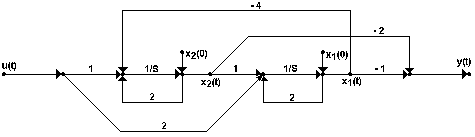
Структура синтезированной системы представлена на рис. 8.
Она построена по уравнениям:
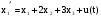 ,
,
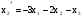 ,
,
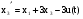 ,
,
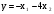 ,
,
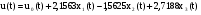 .
.
Рис. 8. Структура синтезированной системы
2. Построение наблюдателя полного порядка
Система
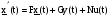
называется асимптотическим наблюдателем полного порядка, если для любого начального состояния х(0) и всех 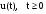 оценка
оценка 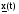 с ростом времени асимптотически приближается к вектору состояния
с ростом времени асимптотически приближается к вектору состояния 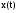 .
.
Найдём структуру асимптотического наблюдателя, для чего определим ошибку восстановления 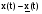 и найдём модель её изменения:
и найдём модель её изменения:
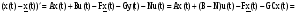
 .
.
Затем потребуем, чтобы 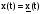 при всех
при всех 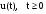 и
и 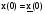 .
.
Это равенство возможно при:
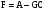 ,
,
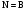 .
.
Таким образом, структура асимптотического наблюдателя полного порядка определяется моделью вида:
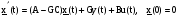 .
.
На рис. 9 изображена структура системы и её наблюдателя.
Рис. 9. Структура системы с наблюдателем
Задача синтеза наблюдателя системы состоит в том, чтобы найти матрицу 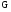 . Это можно сделать, исходя из условия асимптотической сходимости оценки
. Это можно сделать, исходя из условия асимптотической сходимости оценки 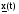 к вектору состояния
к вектору состояния 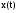 при любых начальных состояниях наблюдателя и системы.
при любых начальных состояниях наблюдателя и системы.
Пусть ошибка восстановления 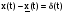 , тогда
, тогда
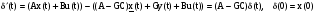 .
.
Ошибка восстановления описывается линейным однородным дифференциальным уравнением с матрицей 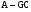 и ненулевыми начальными условиями, а поэтому асимптотическая сходимость ошибки к нулю возможна тогда и только тогда, когда собственные числа матрицы
и ненулевыми начальными условиями, а поэтому асимптотическая сходимость ошибки к нулю возможна тогда и только тогда, когда собственные числа матрицы 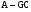 , которые называют полюсами наблюдателя, располагаются в левой полуплоскости.
, которые называют полюсами наблюдателя, располагаются в левой полуплоскости.
Пусть матрица
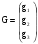 ,
,
тогда матрица
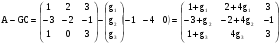 .
.
Полюса наблюдателя определяются уравнением:
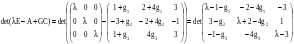
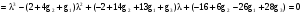 .
.
Переходные процессы в наблюдателе будут несравнимы с процессами в системе, если полюса наблюдателя будут значительно левее полюсов системы. Поскольку характеристические числа замкнутой системы равны:
{– 4; 5j},
то расположим полюса наблюдателя в точках:
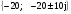 .
.
Желаемый характеристический полином наблюдателя принимает вид:
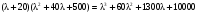 ,
,
что будет иметь место тогда, когда:
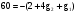 ,
,
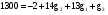 ,
,
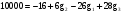 .
.
Решая полученную систему уравнений, получаем:
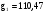 ;
;
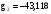 ;
;
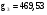 .
.
Находим матрицу:
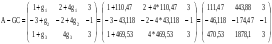
Модель асимптотического наблюдателя системы принимает вид:
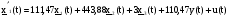 ,
,
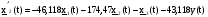 ,
,
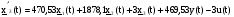 ,
,
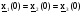 .
.
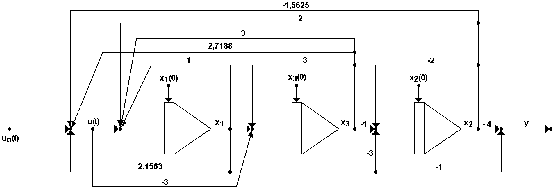
Структура системы со своим асимптотическим наблюдателем полного порядка представлена на рис. 10.
Она построена по уравнениям:
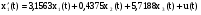 ,
,
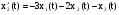 ,
,
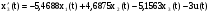 ,
,
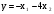 ,
,
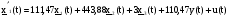 ,
,
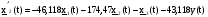 ,
,
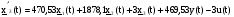 .
.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ