Модель распределения

Курсовая работа по статистике

Работу выполнил ст. гр. ЭР-6-4 Шалыгин Д.А.

Московский государственный технологический университет «Станкин»

Кафедра «Производственный менеджмент»

Москва 2001

Раздел 1. Исследование модели распределения

1. Формирование выборочной совокупности

Обычно бывает затруднительно исследовать генеральную совокупность. Тогда проводят исследование выборочной совокупности, и его результаты распространяют на генеральную совокупность.

Наиболее часто для формирования выборочной совокупности применяют бесповторную случайную выборку. Случайный отбор организуют с помощью жребия, таблицы случайных чисел или программы, генерирующей квазислучайную последовательность чисел. Для этого единицы генеральной совокупности нумеруют. Данные, соответствующие выпавшим, номерам попадают в выборку. При этом повторяющиеся номера пропускаем.

Покажем применение таблицы случайных чисел. В табл. 1 приложения приведено пятьсот четырехзначных случайных чисел.

Рассмотрим пример получения выборки. Генеральная совокупность содержит значения восьми количественных экономических показателей для 100 предприятий. Она представлена в табл.2 приложения.

Наиболее проработанной в статистике является парная корреляция. Положим, нужно установить корреляционную связь между двумя показателями. В нашем случае мы изучаем связь между годовой балансовой прибылью (показатель 5) и электровооруженностью на одного работающего (показатель №7), выбираем в табл.1 приложения четырёхзначное число из 7-го столбца, 5-ой строки; т.к. сумма номеров показателей чётна, то из него берём правую половину; далее выбираем 30 неповторяющихся чисел. Затем из табл.2 приложения выбираем в соответствующих номерах строк 30 пар значений изучаемых показателей, в соответствии с этими данными получаем табл.1.1

Таблица 1.1

№ строки

5

7

5

40,2

35,6

12

35,4

32,9

13

31,4

30,5

18

42,8

37,7

22

36,6

33,7

26

37,8

34,3

27

44,5

38,4

30

42,7

37,2

31

32,8

31,3

32

32,5

30,7

36

32,7

31,4

38

38,9

35,3

40

33,2

31,6

41

36,2

33,7

43

33,3

31,4

45

36,2

33,5

46

38,4

34,6

49

38,8

35,1

52

35,7

33,2

54

33,7

32

57

36,3

33,6

60

40,3

36,1

65

35,8

32,8

68

33,7

31,9

69

41,6

36,3

71

38,8

35

76

34,9

32,6

80

39,4

35,8

86

37,1

33,5

91

35,9

32,6

99

4

42,2

2. Построение интервального ряда распределения

Этот и последующие этапы работы в этом разделе выполняем для каждого изучаемого признака в отдельности.

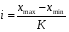Принимая во внимание, что выборочная совокупность содержит n значений, величину равных интервалов выбираем по формуле Г.А. Стерджесса:

где К = 1+3,322gn- число интервалов; при n=30 К=5. xmax и xmin - минимальное и максимальное значения признака.

Определяем границы интервалов. Для первого интервала левая граница равна xmin, а правая – xmin +i и, для второго, соответственно - xmin +i и xmin +2i и т.д.

Строим таблицу частоты распределения значений признака по интервалам и гистограмму. Для определенности считаем, что значение признака, лежащее на границе двух интервалов, попадает в правый интервал.

Для показателя x: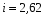

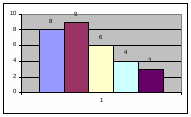
Определяем границы интервалов и строим таблицу частоты распределения значений признака по интервалам:

Границы интервалов

Число предприятий

31,4

34,02

8

34,02

36,64

9

36,64

39,26

6

39,26

41,88

4

41,88

44,5

3

Строим гистограмму:

Для показателя y: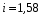

Определяем границы интервалов и строим таблицу частоты распределения значений признака по интервалам:

Границы интервалов

Число предприятий

30,5

32,08

8

32,08

33,66

8

33,66

35,24

6

35,24

36,82

5

36,82

38,4

3

Строим гистограмму:

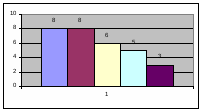
3. Проверка соответствия эмпирического распределения нормальному закону распределения

Для проверки соответствия эмпирического распределения случайной величины нормальному закону распределения в нашем случае (при n<30) можно использовать критерии Шапиро-Уилкса (W) и Колмогорова (D). В нашем случае мы используем критерий Колмогорова.

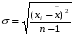
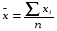Сначала определим среднюю величину 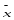и среднее квадратическое отключение от нее, считая выборку малой:

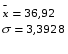Для признака x:

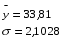Для признака y:

Вычисляем ошибку определения средней по выборочной совокупности (ошибку выборки):

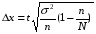где n - численность выборки; N= 100 - численность генеральной совокупности; t - коэффициент доверия; при доверительной вероятности 95,45% t=2.

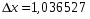
Для признака x:

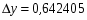
Для признака y:

Генеральная средняя располагается в следующих границах:

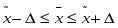
Определяем эти границы:

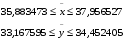
Ранжируем значения величин x и y по возрастанию (табл.1.2.):

x₁ x₂  … x_n-1 x_n

Таблица 1.2.

X

Y

1

2

31,4

30,5

32,5

30,7

32,7

31,4

32,8

31,3

33,2

31,6

33,3

31,4

33,7

32

33,7

31,9

34,9

32,6

35,4

32,9

35,7

33,2

35,8

32,8

35,9

32,6

36,2

33,7

36,2

33,5

36,3

33,6

36,6

33,7

37,1

33,5

37,8

34,3

38,4

34,6

38,8

35,1

38,8

35

38,9

35,3

39,4

35,8

40,2

35,6

40,3

36,1

41,6

36,3

42,7

37,2

42,8

37,7

44,5

38,4

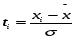Перейдем к нормированным значениям аргумента (табл.1.3):

Таблица 1.3.

t(x)

F(tx)

t(y)

F(ty)

1

2

3

4

5

t1

-1,6

0,0548

-1,6

0,0548

t2

-1,3

0,0968

-1,5

0,0668

t3

-1,2

0,1151

-1,2

0,1151

t4

-1,2

0,1151

-1,1

0,1357

t5

-1,1

0,1357

-1,1

0,1357

t6

-1,1

0,1357

-1,1

0,1357

t7

-0,9

0,1841

-0,9

0,1841

t8

-0,9

0,1841

-0,9

0,1841

t9

-0,6

0,2743

-0,6

0,2743

t10

-0,4

0,3446

-0,6

0,2743

t11

-0,4

0,3446

-0,5

0,3085

t12

-0,3

0,3821

-0,4

0,3446

t13

-0,3

0,3821

-0,3

0,3821

t14

-0,2

0,4207

-0,1

0,4602

t15

-0,2

0,4207

-0,1

0,4602

t16

-0,2

0,4207

-0,1

0,4602

t17

-0,1

0,4602

-0,1

0,4602

t18

0,1

0,5398

-0,1

0,4602

t19

0,3

0,6179

0,2

0,5793

t20

0,4

0,6554

0,4

0,6554

t21

0,6

0,7257

0,6

0,7257

t22

0,6

0,7257

0,6

0,7257

t23

0,6

0,7257

0,7

0,7580

t24

0,7

0,7580

0,9

0,8159

t25

1,0

0,8413

0,9

0,8159

t26

1,0

0,8413

1,1

0,8643

t27

1,4

0,9192

1,2

0,8846

t28

1,7

0,9554

1,6

0,9452

t29

1,7

0,9554

1,8

0,9641

t30

2,2

0,9861

2,2

0,9861

Принимаем значения эмпирической функции распределения в точке t равным следующему значению (табл.1.4):

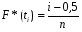
где i= 1, 2,...,n. При t< t₁ F*(t)=0, а при t>t_n F*(t)=l.

Таблица 1.4.

F*(t_i)

1

2

1

0,016667

2

0,05

3

0,083333

4

0,116667

5

0,15

6

0,183333

7

0,216667

8

0,25

9

0,283333

10

0,316667

11

0,35

12

0,383333

13

0,416667

14

0,45

15

0,483333

16

0,516667

17

0,55

18

0,583333

19

0,616667

20

0,65

21

0,683333

22

0,716667

23

0,75

24

0,783333

25

0,816667

26

0,85

27

0,883333

28

0,916667

29

0,95

30

0,983333

Определим максимальное значение модуля разности между эмпирической функцией распределения F*(t) и теоретической функцией для нормального закона распределения F(t) (значения F(t) представлены в табл.3.2):

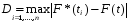
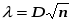
и определяем величину:

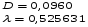Для признака x:

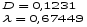Для признака y:

Затем по таблице определяем в зависимости от  вероятность Р(), того что за счёт чисто случайных причин расхождение между F*(t) и F(t) будет не больше, чем фактически наблюдаемое.

При сравнительно больших Р() теоретический закон распределения можно считать совместимым с опытными данными.

Раздел 2. Исследование взаимосвязи двух количественных признаков

1. Оценка тесноты корреляционной связи

Из логических соображений выдвинем предположение, что признак (названный нами y) зависит от второго исследуемого признака x.

Используя проведенное в первом разделе разбиение значений x на интервалы, построим аналитическую таблицу:

Аналитическая таблица исследования зависимости признака y от признака x

Группы предприятий по признаку x

Число предприятий в j-ой группе m_j

Признак y

Суммарное значение в группе

Среднее значение признака y_i в j-ой группе на одно предприятие

31,4 – 34,02

8

250,8

31,3500

34,02 – 36,64

9

298,6

33,1778

36,64 – 39,26

6

207,8

34,6333

39,26 – 41,88

4

143,8

35,9500

41,88 – 44,5

3

113,3

37,7667

Далее рассчитываем общую дисперсию:

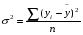
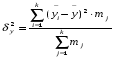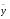где - среднее значение признака для всей выборки, и межгрупповую дисперсию:

где 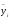- среднее значение признака в j-й группе; m_j- численность j-й группы; k - число групп.

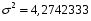
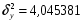
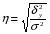Для оценки тесноты связи между признаками y и x рассчитываем корреляционное отношение:

Оценку тесноты связи признаков y и x проводим по шкале Чеддока:

-если 0,3<0,5, то теснота связи заметная;

-если 0,5<0,7, то теснота связи умеренная;

-если 0,7<0,9, то теснота связи высокая;

-если 0,9<0,9(9), то теснота связи весьма высокая.

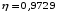
2. Определение формы связи двух признаков

Примерное представление о виде зависимости y от x даёт линия, проведённая через точки, соответствующие групповым средним и полученные на основе аналитической таблицы следующим образом: среднему значению признака 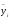в j-ой группе ставится в соответствие не середина интервала группирования по признаку x, а среднее значение 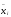, полученное из соответствующих интервалу значений признака x. Можно воспользоваться следующим приемом: построим все точки, соответствующие парам (х_i;у_i), в декартовой системе координат и провести линию через середины скоплений точек (График № 1).

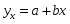Затем по справочнику плоских кривых и виду линии подбираем соответствующее уравнение регрессии. Однако не следует брать слишком сложное уравнение. В нашем случае берём линейную функцию:

Вычислив частные производные и приравняв их к нулю, получим систему линейных алгебраических уравнений относительно коэффициентов а и b. В нашем случае система уравнений имеет вид:

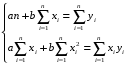
Решая эту систему уравнений относительно b, получим:

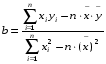
Решая первое уравнение относительно а, получим:

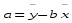
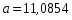
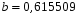
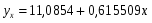Т.о.:

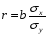Линейный коэффициент корреляции равен:

где _x и _y - средние квадратические отклонения признаков x и y.

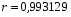
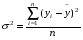Рассчитаем общую дисперсию:

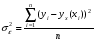и остаточную дисперсию:

где y_x(х_i) - значение величины y, рассчитанное по уравнению регрессии при подстановке в него значения x_i; y_i- значение величины y в исходной таблице, соответствующее значению x_i.

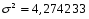
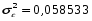
Определим индекс корреляции:

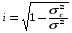
Индекс корреляции принимает значения 0 i 1.

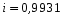
Т.к. i близок к единице, то связь между признаками хорошо описана выбранным уравнением регрессии. Для линейной зависимости дополнительным условием для такого заключения является близость значений r и i.

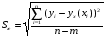Можно выбрать несколько видов уравнения регрессии. Наилучшим из них будет то уравнение, которому соответствует меньшая средняя квадратическая ошибка уравнения регрессии:

где m - число коэффициентов в уравнении регрессии.

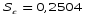
Принимая во внимание то, что мы имеем дело с малой выборкой, необходимо оценить значимость коэффициентов уравнения регрессии, а также индекса корреляции i и линейного коэффициента корреляции r. Значимость линейного коэффициента корреляции r оцениваем с помощью критерия Стьюдента. Фактическое значение критерия Стьюдента равно:

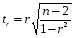
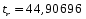
Критическое (предельное) значение критерия Стьюдента t_k, берем из табл.4 приложения, задаваясь уровнем значимости =5,0 и имея число степеней свободы равное:

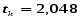k=n-2

Если t_r>t_k, то величину линейного коэффициента корреляции считаем значимой и можем использовать в расчетах.

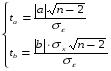Значимость коэффициентов уравнения регрессии а и b также оцениваем с помощью критерия Стьюдента. Расчетные значения критерия Стьюдента равны:

Учитывая, что число степеней свободы также равно k=n-2, сравнение фактических значений критерия Стьюдента ведем с уже найденным критическим значением t_k.

Если t_a>t_k, t_b>t_k, то соответствующий коэффициент уравнения регрессии значим, и мы можем им пользоваться. Значимость индекса корреляции определяем с помощью критерия Фишера. Фактическое значение критерия Фишера равно:

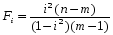где m - число коэффициентов в уравнении регрессии.

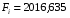
Табличное значение критерия Фишера F_k; определяется по табл.5 приложения, задаваясь уравнением значимости  и числом степеней свободы k₁=m-l; k₂=n-m.

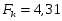
Если Fi>Fk, то величину индекса корреляции считаем значимой и можем ее использовать в расчетах.

Если коэффициенты а и b, а также линейный коэффициент корреляции r и индекс корреляции i значимы, то все наши расчеты и выводы, опирающиеся на эти величины, правомерны и мы можем использовать полученное уравнение регрессии для прогноза. Ошибка прогноза будет зависеть, в частности, от остаточной дисперсии ²_.

Раздел 3. Изучение динамических рядов

1. Изучение сезонных явлений

Исследуем сезонные процессы в наших двух динамических рядах. При изучении сезонных явлений из уровней динамического ряда целесообразно вычесть значения, получаемые по уравнению тренда, которые отражают основную тенденцию развития.

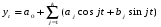При изучении периодических процессов в качестве аналитической модели используем ряд Фурье:

где k=1; j=1.

Для нахождения коэффициентов a₀, a_j, b_j применяем метод наименьших квадратов.

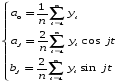Получаем:

Для признака x: Для признака y:

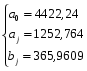
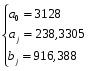
Обычно для расчётов используют ежемесячные данные за один год или несколько лет. В этом случае интервал между двумя соседними месяцами принимают равным:

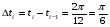
Построив модель сезонных колебаний, положим для уточнённого изучения основной тенденции a₀ =0. Исключим сезонные колебания из уровней динамического ряда (табл.3.1.1).

Таблица 3.1.1

x_t

y_t

2661,669

3613,236

2875,587

3822,011

2963,355

3982,202

3123,42

4283,029

3220,836

4428,087

3326,98

4610,676

3286,852

4566,172

3263,324

4538,486

3116,237

4319,251

3036,962

4198,99

2900,234

3993,958

2894,491

3990,848

2874,626

3974,423

2997,766

4181,021

3084,173

4339,299

3262,659

4638,991

3338,698

4783,995

3444,038

4907,625

3403,894

4924,979

3381,141

4899,469

3315,414

4682,148

3157,719

4563,026

3022,368

4358,052

3017,432

4353,904

2997,586

4365,623

2. Определение основной тенденции развития

Для выявления основной тенденции развития применяют аналитическое выравнивание. В результате выравнивания получают зависимость изучаемого показателя от времени, т.е. трендовую модель. Используем линейную трендовую модель:

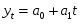
Наиболее тщательно выбирают модель для целей экстраполяции значений показателя. Значение х и у выбираем из табл.6 приложения.

Коэффициенты уравнения определяем методом наименьших квадратов. В нашем случае система уравнений относительно коэффициентов a₀ и a₁ имеет вид:

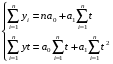
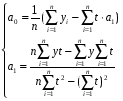и коэффициенты a₀ и a₁ равны:

Для признака x:

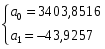
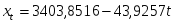
Для признака y:

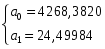
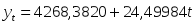
3. Изучение корреляционной зависимости между уровнями двух динамических рядов

Продолжаем рассмотрение двух выбранных нами рядов динамики. При исследовании тесноты связи между их уровнями на первое место выступает анализ смысла связи между рядами и установление факторного и результативного признаков. Без такого анализа значение коэффициента корреляции может выражать только случайное сопутствие в изменении уровней двух рядов.

Применение традиционных приемов изучения корреляции к динамическим рядам сопряжено со следующими особенностями:

1. В социально-экономических рядах динамики имеет место тенденция, вызванная действием постоянных факторов: последующие уровни рядов динамики зависят от последующих, т.е. имеется автокорреляция и авторегрессия. Это говорит о том, что нарушена одна из предпосылок применения теории корреляции - независимость отдельных наблюдений друг от друга. Если автокорреляцией при этом пренебречь, то полученная зависимость будет отражать взаимосвязь, которой в действительности не существует, или искажать реально существующую взаимосвязь.

2. Второй особенностью изучения корреляции динамических рядов является наличие временного лага, т.е. сдвига по времени изменения уровней одного ряда по отношению к изменению уровней другого ряда. Если сдвинуть уровни одного ряда относительно другого и убрать временной лаг, то получим верную оценку тесноты корреляционной связи уровней двух динамических рядов.

3. Третьей особенностью является изменение тесноты корреляционной связи уровней динамических рядов со временем.

Вначале устраняем временной лаг, значение которого определяем графически или подбором; с расчетом коэффициента корреляции.

Затем приступаем к исследованию взаимосвязи уровней. Существует четыре направления изучения корреляционной зависимости между уровнями двух динамических рядов:

- коррелирование уровней;

- коррелированно разностей;

- коррелирование остатков (отклонений от трендов);

- коррелирование с учетом фактора времени.

3.1. Изучение корреляционной зависимости между уровнями двух динамических рядов методом коррелирования уровней

Нам следует построить уравнение авторегрессии для каждого из изучаемых динамических рядов, проверив наличие временного лага:

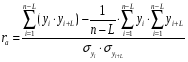
где L – величина временного лага (L=1).

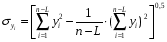
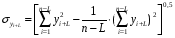
Для динамического ряда x_i:

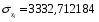
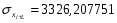
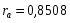
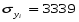Для динамического ряда y_i:

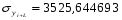
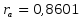
Т.к. полученные коэффициенты корреляции больше табличного, то переходим к следующему методу.

3.2. Изучение корреляционной зависимости между уровнями двух динамических рядов методом коррелирования разностей

По первоначальным динамическим рядам x_i, y_i с количеством членов n строим новые динамические ряды u_i, w_i с количеством членов n-1(табл.3.2.1), где:

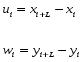
Таблица 3.2.1

u_i

w_i

640

224

336

-164

164

-276

-144

-530

-316

-410

-530

-396

-450

-44

-396

104

-84

456

104

470

416

590

470

336

550

224

336

-164

184

-276

-164

-530

-316

-470

-530

-336

-450

-44

-316

104

-164

456

104

470

416

590

470

366

Далее считаем автокорреляцию для динамических рядов u и w:

Для динамического ряда u_i:

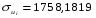
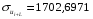
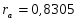
Для динамического ряда w_i:

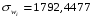
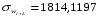
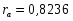
Т.к. полученные коэффициенты корреляции больше табличного, то переходим к следующему методу.

3.3.Изучение корреляционной зависимости между уровнями двух динамических рядов методом коррелирования остатков (отклонений от трендов)

В данном случае зависимость ищется в виде y_i=f(x_i), где:

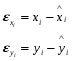
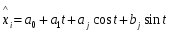
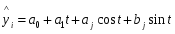
Значения 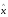и 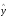представлены в табл.3.3.1:

Таблица 3.3.1

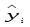
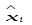
3642,182105

5521,14579

4045,276912

5549,19234

4270,521342

5237,823029

4251,468517

4673,817411

3987,065165

4011,580844

3541,933559

3431,813196

3029,073401

3093,139015

2579,614001

3089,646833

2307,713526

3425,703505

2280,001083

4014,785285

2497,741411

4702,638546

2896,496334

5308,570463

3363,373599

5673,816955

3767,245937

5704,040732

3993,851263

5394,583544

3976,378415

4831,713105

3713,351191

4169,53091

3269,023502

3588,722272

2756,179857

3248,190391

2305,945146

3242,52107

2032,68507

3576,663941

2003,392677

4164,607546

2219,755627

4852,402924

2617,70444

5459,372744

3084,562645

5826,4751

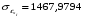Для признака x_i:

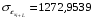
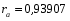
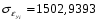Для признака y_i:

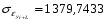
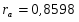
Т.к. полученные коэффициенты корреляции опять больше табличного, то переходим к следующему методу.

3.4. Изучение корреляционной зависимости между уровнями двух динамических рядов методом коррелирования с учётом фактора времени

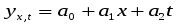Для более удобного расчёта изменяем масштаб времени, т.е. t =1. Простейшее уравнение регрессии имеет вид:

Тогда система уравнений, полученная методом наименьших квадратов имеет следующий вид:

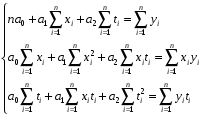
Необходимо отметить, что в этом методе коэффициент автокорреляции не исследуется.

Решение системы уравнений методом Гаусса, все необходимые данные в табл.3.4.1:

Таблица 3.4.1

t

x²

xt

yx

t²

yt

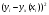
1

2

3

4

5

6

7

1

8410000

2900

14111400

1

4866

710092,7896

2

12531600

7080

18018600

4

10180

534945,7467

3

15023376

11628

19093176

9

14778

144386,4657

4

16321600

16160

18786000

16

18600

0,047492264

5

15178816

19480

16051520

25

20600

234012,5049

6

12816400

21480

13281800

36

22260

583789,6833

7

9302500

21350

10107700

49

23198

858020,2697

8

6760000

20800

8502000

64

26160

601299,3152

9

4857616

19836

7436296

81

30366

252847,3424

10

4494400

21200

8119600

100

38300

899,2211526

11

4946176

24464

9563200

121

47300

133539,1856

12

6969600

31680

12909600

144

58680

531592,5221

13

9672100

40430

16252860

169

67938

660179,6832

14

13395600

51240

19947000

196

76300

555049,3853

15

15968016

59940

21122856

225

79290

154919,9389

16

17472400

66880

20941800

256

80160

16,86990836

17

16128256

68272

17991680

289

76160

221023,9832

18

13690000

66600

14837000

324

72180

656820,769

19

10048900

60230

11646580

361

69806

832979,8976

20

7398400

54400

9873600

400

72600

580367,2874

21

5779216

50484

8976536

441

78414

278922,6984

22

5017600

49280

9385600

484

92180

267,9934274

23

5494336

53912

10923040

529

107180

143676,3624

24

7617600

66240

14490000

576

126000

551633,6354

25

10432900

80750

18139680

625

140400

732960,1726

Сумма

325

255727408

986716

350509124

5525

1453896

9954243,77

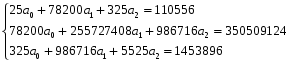
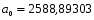
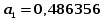
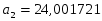
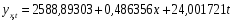
Далее определяем индекс корреляции:

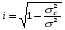
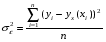
где y_x(x_i) – значение величины y, рассчитанное по уравнению регрессии при подстановке в него значений x_i и t_i; y_i – значения y из исходной таблицы.

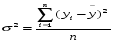
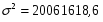
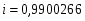
Значимость индекса корреляции определяем с помощью критерия Фишера, фактическое значение критерия Фишера равно:

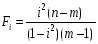
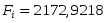
Табличное значение критерия Фишера определяем по табл.5 приложения, задаваясь уравнением значимости  и числом степеней свободы k₁=m-1; k₂=n-m.

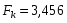
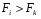
Если то величину индекса корреляции считаем значимой.

Определим коэффициент детерминации:

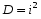
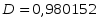
Следовательно, величина y зависит от величин x и t на 98,01%. Остальные 1,99% - это зависимость величины y от неучтённых величин.

Подводя итог необходимо отметить, что в исследовании методом коррелирования динамических рядов, с учётом фактора времени была определена весьма высокая теснота связи, равная 0,9900; величина коэффициента детерминации равная 0,9801 говорит о том, что величина y зависит от величин x и t, включённых в уравнение, на 98,01%, все остальные 1,99% - это зависимость величины y от неучтённых величин.