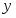
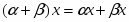Содержание.

Введение……………………………………………………………………….2

Глава I. Нормированные пространства…………………………………..3

§1. Понятие нормированного пространства........................................3

§2. Пространства суммируемых функций…………………………...5

§3. Интеграл Лебега – Стилтьеса………………………………..........7

Глава II. Интерполяция в пространствах суммируемых функций….11

§1. Теорема Марцинкевича и ее применение……………………...11

§2.Теорема Рисса–Торина и ее применение ………………………15

Глава III. Пространства суммируемых последовательностей…..…....24

§1. Основные понятия……………………………………………….24

§2. Связь между коэффициентами Фурье 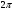-периодической функции и ее нормой в 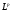…………….……………………………25

Литература………………………………………………………………...28

Введение.

Понятие нормированного пространства – одно из самых основных понятий функционального анализа. Теория нормированных пространств была построена, главным образом, С.Банахом в 20-х годах 20 века. В работе эта теория прилагается к изучению суммируемых функций и последовательностей с позиций функционального анализа. Эти функции и последовательности образуют нормированные пространства, на которых вводятся операции сложения и умножения на число, а также норма.

Основным объектом классического функционального анализа являются операторы, действующие из одного банахова пространства в другое.

Целью данной работы является рассмотрение линейных операторов, действующих из одного пространства суммируемых функций в другое, а также в пространство суммируемых последовательностей.

Основные понятия нормированных пространств изложены в первой главе.

Вторая глава посвящена интерполяции в пространствах измеримых функций. Рассмотрена теорема Марцинкевича, являющаяся одной из классических в теории интерполяции, и дано ее подробное доказательство. Приводится доказательство непрерывности оператора свертки с использованием данной теоремы. Также рассмотрена интерполяционная теорема Рисса – Торина и ее применение.

В третьей главе даны основные понятия пространства суммируемых последовательностей, доказана связь между коэффициентами Фурье 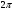- периодической функции и ее нормой в 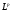при помощи теоремы Марцинкевича.

Глава I. Нормированные пространства.

§1. Понятие нормированного пространства.

Введем основные понятия теории нормированных пространств.

Определение. Непустое множество 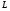называется линейным пространством, если оно удовлетворяет следующим условиям:

Ι. Для любых двух элементов 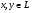однозначно определен элемент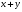, называемый их суммой, причем

1. 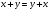(коммутативность)

2. 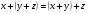(ассоциативность)

3. В существует такой элемент 0, что для всех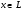

4. Для каждого 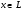существует такой элемент 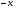, что .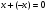

II. Для любого числа и любого элемента 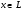определен элемент 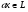, причем

5.

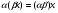
6.

III. Операции сложения и умножения связаны между собой дистрибутивными законами:

7.

8.

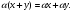
Определение. Линейное пространство 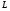называется нормированным, если на нем задана неотрицательная функция 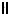, называемая нормой, удовлетворяющая условиям:

1. ;

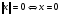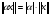2. для любого 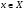и любого числа ;

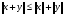3. для любых 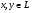(неравенство треугольника).

Определение. Оператором называется отображени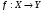е , где 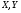- это линейные пространства.

Определение. Оператор 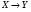называется линейным, если для любых элементов 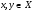и любых чисел 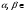R выполняется равенство:

.

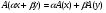Определение. Пусть 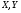- линейные нормированные пространства,

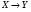– линейный оператор,.

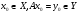Линейный оператор непрерывен в точке 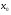, если из того, что 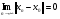следует, что .

Определение. Линейный оператор 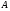непрерывен, если он непрерывен в каждой точке .

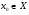Определение. Линейный оператор называется ограниченным, если .

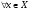
Утверждение. Для линейного нормированного пространства непрерывность линейного оператора равносильна его ограниченности.

Определение. Наименьшая из констант M таких, что 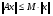, называется нормой оператора А и обозначается .

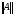В частности, выполняется .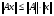

Справедливо следующее утверждение: для любого ограниченного линейного оператора .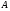

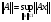§2. Пространства суммируемых функций.

Среди различных классов нормированных пространств, встречающихся в анализе, один из важнейших - это пространство суммируемых функций. Далее будем рассматривать именно эти нормированные пространства.

Определение. Пусть 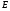– некоторое фиксированное измеримое множество из 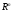. Пространством 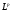, где , называется нормированное пространство, элементами которого служат функции 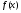, измеримые и почти всюду конечные на 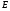, для которых выполняется

Функции, эквивалентные друг другу на 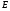, не различаются, а считаются за один и тот же элемент пространства 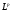. В частности, нулевой элемент в 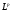– это совокупность всех функций, равных нулю почти всюду.

Сложение элементов в 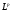и умножение их на числа определяются как обычные сложение и умножение функций. Точнее, поскольку каждый элемент в 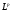– это класс эквивалентных между собой функций, то для того, чтобы сложить два таких класса, нужно брать в них по представителю и потом суммой этих классов называют класс, содержащий сумму выбранных представителей. Результат не будет зависеть от выбора представителей в данных классах.

Определение. Число называется нормой функции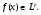

Будут выполняться все свойства нормы:

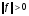1. и 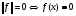почти всюду;

2. 

3. 

Первое свойство cледует из определения нормы и того, что

Второе – из свойства интеграла: постоянный множитель можно выносить за знак интеграла. Третье свойство вытекает из неравенства Минковского: для любых функций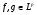

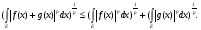
Определение. Функция 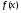называется ограниченной почти всюду, если существует неотрицательное число такое, что почти всюду выполняется неравенство . (*)

Определение. Пространством называется нормированное пространство, элементами которого служат почти всюду ограниченные функции 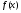. Нормой называется наименьшая из констант, удовлетворяющих неравенству (*).

Для выполняется почти всюду неравенство .

Через 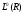будем обозначать линейное пространство измеримых функций, заданных на R.

Среди линейных операторов, действующих в пространстве 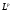, рассмотрим следующие.

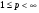Определение. Оператор , действующий из пространства () в 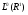, называется оператором слабого типа (p,p), если

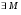
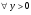
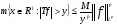, где 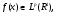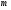- мера множества, и оператором типа (p,p), если .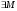

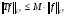По определению оператор типа 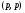является ограниченным, что равносильно его непрерывности.

Предложение 1. Любой оператор типа 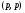есть оператор слабого типа .

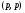Доказательство.

Нужно доказать, что .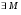

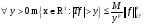Воспользуемся неравенством Чебышева: .

Возьмем любое положительное число 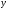. По неравенству Чебышева

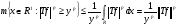. Но по условию .

Учитывая последнее соотношение, имеем 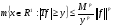, что и требовалось доказать.

§3. Интеграл Лебега – Стилтьеса.

Далее понадобится понятие интеграла Лебега – Стилтьеса. Введем это понятие.

Определение. Пусть на R задана монотонно неубывающая функция , которую для определенности будем считать непрерывной слева. Определим меры всех сегментов, интервалов и полусегментов равенствами

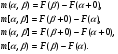
Таким образом, функция 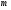, которая каждому сегменту ставит в соответствие меру этого сегмента, будет:

1. принимать действительные неотрицательные значения;

2. аддитивной, т.е. мера объединения есть сумма мер этих сегментов.

Применив стандартное распространение меры, получим меру на некоторой 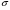- алгебре.

Определение. Меру 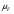_, получающуюся с помощью такого построения, называют мерой Лебега – Стилтьеса, отвечающей функции , а саму функцию называют производящей функцией этой меры.

Определение. Пусть 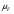- мера на R, порожденная монотонной функции . Для этой меры обычным образом определяется класс суммируемых функций и вводится понятие интеграла Лебега .

Такой интеграл, взятый по мере 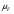, отвечающей производящей функции , называется интегралом Лебега – Стилтьеса и обозначается .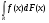

Теперь докажем факт, который используется при доказательстве интерполяционной теоремы.

Предложение 2. 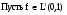и для

и 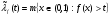, тогда

(1) 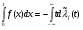, и если 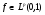, и , то

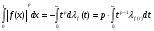. (2)

Доказательство.

Равенство (1) следует из определения интегралов Лебега и Лебега – Стилтьеса:

Если 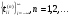- последовательность разбиений действительной ос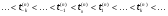и:

, и 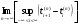, то интегралы 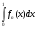, где 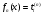, если 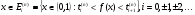, стремятся при .

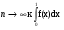С другой стороны:

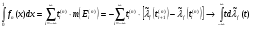при .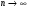

Это и доказывает равенство (1).

Пусть теперь 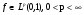. По (1), учитывая, что , получаем 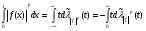(2’)

При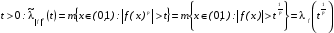

Следовательно, из соотношения (2’), делая замену переменных 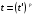, получим первое равенство (2).

Далее, для любого 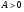выполняется

(интегрирование по частям: ).

Для доказательства второго равенства в (2) достаточно устремить в последнем соотношении число 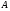к 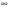и использовать оценку:

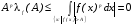при.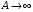

Предложение 2 доказано.

Замечание. Если функция 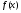задана на 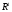, то, применяя равенство (2) для функции 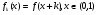, , 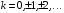и учитывая, что 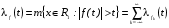, получим

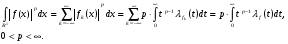(3)

Глава II. Интерполяция в пространствах суммируемых функций.

§1. Теорема Марцинкевича и ее применение.

Одной из важнейших в теории интерполяции является теорема Ж.Марцинкевича, доказанная им в 1939 году. Прежде чем рассмотреть теорему, докажем предложение.

Пусть дана функция 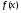. Положим для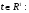

, .

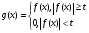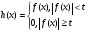Предложение 3. Пусть 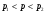, , 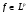для любого положительного числа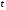 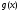и 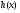– функции, описанные выше. Тогда .

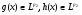Доказательство.

g(x)

f(x)

t

h(x)

Нужно показать, что 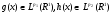, т.е. .

I. Для функции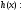

1) если 0<t , то , т.к.

2) Пусть t>1.

Обозначим , .

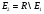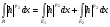. Конечность 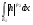доказана в первом случае. Рассмотрим второй интеграл.

Покажем, что 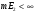. Предположим противное, что .

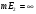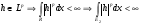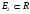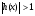, т.к. . С другой стороны, . Но на 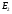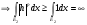, т.е. 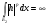, а это противоречие. Получили, что 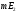конечна и т.к. интеграл от ограниченной функции по конечной мере конечен, то 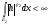. Тогда .

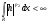II.для функции :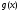

1) если 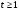, то .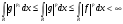

2) Пусть .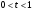

Пусть

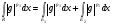. Конечность 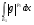доказана в первом случае. Нужно показать, что конечен.

Докажем, что 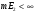. Предположим противное, что .

().

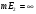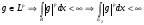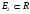С другой стороны 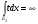. Но 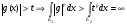, т.е.

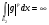. Пришли к противоречию.

Получили, что 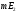конечна и т.к. интеграл от ограниченной функции по конечной мере конечен, то 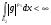. Следовательно, . Предложение доказано.

Следствие. Для всех 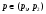справедливо включение: .

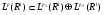Замечание 2. Пусть оператор задан на пространстве 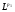и на 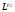. Тогда оператор можно распространить с сохранением линейности до оператора, действующего из пространства

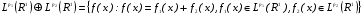т.е.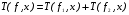 для любой функции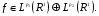

Такое определение функции 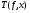не зависит от выбора 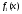и Действительно. Возьмем другое представление функции :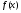

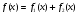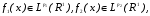, где т.е.

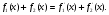Нужно доказать, что .

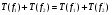Из условия следует 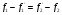. Левая часть равенства – это функция из 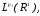правая часть - из 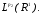Применим к равенству оператор T:

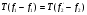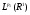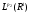. Так как T линеен в пространствах и , то 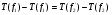. Отсюда 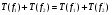, что и требовалось доказать.

Теорема Марцинкевича. Если линейный оператор Т имеет слабый тип 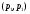и одновременно слабый тип 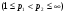, то Т имеет тип 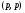для любого из интервала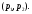

Доказательство.

Считаем, что 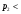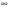. Фиксируем функцию 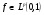и положительное число 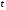. Оценим величину

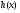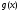Пусть и функции, описанные выше.

Тогда 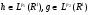и по замечанию 2.

Следовательно, .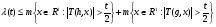

Используя оценки слабого типа 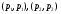, находим, что при положительном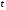

.

Из последнего неравенства и формулы (3) из замечания 1 получаем

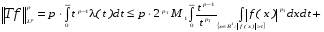
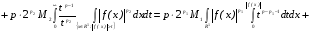
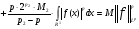, т.е. оператор Т имеет тип 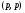. Теорема доказана.

В качестве применения этой теоремы рассмотрим следующий пример.

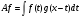Утверждение 2. Пусть . Тогда оператор будет непрерывным оператором в пространстве , .

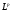Доказательство.

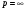Рассмотрим два случая, когда и . Докажем, что оператор 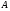является оператором типа 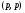для этих случаев. Тогда по предложению 1 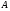будет оператором слабого типа 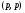для и 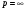. Применив интерполяционную теорему Марцинкевича, получим, что – оператор типа для любого 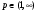, а это равносильно его непрерывности.

1. и 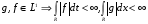. Докажем, что найдется число , такое, что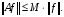

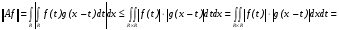
Учитывая последнее равенство и то, что для любого действительного числа 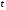верно 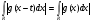, получим

, где .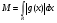

2).

Нужно доказать, что

Для 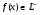почти всюду выполняется неравенство: . (*)

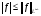Обозначим , .

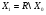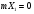. Так как , то .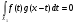

Исходя из последнего соотношения и неравенства (*), получаем

.

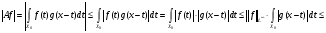
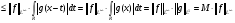Таким образом, доказали, что оператор свертки 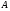непрерывен в пространстве 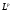для любого р1.

§2. Интерполяционная теорема Рисса – Торина

и ее применение.

Прежде чем рассмотреть теорему Рисса – Торина и ее приложение, приведем определения и докажем факты, связанные с теорией банаховых пространств, которые понадобятся для этого.

Определение. Последовательность 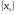метрического пространства Х называется фундаментальной, если .

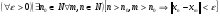Верно следующее утверждение.

Утверждение. Если последовательность 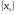сходится, то она фундаментальная.

Обратно верно не всегда.

Определение. Метрическое пространство называется полным, если в нем любая фундаментальная последовательность сходится.

Определение. Если пространство , порожденное нормой, является полным, то линейное нормированное пространство называется банаховым.

Определение. Пусть – банахово пространство, 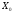– подпространство в . 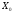называется всюду плотным в Х, если 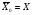, т.е.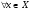 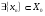, такая, что .

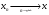Утверждение 4 . Пусть оператор 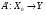, где 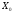плотно в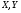– банахово пространство. Тогда оператор 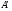можно распространить на , т.е. существует оператор 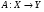, такой, что 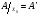и .

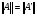Доказательство.

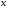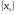Возьмем из . По определению существует последовательность из 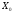такая, что 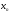стремится к 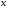, при 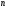стремящемся к .

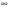Докажем, что из 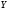будет фундаментальной последовательностью. Тогда, т.к. 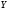полное, последовательность будет сходящейся.

Возьмем произвольное положительное число . Найдем номер 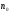, для которого выполняется 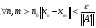.Тогда

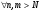
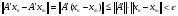. Следовательно, последовательность фундаментальная.

Пусть стремится к 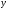. Определим оператор 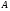равенством .

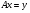а) Проверим корректность определения оператора .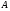

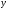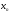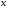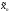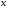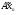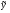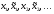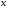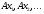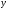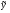Итак, стремится к , стремится к . Возьмем другую последовательность , имеющую в пределе . Тогда будет стремится к некоторому элементу .Составим новую последовательность Ее пределом будет . Пусть соответствующая последовательность стремится к . Из последней можно выбрать две подпоследовательности и , сходящиеся соответственно к и .Следовательно, 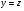и 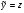, т.е. и 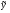совпадают.

б) Докажем линейность оператора А. Пусть 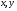Х; 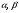- произвольные числа. Рассмотрим элемент 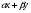. По определению существуют последовательности {x_n},{y_n}, такие, что 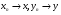. Тогда .

.

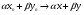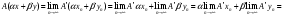
Получили , что и означает по определению линейность оператора А. При этом, т.к. если 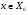, то в качестве 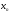можно взять 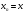для всех n. Тогда 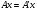и .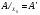

в) Докажем непрерывность оператора А.

Возьмем . , .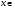

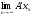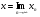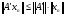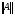. По теореме о предельном переходе в неравенстве будет выполняться неравенство . Т.к. по определению - это наименьшая из констант, удовлетворяющих данному неравенству, то . (*)

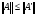С другой стороны, по определению 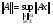, 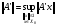. Так как , то . (**)

Учитывая неравенства (*) и (**) , установили равенство 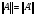. Таким образом, утверждение доказано.

Определение. Функция 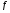называется простой, если она представляет собой конечную линейную комбинацию характеристических функций попарно непересекающихся измеримых множеств 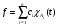, где .

Теорема Лебега. Если последовательность 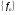на 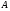сходится к 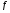и при всех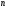 , где 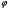суммируема на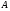, то предельная функция 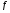суммируема на 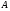и .

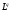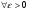
Предложение 4. Множество простых функций всюду плотно в , т.е. 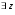, такая, что 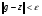,где – простая функция.

Доказательство.

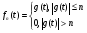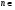I.Обозначим , где N.

g(t)

n

-n

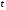
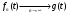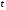Ясно, что для почти всех . Тогда для почти всех . Следовательно, .

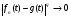С другой стороны, (*) 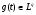,т.е. 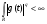. Поэтому 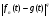суммируема. Применим теорему Лебега к неравенству (*) :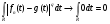. Получим, что 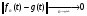и, значит, приблизили функциями . Возьмем произвольное положительное число . Найдем функцию такую, что .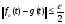

II. Приблизим 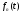ступенчатой функцией.

Обозначим 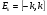, где 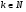. Положим .

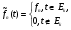По свойству интеграла Лебега для любого положительного найдется 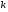, такое, что 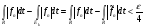. Это означает, что .

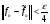Отрезок 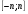разобьем на 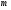равных частей точками 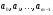так, чтобы .

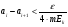Обозначим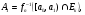

.

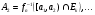
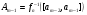Рассмотрим функцию 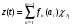. Тогда 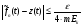. Следовательно, 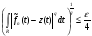, т.е. .

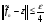В результате нашлась простая функция такая, что

.

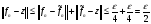III. Таким образом, 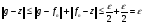. Предложение доказано.

Первая интерполяционная теорема в теории операторов была получена М.Риссом в 1926 году в виде некоторого неравенства для билинейных форм. Ее уточнение и операторная формулировка были даны Г.О.Ториным. Вся теория интерполяции линейных операторов первоначально развивалась в направлении обобщения этой теоремы. Дадим ее формулировку.

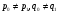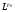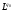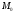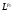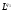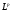Теорема. Пусть . Оператор Т действует из пространства в с нормой и одновременно из в с нормой .Тогда Т будет непрерывным оператором из пространства в 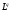с нормой , удовлетворяющей неравенству 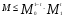при условии, что 0<t<1 и ; .

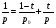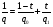Теперь рассмотрим приложение теоремы Рисса – Торина в доказательстве следующего факта.

Теорема. Пусть 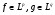и для чисел 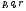выполняется равенство 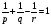.Тогда свертка .

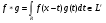Доказательство.

Нужно доказать, что 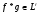, т.е. 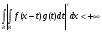. Зафиксируем произвольную функцию 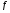из 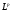. Докажем сначала требуемый результат для частного случая, когда функция g простая, а затем распространим на произвольные функции g.

I. Пусть функция 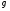простая.

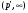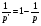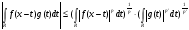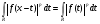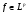1) Рассмотрим оператор свертки на множестве простых функций и проверим, что он типа , где . В силу неравенства Гельдера . Учитывая геометрический смысл интеграла, получим для любого действительного числа х. Тогда . Так как , то 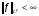, т.е. равна некоторому числу 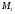. Таким образом, 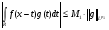. Следовательно, нашлась константа , такая, что 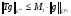. Это и означает, что оператор свертки Т на множестве простых функций типа .

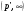2) Проверим, что оператор Т типа 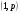, т.е. .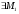

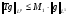Рассмотрим случай, когда функция g имеет вид: .

.

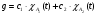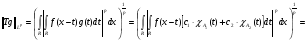
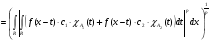Обозначим .

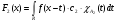Тогда правая часть равенства примет вид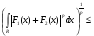

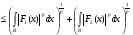
по неравенству Минковского. (1)

Рассмотрим первое слагаемое

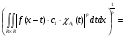
(2) Аналогично второе слагаемое

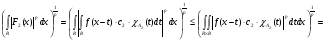
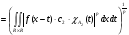
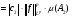. (3)

Таким образом, учитывая (1),(2),(3), получим 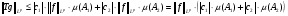. Найдем

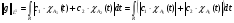, т.к. .

Далее имеем

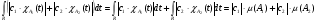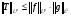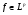. В результате, ,т.к. , то 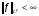и равна некоторому числу.

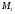Совершенно аналогично доказывается 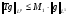для случая, когда .

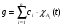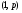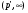1) Таким образом, из пунктов I.1 и I.2 получим, что типа и , и,

следовательно, будет типа 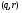при условии 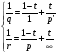, где .

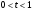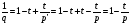; , т.е. 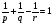, что и дано по условию.

Таким образом, применив теорему Рисса – Торина, установили истинность доказываемого утверждения для всех простых функций .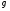

II. Пусть 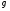– произвольная функция из .

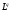По предложению 4 множество простых функций всюду плотно в .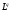

По утверждению 4 оператор свертки можно распространить на 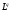и тогда доказываемый факт верен для любой функции 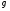из 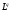. Теорема доказана.

Глава III. Пространства суммируемых последовательностей.

§1. Основные понятия.

Рассмотрим применение теории интерполяции для пространств .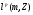

Пусть {_z}_zZ - последовательность неотрицательных чисел. Определим на множестве Z меру следующим образом: 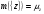для любого целого числа . Пространство суммируемых со степенью p последовательностей относительно меры m, то есть таких, что 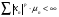обозначается .

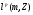Так как мера m определена на множестве всех подмножеств множества Z, то любую последовательность можно рассматривать как измеримую функцию. Обозначим через 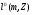линейное пространство всех последовательностей.

Определение. Число 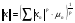называется нормой последовательности x_n из l^p(m,Z).

В случае, если 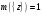для всех z, то получим классическое пространство l^p(Z) последовательностей, суммируемых со степенью p .

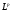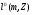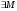
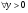
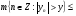
Определение. Оператор Т, действующий из пространства в называется оператором слабого типа (p,p), если 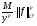, где 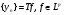, и оператором типа (p,p), если .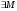

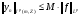В этом случае остается справедливым следующий факт: любой оператор типа 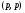есть оператор слабого типа 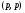. Прежде чем установить его истинность, докажем утверждение, которое для этого понадобится.

Утверждение 5. Пусть дана последовательность из 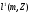с неотрицательными членами. Тогда .

Доказательство.

Обозначим 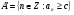. Нужно доказать, что .

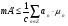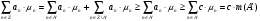. Получили, что .

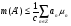Утверждение доказано.

Предложение 5. Любой оператор типа 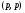есть оператор слабого типа .

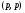Доказательство.

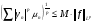Дано, что и . Доказать, что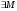

.

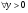
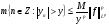Возьмем произвольное положительное число 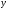. По утверждению 5

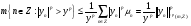. По условию 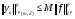. Тогда 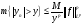, что и требовалось доказать.

Легко увидеть, что теорема Марцинкевича будет справедлива и для операторов, действующих из пространств 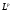в пространство .

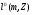§2. Связь между коэффициентами Фурье 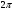- периодической функции и ее нормой в .

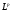Теория интерполяции имеет многочисленные приложения в теории рядов Фурье.

Определение. Пусть 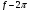-периодическая функция, такая что 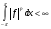. Нормой 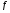в пространстве называется число 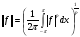, а коэффициентами Фурье функции 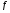называются числа .

Для функций 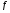из пространства выполняется равенство .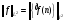

В случае других значений это, вообще говоря, не верно. Однако можно указать следующую оценку.

Предложение 6. Пусть 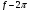периодическая функция из 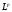. Тогда для любого числа из отрезка [1,2] существует константа 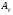, такая, что .

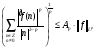Доказательство.

Рассмотрим оператор 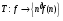и определим меру 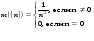, т.е. оператор действует из 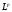в .

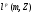1. Докажем, что оператор слабого типа : .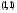

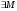
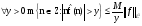Зафиксируем произвольное положительное число .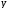

.

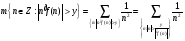Пусть 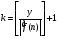. Тогда 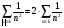. (2)

Далее имеем

.

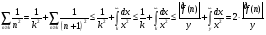Учитывая равенства (1) и (2), получим, что .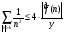

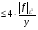В результате нашли константу , такую, что .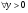

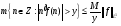2) Докажем, что типа : .

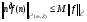Уже говорилось, что для функций из пространства выполняется равенство 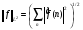. (3)

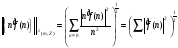. По неравенству (3) 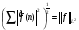. По предложению 5 оператор будет слабого типа .

3) По теореме Марцинкевича будет типа 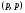для любого из интервала (1,2), т.е. 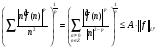, что и требовалось доказать.

Литература.

1. Вулих Б.З. Краткий курс теории функций вещественной переменной. «Наука», Москва, 1965.

2. Кашин Б.С., Саакян А.А. Ортогональные ряды. «Наука», Москва, 1984.

3. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. «Наука», Москва, 1968.

4. Крейн С.Г., Петунин Ю.И., Семенов Е.М. Интерполяция линейных операторов.«Наука», Москва, 1978.

5. Натансон И.П. Теория функций вещественной переменной. «Наука», Москва, 1974.

Распространим меру с сохранением свойств 1 и 2, определенную пока для сегментов, на более широкий класс множеств – так называемые элементарные множества.

Назовем множество элементарным, если его можно представить хотя бы одним способом как объединение конечного числа попарно непересекающихся сегментов.

Определим теперь меру 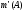для элементарных множеств следующим образом: если 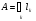, где 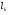- попарно непересекающиеся сегменты, то .

Далее распространим меру и на бесконечные объединения сегментов. Для того, чтобы при этом не встречались множества «бесконечной меры», ограничимся рассмотрением множеств, целиком принадлежащих отрезку 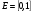. На совокупности всех таких множеств определим две функци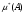и и :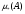

Определение. Верхней мерой 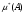множества 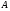называется число, где нижняя грань берется по всевозможным покрытиям множества А конечными или счетными системами сегментов.

Определение. Нижней мерой 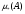множества 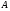называется число .

Определение. Множество 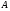называется измеримым, если 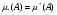. Их общее значение 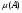называется лебеговской мерой.

Итак, распространили меру с элементарных множеств на более широкий класс множеств, называемых измеримыми, замкнутый относительно операций взятия счетных сумм и пересечений. Построенная мера является на этом классе множеств 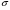- аддитивной, т.е. если - последовательность попарно непересекающихся измеримых множеств и 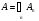, то .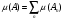

Однако, мы рассмотрели лишь те множества, которые являются подмножествами .

Нетрудно освободиться и от этого ограничения. Представив всю числовую ось как сумму отрезков 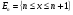( 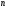- целое), будем говорить, что множество 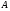измеримо, если его пересечение 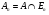с каждым из этих отрезков измеримо, и ряд 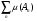сходится. При этом положим по определению, .

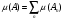Причем совокупность множеств, измеримых относительно данной меры, также будет замкнута относительно операций взятия счетных сумм и пересечений, а мера будет 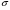- аддитивна.

Определение. Меру 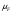, получающаяся с помощью такого построения, называют мерой Лебега – Стилтьеса, отвечающей функции , а саму функцию называют производящей функцией этой меры.

32