ГОУ ВПО

ДАЛЬНЕВОСТОЧНЫЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

кафедра

«Управление

эксплуатационной работой»

Расчетно-графическая работа

«Обработка статистических данных и

установление закона распределения

случайных величин»

Выполнил: Роднов Е.А.

студент 232 группы

Проверил: Виноградова Л.Л.

Хабаровск, 2007

В табл. 1 приведены моменты фактического прибытия поездов на станцию, полученные в результате натурных наблюдений.

Необходимо:

1. Составить статистический ряд интервалов прибытия грузовых поездов на сортировочную станцию.

2. Установить основные временные параметры входящего на станцию поездопотока (среднее значение, дисперсию, среднее квадратическое отклонение и коэффициент вариации).

3. Построить гистограмму распределения вероятностей появления интервалов между поездами.

4. Определить параметр в эрланговском распределении интервалов прибытия поездов в парк приема.

5. По внешнему виду гистограммы подобрать теоретический закон распределения.

6. Проверить по критерию согласия Пирсона и условию Романовского правдоподобность гипотезы о выбранном теоретическом распределении интервалов прибытия поездов в расформирование.

7. Рассчитать число бригад ПТО в парке приема (время на техническое обслуживание t_то принять равным 20 мин).

Таблица 1

Моменты фактического прибытия поездов на станцию

№ п/п

Время прибытия (ч, мин)

№ п/п

Время прибытия (ч, мин)

№ п/п

Время прибытия (ч, мин)

№ п/п

Время прибытия (ч, мин)

№ п/п

Время прибытия (ч, мин)

1

0-04

19

6-01

37

12-43

55

20-45

73

4-02

2

0-10

20

6-26

38

13-00

56

22-45

74

4-20

3

0-25

21

7-12

39

14-10

57

22-49

75

4-30

4

0-45

22

7-22

40

14-22

58

22-54

76

4-55

5

1-15

23

7-40

41

14-24

59

22-59

77

5-08

6

1-30

24

8-01

42

14-50

60

23-15

78

5-15

7

2-01

25

8-15

43

14-55

61

23-25

79

5-22

8

2-26

26

9-35

44

16-25

62

23-47

80

6-15

9

2-40

27

9-45

45

16-35

63

23-51

81

7-05

10

2-45

28

9-53

46

16-38

64

0-04

82

7-25

11

2-50

29

10-05

47

16-50

65

0-35

83

7-35

12

3-48

30

10-15

48

17-40

66

0-48

84

7-44

13

3-52

31

10-26

49

18-05

67

1-01

85

8-10

14

3-58

32

10-34

50

18-10

68

1-48

86

8-21

15

4-15

33

11-05

51

18-36

69

2-38

87

8-27

16

4-40

34

11-37

52

18-50

70

3-01

88

8-38

17

5-09

35

12-04

53

19-58

71

3-12

89

10-00

18

5-43

36

12-20

54

20-11

72

3-50

Решение

Интервалы прибытия определил путем вычитания предыдущего времени прибытия поезда из последующего и представил в табл. 2.

Таблица 2

Интервалы прибытия поездов

№ п/п

Интервал, мин

№ п/п

Интервал, мин

№ п/п

Интервал, мин

№ п/п

Интервал, мин

№ п/п

Интервал, мин

№ п/п

Интервал, мин

№ п/п

Интервал, мин

№ п/п

Интервал, мин

№ п/п

Интервал, мин

1

6

11

58

21

10

31

8

41

26

51

14

61

22

71

38

81

20

2

15

12

4

22

18

32

31

42

5

52

68

62

4

72

12

82

10

3

20

13

6

23

21

33

32

43

90

53

13

63

13

73

18

83

9

4

30

14

17

24

14

34

27

44

10

54

34

64

31

74

10

84

26

5

15

15

25

25

80

35

16

45

3

55

120

65

13

75

25

85

11

6

31

16

29

26

10

36

23

46

12

56

4

66

13

76

13

86

6

7

25

17

34

27

8

37

17

47

50

57

5

67

47

77

7

87

11

8

14

18

18

28

12

38

70

48

25

58

5

68

50

78

7

88

82

9

5

19

25

29

10

39

12

49

5

59

16

69

23

79

53

10

5

20

46

30

11

40

2

50

26

60

10

70

11

80

50

Группировка происходит по классам (разрядам). Количество классов К определил по формуле:

К = (1 + 3,21 ∙ lg n), (1)

где n – общее число наблюдений.

К = (1 + 3,21 ∙ lg 88) = 7, 24.

Принимаем количество классов К равным 8.

Величину интервала (шаг класса) группирования I определил по формуле:

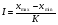, (2)

где х_max, х_min – наибольшее и наименьшее значения случайной величины.

.

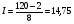Далее произвел группирование интервалов по разрядам. В процессе группирования установил, сколько интервалов m_i попало в разряд t_i – t_i+1. Последующие расчеты основных параметров статистического ряда выполнил в форме табл. 3, в которую свел все промежуточные результаты вычислений.

Таблица 3

Обработка статистического ряда интервалов между моментами

прибытия поездов на станцию

№ п/п

Границы разрядов, t_i - t_i+1

Число интервалов в разряде, m_i

ЧастостьP_i

Среднее значение в разряде, t_i

t_i ∙ P

t_i² ∙ P

1

2-16,75

46

0,523

9,375

4,901

45,943

2

16,75-31,5

25

0,284

24,125

6,854

165,345

3

31,5-46,25

5

0,057

38,875

2,209

85,867

4

46,25-61

6

0,068

53,625

3,656

196,066

5

61-75,75

2

0,023

68,375

1,554

106,253

6

75,75-90,5

3

0,034

83,125

2,834

235,560

7

90,5-105,25

0

0

97,875

0

0

8

105,25-120

1

0,011

112,625

1,280

144,141

Итого

 

88

1

 

23,287

979,176

Для каждого разряда наблюдаемых величин подсчитал их количество и определил частость.

Математическое ожидание М (х) определил по формуле:

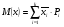, (3)

где 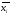– среднее значение разряда i.

М (х) = 9,375 ∙ 0,523 + 24,125 ∙ 0,284 + 38,875 ∙ 0,057 + 53,625 ∙ 0,068 + 68,375 ∙ 0,023 + 83,125 ∙ 0,034 + 97,875 ∙ 0 + 112,625 ∙ 0,011 = 23,287.

Дисперсию D (x) определил по формуле:

D (x) = M² (x) – (M[x])², (4)

где 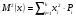– второй начальный момент случайной величины.

M² (x) = 9,375² ∙ 0,523 + 24,125² ∙ 0,284 + 38,875² ∙ 0,057 + 53,625² ∙ 0,068 + 68,375² ∙ 0,023 + 83,125² ∙ 0,034 + 97,875² ∙ 0 + 112,625² ∙ 0,011 = 979,176.

D (x) = 979,176 – 23,287² = 436,892.

Среднее квадратическое отклонение 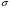– это квадратный корень из дисперсии:

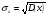. (5)

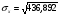= 20,902.

Коэффициент вариации 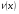определяется как отношение среднего квадратического отклонение к математическому ожиданию:

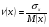. (6)

.

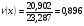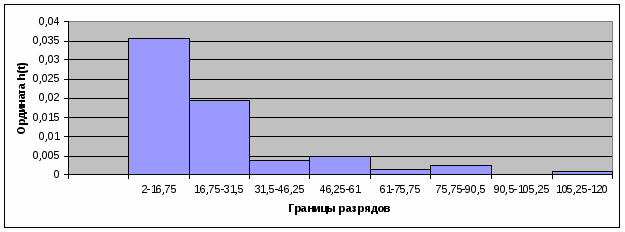
На основании расчетных характеристик (табл. 3) строится гистограмма распределения интервалов прибытия поездов (рис. 1).

Ординату гистограммы определил по формуле:

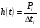, (7)

где ∆t_i = t_i+1 – t_i шаг конкретного i-го разряда.

Рис. 1. Гистограмма распределения интервалов прибытия поездов

Параметр Эрланга определил по следующей формуле:

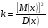, (8)

.

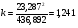Исходя из найденного значения параметра Эрланга и внешнего вида гистограммы, сделал предположение, что для данного распределения наиболее близок закон показательного теоретического распределения.

Теоретическая вероятность Р*_i интервалов определенной величины в их общей совокупности равна:

Р*_i = F(t_i) – F(t_i–1), (9)

где F(t_i) и F(t_i–1) – функция показательного распределения.

F(t_i) = 1 – е^–λti,

F(t_i–1) = 1 – е^–λti–1,

где λ – интенсивность поступления поездов на станцию

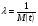. (10)

.

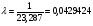Рассчитанные данные занесены в табл. 4.

Таблица 4

Характеристики распределения интервалов

между поступающими в переработку поездами

Границы разрядов, t_i - t_i+1

Число интервалов в разряде, m_i

λt

е^–λt

F(t_i)

Р*_i

nР*_i

m_i–nP*_i

(m_i–nP*_i)²

(m_i–nP*_i)²/nР*_i

2-16,75

46

0,086

0,918

0,082

0,429

37,731

8,269

68,376

1,8122

16,75-31,5

25

0,719

0,489

0,511

0,229

20,113

4,887

23,885

1,1875

31,5-46,25

5

1,353

0,261

0,739

0,122

10,721

-5,721

32,733

3,0531

46,25-61

6

1,986

0,139

0,861

0,065

5,715

0,285

0,081

0,0142

61-75,75

2

2,619

0,074

0,926

0,035

3,046

-1,046

1,095

0,3595

75,75-90,5

3

3,253

0,040

0,960

0,018

1,624

1,376

1,894

1,1660

90,5-105,25

0

3,886

0,021

0,979

0,010

0,866

-0,866

0,749

0,8657

105,25-120

1

4,520

0,011

0,989

0,005

0,461

0,539

0,290

0,6286

5,153

0,006

0,994

88

9,0867

Как видно из последней графы табл. 4 критерий согласия Пирсона χ² = 9,0867.

Число степеней свободы r определил по формуле:

r = R – S, (11)

где R – число разрядов; S – число наложенных связей.

r = 8 – 2 = 6.

Пользуясь специальной таблицей, определяется вероятность Р(χ²) = 0,1736. Значит, гипотеза о показательном распределении интервалов поступления поездов на станцию не совсем правдоподобна.

По условию Романовского, гипотеза о принятом теоретическом законе распределения считается правдоподобной, если соблюдается следующее неравенство:

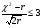. (12)

, следовательно, расхождение между теоретическим и эмпирическим распределениями не столь существенно и гипотеза о показательном законе распределения интервала прибытия поездов на станцию правдоподобна.

Число бригад ПТО в парке приема рассчитал, исходя из условия:

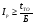, (13)

где I_p – расчетный интервал прибытия поездов; t_ТО – время на техническое обслуживание поезда одной бригадой; Б – число бригад.

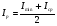, (14)

где I_min – минимальный интервал между поездами, прибывающими на станцию, I_min = 2 мин.

I_cp = M(t) = 23, 287.

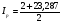= 12,64 мин.

Время на техническое обслуживание t_ТО принимается равным 20 мин.

Число бригад рассчитал из формулы (13) и округлил до целого числа, следовательно, принял 2 бригады ПТО.