Общие свойства конечных групп с условием плотности для F субнормальных подгрупп
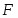
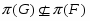







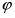





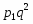


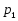
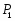
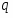
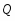
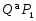
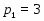
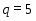
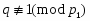
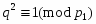
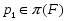
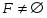
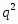
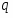
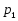
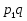
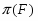
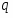
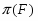
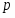



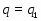

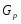
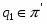
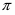

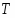
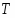
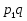
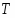

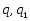
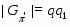

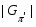
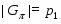

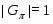
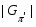
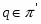
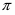



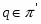
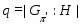
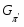


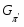
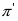
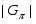
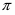

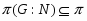
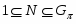
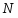


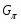

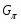
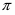
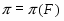

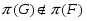

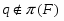
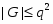
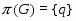
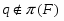
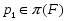

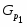
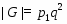
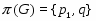
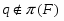
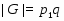
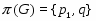

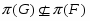





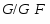
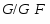
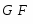
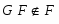
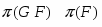
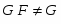



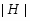
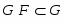
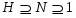
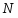








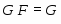
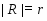
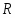
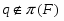
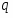
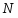
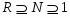
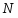

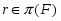

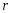
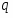

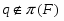
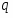
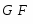
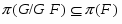

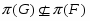

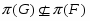





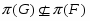
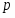




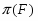
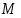

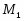



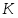
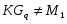
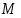
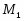
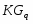
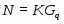
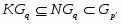
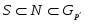
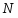




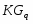


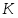

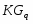

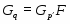
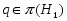
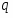
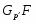




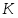

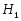



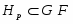
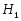


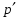

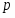
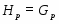
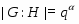


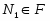
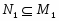
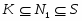





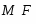
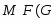
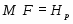
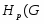
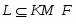
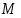
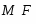
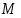
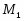
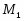
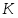
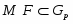
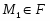
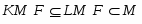
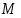


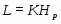

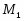
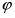
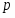
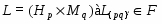
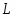
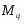
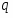
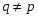
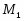
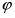
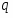
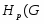
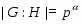


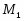
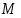
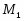

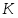
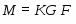
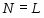
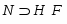
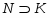
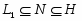
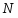



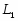
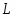
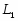

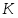
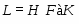
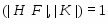







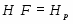
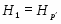
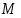

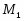
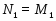


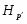
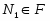
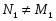
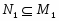
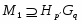
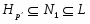
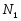


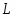
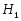


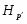
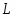
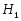
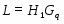


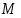
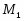

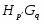
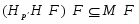
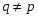
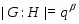
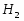

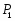
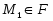
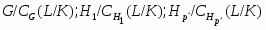
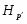
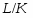
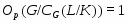
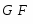

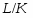
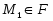
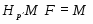
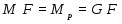

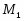

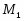
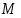
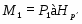

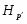
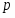
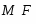
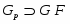


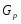
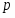

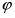
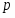
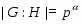

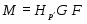

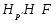
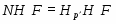
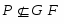
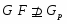
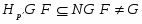
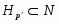
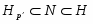
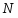



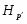
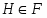


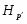
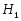
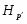
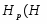

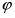
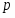
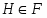
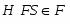
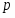

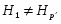


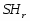

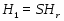
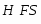

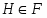
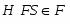


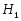

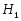

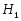
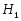

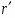
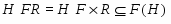
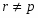
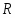
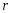


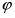
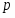
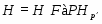
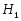
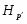

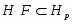


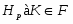


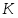
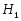
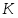
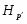
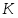
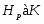


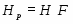
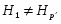

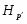
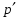
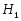

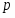
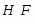


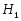
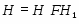









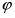



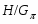
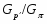
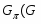
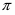
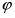
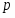

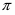
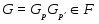

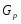
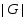
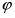
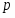






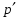




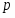
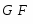



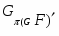

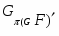




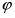



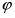






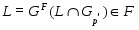


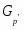
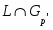
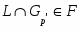


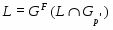


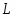

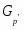



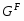
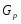




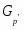



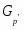
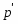
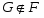





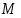
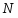

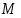
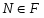


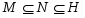
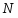



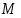
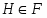
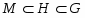

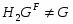
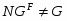


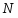
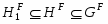
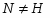
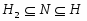
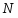


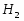

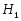

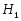








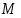
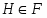
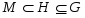



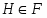







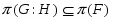
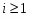
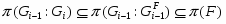
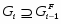
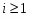
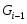


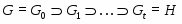
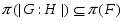



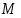

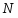
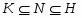
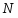



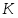
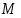
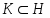

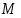
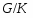

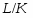
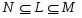
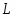


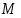
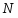
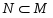
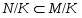
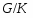

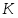
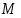
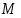


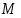

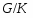
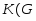






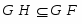
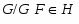
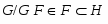
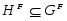

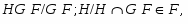








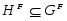






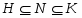
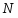



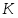








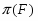


 Министерство образования Республики Беларусь
Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет
им. Ф. Скорины»
Математический факультет
Кафедра алгебры и геометрии
ОБЩИЕ СВОЙСТВА КОНЕЧНЫХ ГРУПП С УСЛОВИЕМ ПЛОТНОСТИ ДЛЯ -СУБНОРМАЛЬНЫХ ПОДГРУПП
Курсовая работа
Исполнитель:
Студентка группы М-33 ____________
Цыганцова А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент
____________ Скиба М.Т.
Гомель 2005
В работе все рассматриваемые группы предполагаются конечными. Используются обозначения, принятые в книгах. Буквами 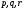 обозначаются простые числа.
обозначаются простые числа.
Будем различать знак включения множеств 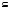 и знак строгого включения
и знак строгого включения 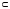 ;
;
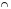 и
и 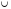 --- соответственно знаки пересечения и объединения множеств;
--- соответственно знаки пересечения и объединения множеств;
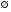 --- пустое множество;
--- пустое множество;
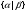 --- множество всех
--- множество всех 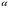 , для которых выполняется условие
, для которых выполняется условие 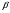 ;
;
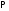 --- множество всех простых чисел;
--- множество всех простых чисел;
 --- некоторое множество простых чисел, т.е.
--- некоторое множество простых чисел, т.е. 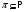 ;
;
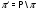 --- дополнение к
--- дополнение к  во множестве всех простых чисел; в частности,
во множестве всех простых чисел; в частности, 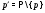 ;
;
примарное число --- любое число вида 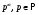 ;
;
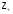 --- множество всех целых положительных чисел.
--- множество всех целых положительных чисел.
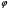 --- некоторое линейное упорядочение множества всех простых чисел
--- некоторое линейное упорядочение множества всех простых чисел 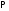 .
.
Запись 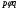 означает, что
означает, что 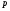 предшествует
предшествует 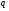 в упорядочении
в упорядочении 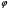 ,
, 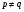 .
.
Пусть  --- группа. Тогда:
--- группа. Тогда:
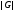 --- порядок группы
--- порядок группы  ;
;
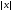 --- порядок элемента
--- порядок элемента  группы
группы  ;
;
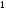 --- единичный элемент и единичная подгруппа группы
--- единичный элемент и единичная подгруппа группы  ;
;
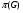 --- множество всех простых делителей порядка группы
--- множество всех простых делителей порядка группы  ;
;
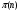 --- множество всех различных простых делителей натурального числа
--- множество всех различных простых делителей натурального числа  ;
;
 --группа --- группа
--группа --- группа  , для которой
, для которой 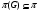 ;
;
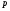 --группа --- группа
--группа --- группа  , для которой
, для которой 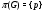 ;
;
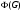 --- подгруппа Фраттини группы
--- подгруппа Фраттини группы  , т.е. пересечение всех максимальных подгрупп группы
, т.е. пересечение всех максимальных подгрупп группы  ;
;
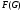 --- подгруппа Фиттинга группы
--- подгруппа Фиттинга группы  , т.е. произведение всех нормальных нильпотентных подгрупп группы
, т.е. произведение всех нормальных нильпотентных подгрупп группы  ;
;
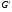 --- коммутант группы
--- коммутант группы  ;
;
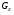 ---
---  --холловская подгруппа группы
--холловская подгруппа группы  ;
;
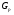 --- силовская
--- силовская 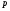 --подгруппа группы
--подгруппа группы  ;
;
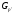 --- дополнение к силовской
--- дополнение к силовской 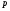 --подгруппе в группе
--подгруппе в группе  , т.е.
, т.е. 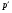 --холловская подгруппа группы
--холловская подгруппа группы  ;
;
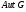 --- группа всех автоморфизмов группы
--- группа всех автоморфизмов группы  ;
;
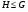 ---
--- 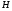 является подгруппой группы
является подгруппой группы  ;
;
нетривиальная подгруппа --- неединичная собственная подгруппа;
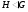 ---
--- 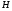 является нормальной подгруппой группы
является нормальной подгруппой группы  ;
;
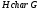 --- подгруппа
--- подгруппа 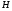 характеристична в группе
характеристична в группе  , т.е.
, т.е. 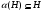 для любого автоморфизма
для любого автоморфизма 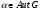 ;
;
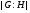 --- индекс подгруппы
--- индекс подгруппы 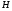 в группе
в группе  ;
;
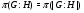 ;
;
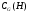 --- централизатор подгруппы
--- централизатор подгруппы 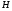 в группе
в группе  ;
;
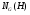 --- нормализатор подгруппы
--- нормализатор подгруппы 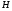 в группе
в группе  ;
;
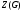 --- центр группы
--- центр группы  ;
;
 --- циклическая группа порядка
--- циклическая группа порядка  ;
;
Если 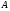 и
и 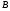 --- подгруппы группы
--- подгруппы группы  , то:
, то:
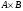 --- прямое произведение подгрупп
--- прямое произведение подгрупп 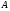 и
и 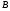 ;
;
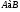 --- полупрямое произведение нормальной подгруппы
--- полупрямое произведение нормальной подгруппы 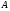 и подгруппы
и подгруппы 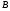 .
.
Группа  называется:
называется:
примарной, если 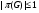 ;
;
бипримарной, если 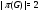 .
.
Скобки 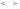 применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
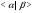 --- подгруппа, порожденная всеми
--- подгруппа, порожденная всеми 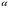 , для которых выполняется
, для которых выполняется 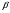 .
.
Группу  называют
называют 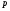 --нильпотентной, если
--нильпотентной, если 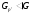 .
.
Группу  порядка
порядка 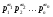 называют
называют 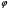 --дисперсивной, если выполняется
--дисперсивной, если выполняется 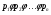 и для любого
и для любого 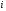
 имеет нормальную подгруппу порядка
имеет нормальную подгруппу порядка 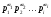 . Если при этом упорядочение
. Если при этом упорядочение 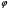 таково, что
таково, что 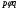 всегда влечет
всегда влечет 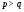 , то
, то 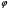 --дисперсивная группа называется дисперсивной по Оре.
--дисперсивная группа называется дисперсивной по Оре.
Цепь --- это совокупность вложенных друг в друга подгрупп. Ряд подгрупп --- это цепь, состоящая из конечного числа членов и проходящая через единицу. Цепь 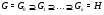 называется
называется 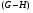 -цепью (с индексами
-цепью (с индексами 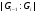 ); если при этом
); если при этом 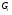 является максимальной подгруппой в
является максимальной подгруппой в 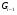 для любого
для любого 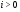 , то указанная цепь называется максимальной
, то указанная цепь называется максимальной 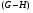 -цепью.
-цепью.
Ряд подгрупп 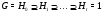 называется:
называется:
субнормальным, если 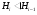 для любого
для любого 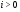 ;
;
нормальным, если 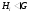 для любого
для любого 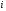 .
.
Нормальный ряд называется главным, если 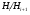 является минимальной нормальной подгруппой в
является минимальной нормальной подгруппой в 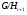 для всех
для всех 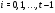 .
.
Классы групп, т.е. совокупности групп, замкнутые относительно изоморфизмов, обозначаются прописными готическими буквами. Так же обозначаются формации, т.е. классы групп, замкнутые относительно факторгрупп и подпрямых произведений. За некоторыми классами закреплены стандартные обозначения:
 --- класс всех групп;
--- класс всех групп;
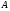 --- класс всех абелевых групп;
--- класс всех абелевых групп;
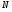 --- класс всех нильпотентных групп;
--- класс всех нильпотентных групп;
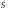 --- класс всех разрешимых групп;
--- класс всех разрешимых групп;
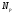 --- класс всех
--- класс всех 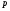 --групп;
--групп;
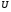 --- класс всех сверхразрешимых групп.
--- класс всех сверхразрешимых групп.
Пусть  --- некоторый класс групп и
--- некоторый класс групп и  --- группа, тогда:
--- группа, тогда:
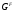 ---
---  --корадикал группы
--корадикал группы  , т.е. пересечение всех тех нормальных подгрупп
, т.е. пересечение всех тех нормальных подгрупп 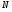 из
из  , для которых
, для которых 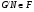 . Если
. Если  --- формация, то
--- формация, то 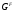 является наименьшей нормальной подгруппой группы
является наименьшей нормальной подгруппой группы  , факторгруппа по которой принадлежит
, факторгруппа по которой принадлежит  . Если
. Если 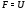 --- формация всех сверхразрешимых групп, то
--- формация всех сверхразрешимых групп, то 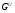 называется сверхразрешимым корадикалом группы
называется сверхразрешимым корадикалом группы  .
.
Формация  называется насыщенной, если всегда из
называется насыщенной, если всегда из 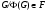 следует, что и
следует, что и 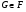 . Класс групп
. Класс групп 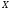 называется наследственным или
называется наследственным или 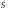 -замкнутым, если из того, что
-замкнутым, если из того, что 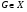 , следует, что и каждая подгруппа группы
, следует, что и каждая подгруппа группы  также принадлежит
также принадлежит 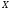 .
.
Пусть  --- некоторая непустая формация. Максимальная подгруппа
--- некоторая непустая формация. Максимальная подгруппа 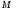 группы
группы  называется:
называется:
 -нормальной, если
-нормальной, если 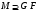 ;
;
 -абнормальной, если
-абнормальной, если 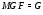 .
.
Максимальная 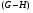 -цепь
-цепь  называется
называется  -субнормальной, если для любого
-субнормальной, если для любого 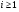 подгруппа
подгруппа 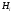
 -нормальна в
-нормальна в 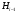 . Подгруппа
. Подгруппа 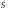 группы
группы  называется
называется  -субнормальной, если существует хотя бы одна
-субнормальной, если существует хотя бы одна  -субнормальная максимальная
-субнормальная максимальная 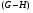 -цепь.
-цепь.
Группа  называется группой с плотной системой
называется группой с плотной системой  -субнормальных подгрупп, если для любых двух различных подгрупп
-субнормальных подгрупп, если для любых двух различных подгрупп 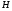 и
и 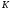 группы
группы  , из которых первая содержится во второй и не максимальна в ней, в группе
, из которых первая содержится во второй и не максимальна в ней, в группе  существует такая
существует такая  -субнормальная подгруппа
-субнормальная подгруппа 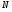 , что
, что 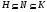 . В этом случае также говорят, что множество
. В этом случае также говорят, что множество  -субнормальных в
-субнормальных в  подгрупп плотно.
подгрупп плотно.
Изучение строения групп по заданным свойствам системы их подгрупп является одним из основных направлений в теории конечных групп. Отметим, что темп и глубина таких исследований непрерывно возрастают. Это направление изучения групп берет свое начало с групп Миллера-Морено, групп Шмидта. В качестве свойств, налагаемых на системы подгрупп, рассматривались абелевость, нормальность, субнормальность, дополняемость и др. Это направление получило широкое развитие в работах многих ведущих алгебраистов.
С дедекиндовых групп, то есть групп, у которых нормальны все подгруппы, началось изучение различных (как конечных, так и бесконечных) групп, у которых некоторая система подгрупп  удовлетворяет условию нормальности. Описание конечных дедекиндовых групп дано в работе Р. Дедекинда, а бесконечных в работе Р. Бэра. Эти работы определили важное направление исследований в теории групп. Главной целью этого направления является описание обобщенно дедекиндовых групп. Эти обобщения дедекиндовых групп осуществляются либо путем сужения системы подгрупп
удовлетворяет условию нормальности. Описание конечных дедекиндовых групп дано в работе Р. Дедекинда, а бесконечных в работе Р. Бэра. Эти работы определили важное направление исследований в теории групп. Главной целью этого направления является описание обобщенно дедекиндовых групп. Эти обобщения дедекиндовых групп осуществляются либо путем сужения системы подгрупп  , то есть подгрупп нормальных во всей группе, либо ослабления свойства нормальности для подгрупп из
, то есть подгрупп нормальных во всей группе, либо ослабления свойства нормальности для подгрупп из  . Среди таких обобщений выделим следующие исследования.
. Среди таких обобщений выделим следующие исследования.
Первое существенное обобщение дедекиндовых групп принадлежит О.Ю. Шмидту. Он описал конечные группы с одним и двумя классами сопряженных ненормальных подгрупп, а также установил нильпотентность конечной группы, у которой нормальны все максимальные подгруппы. Конечные группы с нормальными 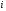 -тыми максимальными подгруппами изучали Б. Хупперт и З. Янко. Д.Бакли изучал конечные группы, у которых нормальны все минимальные подгруппы.
-тыми максимальными подгруппами изучали Б. Хупперт и З. Янко. Д.Бакли изучал конечные группы, у которых нормальны все минимальные подгруппы.
Значительные расширения класса дедекиндовых групп возникают при переходе от условия нормальности к различным ее обобщениям, как, например, к квазинормальности, субнормальности, нормализаторным условиям и др.
В начале 70-х годов по инициативе С.Н.Черникова началось изучение групп с плотными системами подгрупп. Система подгрупп группы  , обладающая некоторым свойством
, обладающая некоторым свойством  , называется плотной в
, называется плотной в  , если для любых двух подгрупп
, если для любых двух подгрупп 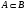 из
из  , где
, где 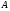 не максимальна в
не максимальна в 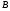 , найдется
, найдется  -подгруппа
-подгруппа 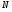 такая, что
такая, что  . Группы с плотной системой дополняемых подгрупп были изучены С.Н.Черниковым.
. Группы с плотной системой дополняемых подгрупп были изучены С.Н.Черниковым.
В 1974 году С.Н.Черников поставил следующий вопрос: каково строение группы  , в которой множество всех ее субнормальных подгрупп плотно? Ответ на этот вопрос был получен А.Манном и В.В.Пылаевым.
, в которой множество всех ее субнормальных подгрупп плотно? Ответ на этот вопрос был получен А.Манном и В.В.Пылаевым.
Заметим, что в теории формаций понятие субнормальности обобщается следующим образом. Говорят, что подгруппа 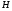 является
является  -субнормальной в
-субнормальной в  , если существует цепь подгрупп
, если существует цепь подгрупп
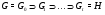
такая, что 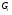 является
является  -нормальной максимальной подгруппой в
-нормальной максимальной подгруппой в 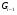 для любого
для любого 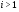 . Если
. Если  совпадает с классом всех нильпотентных групп (который является, конечно,
совпадает с классом всех нильпотентных групп (который является, конечно, 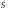 -замкнутой насыщенной формацией), то
-замкнутой насыщенной формацией), то  -субнормальная подгруппа оказывается субнормальной.
-субнормальная подгруппа оказывается субнормальной.
В связи с развитием теории формаций большое внимание стало уделяться исследованию конечных групп, насыщенных  --подгруппами,
--подгруппами,  --субнормальными или
--субнормальными или  --абнормальными подгруппами. В этом направлении проводили свои исследования Л.А.Шеметков, Гашюц, Картер, Шмид, Хоукс и другие.
--абнормальными подгруппами. В этом направлении проводили свои исследования Л.А.Шеметков, Гашюц, Картер, Шмид, Хоукс и другие.
Ясно, что вопрос С.Н.Черникова можно сформулировать в следующей общей форме: если  ---
--- 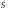 -замкнутая насыщенная формация, то каково строение группы, в которой множество всех ее
-замкнутая насыщенная формация, то каково строение группы, в которой множество всех ее  -субнормальных подгрупп плотно?
-субнормальных подгрупп плотно?
В таком виде вопрос С.Н.Черникова был исследован в работе для случая, когда  --- класс всех
--- класс всех 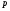 -нильпотентных групп. В настоящей работе мы исследуем данный вопрос в случаях, когда
-нильпотентных групп. В настоящей работе мы исследуем данный вопрос в случаях, когда  --- произвольная
--- произвольная 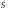 -замкнутая насыщенная формация либо
-замкнутая насыщенная формация либо 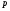 -нильпотентных, либо
-нильпотентных, либо 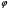 -дисперсивных, либо сверхразрешимых групп.
-дисперсивных, либо сверхразрешимых групп.
1. Определение и основные свойства конечных групп с условием плотности для -субнормальных подгрупп
Опишем вначале общие свойства конечных групп с плотной системой -субнормальных подгрупп, где --- произвольная насыщенная -замкнутая формация.
Группа называется группой с плотной системой -субнормальных подгрупп, если для любых двух различных подгрупп и группы , из которых первая содержится во второй и не максимальна в ней, в группе существует такая -субнормальная подгруппа , что . В этом случае также говорят, что множество -субнормальных в подгрупп плотно.
Пусть --- непустая -замкнутая насыщенная формация, --- подгруппа группы . Тогда справедливы следующие утверждения:
1) ;
2) если -субнормальна в и является подформацией формации , то -субнормальна в .
Доказательство. 1) Из того, что
следует, что . Это значит, что .
2) Так как , то и . Отсюда следует, что каждая -нормальная максимальная подгруппа является -нормальной максимальной. Лемма доказана.
Пусть --- непустая -замкнутая насыщенная формация. Если множество всех -субнормальных подгрупп плотно в группе , то справедливы следующие утверждения:
1) если , то в множество всех -субнормальных подгрупп плотно;
2) если --- подгруппа из , то множество всех -субнормальных подгрупп из является плотным в .
Доказательство. 1) Пусть --- нормальная подгруппа группы . В фактор-группе рассмотрим две произвольные подгруппы , из которых первая не максимальна во второй. Тогда и не максимальна в . По условию, в существует -субнормальная подгруппа такая, что . Следовательно, -субнормальна в .
2) Пусть --- подгруппа из и --- две произвольные подгруппы из такие, что не максимальна в . Тогда, по условию, в существует -субнормальная подгруппа , для которой . Ввиду леммы, -субнормальна в . Лемма доказана.
Если --- -субнормальная подгруппа группы , то
.
Доказательство. По определению, существует цепь
такая, что является -нормальной максимальной подгруппой в при любом . Таким образом, и потому
для каждого . Следовательно, .
Пусть --- непустая -замкнутая насыщенная формация, --- группа, у которой множество всех ее -субнормальных подгрупп плотно. Справедливы следующие утверждения:
1) если --- -абнормальная максимальная подгруппа группы , то либо , либо каждая -абнормальная максимальная подгруппа из принадлежит ;
2) если и , то либо максимальна в , либо -субнормальна в .
Доказательство. Докажем сначала 1). Пусть --- -абнормальная максимальная подгруппа, не принадлежащая . Допустим, что обладает -абнормальной максимальной подгруппой , не принадлежащей . Тогда в имеется -абнормальная максимальная подгруппа . По условию, в найдется такая -субнормальная подгруппа , что . Ясно, что . По лемме Error: Reference source not found,
.
Так как -субнормальна, то она содержится в -нормальной максимальной подгруппе, и поэтому . Значит, . Последнее противоречит следующему:
Докажем 2). Пусть и . Допустим, что не максимальна в . По условию, в найдется такая -субнормальная подгруппа , что . Так как -замкнута, то . Поэтому -субнормальна в . Теперь ясно, что -субнормальна в . Лемма доказана.
Пусть --- насыщенная -замкнутая формация, --- группа с нормальной силовской -подгруппой , удовлетворяющая следующим условиям:
1) ;
2) холлова -подгруппа -группы является максимальной в и принадлежит ;
3) любая собственная подгруппа из -субнормальна в .
Тогда является минимальной не -группой.
Доказательство. Из условия прямо следует, что совпадает с и является минимальной нормальной подгруппой в . Понятно, что каждая -абнормальная максимальная подгруппа из сопряжена с и поэтому принадлежит . Пусть --- произвольная -нормальная максимальная подгруппа из . Тогда . Так как -замкнута, то . Подгруппа является собственной в и по условию -субнормальна в . По теореме Error: Reference source not found,
.
Итак, каждая максимальная подгруппа из принадлежит . Лемма доказана.
2. Свойства максимальных подгрупп в группах с плотной системой -субнормальных подгрупп
В данном разделе изучаются свойства максимальных подгрупп конечных групп с плотной системой -субнормальных подгрупп, где --- произвольная насыщенная -замкнутая формация.
Пусть далее --- некоторое фиксированное упорядочение множества всех простых чисел.
Пусть --- произвольная насыщенная -замкнутая формация, --- -дисперсивная группа с плотной системой -субнормальных подгрупп, не принадлежащая , у которой все -абнормальные максимальные подгруппы принадлежат . Тогда справедливо одно из следующих утверждений:
1) --- максимальная подгруппа в ;
2) --- максимальна в -абнормальной максимальной подгруппе из .
Доказательство. Пусть --- группа минимального порядка, для которой лемма не верна. По теореме --- -группа. Пусть --- -абнормальная максимальная подгруппа группы . Тогда содержит некоторую -холлову подгруппу . По нашему предположению, не максимальна в . Тогда по лемме -субнормальна в . Если --- -максимальный простой делитель , то подгруппа нормальна в . Тогда, по теореме Error: Reference source not found,
.
Противоречие. Пусть --- множество простых делителей порядка группы , больших при упорядочении . По доказанному выше множество не пусто. Тогда . По индукции максимальна в . Противоречие. Лемма доказана.
Пусть --- произвольная насыщенная -замкнутая формация, --- -дисперсивная группа с плотной системой -субнормальных подгрупп, не принадлежащая . Тогда любая -абнормальная максимальная подгруппа из либо принадлежат , либо является минимальной не -группой, у которой нормальная силовская подгруппа является минимальной нормальной подгруппой.
Доказательство. Предположим, что утверждения леммы не выполняются и в существует -абнормальная максимальная подгруппа , не удовлетворяющая утверждениям леммы. Ввиду леммы и теоремы, , где --- -абнормальная максимальная подгруппа из , --- -группа, . Очевидно, что содержит некоторую -холлову подгруппу из .
1. Предположим, что . Если , то каждая -нормальная максимальная подгруппа группы будет иметь вид , где --- некоторая максимальная подгруппа из . Так как не максимальна в , то, по лемме Error: Reference source not found, -субнормальна в . Тогда по теореме Error: Reference source not found и --- минимальная не -группа. Предположим теперь, что . Если предположить, что , то не максимальна в . Тогда . Если не -максимальный простой делитель порядка группы , то в существует нормальная силовская -подгруппа , . Тогда подгруппа
.
Если -холлова подгруппа из не максимальна в , то применяя лемму и теорему, получаем, что . Пусть максимальна в . Тогда каждая собственная подгруппа из будет не максимальна в и, следовательно, по лемме, -субнормальна в . Если подгруппа , то, по теореме, . максимальна в , так как в противном случае не максимальна в . Применяя лемму и теорему, получаем, что --- минимальная не -группа и -корадикал группы является силовской -подгруппой. Так как по нашему предположению , то порядок группы делится на и, следовательно, . Тогда, по теореме Error: Reference source not found, . Противоречие. Значит, --- -максимальный простой делитель порядка группы . Тогда и каждая собственная подгруппа из не максимальна в . Если -субнормальна в , то по теореме . Так как не максимальна в , то, по условию, найдется -субнормальная в подгруппа такая, что
.
Так как , то
.
Отсюда следует, что и . Очевидно, что . Подгруппа содержится в некоторой -нормальной максимальной подгруппе из .
1.1
Тогда --- -максимальный простой делитель порядка группы и силовская -подгруппа группы нормальна в . Отсюда следует, что . Так как --- -группа, то содержится в некоторой -абнормальной максимальной подгруппе группы . По индукции либо принадлежит формации, либо является минимальной не -группой. Если --- минимальная не -группа, то и . Противоречие. Значит, . Пусть --- -главный фактор из . Но так как , то --- -главный фактор и выполняется изоморфизм . Так как , то --- -центральный -главный фактор. Противоречие.
1.2 ,
Так как , то содержится в некоторой -абнормальной максимальной подгруппе группы . Тогда в существует -абнормальная максимальная подгруппа . Если не максимальна в , то, по лемме, -субнормальна в . Противоречие. Значит, максимальна в . По условию найдется -субнормальная в подгруппа такая, что
.
Так как , то . Если , то и, следовательно, -субнормальна в . Значит, . Но тогда -субнормальна в . Противоречие.
2. и --- минимальная нормальная подгруппа в . Если каждая максимальная подгруппа из -субнормальна в , то --- минимальная не -группа. Значит, в найдется максимальная подгруппа , не -субнормальная в . Очевидно, что . Рассмотрим подгруппу . Подгруппа содержится в некоторой -абнормальной максимальной подгруппе из . Так как не максимальна в , то, по условию, в существует -субнормальная подгруппа такая, что . Так как и , то . Рассмотрим подгруппу . Подгруппа содержится в некоторой -абнормальной максимальной подгруппе из . По индукции либо принадлежит , либо является минимальной не -группой.
2.1
Тогда . Если предположить, что является -максимальным простым делителем порядка группы , , то силовская -подгруппа нормальна в и, по теореме,
.
Значит, --- -максимальный простой делитель порядка группы . Это значит, что и . Пусть --- минимальная не -группа. Тогда совпадает с силовской -подгруппой группы и, следовательно, . Получили, что . С другой стороны, -субнормальна в , а значит, и в . Поэтому
.
Противоречие. Значит, . Это значит, что . Из того, что максимальна в , а максимальна в , следует, что --- абелева дополняемая в подгруппа. Так как и , то и . По теореме Гашюца имеет дополнение в . Так как не максимальна в , то, по условию, найдется -субнормальная в подгруппа такая, что . Из того, что следует, что . Но тогда -субнормальна в . Противоречие.
2.2
Тогда --- силовская -подгруппа группы . Рассмотрим -холлову подгруппу группы , содержащую . Так как , то содержится в некоторой -абнормальной максимальной подгруппе группы . Если не максимальна в , то будет -субнормальна в . Потому максимальна в . Ввиду теоремы --- -группа. Если , то, согласно доказанному выше, лемма верна. Значит, --- минимальная нормальная подгруппа в . максимальна в . Подгруппа содержится в некоторой -абнормальной максимальной подгруппе группы . Так как не максимальна в , то, по условию, найдется -субнормальная в подгруппа такая, что . Так как , то . Но подгруппа будет содержаться в подгруппе группы . Если , то -субнормальна в . Если же , то получаем противоречие с тем, что --- -абнормальная максимальная подгруппа группы . Теорема доказана
3. Описание конечных не -групп с плотной системой -субнормальных подгрупп
В работе Закревской Л.Н. был исследован вопрос о строении группы , в которой множество всех ее -субнормальных подгрупп плотно для случая, когда --- класс всех -нильпотентных групп. При рассмотрении произвольной формации возможен случай, когда . Строение таких групп исследуется в в данном разделе.
Пусть --- произвольная насыщенная -замкнутая формация, --- группа с плотной системой -субнормальных подгрупп, не принадлежащая формации , . Тогда разрешима.
Доказательство. Пусть и --- группа минимального порядка, для которой теорема не верна. Так как , то содержит все силовские -подгруппы, . Следовательно, каждая -субнормальная подгруппа должна содержать все силовские -подгруппы, .
Пусть --- силовская -подгруппа группы и . Тогда если в ней существует вторая максимальная подгруппа, то, по условию, найдется -субнормальная подгруппа такая, что . Тогда, по доказанному, содержит все силовские -подгруппы, . Противоречие. Значит, в нет вторых максимальных подгрупп и .
Предположим, что . Тогда каждая максимальная подгруппа группы будет -абнормальной в . Пусть некоторая неединичная силовская подгруппа группы . Если предположить, что в существует вторая максимальная подгруппа, то, по условию, найдется -субнормальная в подгруппа такая, что . Отсюда следует, что . Противоречие. Следовательно, --- простое число. Получили, что каждая неединичная силовская подгруппа из имеет простой порядок и, значит, разрешима, что противоречит нашему предположению.
Пусть теперь . Так как, по доказанному, , то . Тогда по индукции --- разрешимая группа. По доказанному, каждая силовская подгруппа фактор-группы имеет простой порядок, и, значит, разрешима. Следовательно, разрешима и сама группа . Лемма доказана.
Пусть --- непустая -замкнутая насыщенная формация, --- группа, в которой множество всех -субнормальных подгрупп плотно, . Тогда --- группа одного из следующих типов:
1) , , ;
2) , , максимальна в , , ;
3) , , .
Доказательство. По лемме, разрешима. Так как , то ясно, что . Положим и рассмотрим холлову -подгруппу группы . Если единичная подгруппа не является максимальной в , то существует -субнормальная в подгруппа такая, что . По лемме Error: Reference source not found, и, значит, --- -группа. Получили противоречие. Таким образом, равен либо 1, либо является простым числом.
Рассмотрим теперь холлову -подгруппу группы . Пусть --- нормальная максимальная подгруппа из . Пусть , . Если 1 не максимальна в , то между 1 и можно вставить -субнормальную подгруппу, индекс которой, по лемме Error: Reference source not found, является -числом. Понятно, что этот индекс делится на . Получаем противоречие. Значит, равен либо квадрату простого числа, либо простому числу, либо произведению двух различных простых чисел.
Если , то ясно, что либо типа 1), либо типа 3). Пусть --- простое число. Если --- простое число, то --- группа типа 1). Пусть , где --- простые числа. Предположим, что в существует подгруппа порядка . Так как 1 не максимальна в , то между 1 и существует, по условию, -субнормальная подгруппа, индекс которой, по лемме, является -числом. Но этот индекс делится и на . Остается принять, --- максимальная подгруппа группы . Но тогда и --- группа типа 2). Теорема доказана.
Приведем пример, показывающий, что классы групп, перечисленные в теореме, не пусты.
Пусть --- такая -замкнутая насыщенная формация -нильпотентных групп, что не совпадает с множеством всех простых чисел. Пусть --- любое простое число, не входящее в . Тогда всякая группа порядка , где --- любое простое число, является группой типа 1), а всякая группа порядка или является группой типа 3) теоремы. Предположим, что и существует такое простое число , что и (в частности, можно взять и ). В сплетении группы порядка с группой порядка возьмем подгруппу Шмидта . Тогда имеет порядок и является группой типа 2) теоремы.
В данной работе рассматривались конечные группы с плотной системой -субнормальных подгрупп, где --- произвольная -замкнутая насыщенная формация. В первом разделе данной главы установлены общие свойства, которые могут быть использованы для изучения строения конечных групп с плотной системой -субнормальных подгрупп. Во втором разделе исследуются свойства максимальных подгрупп в конечных группах с плотной системой -субнормальных подгрупп. В частности, установленно, что в -дисперсивной группе с плотной системой -субнормальных подгрупп каждая -абнормальная максимальная подгруппа либо принадлежат , либо является минимальной не -группой, у которой нормальная силовская подгруппа является минимальной нормальной подгруппой. В третьем разделе данной главы описаны конечные группы с плотной системой -субнормальных подгрупп в случае, когда --- произвольная -замкнутая насыщенная формация и .
1.Гольфанд Ю.А. О группах, все подгруппы которых специальные // Докл. АН СССР. --- 1948. --- Т. 60,№ 8. --- C. 1313--1315.
2.Закревская Л.Н. Конечные группы с плотной системой  -субнормальных подгрупп // в кн: Исследование нормального и подгруппового строения конечных групп. --- Минск:Наука и техника, 1984. --- 71--88.
-субнормальных подгрупп // в кн: Исследование нормального и подгруппового строения конечных групп. --- Минск:Наука и техника, 1984. --- 71--88.
3.Закревская Л.Н. Конечные группы с -плотной системой подгрупп // в кн: Арифметическое и подгрупповое строение конечных групп. --- Мн.:Наука и техника, 1986. --- 59--69.
4.Каморников С.Ф., Селькин М.В. Подгрупповые функторы и классы конечных групп. --- Минск:Бел. навука, 2003. --- 254 с.
5.Кехмадзе Ш.С. Квазинильпотентные группы // Докл. АН СССР. --- 1964. --- № 155. --- С. 1003--1005.
6.Монахов В.С. О влиянии свойств максимальных подгрупп на строение конечной группы // Матем. зам. --- 1972. --- Т. 11, № 2. --- C. 183--190.
7.Пылаев В.В. Конечные группы с плотной системой субнормальных подгрупп // в кн: Некоторые вопросы теории групп. --- Киев:Инст. математики АН УССР, 1975. --- С. 197--217.
8.Пылаев В.В. Конечные группы с обобщенно плотной системой субнормальных подгрупп // в кн: Исследования по теории групп. --- Киев:Инст. математики АН УССР, 1976. --- С. 111--138.
9.Семенчук В.Н. Минимальные не -группы // Алгебра и логика. --- 1979. --- Т. 18, № 3. --- C. 348--382.
10.Черников С.Н. Группы с плотной системой дополняемых подгрупп // Некоторые вопросы теории групп. --- Киев: Ин-т математики АН УССР, 1975. --- С. 5--29.
11.Черников С.Н. Группы с заданными свойствами системы бесконечных подгрупп // Укр. мат. журн. --- 1967. --- № 6. --- С. 111--131.
12.Черников С.Н. О нормализаторном условии // Мат. заметки. --- 1968. --- № 1. --- С. 45--50.
13.Чунихин С.А. О -свойствах конечных групп // Матем. сб. --- 1949. --- Т. 25, № 3. --- с. 321--346.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ