Оценка времени жизни кольца Плутона в атмосфере планеты
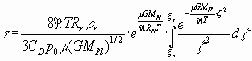
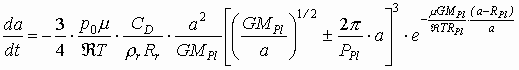
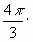
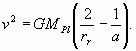
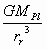
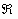
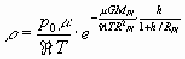
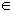
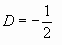 Оценка времени жизни кольца Плутона в атмосфере планеты
Оценка времени жизни кольца Плутона в атмосфере планеты
Н.И. Перов
Введение
На основании 60-летних наблюдений астрономов Главной астрономической обсерватории РАН периодических изменений блеска системы Плутон-Харон, происходящих с периодом 7,8 лет [3], в работе [2] , с использованием модели движения частицы в рамках дважды осреднённой ограниченной задачи трёх тел, с учётом сжатия Плутона, было сделано предположение о существовании вблизи Плутона на расстоянии 2510-2520 км гипотетического кольца, состоящего из частиц с характерным радиусом Rr. Поскольку радиус Плутона составляет RPl =1137 км [4], то естественно ожидать, что атмосфера Плутона будет ограничивать космогонический срок жизни такого кольца. Для состава атмосферы Плутона и величины давления на его поверхности получены приближённые оценки. В частности, в работе [4] утверждается, что атмосфера Плутона состоит в основном из азота, окиси углерода и примеси метана, а давление (p0) на поверхности планеты составляет всего несколько микробар при температуре (T) 35-45 K.
Поставим задачу определения космогонического времени жизни (τ) спутникоподобного объекта радиуса Rr, плотности ρr, который в начальный момент времени находится на круговой орбите на расстоянии rr от центра Плутона и движется в атмосфере планеты. Примем, что плотность атмосферы Плутона (ρ), при неизменной температуре, изменяется по экспоненциальному закону, при изменении ускорения свободного падения (g) с высотой. Вследствие торможения радиус орбиты объекта будет уменьшаться, и по истечении времени (τ) этот объект упадёт на поверхность Плутона (поверхность Плутона на 70% состоит из скальных пород и на 30% - из льда).
Основные уравнения
Известно [1], что объект, движущийся со скоростью V относительно окружающей его атмосферы, подвержен воздействию аэродинамических сил, которые можно разложить на две компоненты: сопротивление D, действующее в направлении, противоположном V, и силу в плоскости, перпендикулярной V. Выражение для D записывают в аэродинамике [1] обычно в виде
ρVVSCD , (1)
где
ρ - плотность окружающей среды,
S - характерная площадь объекта (обычно - это площадь сечения объекта плоскостью, перпендикулярной направлению движения).
В дальнейшем будем предполагать отсутствие сил в направлении, перпендикулярном движению (если бы они действовали, возникла бы компонента по направлению движения, изменяющая D и делающая изложенную ниже теорию несостоятельной).
Значение CD примем равным 2,2 в соответствии с монографией [1] , где показано, что для искусственных спутников Земли самой разнообразной формы и находящихся на различных высотах над поверхностью Земли CD (2,1 ; 2,35).
Плотность атмосферы Плутона зависит от многих факторов (расстояния Плутона от Солнца, солнечной активности, температуры дневного и ночного полушарий Плутона). Учитывая изменение ускорения свободного падения (g) с высотой (h), плотность (ρ) изотермической атмосферы Плутона представим в виде
, (2)
где μ - молярная масса (азота), RPl - радиус Плутона, - универсальная газовая постоянная, G - гравитационная постоянная, MPl - масса Плутона.
Величина V в формуле (1) в общем случае является скоростью движения объекта относительно окружающей среды (атмосферы Плутона). Если обозначить через v скорость движения объекта относительно центра масс Плутона, а через VA - скорость движения атмосферы планеты (вследствие осевого вращения Плутона с периодом PPl), то
V=v-VA (3)
С учётом возмущений от сопротивления атмосферы Плутона дифференциальное уравнение, описывающее орбитальную эволюцию частицы массы mr гипотетического кольца планеты, примет следующий вид
d2r/dt2 = - rr + D/mr (4)
В уравнении (4) второе слагаемое - ускорение, обусловленное торможением в среде - должно быть существенно меньше первого члена - гравитационного ускорения. При малых значениях величины |D/mr| скорость |v| приближённо будет совпадать со скоростью движения объекта по невозмущённой орбите
(5)
Здесь a - большая полуось орбиты частицы-спутника Плутона.
Рассматривая круговые (rr=a), экваториальные орбиты объектов (лежащие в плоскости экватора Плутона), выражая h через a и RPl,
h=a-RPl, (6)
Выражая S и mr через Rr и ρr (для сферических частиц) ,
S =πRr2; mr=Rr3ρr, (7)
От уравнений (1) - (7) (дифференцируя (5) по времени (t) и используя (4)) , перейдём к уравнению изменения большой полуоси орбиты (a) с течением времени (t) - da/dt
(8)
В уравнении (8) знак "-" соответствует одинаковым направлениям скоростей объекта и атмосферы Плутона, а знак "+" - противоположным . Для больших полуосей орбит мелких спутников Плутона, удовлетворяющих условию a<2520 км, в уравнении (8) можно пренебречь вторым членом в квадратных скобках по сравнению с первым с погрешностью в несколько процентов (при a=2520 км первое слагаемое равно 580 м/с, а второе, приближённо ~ 30 м/с). Замечая, что вблизи поверхности Плутона ускорение, возникающее вследствие торможения, может значительно превосходить гравитационное ускорение, а скорость объекта может заметно отличаться от скорости в невозмущённом движении (5) и формула (8) уже будет не применима, ограничимся интервалом больших полуосей орбит от aн =2520 км до aк=1337 км (полагаем, что рассматриваемые объекты прекращают своё существование на высоте 200 км от поверхности Плутона). Конечно, крупные (Rr>10 м) и плотные (ρr>1000 кг/м3 ) тела выпадают на поверхность планеты.
Разделяя в уравнении (8) переменные a и t, используя новую переменную ξ=1/ и интегрируя в пределах от ξн=6,299·10-4 м-1/2 до ξк=8,648·10-4 м-1/2, получим окончательную формулу для определения времени жизни τ объектов, образующих кольцо Плутона
(9)
Таким образом, при сделанных предположениях, время жизни спутникоподобных тел вблизи Плутона прямо пропорционально произведению радиусов этих тел и их плотности и обратно пропорционально давлению у поверхности планеты. Это время жизни также зависит сложным образом от других параметров, как атмосферы (μ, T), так и планеты (MPl, RPl).
ПРИМЕРЫ:
Для численных оценок определим время жизни: 1) "короткоживущих" и 2) "долгоживущих" частиц в атмосфере Плутона. Примем следующие значения параметров Плутона и его атмосферы [4]:
G=6,672·10-11 Нм2/кг2,
μ=28·10-3 кг/моль,
RPl=1137000 м,
MPl=1,27·1022 кг,
=8,31 Дж/(К·моль),
aн=2520000 м, ξн=6,299·10-4 м-1/2,
aк=1337000 м, ξк=8,648·10-4 м-1/2,
СВ=2,2.
Результаты вычислений для различных частиц и условий приведены в таблице (I - значение интеграла (9), вычисленного по методу Симпсона при 2m=200)
N
T
К
p0
Па
ρr
кг/м3
Rr
м
I
м1/2
Τ
годы
1
45
1
100
0,1
3,47·10-10
3,31·105
2
35
0,1
1000
1
2,05·10-13
1,28·1012
Из вышеизложенного следует, что время жизни крупных (Rr>10 м) и плотных (ρr>1000 кг/м 3) частиц в атмосфере Плутона превосходит на несколько порядков время жизни (τ) мелких (Rr<0,1 м) и рыхлых частиц (ρ<100 кг/м3). Это значит, что при большом возрасте (порядка 1 млрд. лет) гипотетического кольца Плутона оно должно состоять из сравнительно крупных объектов, а если это образование относительно молодое (105 лет), то не исключается наличие в нём, наряду с крупными, и мелких объектов.
Этот вывод можно будет проверить уже в первом десятилетии XXI века, если состоится первый полёт в систему Плутон-Харон (2008 г.) [http://www.seds.org/billa/tnp/Pluto.html].
Список литературы
Кинг-Хили Д. Теория орбит искусственных спутников в атмосфере. М.: Мир, 1966. 190 с.
Perov N.I. A method of localization of unknown minor bodies in multiple systems of major bodies / Proceedings of International Conference "AstroKazan-2001", September 24-29, 2001, Kazan State University: Publisher "DAC", 2001. P.253-256.
Rylkov V.P., Vityazev V.V., Dementieva A.A. Pluto: an analyses of photographic positions obtained with the Pulkovo normal astrograph in 1930-1992 / Astronomical Transactions. 1995. V. 6. P. 265-281.
Tholen D. Pluto and Charon. The University of Arizona. Tucson. Arizona. 1997.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ