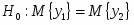
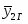
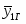
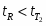
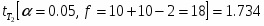
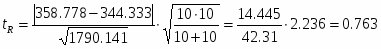
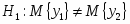
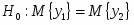
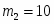
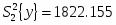
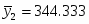
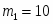
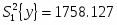
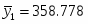
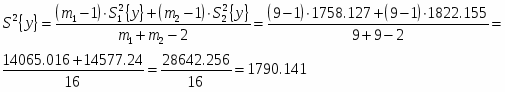
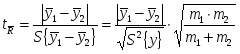
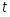
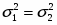
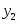
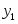
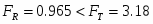
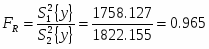
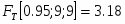
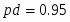
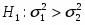
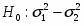
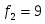
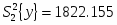
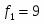
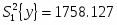
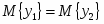
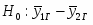
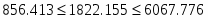
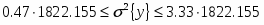
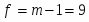
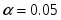
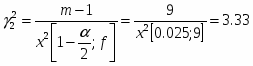
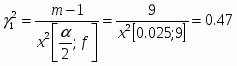
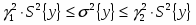
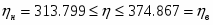
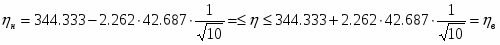
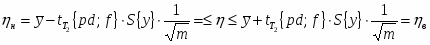
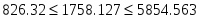
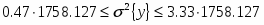
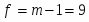
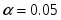
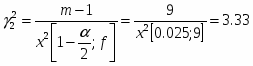
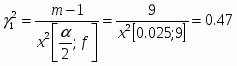
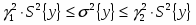
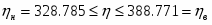
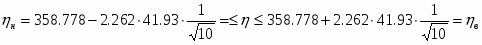
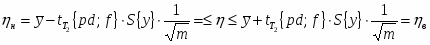
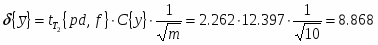
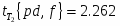
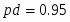
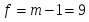
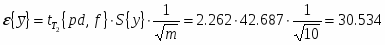
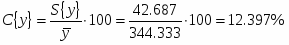
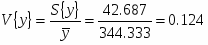
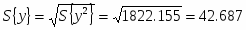
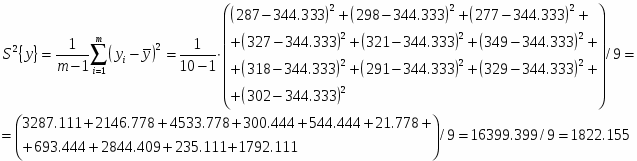
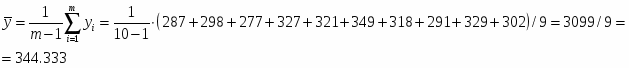
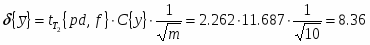
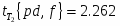
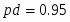
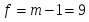
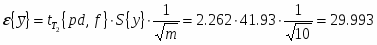
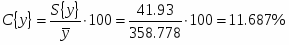
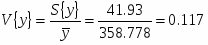
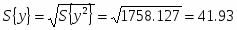
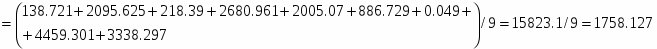
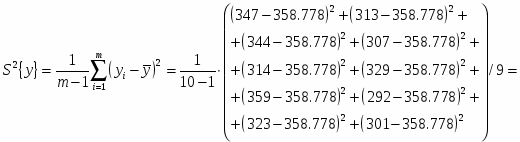
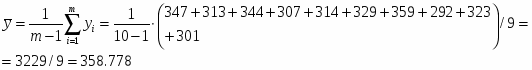
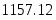
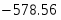
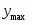
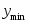
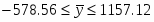
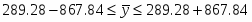
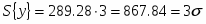
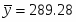
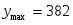
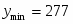
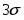
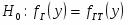
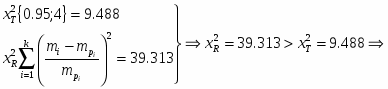
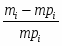
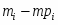
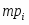
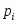
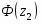
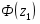
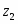
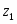
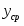
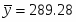
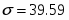
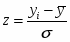
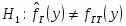
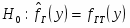
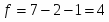
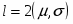
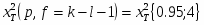
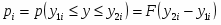
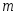
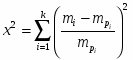
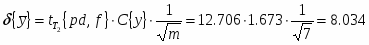
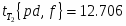
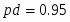
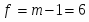
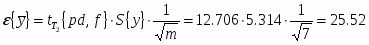
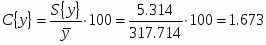
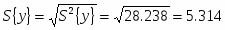
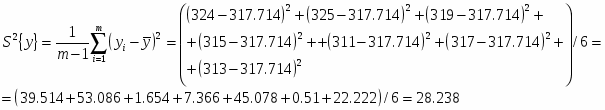
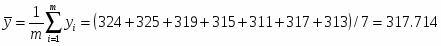
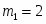
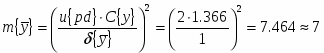
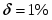
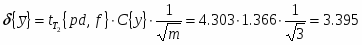
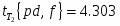
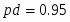
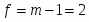
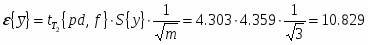
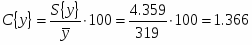
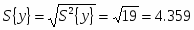
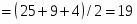
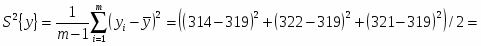
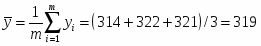
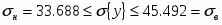
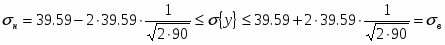
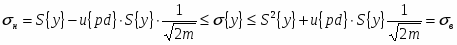
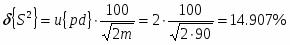
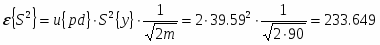
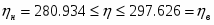
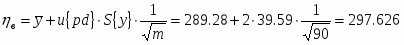
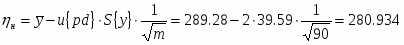
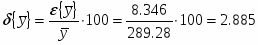
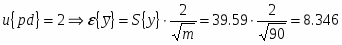
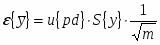
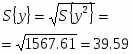
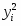
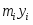
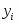
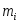
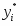
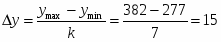
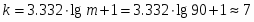
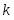
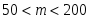1. Обработка одноуровневого технологического эксперимента (выборка В₁).

1. Построить эмпирический закон распределения для данной выборки.

342

321

324

325

365

347

287

317

313

318

330

330

277

310

331

313

298

325

296

327

337

318

329

345

324

344

277

359

355

299

283

289

328

356

319

307

327

337

346

290

332

322

366

282

344

314

321

310

304

301

317

316

339

363

323

329

349

382

294

320

308

313

300

335

311

359

318

296

320

319

280

317

314

376

321

292

291

333

300

319

302

322

346

323

315

323

329

333

328

304

265

325

320

349

353

301

302

277

292

300

при устанавливаем число :

величина интервала:

граница классов

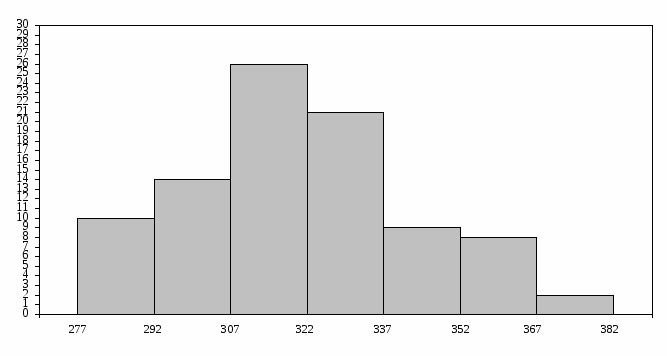
277-292

284.5

10

-2

-20

4

40

292-307

299.5

14

-1

-14

1

14

307-322

314.5

26

0

0

0

0

322-337

329.5

21

1

21

1

21

337-352

344.5

9

2

18

4

36

352-367

359.5

8

3

24

9

72

367-382

374.5

2

4

8

16

32

—

90

—

37

—

215

среднеквадратическое отклонение:

Эмпирический закон распределения выборки В₁

Гистограмма:

1. Определить точечные оценки (среднее, дисперсия).

Среднее значение:

Дисперсия:

1. Определить относительные ошибки и доверительные интервалы для генерального среднего и генеральной дисперсии.

Абсолютная доверительная ошибка среднего:

при ,

Относительная доверительная ошибка среднего:

Границы доверительного интервала среднего значения:

Абсолютная доверительная ошибка дисперсии:

– относительная доверительная ошибка

дисперсии

Граница доверительного интервала дисперсии:

1. Спланировать объём выборки, если при определении среднего относительная ошибка не должна превышать 1%.

Для планирования объёма выборки из В₁ выбираем 3 значения: 314, 322, 321.

Выборка В^*.

Числовые характеристики В^*:

– среднее значение

Дисперсия:

Среднее квадратичное отклонение:

Квадратичная неровнота:

Абсолютная доверительная ошибка:

где ;

Относительная доверительная ошибка:

Доверительный объём измерений:

Реализуем выборку объёма . Для этого выбираем 2 значения: 324, 325, 319, 315, 311, 317, 313.

Выборка В^**.

Числовые характеристики В^**:

– среднее значение

Дисперсия:

Среднее квадратичное отклонение:

Квадратичная неровнота:

Абсолютная доверительная ошибка:

где ;

Относительная доверительная ошибка:

1. Проверить гипотезу о пропорциональности технологического параметра для заданной выборки.

Проверка гипотезы осуществляется по критерию х²:

где – объём выборки; – частота попадания в i – классе; k – число классов; – вероятность попадания в i – интервал.

где ; – число степени свободы

Рассмотрим гипотезу , при конкурирующей

Введём новое значение , где ;

i

интервал

1

277-292

284.5

0.31

0.07

0.1217

0.0279

0.0938

8.442

1.558

0.184

2

292-307

299.5

0.07

0.45

0.0279

0.1736

0.1457

13.113

0.887

0.068

3

307-322

314.5

0.45

0.83

0.1736

0.2967

0.1231

11.079

14.921

1.347

4

322-337

329.5

0.83

1.205

0.2967

0.3944

0.0977

8.793

12.207

1.388

5

337-352

344.5

1.205

1.58

0.3944

0.4429

0.0485

4.365

4.635

1.062

6

352-367

359.5

1.58

1.96

0.4429

0.4750

0.0321

2.889

5.111

1.769

7

367-382

374.5

1.96

2.34

0.4750

0.4903

0.0153

1.377

0.623

0.452

6.27

гипотеза о нормальности технологического процесса не принимается.

1. Проверить наличие резко выделяющихся значений в выборке (метод ).

и находятся в пределах интервала (; ), следовательно резко выделяющихся значений в выборке нет.

1. Обработка сравнительного технологического эксперимента.

Подготовка данных: сформировать из исходного массива В₁ методом рандомизации две выборки малого объёма В₂ и В₃ для дальнейших исследований.

1. Определить числовые характеристики выборок В₂ и В₃.

В₂

В₃

1

347

287

2

313

298

3

344

277

4

307

327

5

314

321

6

329

349

7

359

318

8

292

291

9

323

329

10

301

302

Числовые характеристики выборки В₂.

Среднее значение:

Дисперсия:

Среднее квадратичное отклонение:

Коэффициент вариации:

Квадратичная неровнота:

Абсолютная доверительная ошибка среднего значения:

где ;

Относительная доверительная ошибка среднего значения:

Числовые характеристики выборки В₃.

Среднее значение:

Дисперсия:

Среднее квадратичное отклонение:

Коэффициент вариации:

Квадратичная неровнота:

Абсолютная доверительная ошибка среднего значения:

где ;

Относительная доверительная ошибка среднего значения:

1. Определить доверительные интервалы для генерального среднего и генеральной дисперсии.

Доверительный интервал для среднего значения выборки В₂:

Доверительный интервал для дисперсии:

;

где ;

Доверительный интервал для среднего значения выборки В₃:

Доверительный интервал для дисперсии:

;

где ;

1. Проверка гипотезы о равенстве генеральных средних выборок В₂ и В₃: ; .

Сравниваем две дисперсии нормальных генеральных совокупностей с числом степеней свободы:

;

;

Оцениваем возможность принятия гипотезы .

При альтернативной гипотезе и доверительной вероятности находим:

т.к. , то выдвинутую гипотезу об однородности дисперсии или равной точности двух рядов измерений и надо принять.

Сравниваем две средние из нормальных распределений генеральных совокупностей.

Если доказана, то используется критерий :

,

где

;

;

Проверим гипотезу о равенстве средних:

при конкурирующей гипотезе

Затем находим расчётное значение критерия Стьюдента:

и его табельное значение

Т.к. , то генеральные средние и статически не различаются. Гипотеза принимается.