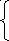
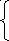
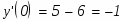
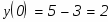
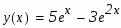
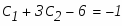
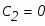
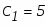
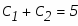
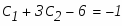
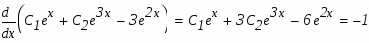
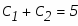
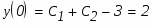
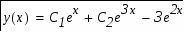
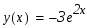
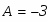
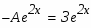
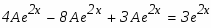
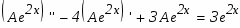
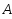
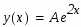
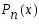
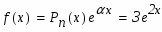
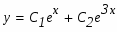
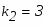
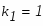
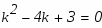
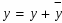
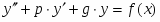
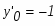
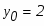
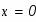
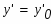
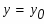
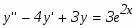
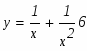
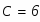
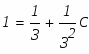
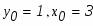
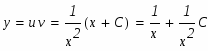
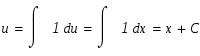
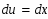
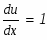
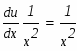
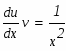
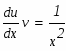
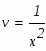
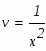
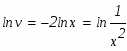
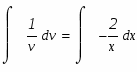
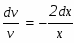
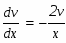
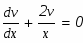
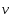
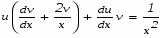
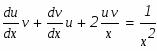
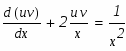
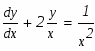
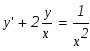
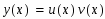
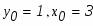
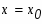
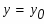
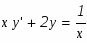
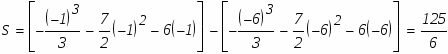
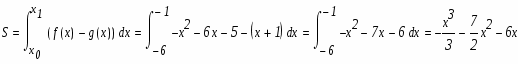
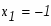
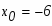
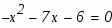
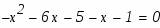
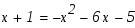
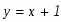
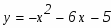
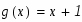
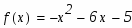
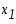
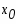
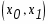
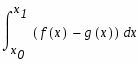
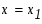
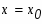
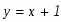
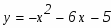
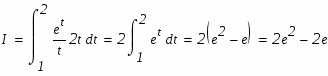
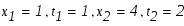
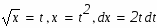
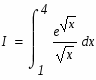
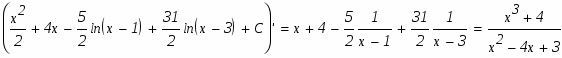
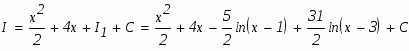
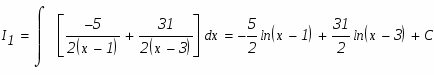
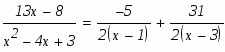
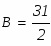
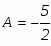
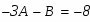
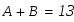
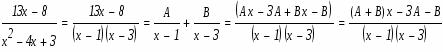
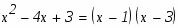
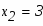
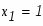
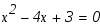
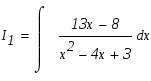
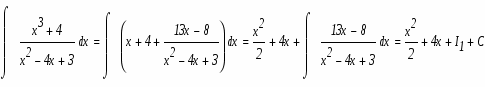
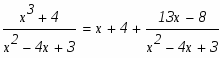
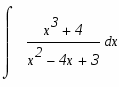
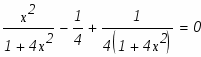
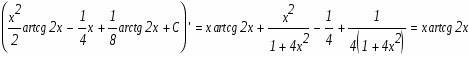
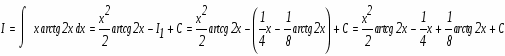
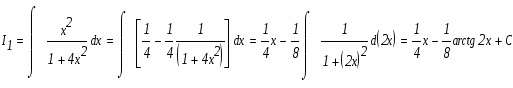
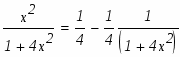
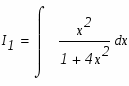
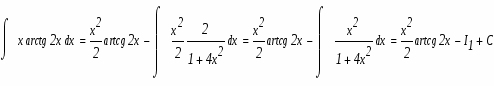
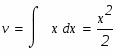
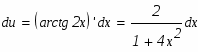
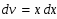
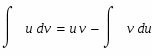
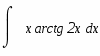
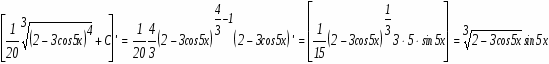
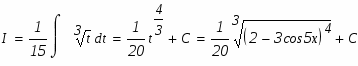
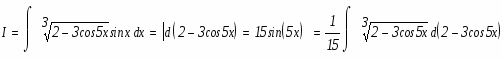
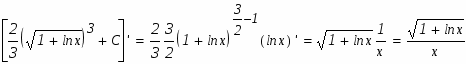
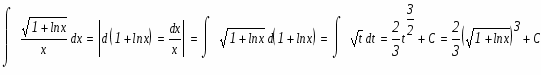Задание. Найти неопределенные интегралы. Результат проверить дифференцированием.

а)

Используемый прием интегрирования называется подведением под знак дифференциала. Проверим результат дифференцированием.

б)

В этом интеграле также используется подведение под знак дифференциала

Проверим результат дифференцированием.

в)

Для решения этого интеграла воспользуемся формулой интегрирования "по частям". Приведем формулу интегрирования по частям:

В этом интеграле распишем составляющие следующим образом:

Продифференцируем u и проинтегрируем dv чтобы мы могли применить формулу интегрирования по частям:

Подинтегральное выражение есть неправильная рациональная дробь. Необходимо привести ее к сумме правильных рациональных дробей, выполнив деление углом числитель на знаменатель.

Вернемся к исходному интегралу:

Проверим результат дифференцированием:

г)

интеграл дифференцирование уравнение парабола

Подинтегральное выражение является неправильной рациональной дробью. Необходимо преобразовать ее в сумму правильных рациональных дробей, выполнив деление углом числитель на знаменатель:

Подинтегральное выражение представляет собой правильную рациональную дробь. Чтобы проинтегрировать её необходимо её представить в виде суммы простейших дробей. Найдем корни знаменателя

по теореме Виета

Разложим правильную рациональную дробь в сумму простейших методом неопределенных коэффициентов:

Приравнивая коэффициенты при одинаковых степенях х, составим систему линейных алгебраических уравнений для определения неизвестных коэффициентов А и В:

Решая СЛАУ находим значения коэффициентов:

Возвратимся к исходному интегралу:

Результат проверим дифференцированием:

Задание. Вычислить по формуле Ньютона-Лейбница определенный интеграл.

Перейдем к замене переменных в определенном интеграле:

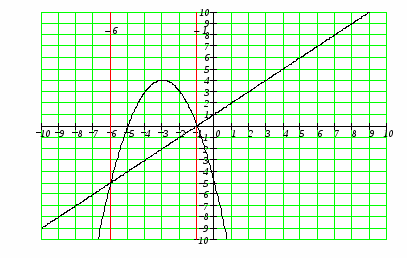
Задание. Вычислить площадь фигуры, ограниченной параболой и прямой . Сделать чертеж.

Решение. Площадь области S, ограниченной снизу функцией g(x), сверху- функцией f(x), слева - вертикальной прямой , справа - вертикальной прямой равна равна определенному интегралу:

Так как мы пока не знаем, какая же из функций является большей на отрезке , построим чертеж. Точки , являются абсциссами точек пересечения графиков этих двух функций.

Как видно из построения парабола лежит выше прямой на отрезке, поэтому:

Абсциссы точек пересечения суть соответственно -6 и -1. Эти значения мы также можем получить решив в системе уравнения двух кривых

по теореме Виета имеем: , . Теперь осталось только применить формулу вычисления площади криволинейной области:

-6

-1

Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию при

Решение: имеем линейное уравнение первого порядка. будем искать решение уравнения в виде произведения двух функций от х:

Запишем исходное выражение в виде:

Выберем функцию такой чтобы выражение в скобках равнялось нулю:

Разделяя переменные в этом дифференциальном уравнении относительно функции v, находим:

Так как выражение в скобках подобрано так, чтобы оно равнялось нулю, подставим найденное значение в уравнение для определения u.

Таким образом находим общее решение системы

Подберем переменную С так чтобы выполнились начальные условия , что будет являться частным решением дифференциального уравнения:

Полученное частное решение дифференциального уравнения, соответствующее поставленным начальным условиям.

Задание. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальным условиям , при . (,)

Решение: Пусть имеем неоднородное линейное уравнение второго порядка:

Структура общего решения такого уравнения определяется следующей теоремой:

Теорема: Общее решение неоднородного уравнения представляется как сумма какого-нибудь частного решения этого уравнения y* и общего уравнения y соответствующего однородного уравнения:

Чтобы найти общее решение соответствующего однородного уравнения (то есть такого, в котором правая часть равна нулю) необходимо найти корни характеристического уравнения и по ним определить вид решения.

Характеристическое уравнение в нашем случае есть:

имеет действительные и различные корни: , .

Общий интеграл есть:

Правая часть линейного уравнения второго порядка имеет вид: , где - многочлен 0-й степени, =2 (не является корнем характеристического многочлена).

поэтому частное решение следует искать в виде:

где - постоянный коэффициент, подлежащий определению. Подставляя y* в заданное уравнение, будем иметь:

Имеем решение . Итак, частное решение нашли в виде:

Таким образом, общий интеграл данного уравнения имеет вид:

Для определения коэффициентов С1 и С2 используем начальные условия:

При х=0 функция равна 2

При х=0 первая производная функции равна -1:

Составим систему из этих двух уравнений и решим её относительно неизвестных С1 и С2

Таким образом, частное решение данного дифференциального уравнения запишется в виде: