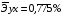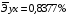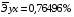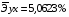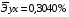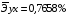Парная регрессия
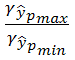
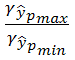
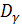
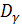
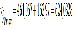
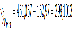
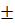
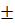
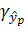
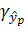

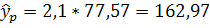
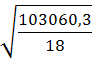
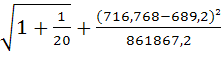
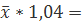
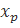
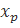
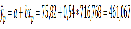
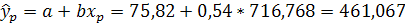
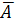
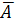


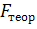
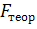


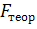
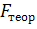





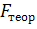
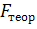
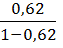




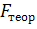
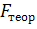
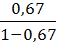




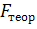
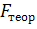
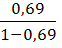




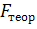
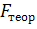
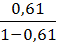




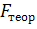
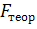
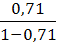


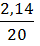
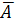
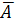
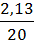
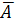
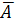
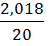
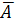
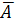
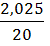
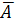
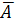
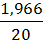
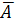
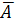
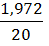
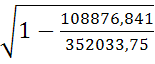
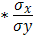
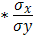

Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х1, Х2, … Хр и Y. При этом речь идет о влиянии переменных Х (это будут аргументы функций) на значения переменной Y (значение функции). Переменные Х мы будем называть факторами, а Y – откликом.
Наиболее простой случай – установление зависимости одного отклика y от одного фактора х. Такой случай называется парной (простой) регрессией.
Парная регрессия – уравнение связи двух переменных у и x:
 ,
,
где у – зависимая переменная (результативный признак);
х – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия: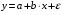 .
.
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
• полиномы разных степеней 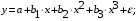
•равносторонняя гипербола 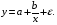
Регрессии, нелинейные по оцениваемым параметрам:
степенная
 ;
;показательная
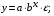
экспоненциальная
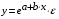
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических 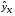 минимальна, т.е.
минимальна, т.е.
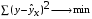
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно а и b:
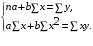
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
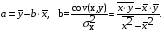
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции 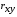 для линейной регрессии
для линейной регрессии 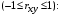
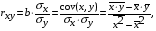
и индекс корреляции 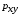 - для нелинейной регрессии (
- для нелинейной регрессии (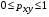 ):
):
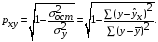
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
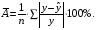
Допустимый предел значений 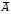 – не более 8 – 10%.
– не более 8 – 10%.
Средний коэффициент эластичности 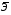 показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения:
показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения:
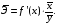
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
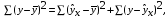
где 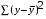 – общая сумма квадратов отклонений;
– общая сумма квадратов отклонений;
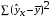 – сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
– сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
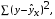 – остаточная сумма квадратов отклонений.
– остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R2:
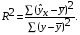
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
F-тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера. Fфакт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
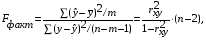
п – число единиц совокупности;
т – число параметров при переменных х.
Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.
Если Fтабл < Fфакт, то H0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если Fтабл > Fфакт, то гипотеза Н0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
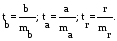
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
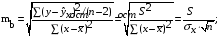
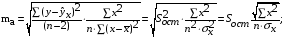
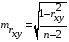
Сравнивая фактическое и критическое (табличное) значения t-статистики – tтабл и tфакт – принимаем или отвергаем гипотезу Hо.
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством
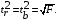
Если tтабл < tфакт, то Hо отклоняется, т.е. а, b и 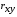 не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если tтабл > tфакт, то гипотеза Но не отклоняется и признается случайная природа формирования a, b или
не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если tтабл > tфакт, то гипотеза Но не отклоняется и признается случайная природа формирования a, b или 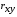 .
.
Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:
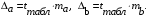
Формулы для расчета доверительных интервалов имеют следующий вид:

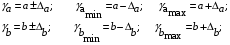
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение 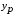 определяется путем подстановки в уравнение регрессии
определяется путем подстановки в уравнение регрессии 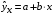 соответствующего (прогнозного) значения
соответствующего (прогнозного) значения 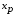 . Вычисляется средняя стандартная ошибка прогноза
. Вычисляется средняя стандартная ошибка прогноза 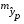 :
:
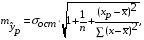 где
где 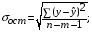
и строится доверительный интервал прогноза:
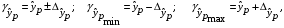 где
где 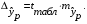
Задача:
По 22 регионам страны изучается зависимость розничной продажи телевизоров, y от среднедушевых денежных доходов в месяц, x (табл. 1):
№ региона
X
Y
1,000
2,800
28,000
2,000
2,400
21,300
3,000
2,100
21,000
4,000
2,600
23,300
5,000
1,700
15,800
6,000
2,500
21,900
7,000
2,400
20,000
8,000
2,600
22,000
9,000
2,800
23,900
10,000
2,600
26,000
11,000
2,600
24,600
12,000
2,500
21,000
13,000
2,900
27,000
14,000
2,600
21,000
15,000
2,200
24,000
16,000
2,600
34,000
17,000
3,300
31,900
19,000
3,900
33,000
20,000
4,600
35,400
21,000
3,700
34,000
22,000
3,400
31,000
Задание
Постройте поле корреляции и сформулируйте гипотезу о форме связи.
Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
Оцените тесноту связи с помощью показателей корреляции и детерминации.
С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
Качество уравнений оцените с помощью средней ошибки аппроксимации.
С помощью F-критерия Фишера определите статистическую надежность результатов регрессионного моделирования. Выберите лучшее уравнение регрессии и дайте его обоснование.
Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
Оцените полученные результаты, выводы оформите в аналитической записке.
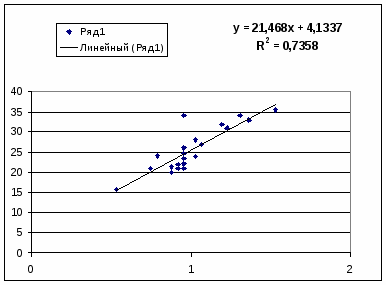
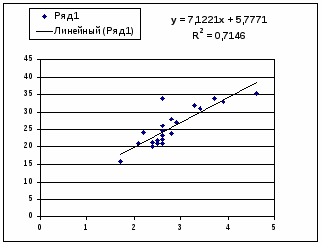
1. Поле корреляции для:
Линейной регрессии y=a+b*x:
Гипотеза о форме связи: чем больше размер среднедушевого денежного дохода в месяц (факторный признак), тем больше при прочих равных условиях розничная продажа телевизоров (результативный признак). В данной модели параметр b называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака у при отклонении величины факторного признаках на одну единицу.
Степенной регрессии
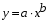 :
:
Гипотеза о форме связи: степенная функция имеет вид Y=axb.
Параметр b степенного уравнения называется показателем эластичности и указывает, на сколько процентов изменится у при возрастании х на 1%. При х = 1 a = Y.
Экспоненциальная регрессия
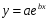 :
:
Равносторонняя гипербола
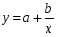 :
:
Гипотеза о форме связи: В ряде случаев обратная связь между факторным и результативным признаками может быть выражена уравнением гиперболы: Y=a+b/x.
Обратная гипербола
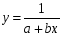 :
:
Полулогарифмическая регрессия
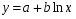 :
:
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
Рассчитаем параметры уравнений линейной парной регрессии. Для расчета параметров a и b линейной регрессии y=a+b*x решаем систему нормальных уравнений относительно a и b:
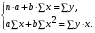
По исходным данным рассчитываем ∑y, ∑x, ∑yx, ∑x2, ∑y2 (табл. 2):
№ региона
X
Y
XY
X^2
Y^2
Y^cp
Y-Y^cp
Ai
1
2,800
28,000
78,400
7,840
784,000
25,719
2,281
0,081
2
2,400
21,300
51,120
5,760
453,690
22,870
-1,570
0,074
3
2,100
21,000
44,100
4,410
441,000
20,734
0,266
0,013
4
2,600
23,300
60,580
6,760
542,890
24,295
-0,995
0,043
5
1,700
15,800
26,860
2,890
249,640
17,885
-2,085
0,132
6
2,500
21,900
54,750
6,250
479,610
23,582
-1,682
0,077
7
2,400
20,000
48,000
5,760
400,000
22,870
-2,870
0,144
8
2,600
22,000
57,200
6,760
484,000
24,295
-2,295
0,104
9
2,800
23,900
66,920
7,840
571,210
25,719
-1,819
0,076
10
2,600
26,000
67,600
6,760
676,000
24,295
1,705
0,066
11
2,600
24,600
63,960
6,760
605,160
24,295
0,305
0,012
12
2,500
21,000
52,500
6,250
441,000
23,582
-2,582
0,123
13
2,900
27,000
78,300
8,410
729,000
26,431
0,569
0,021
14
2,600
21,000
54,600
6,760
441,000
24,295
-3,295
0,157
15
2,200
24,000
52,800
4,840
576,000
21,446
2,554
0,106
16
2,600
34,000
88,400
6,760
1156,000
24,295
9,705
0,285
17
3,300
31,900
105,270
10,890
1017,610
29,280
2,620
0,082
19
3,900
33,000
128,700
15,210
1089,000
33,553
-0,553
0,017
20
4,600
35,400
162,840
21,160
1253,160
38,539
-3,139
0,089
21
3,700
34,000
125,800
13,690
1156,000
32,129
1,871
0,055
22
3,400
31,000
105,400
11,560
961,000
29,992
1,008
0,033
Итого
58,800
540,100
1574,100
173,320
14506,970
540,100
0,000
сред значение
2,800
25,719
74,957
8,253
690,808
0,085
станд. откл
0,643
5,417
Система нормальных уравнений составит:
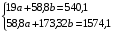
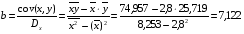
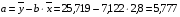
Ур-ие регрессии: = 5,777+7,122∙x. Данное уравнение показывает, что с увеличением среднедушевого денежного дохода в месяц на 1 тыс. руб. доля розничных продаж телевизоров повышается в среднем на 7,12%.
Рассчитаем параметры уравнений степенной парной регрессии. Построению степенной модели
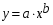 предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
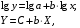 где
где 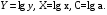
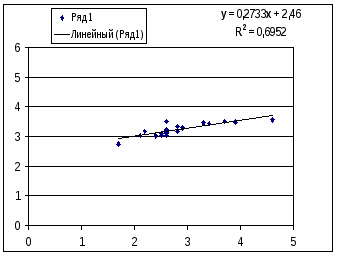
Для расчетов используем данные табл. 3:
№ рег
X
Y
XY
X^2
Y^2
Yp^cp
y^cp
1
1,030
3,332
3,431
1,060
11,104
3,245
25,67072
2
0,875
3,059
2,678
0,766
9,356
3,116
22,56102
3
0,742
3,045
2,259
0,550
9,269
3,004
20,17348
4
0,956
3,148
3,008
0,913
9,913
3,183
24,12559
5
0,531
2,760
1,465
0,282
7,618
2,827
16,90081
6
0,916
3,086
2,828
0,840
9,526
3,150
23,34585
7
0,875
2,996
2,623
0,766
8,974
3,116
22,56102
8
0,956
3,091
2,954
0,913
9,555
3,183
24,12559
9
1,030
3,174
3,268
1,060
10,074
3,245
25,67072
10
0,956
3,258
3,113
0,913
10,615
3,183
24,12559
11
0,956
3,203
3,060
0,913
10,258
3,183
24,12559
12
0,916
3,045
2,790
0,840
9,269
3,150
23,34585
13
1,065
3,296
3,509
1,134
10,863
3,275
26,4365
14
0,956
3,045
2,909
0,913
9,269
3,183
24,12559
15
0,788
3,178
2,506
0,622
10,100
3,043
20,97512
16
0,956
3,526
3,369
0,913
12,435
3,183
24,12559
17
1,194
3,463
4,134
1,425
11,990
3,383
29,4585
19
1,361
3,497
4,759
1,852
12,226
3,523
33,88317
20
1,526
3,567
5,443
2,329
12,721
3,661
38,90802
21
1,308
3,526
4,614
1,712
12,435
3,479
32,42145
22
1,224
3,434
4,202
1,498
11,792
3,408
30,20445
итого
21,115
67,727
68,921
22,214
219,361
67,727
537,270
сред зн
1,005
3,225
3,282
1,058
10,446
3,225
стан откл
0,216
0,211
Рассчитаем С и b:
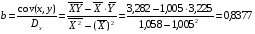
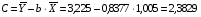
Получим линейное уравнение: 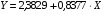 . Выполнив его потенцирование, получим:
. Выполнив его потенцирование, получим: 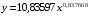
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата y.
Рассчитаем параметры уравнений экспоненциальной парной регрессии. Построению экспоненциальной модели
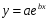 предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
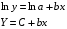 где
где 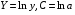
Для расчетов используем данные табл. 4:
№ региона
X
Y
XY
X^2
Y^2
Yp
y^cp
1
2,800
3,332
9,330
7,840
11,104
3,225
25,156
2
2,400
3,059
7,341
5,760
9,356
3,116
22,552
3
2,100
3,045
6,393
4,410
9,269
3,034
20,777
4
2,600
3,148
8,186
6,760
9,913
3,170
23,818
5
1,700
2,760
4,692
2,890
7,618
2,925
18,625
6
2,500
3,086
7,716
6,250
9,526
3,143
23,176
7
2,400
2,996
7,190
5,760
8,974
3,116
22,552
8
2,600
3,091
8,037
6,760
9,555
3,170
23,818
9
2,800
3,174
8,887
7,840
10,074
3,225
25,156
10
2,600
3,258
8,471
6,760
10,615
3,170
23,818
11
2,600
3,203
8,327
6,760
10,258
3,170
23,818
12
2,500
3,045
7,611
6,250
9,269
3,143
23,176
13
2,900
3,296
9,558
8,410
10,863
3,252
25,853
14
2,600
3,045
7,916
6,760
9,269
3,170
23,818
15
2,200
3,178
6,992
4,840
10,100
3,061
21,352
16
2,600
3,526
9,169
6,760
12,435
3,170
23,818
17
3,300
3,463
11,427
10,890
11,990
3,362
28,839
19
3,900
3,497
13,636
15,210
12,226
3,526
33,978
20
4,600
3,567
16,407
21,160
12,721
3,717
41,140
21
3,700
3,526
13,048
13,690
12,435
3,471
32,170
22
3,400
3,434
11,676
11,560
11,792
3,389
29,638
Итого
58,800
67,727
192,008
173,320
219,361
67,727
537,053
сред зн
2,800
3,225
9,143
8,253
10,446
стан откл
0,643
0,211
Рассчитаем С и b:
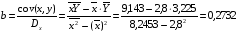
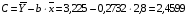
Получим линейное уравнение: 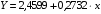 . Выполнив его потенцирование, получим:
. Выполнив его потенцирование, получим: 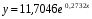
Для расчета теоретических значений y подставим в уравнение 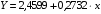 значения x.
значения x.
Рассчитаем параметры уравнений полулогарифмической парной регрессии. Построению полулогарифмической модели
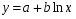 предшествует процедура линеаризации переменных. В примере линеаризация производится путем замены:
предшествует процедура линеаризации переменных. В примере линеаризация производится путем замены:
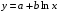 где
где 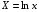
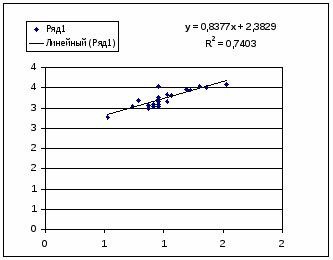
Для расчетов используем данные табл. 5:
№ региона
X
Y
XY
X^2
Y^2
y^cp
1
1,030
28,000
28,829
1,060
784,000
26,238
2
0,875
21,300
18,647
0,766
453,690
22,928
3
0,742
21,000
15,581
0,550
441,000
20,062
4
0,956
23,300
22,263
0,913
542,890
24,647
5
0,531
15,800
8,384
0,282
249,640
15,525
6
0,916
21,900
20,067
0,840
479,610
23,805
7
0,875
20,000
17,509
0,766
400,000
22,928
8
0,956
22,000
21,021
0,913
484,000
24,647
9
1,030
23,900
24,608
1,060
571,210
26,238
10
0,956
26,000
24,843
0,913
676,000
24,647
11
0,956
24,600
23,506
0,913
605,160
24,647
12
0,916
21,000
19,242
0,840
441,000
23,805
13
1,065
27,000
28,747
1,134
729,000
26,991
14
0,956
21,000
20,066
0,913
441,000
24,647
15
0,788
24,000
18,923
0,622
576,000
21,060
16
0,956
34,000
32,487
0,913
1156,000
24,647
17
1,194
31,900
38,086
1,425
1017,610
29,765
19
1,361
33,000
44,912
1,852
1089,000
33,351
20
1,526
35,400
54,022
2,329
1253,160
36,895
21
1,308
34,000
44,483
1,712
1156,000
32,221
22
1,224
31,000
37,937
1,498
961,000
30,406
Итого
21,115
540,100
564,166
22,214
14506,970
540,100
сред зн
1,005
25,719
26,865
1,058
690,808
стан откл
0,216
5,417
Рассчитаем a и b:
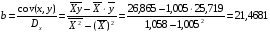
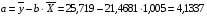
Получим линейное уравнение: 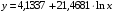 .
.
Рассчитаем параметры уравнений обратной парной регрессии. Для оценки параметров приведем обратную модель
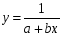 к линейному виду, заменив
к линейному виду, заменив 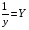 , тогда
, тогда 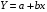
Для расчетов используем данные табл. 6:
№ региона
X
Y
XY
X^2
Y^2
Y^cp
1
2,800
0,036
0,100
7,840
0,001
24,605
2
2,400
0,047
0,113
5,760
0,002
22,230
3
2,100
0,048
0,100
4,410
0,002
20,729
4
2,600
0,043
0,112
6,760
0,002
23,357
5
1,700
0,063
0,108
2,890
0,004
19,017
6
2,500
0,046
0,114
6,250
0,002
22,780
7
2,400
0,050
0,120
5,760
0,003
22,230
8
2,600
0,045
0,118
6,760
0,002
23,357
9
2,800
0,042
0,117
7,840
0,002
24,605
10
2,600
0,038
0,100
6,760
0,001
23,357
11
2,600
0,041
0,106
6,760
0,002
23,357
12
2,500
0,048
0,119
6,250
0,002
22,780
13
2,900
0,037
0,107
8,410
0,001
25,280
14
2,600
0,048
0,124
6,760
0,002
23,357
15
2,200
0,042
0,092
4,840
0,002
21,206
16
2,600
0,029
0,076
6,760
0,001
23,357
17
3,300
0,031
0,103
10,890
0,001
28,398
19
3,900
0,030
0,118
15,210
0,001
34,844
20
4,600
0,028
0,130
21,160
0,001
47,393
21
3,700
0,029
0,109
13,690
0,001
32,393
22
3,400
0,032
0,110
11,560
0,001
29,301
Итого
58,800
0,853
2,296
173,320
0,036
537,933
сред знач
2,800
0,041
0,109
8,253
0,002
стан отклон
0,643
0,009
Рассчитаем a и b:
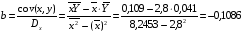
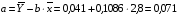
Получим линейное уравнение: 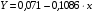 . Выполнив его потенцирование, получим:
. Выполнив его потенцирование, получим: 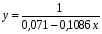
Для расчета теоретических значений y подставим в уравнение 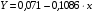 значения x.
значения x.
Рассчитаем параметры уравнений равносторонней гиперболы парной регрессии. Для оценки параметров приведем модель равносторонней гиперболы
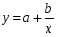 к линейному виду, заменив
к линейному виду, заменив 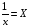 , тогда
, тогда 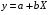
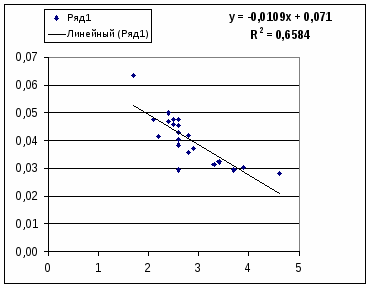
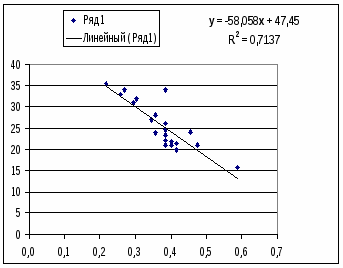
Для расчетов используем данные табл. 7:
№ региона
X=1/z
Y
XY
X^2
Y^2
Y^cp
1
0,357
28,000
10,000
0,128
784,000
26,715
2
0,417
21,300
8,875
0,174
453,690
23,259
3
0,476
21,000
10,000
0,227
441,000
19,804
4
0,385
23,300
8,962
0,148
542,890
25,120
5
0,588
15,800
9,294
0,346
249,640
13,298
6
0,400
21,900
8,760
0,160
479,610
24,227
7
0,417
20,000
8,333
0,174
400,000
23,259
8
0,385
22,000
8,462
0,148
484,000
25,120
9
0,357
23,900
8,536
0,128
571,210
26,715
10
0,385
26,000
10,000
0,148
676,000
25,120
11
0,385
24,600
9,462
0,148
605,160
25,120
12
0,400
21,000
8,400
0,160
441,000
24,227
13
0,345
27,000
9,310
0,119
729,000
27,430
14
0,385
21,000
8,077
0,148
441,000
25,120
15
0,455
24,000
10,909
0,207
576,000
21,060
16
0,385
34,000
13,077
0,148
1156,000
25,120
17
0,303
31,900
9,667
0,092
1017,610
29,857
19
0,256
33,000
8,462
0,066
1089,000
32,564
20
0,217
35,400
7,696
0,047
1253,160
34,829
21
0,270
34,000
9,189
0,073
1156,000
31,759
22
0,294
31,000
9,118
0,087
961,000
30,374
Итого
7,860
540,100
194,587
3,073
14506,970
540,100
сред знач
0,374
25,719
9,266
0,146
1318,815
стан отклон
0,079
25,639
Рассчитаем a и b:
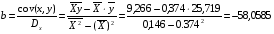
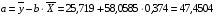
Получим линейное уравнение: 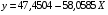 . Получим уравнение регрессии:
. Получим уравнение регрессии: 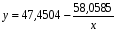 .
.
3. Оценка тесноты связи с помощью показателей корреляции и детерминации:
Линейная модель. Тесноту линейной связи оценит коэффициент корреляции. Был получен следующий коэффициент корреляции rxy=b=7,122*
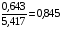 , что говорит о прямой сильной связи фактора и результата. Коэффициент детерминации r²xy=(0,845)²=0,715. Это означает, что 71,5% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
, что говорит о прямой сильной связи фактора и результата. Коэффициент детерминации r²xy=(0,845)²=0,715. Это означает, что 71,5% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.Степенная модель. Тесноту нелинейной связи оценит индекс корреляции. Был получен следующий индекс корреляции
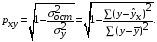 =
=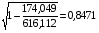 , что говорит о очень сильной тесной связи, но немного больше чем в линейной модели. Коэффициент детерминации r²xy=0,7175. Это означает, что 71,75% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
, что говорит о очень сильной тесной связи, но немного больше чем в линейной модели. Коэффициент детерминации r²xy=0,7175. Это означает, что 71,75% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.Экспоненциальная модель. Был получен следующий индекс корреляции ρxy=0,8124, что говорит о том, что связь прямая и очень сильная, но немного слабее, чем в линейной и степенной моделях. Коэффициент детерминации r²xy=0,66. Это означает, что 66% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
Полулогарифмическая модель. Был получен следующий индекс корреляции ρxy=0,8578, что говорит о том, что связь прямая и очень сильная, но немного больше чем в предыдущих моделях. Коэффициент детерминации r²xy=0,7358. Это означает, что 73,58% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
Гиперболическая модель. Был получен следующий индекс корреляции ρxy=0,8448 и коэффициент корреляции rxy=-0,1784 что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy=0,7358. Это означает, что 73,5% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
Обратная модель. Был получен следующий индекс корреляции ρxy=0,8114 и коэффициент корреляции rxy=-0,8120, что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy=0,6584. Это означает, что 65,84% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
Вывод: по полулогарифмическому уравнению получена наибольшая оценка тесноты связи: ρxy=0,8578 (по сравнению с линейной, степенной, экспоненциальной, гиперболической, обратной регрессиями).
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
Рассчитаем коэффициент эластичности для линейной модели:
Для уравнения прямой: y = 5,777+7,122∙x
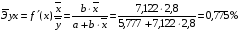
Для уравнения степенной модели
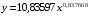 :
:
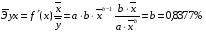
Для уравнения экспоненциальной модели
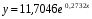 :
:
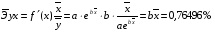
Для уравнения полулогарифмической модели 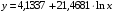 :
:
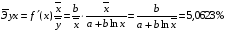
Для уравнения обратной гиперболической модели
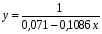 :
:
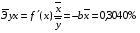
Для уравнения равносторонней гиперболической модели
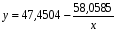 :
:
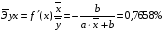
Сравнивая значения  , характеризуем оценку силы связи фактора с результатом:
, характеризуем оценку силы связи фактора с результатом:
Известно, что коэффициент эластичности показывает связь между фактором и результатом, т.е. на сколько% изменится результат y от своей средней величины при изменении фактора х на 1% от своего среднего значения. В данном примере получилось, что самая большая сила связи между фактором и результатом в полулогарифмической модели, слабая сила связи в обратной гиперболической модели.
5. Оценка качества уравнений с помощью средней ошибки аппроксимации.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения  . Найдем величину средней ошибки аппроксимации
. Найдем величину средней ошибки аппроксимации 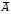 :
:
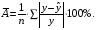
В среднем расчетные значения отклоняются от фактических на:
Линейная регрессия. =
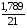 *100%= 8,5%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
*100%= 8,5%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как  не превышает 8 -10%.
не превышает 8 -10%.
Степенная регрессия. =
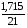 *100%= 8,2%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
*100%= 8,2%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как 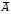 не превышает 8 -10%.
не превышает 8 -10%.
Экспоненциальная регрессия. =
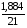 *100%= 9%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
*100%= 9%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как 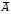 не превышает 8 -10%.
не превышает 8 -10%.
Полулогарифмическая регрессия. =
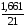 *100%= 7,9 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
*100%= 7,9 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как 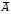 не превышает 8 -10%.
не превышает 8 -10%.
Гиперболическая регрессия. =
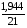 *100%= 9,3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
*100%= 9,3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как 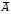 не превышает 8 -10%.
не превышает 8 -10%.
Обратная регрессия. =
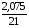 *100%= 9,9 3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
*100%= 9,9 3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как 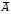 не превышает 8 -10%.
не превышает 8 -10%.
6. Рассчитаем F-критерий:
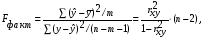
Линейная регрессия. =
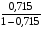 *19= 47,579
*19= 47,579
где =4,38<
Степенная регрессия. =
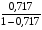 *19= 48,257
*19= 48,257
где =4,38<
Экспоненциальная регрессия. =
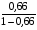 *19= 36,878
*19= 36,878
где =4,38<
Полулогарифмическая регрессия. =
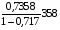 *19= 52,9232
*19= 52,9232
где =4,38<
Гиперболическая регрессия. =
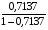 *19= 47,357
*19= 47,357
где =4,38<
Обратная регрессия. =
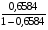 *19= 36,627
*19= 36,627
где =4,38<
Для всех регрессий =4,38< , из чего следует, что уравнения регрессии статистически значимы.
Вывод: остается на допустимом уровне для всех уравнений регрессий.
А
R^2
Fфакт
Линейная модель
8,5
0,714
47,500
Степенная модель
8,2
0,718
48,250
Полулогарифмическая модель
7,9
0,736
52,920
Экспоненциальная модель
9,0
0,660
36,870
Равносторонняя гипербола
9,3
0,714
47,350
Обратная гипербола
9,9
0,453
15,700
Все уравнения регрессии достаточно хорошо описывают исходные данные. Некоторое предпочтение можно отдать полулогарифмической функции, для которой значение R^2 наибольшее, а ошибка аппроксимации – наименьшая
7. Рассчитаем прогнозное значение результата по линейному уравнению регрессии, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определим доверительный интервал прогноза для уровня значимости α=0,05:
Прогнозное значение 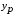 определяется путем подстановки в уравнение регрессии
определяется путем подстановки в уравнение регрессии 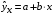 соответствующего (прогнозного) значения
соответствующего (прогнозного) значения 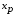 .
.
5,777+7,122*2,996=27,114
где = 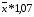 =2,8*1,07=2,996
=2,8*1,07=2,996
Средняя стандартная ошибка прогноза 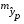 :
:
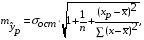 =
=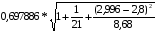 =3,12
=3,12
где 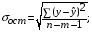 =
=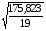 =0,697886
=0,697886
Предельная ошибка прогноза:
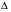
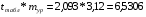
Доверительный интервал прогноза
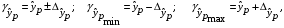 где
где 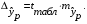
=27,116,53;
27,11–6,53 = 20,58
27,11+6,53 = 33,64
Выполненный прогноз среднедушевых денежных доходов в месяц, x оказался надежным (р = 1 – α = 1 – 0,05 = 0,95), но неточным, так как диапазон верхней и нижней границ доверительного интервала 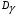 составляет 2,09 раза:
составляет 2,09 раза:
= =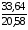 =1,63
=1,63

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ