Передаточная функция дискретной системы
































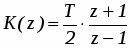
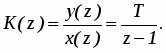
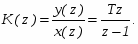
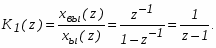
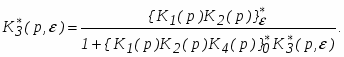
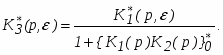
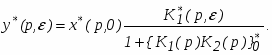
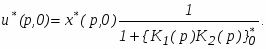
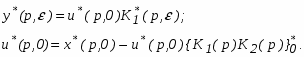
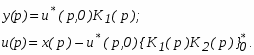
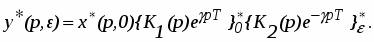
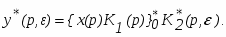
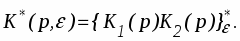
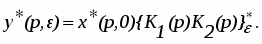
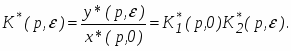
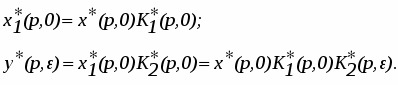

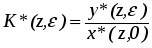
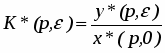
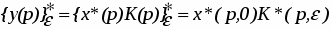
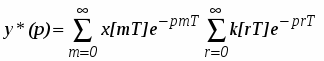
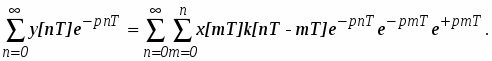

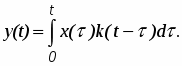
Предмет:
"Теория автоматического управления"
Тема:
"Передаточная функция дискретной системы"
1. Передаточные функции дискретных систем
Для непрерывных систем связь между выходом и входом определяется через интеграл свертки
(1)
Определим зависимость между входом и выходом для дискретной системы (рис. 1).
x(p) x*(p) y(p)
K(p)
x(t) x*(t) y(t)
T
T,
y*(p)
Рис. 1
При этом можно записать y(p) = x*(p) K(p). Это смешанное выражение оно бесполезно, так как математика не имеет методов определения таких оригиналов. Вводим фиктивный импульсный элемент с модификацией, при этом выходная величина также будет дискретной.
Если обозначить t = nT и = mT, то для выхода дискретной системы можно записать
(2)
Выполним дискретное преобразование
Если обозначить r = n-m и учесть, что при m > 0 k [nT-mT] = 0 а, следовательно, можно поменять пределы в суммах, то можно записать
. (3)
При этом можно записать
y*(p) = x*(p) K*(p), (4)
или для модифицированного преобразования
y*(p,) = x*(p, 0) K*(p,). (5)
Это выражение можно получить, выполнив операцию «звездочки» над смешанным выражением
Дискретная передаточная функция равна
или . (6)
Передаточная функция дискретной системы – это отношение дискретного преобразования выходной величины к дискретному преобразованию входной величины при нулевых начальных условиях.
2. Основы структурного метода для дискретных систем
Рассмотрим запись передаточных функций соединений динамических звеньев. Предположим, что соединение имеет несколько импульсных элементов работающих синхронно с одинаковым периодом.
Динамические звенья разделены импульсными элементами
Рассмотрим схему рис. 2.
x(p) x*(p) x1(p) x1*(p) y(p)
x(t) x*(t) x1(t) x1*(t) y(t)
y*(p, )
T,
K2(p)
T
K1(p)
T
Рис. 2
Для заданной схемы можно записать соотношения
При этом дискретная передаточная функция равна
(7)
Т.е. дискретная передаточная функция последовательного соединения, приведенного на рис. 2, равна произведению дискретных передаточных функций элементов соединения.
Динамические звенья не разделены импульсными элементами
Рассмотрим схему рис. 3.
x(p) x*(p) x1(p) y(p)
x(t) x*(t) x1(t) y(t)
y*(p, )
T,
K2(p)
K1(p)
T
Рис. 3
Для заданной схемы можно записать соотношение
При этом дискретная передаточная функция равна
(8)
Т.е. для записи передаточной функции такого соединения необходимо вначале найти результирующую передаточную функцию, а затем перевести ее в дискретную форму.
3. Входной сигнал не квантуется
Рассмотрим схему рис.
x(t) x1(t) x1*(t) y(t)
x(p) x1(p) x1*(p) y(p)
y*(p, )
T,
K2(p)
T
K1(p)
Рис. 4
Для выхода соединения можно записать соотношение
(9)
Если входной сигнал не проходит через импульсный элемент, то записать передаточную функцию такого соединения нельзя, но можно записать выражение для выходной величины.
4. Соединение, в котором импульсные элементы работают асинхронно
Рассмотрим схему рис. 5.
x(p) ИЭ1 x*(p) x1(p) ИЭ2 x1*(p) y(p)
x(t) x*(t) x1(t) x1*(t) y(t)
y*(p, )
T,
K2(p)
T
K1(p)
T
Рис. 5
Диаграммы работы ИЭ приведены на рис. 6.
ИЭ
2
T
t
ИЭ1
T
t
T
Рис. 6
Исходную схему можно привести к эквивалентной синхронной (рис. 7).
x(p) K1(p) ejT e-jT K2(p) y(p)
T T y*(p, )
T,
ИЭ1 ИЭ2
t T 1 ИЭ
Рис. 7
Для выхода соединения можно записать соотношение
(10)
5. Передаточные функции дискретных систем с обратной связью
Рассмотрим схему рис. 7.
x(p) u(p) u*(p)
K1(p) y(p)
T
Y*(p,)
K2(p) T,
Рис. 7
Порядок расчета передаточной функции дискретной системы с обратной связью.
Ставим на выходе системы фиктивный импульсный элемент.
2. Разрываем цепь на месте ИЭ и записываем уравнение для выхода системы и входа ИЭ
От смешанных уравнений переходим к дискретным
Находим
Подставим это в исходное уравнение
6. Передаточная функция
Пример 1. Записать передаточную функцию дискретной системы, схема которой приведена на рис. 8.
k x(p) y(p) K1(p) K2(p) - T y*(p,) K3(p) K4(p) T T,
Рис. 8
Передаточная функция имеет вид
6. Передаточные функции цифровых алгоритмов
В дискретных системах с программной реализацией алгоритмов управления используются методы цифрового интегрирования. При этом передаточная функция алгоритма управления зависит от метода численного интегрирования и формы экстраполирования. Чаще всего используются методы прямоугольников, трапеций и Симпсона, которые содержат минимальное арифметических операций в алгоритме реализации, а в качестве фиксирующего звена используют фиксатор нулевого порядка.
Программную реализацию алгоритмов управления называют дискретной коррекцией. Каждой дискретной передаточной функции соответствует определенный алгоритм и наоборот.
Рассмотрим дискретную систему (рис. 9).
x(t) АЦП ЦА ЦАП K(p) y(t)
Рис. 9
Данную схему можно представить в виде (рис. 10)
x(t) (1-e-pT) K(p) y(t)
T T p
K1(z)
Рис. 10
Допустим, задан алгоритм функционирования ЦА (рис. 11)
X вх [kT] ЦА xвых[kT]
x
Рис. 11
xвых[kT] = xвых[kT-T]+xвх[kT-T]. (11)
В соответствии с разностным уравнением, запишем операторное уравнение в форме z – преобразования:
xвых(z) = z -1 xвых(z) + z -1xвх(z). (12)
При этом передаточная функция цифрового алгоритма имеет вид:
(13)
Алгоритмы цифрового интегрирования
Передаточная функция алгоритма интегрирования по методу прямоугольников зависит от выбранного метода прямоугольной аппроксимации сигнала (рис. 12а, б).
В соответствии с рис. 12а, можно записать уравнение
y[kT]=y [kT-T]+x[kT] T, (14)
где y[kT], y [kT-T] – текущее и предыдущее значение интеграла;
x[kT] T – приращение.
При этом передаточная функция алгоритма имеет вид
(15)
В соответствии с рис 12б, можно записать уравнение
y[kT]=y [kT-T]+x [kT-T] T, (16)
где y[kT], y [kT-T] – текущее и предыдущее значение интеграла;
x [kT-T] T – приращение.
При этом передаточная функция алгоритма имеет вид
(17)
x[nT]
0 kT-T kT nT
а)
x[nT]
0 kT-T kT nT б)
Рис. 12
Интегрирование по методу трапеций
При интегрировании по методу трапеций (рис 13) можно записать уравнение
y[kT]=y [kT-T]+(x [kT-T]+x[kT]) T/2, (18)
где y[kT], y [kT-T] – текущее и предыдущее значение интеграла;
(x [kT-T]+x[kT]) T/2 – приращение.
0 kT-T kT nT
Рис. 13
x[nT]
Применив z – преобразование к уравнению (18), получим выражение для передаточной функции при трапецеидальной аппроксимации входного сигнала.
. (19)
Литература
Бронштейн И.Н., Семендяев К.Н. Справочник по математике для инженеров и учащихся вузов. – М.: Наука, 1986.
Дорф Р., Бишоп Р. Автоматика. Современные системы управления. 2002 г. – 832 с.
Харазов В.Г. Интегрированные системы управления технологическими процессами: Справочник. Издательство: ПРОФЕССИЯ, ИЗДАТЕЛЬСТВО, 2009. – 550 с.
Чебурахин И. Синтез дискретных управляющих систем и математическое моделирование: теория, алгоритмы, программы. Изд-во: НИЦ РХД, ФИЗМАТЛИТ, 2004. – 248c.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ