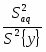
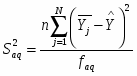
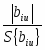
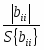
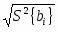
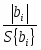
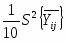
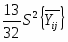
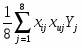
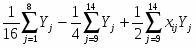
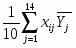
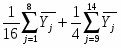
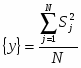
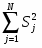
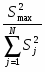
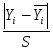
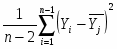
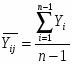
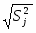
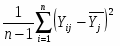
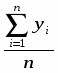
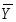
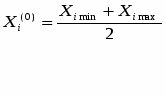Федеральное агентство по образованию

ГОУ ВПО

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

Факультет: Механической технологии древесины

Кафедра: Технологии композиционных материалов и древесиноведения

Планы второго порядка. Реализация В₃-плана

Реферат

В данном курсовом проекте содержится разработка метода планирования второго порядка на примере В₃-плана, получение и исследование математической модели объекта в виде полинома второго порядка, статистический анализ полученного уравнения и построение поверхностей отклика.

Пояснительная записка содержит: листов машинописного текста, 7 таблиц, рисунков, 1 библиографического наименования.

Содержание

Реферат

Введение

1 Расчетная часть

1.1 Значение и анализ выходной величины

1.2 Статистический анализ полученных данных

1.2.1. Проверка на наличие грубых измерений

1.2.2 Проверка однородности дисперсий

1.2.3 Расчет дисперсии воспроизводимости

2 Построение математической модели

2.1 Расчет коэффициентов регрессии

2.2 Расчет дисперсий коэффициентов регрессии

2.3 Проверка значимости коэффициентов регрессии

2.4 Проверка модели на адекватность

2.5 Построение графической зависимости

Заключение

Список использованных источников

Введение

Важное место в повышении уровня исследований в деревообрабатывающей промышленности занимают вопросы математического планирования эксперимента.

Математическая теория эксперимента предполагает многофакторный, системный, вероятностно-статистический подход исследований процессов и явлений.

Научный подход к обработке результатов наблюдений составляет предмет изучения математической статистики. Математическая статистика - это наука о математических методах обработки, систематизации и использовании результатов наблюдений для научных и практических выводов.

Методы математической статистики в настоящее время проникли во все области научных исследований, от физики и химии до экономики и социологии. Это объясняется тем, что каждая наука нуждается в анализе и обработке добытых ею факторов.

Роль математической статистики в исследовании лесной и деревообрабатывающей промышленности особенно велика. Для предмета труда этой области промышленности – древесины - характерно большое разнообразие характеристик. Поэтому, проведение научных исследований в лесной и деревообрабатывающей промышленности всегда связано с большим числом наблюдений, результаты которых обрабатывают при помощи методов математической статистики.

Цель курсовой работы: получение и исследование математической модели объекта в виде полинома второго порядка, статистический анализ полученного уравнения и построение поверхностей отклика.

1 Расчетная часть

1.1 Значение и анализ выходной величины.

Исследование зависимости посылки по мощности привода от некоторых технологических факторов.

В рассматриваемом частном случае реализации В₃ – плана участвуют три основных фактора, каждый из которых имеет диапазон варьирования:

X_1min11max

X_2min22max (1.1)

X_3min<X₃<X_3max

Основной уровень или середину диапазона выравнивания находим из соотношения:

. (1.2)

Уровни варьирования переменных факторов занесем в таблицу 1.1

Таблица 1.1 – Переменные факторы и уровни их варьирования

Наименование факторов

Обозначения факторов

Уровни варьирования

верхний +1

основной

0

нижний

-1

1. Диаметр распиливаемых бревен, d, см

X₁

56

48

40

2. Толщина бруса, Н, мм

X₂

225

175

125

3. Количество сечений, m, шт

X₃

9

7

5

В результате проведенных опытов получены значения выходных величин и проведен первичный анализ.

Среднее значение выходной величины рассчитывается по формуле:

_j=, (1.3)

где n – количество опытов.

Выборочные дисперсии по каждому опыту рассчитываются по следующей формуле:

S_j²=. (1.4)

Среднеквадратическое отклонение:

S_j=. (1.5)

Полученные данные занесем в таблицу 1.2

Таблица 1.2 – Значения выходных величин

Номер опыта

Заданные значения выходной величины

Анализ выходной величины

Y_1j

Y_2j

Y_3j

Y_4j

Y_5j

Y_jj

S_jj²

S_ij

1

17

15.6

17.7

14.5

15.3

16.02

1.697

1.30269

2

29.4

38.5

37.4

33.8

29.2

33.66

18.868

4.343731

3

14.9

11.2

14.9

12.8

11.7

13.1

3.035

1.742125

4

28.7

26.6

27.9

24

29.6

27.36

4.743

2.177843

5

35

33

38.5

28.7

31.7

33.38

13.427

3.664287

6

67.5

51.8

52.9

62.3

62.1

59.32

45.322

6.732162

7

36.8

31.6

39

33.9

32.5

34.76

9.493

3.081071

8

53.3

58.1

53.5

62.3

56.9

56.82

13.772

3.711065

9

20.8

19.5

21.1

18

17.7

19.42

2.427

1.557883

10

35.4

42.7

42.5

37.3

36.9

38.96

11.548

3.398235

11

33.1

35

32.3

26.2

26.3

30.58

16.587

4.072714

12

28.1

24.7

28.8

26.1

27.8

27.1

2.785

1.668832

13

23.9

24.8

25.7

23.3

20.4

23.62

4.067

2.01668

14

48.2

46.2

45.9

55

48.9

48.84

13.493

3.673282

1.2 Статистический анализ полученных данных

1.2.1 Проверка на наличие грубых измерений

Наличие дублированных опытов можно оценить имеющиеся выборки по каждому опыту на предмет грубых измерений (табл. 1.3). Для этого сомнительный результат исключают из выборки.

По оставшимся данным вычисляют (табл. 1.4):

• среднее арифметическое:

, (1.6)

где i=1…4; j=1…14.

• оценка дисперсии:

S_j²=. (1.7)

Таблица 1.3 – Проверка на наличие промахов

Номер опыта

Заданные значения выходной величины

Анализ выходной величины

Y_1j

Y_2j

Y_3j

Y_4j

Y_5j

Y_jj

S_jj²

S_ij

1

17

15.6

17.7

14.5

15.3

16.02

1.697

1.30269

2

29.4

38.5

37.4

33.8

29.2

33.66

18.868

4.343731

3

14.9

11.2

14.9

12.8

11.7

13.1

3.035

1.742125

4

28.7

26.6

27.9

24

29.6

27.36

4.743

2.177843

5

35

33

38.5

28.7

31.7

33.38

13.427

3.664287

6

67.5

51.8

52.9

62.3

62.1

59.32

45.322

6.732162

7

36.8

31.6

39

33.9

32.5

34.76

9.493

3.081071

8

53.3

58.1

53.5

62.3

56.9

56.82

13.772

3.711065

9

20.8

19.5

21.1

18

17.7

19.42

2.427

1.557883

10

35.4

42.7

42.5

37.3

36.9

38.96

11.548

3.398235

11

33.1

35

32.3

26.2

26.3

30.58

16.587

4.072714

12

28.1

24.7

28.8

26.1

27.8

27.1

2.785

1.668832

13

23.9

24.8

25.7

23.3

20.4

23.62

4.067

2.01668

14

48.2

46.2

45.9

55

48.9

48.84

13.493

3.673282

Затем, определяется расчетное значение t – критерия Стьюдента для сомнительного результата

t_расч=. (1.8)

Таблица 1.4 – Результаты проверки наличия промахов

Номер опыта

Сомнительный элемент

Статистики для усеченной выборки

Расчетное значение критерия Стьюдента, tрасч

Yjj

Sjj²

Sjj

1

17.7

15.6

1.086666667

1.042433051

2.01451786

2

38.5

32.45

15.39666667

3.923858645

1.54184963

3

11.2

13.575

2.5425

1.594521872

-1.489474708

4

29.6

26.8

4.233333333

2.057506582

1.360870495

5

38.5

32.1

6.98

2.641968963

2.422435725

6

67.5

57.275

32.54916667

5.705187698

1.792228502

7

36.8

34.25

10.92333333

3.305046646

0.771547356

8

62.3

55.45

5.85

2.418677324

2.83212644

9

17.7

19.85

2.003333333

1.415391583

-1.519014261

10

42.7

38.025

9.569166667

3.093406968

1.51127868

11

35

29.475

13.97583333

3.738426585

1.477894476

12

24.7

27.7

1.313333333

1.146007563

-2.617783772

13

25.7

23.1

3.62

1.902629759

1.366529661

14

55

47.3

2.18

1.476482306

5.215098053

По выбранному уровню значимости (q=0,05) и числу степеней свободы (f=3) находим табличное значение критерия (t_qf) [1. табл. Д1].

t_табл=3,18

t_расч.<t_qf .

1.2.2 Проверка однородности дисперсий

Проверку однородности дисперсий при полученном виде дублирования проводят с помощью G – критерия Кохрена:

G_расч=, (1.11)

где - сумма всех дисперсий;

S²_max – наибольшая из всех найденных дисперсий.

G_расч=13,98/112,22= 0,125

При q=0,05 и f=n-1=3, G_табл=0,29 [1. табл. Ж1].

Так как G_расч <G_табл, то гипотеза об однородности дисперсии опытов принимается.

1.2.3 Расчет дисперсии воспроизводимости

Дисперсия воспроизводимости определяется по формуле:

S^{2 ,} (1.12)

где N- число опытов.

S²{y}=112,22/14= 8,02

Число степеней свободы для данной процедуры:

f_y=N(n-1) (1.13)

f_y=3*14=42.

2 Построение математической модели

2.1 Расчет коэффициентов регрессии

По результатам В₃-план построим математическую модель:

Y=b₀+b₁*x₁+b₂*x₂+b₃*x₃+b₁₁*x₁²+b₂₂*x₂²+b₃₃*x₃²+b₁₂*x₁*x₂+b₁₃*x₁*x₃+b₂₃*x₂*x₃

Таблица 2.1 – Матрица для расчета коэффициентов регрессии

№ опыта

X0

X1

X2

X3

X11

X22

X33

X12

X13

X23

Yij

Ŷij

1

2

3

4

5

6

7

8

9

10

11

12

13

1

1

1

1

1

1

1

1

1

1

1

16.02

15.92

2

1

-1

1

1

1

1

1

-1

-1

1

33.66

33.60

3

1

1

-1

1

1

1

1

-1

1

-1

13.1

12.95

4

1

-1

-1

1

1

1

1

1

-1

-1

27.36

27.00

5

1

1

1

-1

1

1

1

1

-1

-1

33.38

33.74

6

1

-1

1

-1

1

1

1

-1

1

-1

59.32

59.47

7

1

1

-1

-1

1

1

1

-1

-1

1

34.76

34.82

8

1

-1

-1

-1

1

1

1

1

1

1

56.82

56.92

9

1

1

0

0

1

0

0

0

0

0

19.42

19.25

10

1

-1

0

0

1

0

0

0

0

0

38.96

39.13

11

1

0

1

0

0

1

0

0

0

0

30.58

30.22

12

1

0

-1

0

0

1

0

0

0

0

27.1

27.46

13

1

0

0

1

0

0

1

0

0

0

23.62

24.29

14

1

0

0

-1

0

0

1

0

0

0

48.84

48.17

Используя матрицу базисных функций, табл. 2.1, коэффициенты регрессии определяем по следующим формулам:

- свободного члена:

b₀=-; (2.1)

- линейных коэффициентов регрессии:

b_i= ; (2.2)

- квадратичных коэффициентов:

b_ii = ; (2.3)

- коэффициентов при парных взаимодействиях:

b_iu= . (2.4)

2.2 Расчет дисперсий коэффициентов регрессии

Формулы для определения дисперсий: - дисперсия оценки свободного члена:

S²{b₀}= ; (2.5)

S²{b₀}=3,26

- дисперсия оценки линейных коэффициентов регрессии:

S²{b_i}= ; (2.6)

S²{b_i}=0,80

- дисперсия оценки квадратичных коэффициентов регрессии:

S²{b_ij}=; (2.7)

S²{b_ii}=3,26

- дисперсия оценки коэффициентов при парных взаимодействиях:

S²{b_iu}= . (2.8)

S²{b_iu}=1,00

2.3 Проверка значимости коэффициентов регрессии

Для оценки значимости регрессии используем t – критерий Стьюдента. По следующим формулам определяются расчетные значения t – критерия Стьюдента:

t_расчi=, (2.9)

где S{b_i}= - среднеквадратическое отклонение соответствующих дисперсий коэффициентов регрессии;

t_расчii=, (2.10)

t_расчiu=. (2.11)

Таблица 2.2 - Проверка значимости коэффициентов регрессии

обозначение коэффициентов регрессии

значение коэффициентов регрессии

Расчетные значения t-критерия Стьюдента

b₀

29.98

9

b₁

-9.94

-12

b₂

1.38

2

b₃

-11.94

-15

b₁₁

-0.79

0

b₂₂

-1.14

0

b₃₃

6.25

2

b₁₂

-0.91

-1

b₁₃

2.01

2

b₂₃

1.01

1

По t – критерию Стьюдента, по заданному уровню значимости (q=0,05) и числу степеней свободы (f_y=42), связанному с дисперсией воспроизводимости, находим табличное значение t – критерия Стьюдента [1. табл. Д1]:

t_табл =2,02

Если t_расч, > t_табл, то соответствующий коэффициент регрессии значим. Незначимые коэффициенты регрессии должны быть исключены из математической модели. Однако, в данной расчетной части с целью сохранения единообразия расчетов процедура исключения не проводится.

Получена следующая математическая модель в нормализованных обозначениях факторов:

Y=101,65+42,425х₁+2,9х₂+15,5х₃+8,4х₁₁-2,98х₂₂-2,46х₃₃₊2,22х1х2+6,28х1х3+1,11х₂х₃

2.4 Проверка модели на адекватность

Для проверки адекватности модели используют дисперсию адекватности S²_aq, процедура расчета которой зависит от вида дублирования опытов. Так как в нашем случае дублирование равномерное, то дисперсия адекватности рассчитывается по формуле:

(2.12)

где f_aq=N-p=14-10=4,

где p – число оцениваемых коэффициентов;

S²_aq= 0,39

Затем, по F – критерию Фишера для уровня значимости q=0,05 проверяется однородность S²_aq дисперсии адекватности (с числом степеней свободы f_aq):

F_расч= (2.13)

F_расч= 0,39/8,02=0,049

По таблице значения F - критерия Фишера [1. табл. Е1]:

F_табл=2,84. Так как F_табл.>F_расч, следовательно, найденную модель можно считать адекватной.

Таблица 2.3 – Математическая модель

Номер опыта

Факторы в натуральных обозначениях

Значение выходной величины

X₁, d, см

X₂, Н, мм

X₃ , m, шт

опытное

модельное

1

56

225

9

15.9055

15.9220

2

40

225

9

32.0175

33.6000

3

56

125

9

13.7255

12.9480

4

40

125

9

26.3175

26.9960

5

56

225

5

33.0255

33.7440

6

40

225

5

57.4575

59.4720

7

56

125

5

34.8455

34.8200

8

40

125

5

55.7575

56.9180

9

56

175

7

19.3855

19.2460

10

40

175

7

37.8975

39.1340

11

48

225

7

29.1295

30.2220

12

48

125

7

27.1895

27.4580

13

48

175

9

24.0095

24.2940

14

48

175

5

47.2895

48.1660

Уравнение регрессии в натуральных обозначениях факторов следующее:

Y=193,2-0,53d+0,23H-35,65m-0,012d²-0,0005H²+1,56m²-0,0022dH+0,13dm+0,01Hm

Таблица 2.4 – Значения выходной величины.

X1X2

40

44

48

52

56

125

162.738

155.4855

147.85

139.83

131.426

150

162.85

155.378

147.522

139.282

130.658

175

162.338

154.6455

146.57

138.11

129.266

200

161.2

153.288

144.992

136.312

127.248

225

159.438

151.3055

142.79

133.89

124.606

Таблица 2.5 – Значения выходной величины.

X1X3

40

44

48

52

56

5

-90.45

-99.202

-108.34

-117.86

-127.76

6

-148.46

-157.732

-158.03

-177.43

-187.85

7

-209.59

-219.382

-207.72

-240.12

-251.06

8

-273.84

-284.152

-257.41

-305.93

-317.39

9

-341.21

-352.042

-307.1

-374.86

-386.84

Таблица 2.6 – Значения выходной величины.

X2X3

125

150

175

200

225

5

81.1375

84.7

87.6375

89.95

91.6375

6

63.8975

67.71

70.8975

73.46

75.3975

7

49.7775

53.84

57.2775

60.09

62.2775

8

38.7775

43.09

46.7775

49.84

52.2775

9

30.8975

35.46

39.3975

42.71

45.3975

2.5 Построение графической зависимости

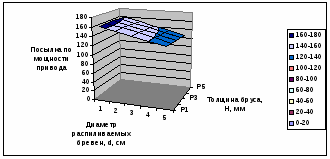
Рисунок 2.1 – Зависимость посылки по мощности привода от диаметра распиливаемых бревен и толщины бруса.

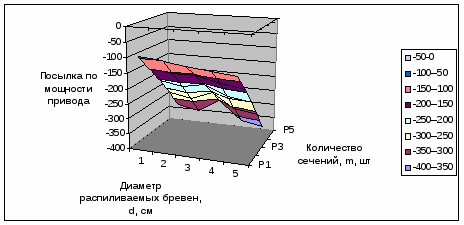
Рисунок 2.2 – Зависимость посылки по мощности привода от диаметра распиливаемых бревен и количества сечений.

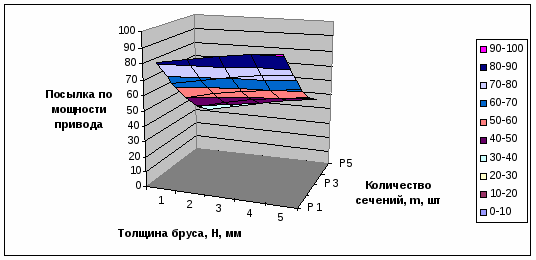
Рисунок 2.3 – Зависимость посылки по мощности привода от толщины бруса и количества сечений.

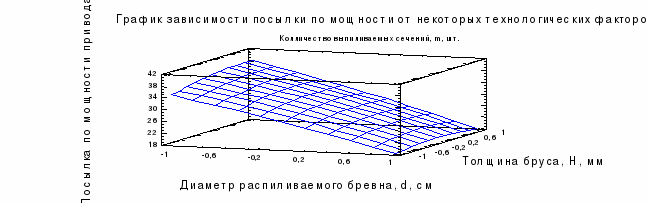
Рисунок 2.4 – График зависимости посылки по мощности привода от некоторых технологических факторов.

Заключение

В ходе выполнения курсовой работы мы изучили методы планирования второго порядка на примере В₃ плана, получили и исследовали математическую модель объекта в виде полинома второго порядка, провели статистический анализ полученного уравнения.

Анализируя полученную модель, получаем, что значимыми являются все три фактора.

Полученная модель позволяет предсказать значения выходной величины для любой точки внутри области варьирования факторов.

В результате расчета было получено, что различие между дисперсиями незначимо, следовательно, можно считать найденную модель объекта адекватной.

Список использованных источников

1. Л.Л. Кротова и др. Научные исследования в деревообработке. Планы второго порядка. Реализация В₃ плана. Учебное пособие по выполнению курсовой работы студентов специальности 250200 всех форм обучения/Л. Л. Кротова, А. А. Филлиповч, В. Ю. Буданов. - Красноярск: СибГТУ, 2003.-36с.