по Эконометрике 2
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КОНТРОЛЬНАЯ РАБОТА №1
По дисциплине: эконометрика
Вариант №1
Выполнил:
студент БУ,А и А
курс 3 2/в
Проверил: проф.
Сахабетдинов М.А.
Уфа – 2008
ЗАДАЧА 1. Экономическое моделирование стоимости квартир в Московской области.
1. Рассчитайте матрицу парных коэффициентов корреляции; оцените статистическую значимость коэффициентов корреляции.
2. Постройте поле корреляции результативного признака и наиболее тесно связанного с ним фактора.
3. Рассчитайте параметры линейной парной регрессии для всех факторов X.
4. Оцените качество каждой модели через коэффициент детерминации, среднюю ошибку аппроксимации и F-критерий Фишера. Выберите лучшую модель.
5. Осуществите прогнозирование для лучшей модели среднего значения показателя У при уровне значимости а = 0.1, если прогнозное значение фактора Х составит 80% от его максимального значения. Представьте графически: фактические и модельные значения, точки прогноза.
6. Используя пошаговую множественную регрессию (метод исключения или метод включения), постройте модель формирования цены квартиры за счет значимых факторов. Дайте экономическую интерпретацию коэффициентов модели регрессии.
7. Оцените качество построенной модели. Улучшилось ли качество модели по сравнению с однофакторной моделью? Дайте оценку влияния значимых факторов на результат с помощью коэффициентов эластичности, β- и ∆-коэффициентов.
Обозначения
У – цена квартиры, тыс. долл.
Х1 – город области
Х3 – общая площадь квартиры, кв.м.
Х5 – этаж квартиры
Данные:
n
У
Х1
Х3
Х5
1
115
0
70,4
9
2
85
1
82,8
5
3
69
1
64,5
6
4
57
1
55,1
1
5
184,6
0
83,9
1
6
56
1
32,2
2
7
85
0
65
12
8
265
0
169,5
10
9
60,65
1
74
11
10
130
0
87
6
11
46
1
44
2
12
115
0
60
2
13
70,96
0
65,7
5
14
39,5
1
42
7
15
78,9
0
49,3
14
16
60
1
64,5
11
17
100
1
93,8
1
18
51
1
64
6
19
157
0
98
2
20
123,5
1
107,5
12
21
55,2
0
48
9
22
95,5
1
80
6
23
57,6
0
63,9
5
24
64,5
1
58,1
10
25
92
1
83
9
26
100
1
73,4
2
27
81
0
45,5
3
28
65
1
32
5
29
110
0
65,2
10
30
42,1
1
40,3
13
31
135
0
72
12
32
39,6
1
36
5
33
57
1
61,6
8
34
80
0
35,5
4
35
61
1
58,1
10
36
69,6
1
83
4
37
250
1
152
15
38
64,5
1
64,5
12
39
125
0
54
8
40
152,3
0
89
7
Сумма
3746,0
23,0
2768,3
282,0
Ср.знач.
93,7
0,58
69,2
7,1
Задание 1. Рассчитайте матрицу парных коэффициентов корреляции; оцените статистическую значимость коэффициентов корреляции.
n
У2
Х12
Х32
Х52
У * Х1
У * Х3
У * Х5
X1* X3
X1 * X5
X3 * X5
1
13225
0
4956
81
0
8096
1035
0
0
633,6
2
7225
1
6856
25
85
7038
425
82,8
5
414
3
4761
1
4160
36
69
4451
414
64,5
6
387
4
3249
1
3036
1
57
3141
57
55,1
1
55,1
5
34077
0
7039
1
0
15488
185
0
0
83,9
6
3136
1
1037
4
56
1803
112
32,2
2
64,4
7
7225
0
4225
144
0
5525
1020
0
0
780
8
70225
0
28730
100
0
44918
2650
0
0
1695
9
3678
1
5476
121
61
4488
667
74
11
814
10
16900
0
7569
36
0
11310
780
0
0
522
11
2116
1
1936
4
46
2024
92
44
2
88
12
13225
0
3600
4
0
6900
230
0
0
120
13
5035
0
4316
25
0
4662
355
0
0
328,5
14
1560
1
1764
49
40
1659
277
42
7
294
15
6225
0
2430
196
0
3890
1105
0
0
690,2
16
3600
1
4160
121
60
3870
660
64,5
11
709,5
17
10000
1
8798
1
100
9380
100
93,8
1
93,8
18
2601
1
4096
36
51
3264
306
64
6
384
19
24649
0
9604
4
0
15386
314
0
0
196
20
15252
1
11556
144
124
13276
1482
107,5
12
1290
21
3047
0
2304
81
0
2650
497
0
0
432
22
9120
1
6400
36
96
7640
573
80
6
480
23
3318
0
4083
25
0
3681
288
0
0
319,5
24
4160
1
3376
100
65
3747
645
58,1
10
581
25
8464
1
6889
81
92
7636
828
83
9
747
26
10000
1
5388
4
100
7340
200
73,4
2
146,8
27
6561
0
2070
9
0
3686
243
0
0
136,5
28
4225
1
1024
25
65
2080
325
32
5
160
29
12100
0
4251
100
0
7172
1100
0
0
652
30
1772
1
1624
169
42
1697
547
40,3
13
523,9
31
18225
0
5184
144
0
9720
1620
0
0
864
32
1568
1
1296
25
40
1426
198
36
5
180
33
3249
1
3795
64
57
3511
456
61,6
8
492,8
34
6400
0
1260
16
0
2840
320
0
0
142
35
3721
1
3376
100
61
3544
610
58,1
10
581
36
4844
1
6889
16
70
5777
278
83
4
332
37
62500
1
23104
225
250
38000
3750
152
15
2280
38
4160
1
4160
144
65
4160
774
64,5
12
774
39
15625
0
2916
64
0
6750
1000
0
0
432
40
23195
0
7921
49
0
13555
1066
0
0
623
Сумма
454221
23
222656
2610
1748
307179
27583
1546
163
20523
Ср.знач.
11355,5
0,58
5566,4
65,3
43,7
7679,5
689,6
38,7
4,1
513,1
Расчет среднеквадратических отклонений:
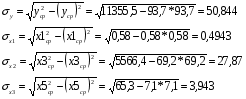
Расчет парных коэффициентов корреляции произведем по формуле:
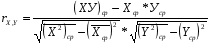
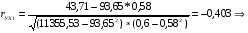связь между У и Х1 заметная, т.к. 0,3 < rух1 < 0,7.
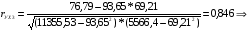связь между У и Х3 заметная, т.к. 0,3 < rух3 < 0,7.
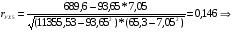связь между У и Х5 тесная, т.к. 0,7 < rух5 < 0,9.
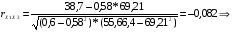связь между Х1 и Х3 слабая, т.к. 0,1 < rх1х3 < 0,3.
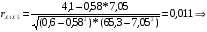связь между Х1 и Х5 слабая, т.к. 0,1 < rх1х5 < 0,3.
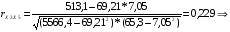связь между Х3 и Х5 весьма тесная, т.к. 0,9 < rх3х5 < 0,99.
Матрица парных коэффициентов корреляции:
1 rуx1 rуx2 rуx3
А = rуx1 1 rx1x2 rx1x3 
rуx2 rx1x2 1 rx2x3
rуx3 rx1x3 rx2x3 1
1 -0,403 0,846 0,146
А = -0,403 1 -0,082 0,011
0,846 -0,082 1 0,229
0,146 0,011 0,229 1
Используя функцию "Корреляция" в арсенале M. Excel, рассчитаем матрицу автоматически:
У
Х1
Х3
Х5
У
1
Х1
-0,403
1
Х3
0,846
-0,082
1
Х5
0,146
0,011
0,229
1
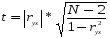Построим матрицу t - статистики парных коэффициентов корреляции, вычисленная по формуле:
Табличное значение t - критерия при 5% уровне значимости и степени свободы k = 40 – 1 – 1 = 38 составляет 2,03.
Если tухj > 2.03 => коэффициент корреляции между факторами у и хj статистически значим.
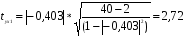> 2,03 → коэф-т корреляции между факторами у и х1 значим.
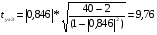> 2,03 → коэф-т корреляции между факторами у и х3 значим.
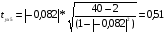< 2,03 → коэф-т корреляции между факторами у и х5 незначим.
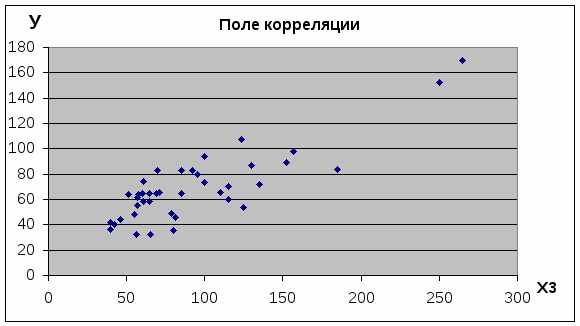
Очевидно, что наиболее сильная корреляция (связь) имеется между У - Х3.
Рассмотрим матрицу парных коэффициентов корреляции между факторами Хj. В нашем случае, явление сильной мультиколлинеарности наблюдается между факторами: Х1 – Х3, где rx1x3 > 0,8.
Задание 2. Постройте поле корреляции результативного признака и наиболее тесно связанного с ним фактора.
Задание 3 - 4. Рассчитайте параметры линейной парной регрессии для всех факторов X.
1. Линейная модель: y^ = a + b * x1.
Составим таблицу исходных и расчетных данных:
t
y
x1
x*x
y*x
у * у
(y - yср)2
(x1 - xср)2
y^
(y - y^)2
E, %
1
115
0
0
0
13225,0
455,8
0,3
117,5
6,3
2,2
2
85
1
1
85
7225,0
74,8
0,2
76,0
80,6
10,6
3
69
1
1
69
4761,0
607,6
0,2
76,0
49,3
10,2
4
57
1
1
57
3249,0
1343,2
0,2
76,0
361,7
33,4
5
184,6
0
0
0
34077,2
8271,9
0,3
117,5
4501,9
36,3
6
56
1
1
56
3136,0
1417,5
0,2
76,0
400,8
35,7
7
85
0
0
0
7225,0
74,8
0,3
117,5
1056,5
38,2
8
265
0
0
0
70225,0
29360,8
0,3
117,5
21755,2
55,7
9
60,65
1
1
60,65
3678,4
1089,0
0,2
76,0
236,2
25,3
10
130
0
0
0
16900,0
1321,3
0,3
117,5
156,2
9,6
11
46
1
1
46
2116,0
2270,5
0,2
76,0
901,2
65,3
12
115
0
0
0
13225,0
455,8
0,3
117,5
6,3
2,2
13
70,96
0
0
0
5035,3
514,8
0,3
117,5
2166,3
65,6
14
39,5
1
1
39,5
1560,3
2932,2
0,2
76,0
1333,7
92,5
15
78,9
0
0
0
6225,2
217,6
0,3
117,5
1490,2
48,9
16
60
1
1
60
3600,0
1132,3
0,2
76,0
256,6
26,7
17
100
1
1
100
10000,0
40,3
0,2
76,0
575,1
24,0
18
51
1
1
51
2601,0
1819,0
0,2
76,0
626,0
49,1
19
157
0
0
0
24649,0
4013,2
0,3
117,5
1560,0
25,2
20
123,5
1
1
123,5
15252,3
891,0
0,2
76,0
2254,4
38,4
21
55,2
0
0
0
3047,0
1478,4
0,3
117,5
3881,7
112,9
22
95,5
1
1
95,5
9120,3
3,4
0,2
76,0
379,5
20,4
23
57,6
0
0
0
3317,8
1299,6
0,3
117,5
3588,4
104,0
24
64,5
1
1
64,5
4160,3
849,7
0,2
76,0
132,7
17,9
25
92
1
1
92
8464,0
2,7
0,2
76,0
255,4
17,4
26
100
1
1
100
10000,0
40,3
0,2
76,0
575,1
24,0
27
81
0
0
0
6561,0
160,0
0,3
117,5
1332,5
45,1
28
65
1
1
65
4225,0
820,8
0,2
76,0
121,4
17,0
29
110
0
0
0
12100,0
267,3
0,3
117,5
56,3
6,8
30
42,1
1
1
42,1
1772,4
2657,4
0,2
76,0
1150,5
80,6
31
135
0
0
0
18225,0
1709,8
0,3
117,5
306,1
13,0
32
39,6
1
1
39,6
1568,2
2921,4
0,2
76,0
1326,4
92,0
33
57
1
1
57
3249,0
1343,2
0,2
76,0
361,7
33,4
34
80
0
0
0
6400,0
186,3
0,3
117,5
1406,5
46,9
35
61
1
1
61
3721,0
1066,0
0,2
76,0
225,6
24,6
36
69,6
1
1
69,6
4844,2
578,4
0,2
76,0
41,2
9,2
37
250
1
1
250
62500,0
24445,3
0,2
76,0
30269,2
69,6
38
64,5
1
1
64,5
4160,3
849,7
0,2
76,0
132,7
17,9
39
125
0
0
0
15625,0
982,8
0,3
117,5
56,2
6,0
40
152,3
0
0
0
23195,3
3439,8
0,3
117,5
1210,8
22,8
сумма
3746
23
23
1748
454221
103406,4
9,8
3746
86584
1476,2
ср.зн.
93,65
0,58
0,58
43,71
11355,53
2585,16
0,2
93,65
2164,61
36,9
Найдем параметры уравнения линейной регрессии:
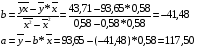
Итак, у^ = 117,50 + (-41,48)*Х1
Рассчитаем коэффицент детерминации:
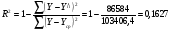
Оценим значимость уравнения регрессии с помощью F-критерия Фишера:
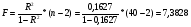
Fтабл = 4,40 (для a = 0,05; k1 = m = 1; k2 = n - m - 1 = 40 - 1 - 1 = 38)
Т.к. F > Fтабл, то с вероятностью 95% данное уравнение регрессии значимо
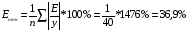Рассчитаем среднюю ошибку аппроксимации:
В среднем расчетные значения y* отличаются от фактических значений y на 36,9 %.
Линейная модель: y^ = a + b * x3.
Составим таблицу исходных и расчетных данных:
t
y
x3
x*x
y*x
у * у
(y - yср)2
(x - xср)2
y^
(y - y^)2
E, %
1
115
70,4
4956,16
8096
13225,0
455,8
1,3
95,5
380,6
17,0
2
85
82,8
6855,84
7038
7225,0
74,8
183,9
114,6
877,2
34,8
3
69
64,5
4160,25
4450,5
4761,0
607,6
22,5
86,4
302,4
25,2
4
57
55,1
3036,01
3140,7
3249,0
1343,2
199,9
71,9
221,7
26,1
5
184,6
83,9
7039,21
15487,94
34077,2
8271,9
214,9
116,3
4662,9
37,0
6
56
32,2
1036,84
1803,2
3136,0
1417,5
1372,0
36,6
377,8
34,7
7
85
65
4225
5525
7225,0
74,8
18,0
87,2
4,7
2,5
8
265
169,5
28730,25
44917,5
70225,0
29360,8
10052,1
248,4
276,9
6,3
9
60,65
74
5476
4488,1
3678,4
1089,0
22,7
101,0
1631,6
66,6
10
130
87
7569
11310
16900,0
1321,3
315,4
121,1
79,3
6,8
11
46
44
1936
2024
2116,0
2270,5
637,1
54,8
76,8
19,1
12
115
60
3600
6900
13225,0
455,8
85,4
79,4
1264,0
30,9
13
70,96
65,7
4316,49
4662,072
5035,3
514,8
12,5
88,2
298,6
24,4
14
39,5
42
1764
1659
1560,3
2932,2
742,0
51,7
148,4
30,8
15
78,9
49,3
2430,49
3889,77
6225,2
217,6
397,6
62,9
254,7
20,2
16
60
64,5
4160,25
3870
3600,0
1132,3
22,5
86,4
696,4
44,0
17
100
93,8
8798,44
9380
10000,0
40,3
603,2
131,6
997,7
31,6
18
51
64
4096
3264
2601,0
1819,0
27,5
85,6
1198,4
67,9
19
157
98
9604
15386
24649,0
4013,2
827,1
138,1
358,5
12,1
20
123,5
107,5
11556,25
13276,25
15252,3
891,0
1463,8
152,7
853,8
23,7
21
55,2
48
2304
2649,6
3047,0
1478,4
451,1
60,9
32,9
10,4
22
95,5
80
6400
7640
9120,3
3,4
115,8
110,3
219,0
15,5
23
57,6
63,9
4083,21
3680,64
3317,8
1299,6
28,5
85,5
776,3
48,4
24
64,5
58,1
3375,61
3747,45
4160,3
849,7
124,1
76,5
144,4
18,6
25
92
83
6889
7636
8464,0
2,7
189,3
114,9
525,6
24,9
26
100
73,4
5387,56
7340
10000,0
40,3
17,3
100,1
0,0
0,1
27
81
45,5
2070,25
3685,5
6561,0
160,0
563,6
57,1
572,2
29,5
28
65
32
1024
2080
4225,0
820,8
1386,8
36,3
826,3
44,2
29
110
65,2
4251,04
7172
12100,0
267,3
16,3
87,5
507,7
20,5
30
42,1
40,3
1624,09
1696,63
1772,4
2657,4
837,5
49,1
48,4
16,5
31
135
72
5184
9720
18225,0
1709,8
7,6
98,0
1372,1
27,4
32
39,6
36
1296
1425,6
1568,2
2921,4
1104,9
42,4
8,0
7,1
33
57
61,6
3794,56
3511,2
3249,0
1343,2
58,4
81,9
620,8
43,7
34
80
35,5
1260,25
2840
6400,0
186,3
1138,4
41,7
1470,5
47,9
35
61
58,1
3375,61
3544,1
3721,0
1066,0
124,1
76,5
240,7
25,4
36
69,6
83
6889
5776,8
4844,2
578,4
189,3
114,9
2054,5
65,1
37
250
152
23104
38000
62500,0
24445,3
6849,2
221,4
819,9
11,5
38
64,5
64,5
4160,25
4160,25
4160,3
849,7
22,5
86,4
479,1
33,9
39
125
54
2916
6750
15625,0
982,8
232,3
70,2
3004,0
43,8
40
152,3
89
7921
13554,7
23195,3
3439,8
390,5
124,2
790,6
18,5
сумма
3746
2768
222656
307179
454221
103406
31068,8
3746
29475
1114,8
ср.зн.
93,65
69,21
5566,40
7679,46
11355,53
2585,16
776,72
93,65
736,88
27,9
Найдем параметры уравнения линейной регрессии:
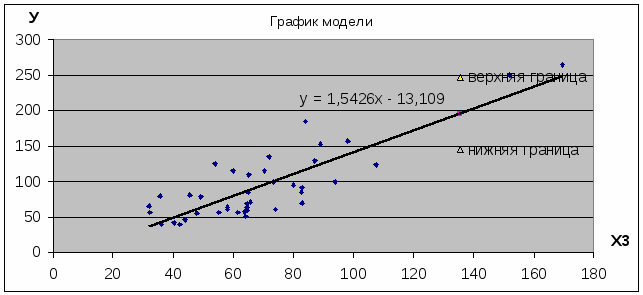
Итак: у^ = -13.11 + 1.54 * х3
Рассчитаем коэффицент детерминации:
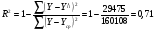
Можно сказать, что вариация признака Y на 90,3% объясняется вариацией признака X3.
Оценим значимость уравнения регрессии с помощью F - критерия Фишера:
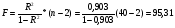
Fтабл = 4,40 (для a = 0,05; k1 = m = 1; k2 = n - m - 1 = 40 - 1 - 1 = 38).
Т.к. F > Fтабл, то с вероятностью 95% данное уравнение регрессии значимо.
Рассчитаем среднюю ошибку аппроксимации:
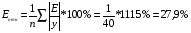
В среднем расчетные значения y* отличаются от фактических значений y на 27,9 %.
3. Линейная модель: y^ = a + b * x5
Составим таблицу исходных и расчетных данных:
t
y
x5
x*x
y*x
у * у
(y – yср)2
(x – xср)2
y^
(y - y^)2
E, %
1
115
9
81
1035
13225,0
455,8
3,8
97,3
312,2
15,4
2
85
5
25
425
7225,0
74,8
4,2
89,8
22,9
5,6
3
69
6
36
414
4761,0
607,6
1,1
91,7
513,9
32,9
4
57
1
1
57
3249,0
1343,2
36,6
82,2
636,6
44,3
5
184,6
1
1
184,6
34077,2
8271,9
36,6
82,2
10479,5
55,5
6
56
2
4
112
3136,0
1417,5
25,5
84,1
790,6
50,2
7
85
12
144
1020
7225,0
74,8
24,5
103,0
323,8
21,2
8
265
10
100
2650
70225,0
29360,8
8,7
99,2
27483,5
62,6
9
60,65
11
121
667,15
3678,4
1089,0
15,6
101,1
1636,7
66,7
10
130
6
36
780
16900,0
1321,3
1,1
91,7
1469,3
29,5
11
46
2
4
92
2116,0
2270,5
25,5
84,1
1453,0
82,9
12
115
2
4
230
13225,0
455,8
25,5
84,1
953,7
26,9
13
70,96
5
25
354,8
5035,3
514,8
4,2
89,8
354,2
26,5
14
39,5
7
49
276,5
1560,3
2932,2
0,0
93,6
2922,0
136,9
15
78,9
14
196
1104,6
6225,2
217,6
48,3
106,8
776,7
35,3
16
60
11
121
660
3600,0
1132,3
15,6
101,1
1689,7
68,5
17
100
1
1
100
10000,0
40,3
36,6
82,2
315,8
17,8
18
51
6
36
306
2601,0
1819,0
1,1
91,7
1653,9
79,7
19
157
2
4
314
24649,0
4013,2
25,5
84,1
5311,8
46,4
20
123,5
12
144
1482
15252,3
891,0
24,5
103,0
420,5
16,6
21
55,2
9
81
496,8
3047,0
1478,4
3,8
97,3
1775,0
76,3
22
95,5
6
36
573
9120,3
3,4
1,1
91,7
14,7
4,0
23
57,6
5
25
288
3317,8
1299,6
4,2
89,8
1035,6
55,9
24
64,5
10
100
645
4160,3
849,7
8,7
99,2
1205,4
53,8
25
92
9
81
828
8464,0
2,7
3,8
97,3
28,4
5,8
26
100
2
4
200
10000,0
40,3
25,5
84,1
252,2
15,9
27
81
3
9
243
6561,0
160,0
16,4
86,0
25,1
6,2
28
65
5
25
325
4225,0
820,8
4,2
89,8
614,1
38,1
29
110
10
100
1100
12100,0
267,3
8,7
99,2
116,2
9,8
30
42,1
13
169
547,3
1772,4
2657,4
35,4
104,9
3941,5
149,1
31
135
12
144
1620
18225,0
1709,8
24,5
103,0
1024,4
23,7
32
39,6
5
25
198
1568,2
2921,4
4,2
89,8
2518,1
126,7
33
57
8
64
456
3249,0
1343,2
0,9
95,4
1477,9
67,4
34
80
4
16
320
6400,0
186,3
9,3
87,9
62,3
9,9
35
61
10
100
610
3721,0
1066,0
8,7
99,2
1460,7
62,7
36
69,6
4
16
278,4
4844,2
578,4
9,3
87,9
334,6
26,3
37
250
15
225
3750
62500,0
24445,3
63,2
108,7
19978,0
56,5
38
64,5
12
144
774
4160,3
849,7
24,5
103,0
1481,8
59,7
39
125
8
64
1000
15625,0
982,8
0,9
95,4
873,6
23,6
40
152,3
7
49
1066,1
23195,3
3439,8
0,0
93,6
3450,9
38,6
сумма
3746
282
2610
27583
454221
103406
75597,5
3746
101191
1831,2
ср.зн.
93,65
7,05
65,25
689,58
11355,53
2585,16
1889,94
93,65
2529,77
45,8
Найдем параметры уравнения линейной регрессии:
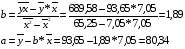
Итак, у^ = 80,34 + 1,89 * х5.
Расcчитаем коэффициент детерминации:
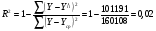
Можно сказать, что вариация признака Y на 60,7% объясняется вариацией признака X5.
Оценим значимость уравнения регрессии с помощью F-критерия Фишера:
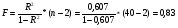
Fтабл = 4,40 (для a = 0,05; k1 = m = 1; k2 = n - m - 1 = 40 - 1 - 1 = 38).
Т.к. F > Fтабл, то с вероятностью 95% данное уравнение регрессии значимо
Рассчитаем среднюю ошибку аппроксимации:
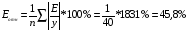
В среднем расчетные значения y* отличаются от фактических значений y на 45,8 %.
Сравним модели:
R
F
Eотн
модель 1
0,16
7,38
36,9%
модель 2
0,71
95,31
27,9%
модель 3
0,02
0,83
45,8%
- лучшая модель – модель2
Задание 5. Осуществите прогнозирование для лучшей модели среднего значения показателя У при уровне значимости а = 0.1, если прогнозное значение фактора Х составит 80% от его максимального значения. Представьте графически: фактические и модельные значения, точки прогноза.
Пусть прогнозное значение Х составляет 80% относительно максимального значения (Хmах):
Хпр = Хmax * 80% / 100% = 169.5 * 0,8 = 135.6
Упр = -13,11 + 1,54 * 135,6 = 196,07
Границы доверительного интервала прогноза:
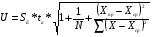
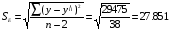
tа = 1,68 (для a = 0,10; k = n - m - 1 = 40 - 1 - 1 = 38).
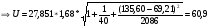
Интервальный прогноз:
Верхняя граница прогноза Ув = Упр + U = 196,07 + 50,543 = 246,613
145,527 < Упр < 246,613
6. Используя пошаговую множественную регрессию (метод исключения или метод включения), постройте модель формирования цены квартиры за счет значимых факторов. Дайте экономическую интерпретацию коэффициентов модели регрессии.
Построим модель зависимости стоимости кватриры от всех факторов.
Используя функцию "Регрессия" в арсенале M.Excel, рассчитаем характеристики модели автоматически:
см. ПРИЛОЖЕНИЕ 1
Модель имеет вид:
У = 12,606 + (- 34,44) * Х1 + 1,5087 * Х3 + (- 0,506) * Х5
R2 = 0,829, F = 57,99
Fтабл = 3,20 (для a = 0,05; k1 = m = 3; k2 = n - m - 1 = 40 - 3 - 1 = 36)
Т.к. F > Fтабл, то с вероятностью 95% данное уравнение регрессии значимо.
Оценим значимость параметров уравнения регрессии с помощью t - критерия Стьюдента:
tyx1 =
-4,83
tyx3 =
11,62
tyx5 =
-0,55
> 2,03 → коэф-т корреляции между факторами у и х1 значим
> 2,03 → коэф-т корреляции между факторами у и х3 значим
< 2,03 → коэф-т корреляции между факторами у и х5 незначим
Исключим фактор Х5 как незначимый.
Используя функцию "Регрессия" в арсенале M.Excel, рассчитаем характеристики модели автоматически:
см. ПРИЛОЖЕНИЕ 2
Модель имеет вид:
У = 10,255 + (- 34,56) * Х1 + 1,492 * Х3
R2 = 0,827, F = 88,49
Fтабл = 3,20 (для a = 0,05; k1 = m = 3; k2 = n - m - 1 = 40 - 2 - 1 = 37)
Т.к. F > Fтабл, то с вероятностью 95% данное уравнение регрессии значимо
Оценим значимость параметров уравнения регрессии с помощью t - критерия Стьюдента:
tyx1 =
-4,90
tyx3 =
11,92
> 2,03 → коэф-т корреляции между факторами у и х1 значим
> 2,03 → коэф-т корреляции между факторами у и х3 значим
Т.к. все параметры значимы, то мы получили модель формирования цены квартиры за счет значимых факторов.
Задание 7. Оцените качество построенной модели. Улучшилось ли качество модели по сравнению с однофакторной моделью? Дайте оценку влияния значимых факторов на результат с помощью коэффициентов эластичности, β- и ∆-коэффициентов.
Итак, для анализа используем модель:
У =10,255 + (- 34,44) * Х1 + 1,4921 * Х3
Значение "b1" = - 34,44 означает, что с ростом фактора Х1 на 1 единицу (смена города), цена квартиры снизится на -34,44 тыс.долл.
Значение "b2" = 1,49 означает, что с ростом фактора Х3 на 1 единицу (1 кв.м.), цена квартиры вырастет на 1,49 тыс. долл.
R2 = 0,827 - это значение выше, чем значение R2 однофакторной модели
F =88,49
Fтабл = 3,20 (для a = 0,05; k1 = m = 3; k2 = n - m - 1 = 40 - 2 - 1 = 37).
Т.к. F > Fтабл, то с вероятностью 95% данное уравнение регрессии значимо.
Рассчитаем ряд коэффицентов:
Результаты регрессионного анализа
Множественный R
0,9094
R-квадрат
0,8271
Нормированный R-квадрат
0,8177
Стандартная ошибка
21,9831
Коэффициенты регрессии
ryxj
Хср
Sx
Y-пересечение
10,25
1
93,7
50,8
Х1
-34,56
-0,403
0,6
0,5
Х3
1,49
0,846
69,2
27,9
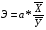
1) коэффициент эластичности:
Э1 = -34,56 * 0,6 / 93,7 = - 0,21(c ростом Х1 на 1% снижение У составит - 0,21%)
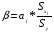Э2 = 1,49 * 69,2 / 93,7 = 1,10 (c ростом Х3 на 1% рост У составит 1,10%)
2) β - коэффициент:
β1 = -34,56 * 0,5 / 50,8 = -0,34
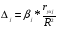β2 = 1,49 * 27,9 / 50,8 = 0,82
3) ∆ - коэффициент:
∆1 = - 0,336 *(-0,403) / 0,827 = 0,16 фактор Х1 оказывает 16% всего влияния
∆2 = 0,818 * 0,846 / 0,827 = 0,84 фактор Х3 оказывает 84% всего влияния
ЗАДАЧА 2. Исследовать динамику экономического показателя на основе анализа одномерного временного ряда.
В течение девяти последовательных недель фиксировался спрос Y(t) (млн. руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя :
№НАБЛЮДЕНИЯ
1
2
3
4
5
6
7
8
9
10
14
21
24
33
41
44
47
49
Проверить наличие аномальных наблюдений.
Построить линейную модель Y^(t) = a0 + a1 t, параметры которой оценить МНК (Y^(t)) – расчетные, смоделированные значения временного ряда.
Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S-критерия взять табулированные границы 2,7 – 3,7).
Оценить точность моделей на основе использования средней относительной ошибки аппроксимации.
Осуществить прогноз спроса на следующие 2 недели (доверительный интервал прогноза рассчитать при доверительной вероятности р = 90%).
Фактические значения показателя, результаты моделирования представить графически.
Проверить наличие аномальных наблюдений:
t
Y(t)
для метода Ирвина
Z(t) =
h(t) =
h(t)2
Q(t) = Z(t) / S
Вывод
Y(t) - Y(t-1)
Y(t) - Ycp
1
10
-21,44
459,86
2
14
4
-17,44
304,31
0,27
= 4 / 14,71
< 1,52, т.е. точка не аномальна
3
21
7
-10,44
109,09
0,48
= 7 / 14,71
< 1,52, т.е. точка не аномальна
4
24
3
-7,44
55,42
0,20
= 3 / 14,71
< 1,52, т.е. точка не аномальна
5
33
9
1,56
2,42
0,61
= 9 / 14,71
< 1,52, т.е. точка не аномальна
6
41
8
9,56
91,31
0,54
= 8 / 14,71
< 1,52, т.е. точка не аномальна
7
44
3
12,56
157,64
0,20
= 3 / 14,71
< 1,52, т.е. точка не аномальна
8
47
3
15,56
241,98
0,20
= 3 / 14,71
< 1,52, т.е. точка не аномальна
9
49
2
17,56
308,20
0,14
= 2 / 14,71
< 1,52, т.е. точка не аномальна
283
1730,22
1. Наличие аномальных точек определим по методу Ирвина, для чего определим значения Q(t): Q(t) = Z(t) / S
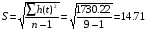
Сравним полученные значения Q(t) с критическим значением Qкрит = 1,52
если Q(t) > Qкрит, то точка аномальна
если Q(t) < Qкрит, то точка не аномальна
Вывод: аномальных точек нет
Проведем анализ самого ряда:
(t-tcp) * (Y-Ycp)
E(t) =
R(t) =
R(t)2
E(t)*E(t-1)
[E(t)/Y(t)] * 100
t
Y(t)
t-tcp
(t-tcp)2
Y-Ycp
Yл(t)
Y(t)-Yл(t)
E(t)2
P
E(t)-E(t-1)
1
10
-4
16
-21,44
85,8
10,2
-0,2
0,06
2,444
2
14
-3
9
-17,44
52,3
15,5
-1,5
2,39
1
-1,30
1,69
0,38
11,032
3
21
-2
4
-10,44
20,9
20,8
0,2
0,02
1
1,70
2,89
-0,24
0,741
4
24
-1
1
-7,44
7,4
26,1
-2,1
4,60
1
-2,30
5,29
-0,33
8,935
5
33
0
0
1,56
0,0
31,4
1,6
2,42
0
3,70
13,69
-3,34
4,714
6
41
1
1
9,56
9,6
36,7
4,3
18,11
1
2,70
7,29
6,62
10,379
7
44
2
4
12,56
25,1
42,0
2,0
3,82
0
-2,30
5,29
8,32
4,444
8
47
3
9
15,56
46,7
47,3
-0,3
0,12
0
-2,30
5,29
-0,67
0,733
9
49
4
16
17,56
70,2
52,6
-3,6
13,28
-3,30
10,89
1,26
7,438
10
57,9
11
63,2
45
283
0
60
318
283,0
44,82
4
-3,40
52,32
11,9914
50,8603
2. Рассчитаем по методу наименьших квадратов параметры "a" и "b" линейной модели : Y* = a + b * t
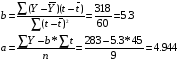
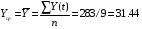
Где
Итак, Y* = 4,944 + 5,3 * t.
Оценим адекватность полученной модели:
а) случайность уровней ряда E(t) проверим по критерию поворотных точек Р:
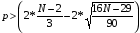
Р > 2, у нас р = 4
т.к. Р > 2, то свойство случайности выполняется.
б) независимость (отсутствие автокорреляции) уровней ряда E(t) проверим по критерию Дарбина-Уотсона:
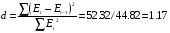
d(1) = 1,08
d(1) = 1.36
T.к. d находится в интервале (d(1); d(2)), то критерий Дарбина-Уотсона не используется.
Рассчитаем первый коэффициент корреляции:
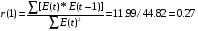
Т.к. по модулю r(1) < 0,36, то свойство независимости выполняется.
в) соответствие нормальному закону распределения (НЗР) проверим по RS-критерию:
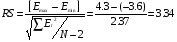
т.к.RS = 3,34 принадлежит интервалу [RSmin ; RSmax] (RSmin=2,7; RSmax=3,7 из таблицы), то гипотеза о НЗР уровней ряда E(t) подтверждается, что позволяет сделать прогноз.
5. Оценим точность модели по средней относительной ошибке аппроксимации:
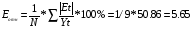
Т.к. Еотн = 5,65 < 15%, то модель признается допустимой по точности.
6. Прогноз:
при k=1: t =9+1=10
при k=2: t =9+2=11
k- шаг прогноза
Y*(10) = 4,944 + 5,3 * 10 = 57,94
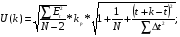Y*(11) = 4,944 + 5,3 * 11 = 63,24
Границы доверительного интервала прогноза:
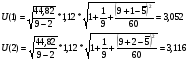
при k=1
при k=2
Y10 = Y*(10) +/-U(1) = 57.94 +/- 3.28
Y11 = Y*(11) +/- U(2) = 63.24 +/- 3.48
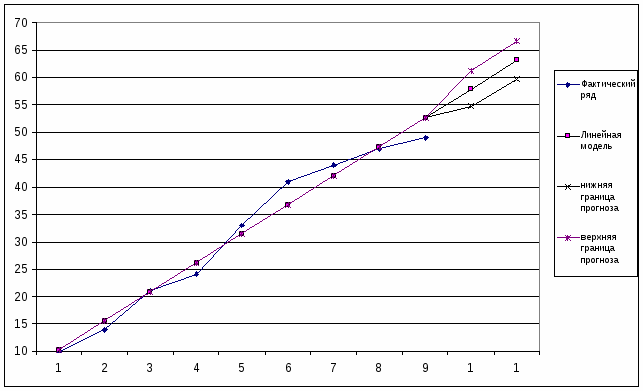
Таблица прогнозных значений:
Точечный прогноз
Нижняя граница прогноза
Верхняя граница прогноза
к = 1
57,94
54,66
61,23
к = 2
63,24
59,77
66,72
7. Представим на графике фактические данные, результаты моделирования и прогнозирования:
Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ