по курсу эконометрика
вариант
Задача 1
Администрация страховой компании приняла решение о введении нового вида услуг – страхование на случай пожара. С целью определения тарифов по выборке из 10 случаев пожаров анализируется зависимость стоимости ущерба, нанесенного пожаром от расстояния до ближайшей пожарной станции:
№ п/п
Общая сумма ущерба, млн.руб.
26,2
17,8
31,3
23,1
27,5
36,0
14,1
22,3
19,6
31,3
Расстояние до ближайшей станции, км
3,4
1,8
4,6
2,3
3,1
5,5
0,7
3,0
2,6
4,3
Построить поле корреляции результата и фактора
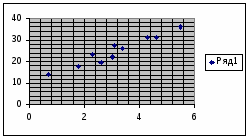
Поле корреляции результата (общая сумма ущерба) и фактора (расстояние до ближайшей пожарной станции).
На основании поля корреляции можно сделать вывод , что между факторным (Х) и результативным (Y) признаками существует прямая зависимость.
Определить параметры а и b уравнения парной линейной регрессии:
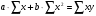
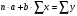

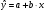

где n число наблюдений в совокупности ( в нашем случае 10)
a и b искомые параметры
x и y фактические значения факторного и результативного признаков.
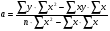
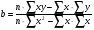
Для определения сумм составим расчетную таблицу из пяти граф, в графе 6 дадим выравненное значение y (ŷ).
В графах 7,8,9 рассчитаем суммы, которые использованы в формулах пунктов 4,5 данной задачи.
-
№
X
Y
X²
x·y
y²
ŷ
(y-ŷ)
(x-x)
(ŷ-y)²
1
2
3
4
5
6
7
8
9
3,4
26,2
11,56
686,44
89,08
26,20
0,00
0,0729
1,6384
1,8
17,8
3,24
316,84
32,04
18,70
0,81
1,7689
36,6884
4,6
31,3
21,16
979,69
143,98
31,80
0,25
2,1609
47,3344
2,3
23,1
5,29
533,61
53,13
21,00
4,41
0,6889
15,3664
3,1
27,5
9,61
756,25
85,25
7,29
0,0009
0,0144
5,5
36
30,25
1296
198
36,00
0,00
5,6169
122,7664
0,7
14,1
0,49
198,81
9,87
13,50
0,36
5,9049
130,4164
3
22,3
9
497,29
66,9
24,30
4,00
0,0169
0,3844
2,6
19,6
6,76
384,16
50,96
22,40
7,84
0,2809
6,3504
4,3
31,3
18,49
979,69
134,59
30,40
0,81
1,3689
30,0304
∑
31,3
249,2
115,85
6628,78
863,8
249,1
25,77
17,881
390,9900
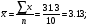
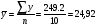
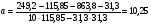
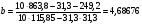
Коэффициент регрессии (b) показывает абсолютную силу связи между вариацией x и вариацией y. Применительно к данной задаче можно сказать, что при применении расстояния до ближайшей пожарной станции на 1 км общая сумма ущерба изменяется в среднем на 4,686 млн.руб.
Таким образом, управление регрессии имеет следующий вид:
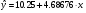 Линейный коэффициент корреляции определяется по формуле:
Линейный коэффициент корреляции определяется по формуле:
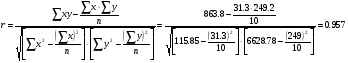
В соответствии со шкалой Чеддока можно говорить о высокой тесноте связи между y и x, r = 0.957.
Квадрат коэффициента корреляции называется коэффициентом детерминации
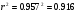 Это означает, что доля вариации y объясненная вариацией фактора x включенного в уравнение регрессии равна 91,6%, а остальные 8,4% вариации приходятся на долю других факторов, не учтенных в уравнении регрессии
Это означает, что доля вариации y объясненная вариацией фактора x включенного в уравнение регрессии равна 91,6%, а остальные 8,4% вариации приходятся на долю других факторов, не учтенных в уравнении регрессии
Статистическую значимость коэффициента регрессии «b» проверяем с помощью t-критерия Стьюдента. Для этого сначала определяем остаточную сумму квадратов:
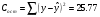 и ее среднее квадратическое отклонение:
и ее среднее квадратическое отклонение:
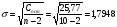
Найдем стандартную ошибку коэффициента регрессии по формуле:
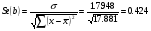
Фактическое значение t-критерия Стьюдента для коэффициента регрессии «b» рассчитывается как
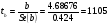 Полученное фактическое значение tb сравнивается с критическим tk , который получается по талблице Стьюдента с учетом принятого уровня значимости L=0,05 (для вероятности 0,95) и числа степеней свободы
Полученное фактическое значение tb сравнивается с критическим tk , который получается по талблице Стьюдента с учетом принятого уровня значимости L=0,05 (для вероятности 0,95) и числа степеней свободы
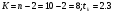 Полученный коэффициент регрессии признается типичным, т.к.
Полученный коэффициент регрессии признается типичным, т.к.
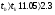 Оценка статистической значимости построенной модели регрессии в целом производится с помощью F-критерия Фишера
Оценка статистической значимости построенной модели регрессии в целом производится с помощью F-критерия Фишера
Фактическое значение критерия для уравнения определяется как
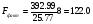
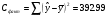
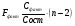 Fфакт сравнивается с критическим значением Fк, которое определяется по таблице F-критерия с учетом принятого уровня значимости L=0,05 (для вероятности 0,95) и числа степеней свободы:
Fфакт сравнивается с критическим значением Fк, которое определяется по таблице F-критерия с учетом принятого уровня значимости L=0,05 (для вероятности 0,95) и числа степеней свободы:
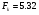
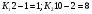
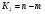
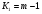
Следовательно, при Fфакт>Fк уравнении регрессии в целом признается существенным.
По исходным данным полагают, что расстояние до ближайшей пожарной станции
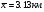 уменьшится на 5% от своего среднего уровня
уменьшится на 5% от своего среднего уровня
Следовательно, значения факторного признака для точечного прогноза:
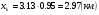 а точечный прогноз :
а точечный прогноз :
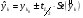
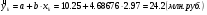 Строим доверительный интервал прогноза ущерба с вероятностью 0,95 (L=0,05) по формуле
Строим доверительный интервал прогноза ущерба с вероятностью 0,95 (L=0,05) по формуле
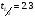
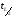 Табличное значение t-критерия Стьюдента для уровня значимости L=0,05 и числа степеней свободы п-2=10-2=8,
Табличное значение t-критерия Стьюдента для уровня значимости L=0,05 и числа степеней свободы п-2=10-2=8,
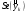 Стандартная ошибка точечного прогноза рассчитываемая по формуле
Стандартная ошибка точечного прогноза рассчитываемая по формуле
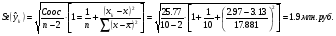 Отсюда доверительный интервал составляет:
Отсюда доверительный интервал составляет:
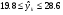
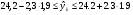
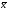
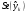 Из полученных результатов видно, что интервал от 19,8 до 28,6 млн. руб. ожидаемой величины ущерба довольно широкий. Значительная неопределенность прогноза линии регрессии, это видно из формулы связана прежде всего с малым объемом выборки (n=10), а также тем, что по мере удаления xk от ширина доверительного интервала увеличивается.
Из полученных результатов видно, что интервал от 19,8 до 28,6 млн. руб. ожидаемой величины ущерба довольно широкий. Значительная неопределенность прогноза линии регрессии, это видно из формулы связана прежде всего с малым объемом выборки (n=10), а также тем, что по мере удаления xk от ширина доверительного интервала увеличивается.
Задача 2
Имеются следующие данные о ценах и дивидендах по обыкновенным акциям, также о доходности компании.
№
цена акции лоллар США
доходность капитала %
уровень дивидендов %
1
25
15,2
2,6
2
20
13,9
2,1
3
15
15,8
1,5
4
34
12,8
3,1
5
20
6,9
2,5
6
33
14,6
3,1
7
28
15,4
2,9
8
30
17,3
2,8
9
23
13,7
2,4
10
24
12,7
2,4
11
25
15,3
2,6
12
26
15,2
2,8
13
26
12
2,7
14
20
15,3
1,9
15
20
13,7
1,9
16
13
13,3
1,6
17
21
15,1
2,4
18
31
15
3
19
26
11,2
3,1
20
11
12,1
2
построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров
Составим расчетную таблицу
№
y
X1
X2
X2*X2
X1*X1
y*X1
y*x2
X1*X2
1
25
15,2
2,6
6,76
231,04
380
65
39,52
2
20
13,9
2,1
4,41
193,21
278
42
29,19
3
15
15,8
1,5
2,25
249,64
237
22,5
23,7
4
34
12,8
3,1
9,61
163,84
435,2
105,4
39,68
5
20
6,9
2,5
6,25
47,61
138
50
17,25
6
33
14,6
3,1
9,61
213,16
481,8
102,3
45,26
7
28
15,4
2,9
8,41
237,16
431,2
81,2
44,66
8
30
17,3
2,8
7,84
299,29
519
84
48,44
9
23
13,7
2,4
5,76
187,69
315,1
55,2
32,88
10
24
12,7
2,4
5,76
161,29
304,8
57,6
30,48
11
25
15,3
2,6
6,76
234,09
382,5
65
39,78
12
26
15,2
2,8
7,84
231,04
395,2
72,8
42,56
13
26
12
2,7
7,29
144
312
70,2
32,4
14
20
15,3
1,9
3,61
234,09
306
38
29,07
15
20
13,7
1,9
3,61
187,69
274
38
26,03
16
13
13,3
1,6
2,56
176,89
172,9
20,8
21,28
17
21
15,1
2,4
5,76
228,01
317,1
50,4
36,24
18
31
15
3
9
225
465
93
45
19
26
11,2
3,1
9,61
125,44
291,2
80,6
34,72
20
11
12,1
2
4
146,41
133,1
22
24,2
итого
471
276,5
49,4
126,7
3916,59
6569,1
1216
682,34
Опрелеляем
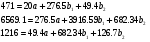
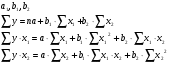
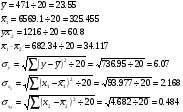 По Данным таблицы составим систему нормальных уравнений с тремя неизвестными:
По Данным таблицы составим систему нормальных уравнений с тремя неизвестными:
Разделим каждое уравнение на коэффициент при a.
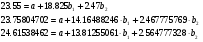 Вычтем первое уравнение из второго и третьего
Вычтем первое уравнение из второго и третьего
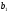
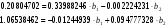
 Разделим каждое уравнение на коэффициент при
Разделим каждое уравнение на коэффициент при
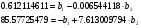

Сложим оба уравнения и найдем
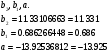
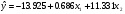 Таким образом, уравнение множественной регрессии имеет вид
Таким образом, уравнение множественной регрессии имеет вид
Экономический смысл коэффициентов 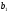 и
и 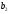 в том, что это показатели силы связи, характеризующие изменение цены акции при изменении какого-либо факторного признака на единицу своего измерения при фиксированном влиянии другого фактора. Так, при изменении доходности капитала на один процентный пункт, цена акции измениться в том же направлении на 0,686 долларов; при изменении уровня дивидендов на один процентный пункт цена акции изменится в том же направлении на 11,331 доллара.
в том, что это показатели силы связи, характеризующие изменение цены акции при изменении какого-либо факторного признака на единицу своего измерения при фиксированном влиянии другого фактора. Так, при изменении доходности капитала на один процентный пункт, цена акции измениться в том же направлении на 0,686 долларов; при изменении уровня дивидендов на один процентный пункт цена акции изменится в том же направлении на 11,331 доллара.
Рассчитать частные коэффициенты эластичности.
Будем рассчитывать частные коэффициенты эластичности для среднего значения фактора и результата:
Э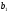 - эластичность цены акции по доходности капитала
- эластичность цены акции по доходности капитала
Э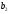 - эластичность цены акции по уровню дивидендов
- эластичность цены акции по уровню дивидендов
 Определить стандартизованные коэффициенты регрессии
Определить стандартизованные коэффициенты регрессии
формулы определения:
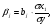 где j- порядковый номер фактора
где j- порядковый номер фактора
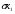 - среднее квадратическое отклонение j-го фактора (вычислено раньше)
- среднее квадратическое отклонение j-го фактора (вычислено раньше)
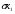 =2,168
=2,168 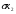 = ,0484
= ,0484
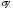 - среднее квадратическое отклонение результативного признака
- среднее квадратическое отклонение результативного признака
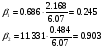
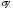 =6,07
=6,07
сделать вывод о силе связи результата с каждым из факторов.
Коэффициенты эластичности факторов 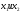 говорят о том, что при отклонении величины соответствующего фактора от его средней величины на 1% (% как относительная величина) и при отвлечении от сопутствующего отклонения другого фактора входящего в уравнение множественной регрессии, цена акции отклонится от своего среднего значения на 0,403% при действии фактора
говорят о том, что при отклонении величины соответствующего фактора от его средней величины на 1% (% как относительная величина) и при отвлечении от сопутствующего отклонения другого фактора входящего в уравнение множественной регрессии, цена акции отклонится от своего среднего значения на 0,403% при действии фактора 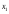 (доходность капитала) и на 1,188% при действии фактора
(доходность капитала) и на 1,188% при действии фактора 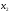 (уровень дивидендов).
(уровень дивидендов).
Таким образом сила влияния фактора 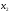 на результат (цену акции) больше, чем фактора
на результат (цену акции) больше, чем фактора 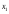 , а сами факторы действуют в одном и том же положительном направлениии.
, а сами факторы действуют в одном и том же положительном направлениии.
Количественно фактор 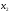 приблизительно в три раза сильнее влияет на результат чем фактор
приблизительно в три раза сильнее влияет на результат чем фактор 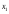 . (
. (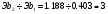 )
)
Анализ уравнения регрессии по стандартизованным коэффициентам 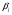 показывает, что второй фактор влияет сильнее на результат, чем фактор
показывает, что второй фактор влияет сильнее на результат, чем фактор 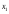 (
(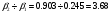 ), т.е. при учете вариации факторов их влияние более точно.
), т.е. при учете вариации факторов их влияние более точно.
Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции.
Парные коэффициенты корреляции определяются по формулам:
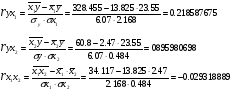
Частные коэффициенты корреляции определяются по ф-ле:
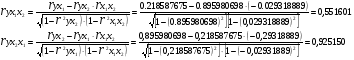 Множественный коэффициент корреляции определяется по формуле:
Множественный коэффициент корреляции определяется по формуле:
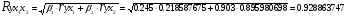
Матрица парных коэффициентов корреляции
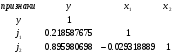
Из таблицы видно, что в соответствии со шкалой Чеддока связь между 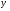 и
и 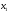 можно оценить как слабую, между
можно оценить как слабую, между 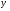 и
и 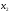 - как высокую, между
- как высокую, между 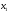 и
и 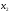 связь практически отсутствует.
связь практически отсутствует.
Таким образом, по построенной модели можно сделать вывод об отсутствии в ней мультиколлениарности факторов.
Частные коэффициенты корреляции рассчитывались как оценки вклада во множественной коэффициент корреляции каждого из факторов (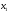 и
и 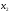 ). Они характеризуют связи между результативными признаками (ценой акции) и соответствующим фактором x при
). Они характеризуют связи между результативными признаками (ценой акции) и соответствующим фактором x при
Причина различий между значениями частных и парных коэффициентов корреляции состоит в том, что частный коэффициент отражает долю вариации результативного прихнака (цены акции), дополнительно объясняемой при включении фактора 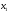 (или
(или 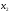 ) после другого фактора
) после другого фактора 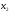 (или
(или 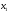 ) в уравнение регрессии, не объяснимой ранее включенным фактором
) в уравнение регрессии, не объяснимой ранее включенным фактором 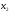 (или
(или 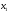 ).
).
6.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ