Поиск кратчайших сетей


 Поиск кратчайших сетей
Поиск кратчайших сетей
Маршалл У. Берн, Рональд Л. Грэм
Как найти кратчайшую сеть отрезков прямых линий, соединяющих произвольное множество, скажем из 100, точек? Эта задача не поддаётся ни самым быстродействующим компьютерам, ни самым изобретательным математическим умам
Представим себе такую ситуацию: некая телефонная компании Steiner Telephone Company подсчитала, что можно сэкономить несколько миллионов долларов, если удастся найти кратчайшую из возможных сетей телефонных линий, соединяющих 100 населённых пунктов. Чтобы решить эту задачу, компания заключила контракт с компьютерной компанией Cavalieri Computer Company, располагающей самыми быстродействующими в мире компьютерами и самыми квалифицированными программистами. Через неделю Cavalieri продемонстрировала в действии программу для решения поставленной задачи. Программа действительно нашла кратчайшую сеть для 15 абонентов всего за один час. Steiner заплатила 1000 долл. за программу и пообещала платить по одному центу за каждую секунду машинного времени, которое потребуется компьютеру для полного решения задачи. К тому времени, когда компьютер завершил вычисления для всех 100 абонентов, телефонная компания задолжала компьютерной многие триллионы долларов, а сами абоненты переместились на много километров со своих мест — либо по своему желанию, либо по причине континентального дрейфа!
Может быть, Cavalieri продала Steiner неправильную программу? Попробуем разобраться. Здесь мы столкнулись с одним из примеров так называемой задачи Штейнера, в которой требуется найти кратчайшую сеть прямолинейных отрезков, связывающих между собой заданное множество точек.
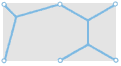
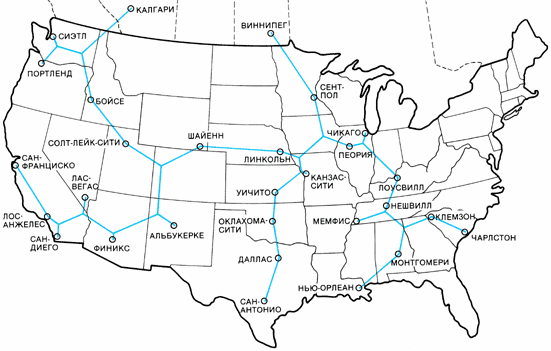
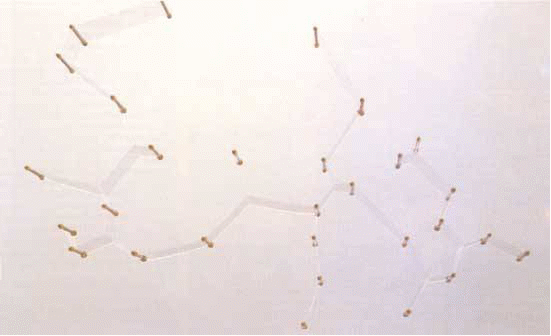
Компьютер из мыльной плёнки (вверху) соревнуется с электронным компьютером (внизу), отыскивая кратчайшую сеть, связывающую между собой 29 городов. Компьютер из мыльной плёнки, в котором расположение штырьков моделирует географию городов, минимизирует длину плёночных соединений в локальной области. Он даёт короткую сеть, но необязательно кратчайшую. Электронный компьютер реализует алгоритм Э. Кокейна и Д. Хьюджилла из Университета Виктории. Алгоритм гарантирует кратчайшую сеть. Задача с 29 точками на сегодня близка к пределу вычислительных возможностей.
Задачу Штейнера невозможно решить, просто рисуя линии между заданными точками. Для решения необходимо добавить новые точки, называемые точками Штейнера и служащие в качестве узлов искомой кратчайшей сети. Чтобы определить количество и расположение точек Штейнера, математики и программисты разработали специальные алгоритмы. Однако даже лучшие из этих алгоритмов, выполняющиеся на самых быстродействующих компьютерах, не в состоянии дать решение для большого множества заданных точек за реально приемлемое время. Более того, задача Штейнера принадлежит к классу задач, для которых, по мнению многих современных исследователей, эффективные алгоритмы, по-видимому, так никогда и не будут найдены. Поэтому компьютерная компания Cavalieri должна быть реабилитирована.
В то же время фирма Cavalieri могла бы разработать практически полезную программу, которая находила бы сеть, несколько более длинную по сравнению с кратчайшей. Приближённые методы решения довольно часто применяются в различных приложениях задачи поиска кратчайших сетей. Среди них — конструирование интегральных электронных схем, построение эволюционного дерева для группы биологических видов и минимизация расхода материалов на создание сетей телефонных линий, трубопроводов и шоссейных дорог.
В общей форме задача Штейнера была впервые сформулирована в статье Милоша Кёсслера и Войцеха Ярника, опубликованной в 1934 году, однако сама эта проблема не приобрела широкой известности вплоть до 1941 года, когда Рихард Курант и Герберт Е. Роббинс включили её в свою книгу «Что такое математика?». Курант и Роббинс связали эту задачу с исследованиями Якоба Штейнера, немецкого математика XIX столетия, работавшего в Берлинском университете. Работа Штейнера была посвящена поиску одной точки, сумма расстояний от которой до всех точек заданного множества была бы минимальной. Однако ещё в 1640 году впервые была поставлена задача, являющаяся частным случаем обеих описанных задач — той, над которой работал Штейнер, и той, которая носит его имя: найти точку P, сумма расстояний от которой до каждой из трёх заданных точек минимальна. Эванджелиста Торричелли и Бонавентура Кавальери независимо друг от друга решили эту задачу. Торричелли и Кавальери доказали, чту суммарное расстояние минимально, когда все сопряжённые углы в точке P больше или равны 120°.
Зная, что углы с вершинами в точке P должны быть не меньше 120°, Торричелли и Кавальери придумали процедуру геометрического построения для нахождения точки P (см. рис.).
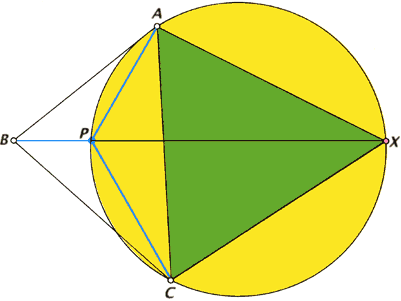
Кратчайшая сеть для трёх точек A, B и C. На самой длинной стороне треугольника ABC строится равносторонний треугольник ACX (зелёный цвет), и вокруг него описывается окружность (жёлтый цвет). На пересечении её с отрезком BX находится точка P, называемая точкой Штейнера. Отрезки AP, BP и CP образуют три сопряжённых угла по 120° и кратчайшую сеть, причём их суммарная длина равна BX.
Нужно провести отрезки прямых, соединяющие исходные точки (назовем их A, B и C), с точкой в вершине наибольшего угла (скажем, B). Если угол B больше или равен 120°, то искомая точка P совпадает с точкой B. Другими словами, кратчайшая сеть в данном случае представляет собой просто два отрезка прямых между точками A и B и точками B и C. Если угол в точке B меньше 120°, то точка P должна находиться где-то внутри треугольника. Чтобы найти её, следует построить равносторонний треугольник с основанием на самой большой стороне треугольника ABC, а именно на отрезке AC. Третья вершина равностороннего треугольника (обозначим её X) находится на противоположной стороне от точки B относительно AC. Вокруг построенного равностороннего треугольника описываем окружность и проводим прямую, соединяющую точки B и X. Точка P будет на пересечении этой прямой и окружности. Соединив точки A, B и C с точкой P, мы получаем три угла, в точности равные 120° каждый, и искомую кратчайшую сеть. Более того, длина отрезка BX оказывается равной длине кратчайшей сети. В дальнейшем в нашей статье мы будем называть точку X замещающей точкой, поскольку замена точек A и C одной точкой X не изменяет длину сети.
Задача с тремя точками и задача Штейнера для многих точек имеют много общих свойств. Их решения, имеющие вид дерева, характерны тем, что при удалении любого отрезка из кратчайшей сети мы должны будем исключить одну из заданных точек. Другими словами, мы не можем пройти по сети из какой-либо заданной точки и вернуться в неё, без того чтобы не пройти те или иные отрезки повторно. По этой причине графические решения задачи с тремя точками и задачи со многими точками называются деревьями Штейнера. Отрезки прямых называются рёбрами, а точки, роль которых аналогична точке P и которые нужно добавить для построения дерева, называются точками Штейнера.
Задача Штейнера для трёх точек даёт также некоторую информацию о геометрии кратчайших деревьев Штейнера. Во-первых, каждый угол равен 120° или больше, а это означает, что каждая точка соединяется с остальным деревом не более чем тремя рёбрами. Во-вторых, в каждой точке Штейнера сходятся ровно три ребра, образуя друг с другом углы, в точности равные 120°. В-третьих, число рёбер дерева всегда на единицу меньше суммарного числа заданных исходных точек и точек Штейнера. И наконец, последнее свойство: поскольку в каждой точке Штейнера сходятся ровно три ребра и по крайней мере одно ребро должно касаться каждой из заданного множества точек, максимальное число точек Штейнера для любой задачи на две меньше, чем число заданных исходных точек.
a
b
c
8
7, 464...
6, 928...
d
e
f
10
9, 928...
9, 196...
g
h
i
10
9, 327...
9, 250...
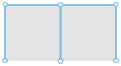
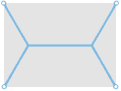
Задача поиска сети для точек, расположенных в вершинах равностороннего треугольника, прямоугольника и «лестницы» имеет различные решения. В случаях a, d и g точки соединяются без дополнительных промежуточных точек и такое решение называется минимальным остовным деревом. Деревья Штейнера, полученные путём добавления узловых точек, показаны для случаев b, c, e, f, h и i. Только c, f и i являются кратчайшими деревьями Штейнера, или кратчайшими сетями. Числа под каждым решением указывают примерную суммарную длину отрезков сети.
При одном и том же количестве и расположении исходных точек можно построить много различных деревьев Штейнера, удовлетворяющих перечисленным выше условиям. Некоторые из этих деревьев, называемые локально минимальными решениями, невозможно сократить за счёт мелкомасштабных изменений, таких как небольшое перемещение ребра или расщепление точки Штейнера. Однако не всякое локально минимальное дерево Штейнера даёт кратчайшее из возможных решений задачи. Для того чтобы преобразовать сеть в кратчайшее дерево, называемое глобально минимальным деревом Штейнера, могут потребоваться крупномасштабные перемещения точек Штейнера.
Рассмотрим для примера множество исходных точек, образующих четыре угла прямоугольника, размерами три метра на четыре. Решения содержат две точки Штейнера, которые можно расположить двумя различными способами. При каждом расположении мы получаем дерево Штейнера, причём в каждой точке Штейнера сходятся по три ребра под углом 120°. Если точки Штейнера расположить на линии, параллельной поперечной стороне прямоугольника, то получается локально минимальное дерево Штейнера длиной 9, 9 м. Если расположить точки Штейнера на линии, параллельной продольной стороне прямоугольника, то получится глобально минимальное дерево длиной 9, 2 м.
Действуя методом полного перебора, можно найти кратчайшую сеть путём построения всех возможных локально минимальных деревьев Штейнера, вычислением их длины и выбором кратчайшего. Но поскольку расположение точек Штейнера неоднозначно, возникает сомнение в том, что вычислить все локально минимальные деревья Штейнера можно за конечное время. З. Мелзак из Университета Британской Колумбии сумел преодолеть это затруднение и составил первый алгоритм для решения задачи Штейнера.
В алгоритме Мелзака рассматриваются многие возможные соединения между заданными точками и многие возможные расположения точек Штейнера. Алгоритм можно условно разбить на две части. В первой его части множество исходных точек просто подразделяется на всевозможные подмножества. Во второй части для каждого такого подмножества создается ряд возможных деревьев Штейнера с использованием построения, аналогичного тому, которое мы применили к задаче с тремя точками.
Так же как и для трёх точек, вместо двух исходных точек можно подставить одну заменяющую их точку, не изменяя результата (длины сети) решения. Однако в общем случае алгоритм должен угадать, какую пару следует заменить, и поэтому он перебирает все возможные пары. Более того, заменяющая точка может размещаться по любую сторону от прямой, соединяющей две заменяемые точки, поскольку равносторонний треугольник, используемый при построении, может быть ориентирован в одном из двух направлений. После того как одна из точек в подмножестве заменена одной из двух возможных заменяющих точек, на каждом последующем шаге алгоритма замещаются либо две другие исходные точки, либо одна исходная и одна замещающая, либо две замещающие другой замещающей точкой; и так до тех пор, пока всё подмножество не будет сведено к трём точкам.
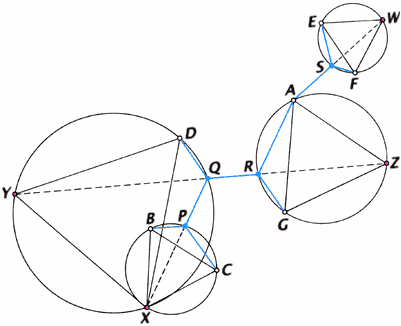
Как только для этих трёх точек найдена точка Штейнера, алгоритм начинает работать в обратном направлении, пытаясь определить точку Штейнера, соответствующую каждой замещающей точке (см. рис.).
Алгоритм Мелзака разбивает задачу поиска кратчайшей сети на подзадачи. Точка A подходит для разбиения задачи на подзадачи из 3 и 5 точек. Чтобы построить возможные деревья Штейнера для 5 точек, пару точек (например, B и C) можно заменить одной (здесь X), построив равносторонний треугольник с основанием BC. Теперь задача сведена к 4 точкам: X, D, G и A. Пару точек опять можно заменить — сначала D и X на Y, а потом G и A на Z. Вокруг каждого из полученных равносторонних треугольников (XDY, AGZ и BCX) описываем окружности. Точки Q и R, в которых прямая YZ пересекает две окружности, — это точки Штейнера, а пересечение прямой XQ с третьей окружностью определяет точку Штейнера P. Поскольку невозможно заранее предугадать наилучшее разбиение на подзадачи и группировки на пары, необходимо рассмотреть все варианты, чтобы найти кратчайшее дерево.
Попытка может окончиться неудачей, поскольку на расположение точек Штейнера накладываются противоречащие друг другу ограничения. Однако успешная попытка приводит к возникновению дерева Штейнера, соединяющего каждую исходную точку подмножества с деревом одним ребром. Рассмотрев, таким образом, все замещающие последовательности, алгоритм выбирает кратчайшее из этих деревьев Штейнера для подмножества. Комбинируя между собой всевозможными способами кратчайшие деревья Штейнера для подмножеств так, чтобы охватить исходное множество точек, можно построить всевозможные локально минимальные деревья Штейнера и определить геометрию кратчайшей сети.
Алгоритм Мелзака может потребовать колоссального времени даже для небольших задач, поскольку в нём рассматривается очень много вариантов. Например, задача для 10 точек может быть распределена на 512 подмножеств исходных точек. И хотя двухточечные подмножества не требуют большого объёма работы, каждое из 45 подмножеств с восемью точками имеет два миллиона замещающих последовательностей. Кроме того, существуют ещё более 18 000 способов объединить эти подмножества в деревья.
Разумеется, исследователи нашли более эффективные пути организации вычислений и сумели повысить быстродействие алгоритма. Вместо того чтобы рассматривать геометрию задачи, они фокусируют внимание на возможных конфигурациях соединений в сети, т.е. на её топологии. Топология указывает, какие точки соединены друг с другом, а не действительные расположения точек Штейнера. Приняв определённую топологию, можно найти соответствующую замещающую цепочку относительно быстро. При такой организации процесса скорость вычисления кратчайших деревьев Штейнера для подмножеств немного возрастает. Например, для подмножества из 8 точек алгоритм должен рассмотреть лишь около 10 000 различных топологий вместо двух миллионов различных последовательностей замещения.
Так как количество возможных топологий быстро возрастает с размером подмножества, задачи Штейнера могут стать менее трудоёмкими лишь в том случае, если требуется рассматривать только очень небольшие подмножества исходного множества точек. Эксперименты, проведённые с алгоритмом Мелзака, показали, что кратчайшая сеть для числа случайных точек больше 6 обычно может быть разбита на кратчайшие сети для меньших наборов точек. Однако, рассмотрев специальные конфигурации точек, называемые лестницами, Ф. Чанг из фирмы Bell Communications Research совместно с одним из авторов настоящей статьи (Грэмом) показал, что существуют бесконечно большие множества точек, для которых кратчайшее дерево Штейнера невозможно расчленить. Лестница — это конфигурация, в которой исходные точки расположены равномерно вдоль двух параллельных линий. Для этой весьма частной задачи Штейнера было найдено общее решение. Оно показало, что число точек Штейнера в кратчайшем дереве Штейнера для лестницы с нечётным количеством «ступенек» максимально: оно равно числу исходных точек минус 2. Такое дерево Штейнера невозможно расчленить, потому что для каждой точки Штейнера нужно одновременно учитывать все исходные точки. Следовательно, не всегда можно сократить размер подмножеств, рассматриваемых алгоритмом Мелзака.
Некоторым исследователям удалось улучшить эффективность алгоритмов по сравнению с алгоритмом Мелзака за счёт применения более тонких способов, позволяющих уменьшить объём вычислений (см. рис.).
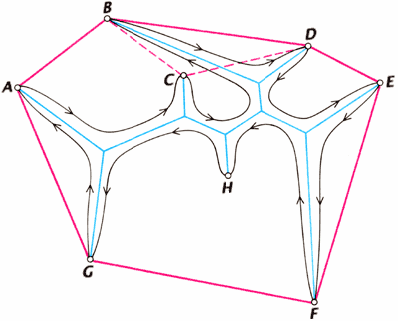
Методы усечения повышают эффективность алгоритмов поиска кратчайших сетей. Один из приёмов усечения, или исключения, возможных сетей (изобретённый Кокейном) заключается в том, чтобы рассмотреть порядок, в котором резиновое кольцо (красный цвет), натянутое вокруг заданного множества точек, касается их. Резинка касается всех точек, за исключением C и H, но C можно включить в последовательность, поскольку угол, образуемый точкой C с двумя соседними точками, находящимися в контакте с резинкой, не меньше 120°. Тогда порядок точек будет ABCDEFG. Непрерывный путь (чёрный цвет), проходящий вдоль возможной сети (синий цвет), касается точек в порядке ACBDEFHG. Поскольку B и C здесь переставлены местами по отношению к последовательности, образованной резинкой, эту сеть можно исключить из рассмотрения.
В их алгоритмах производится усечение вычислительной процедуры, т.е. прекращаются те ветви вычисления, которые заведомо должны привести к сравнительно длинным сетям. Новые методы усечения действительно значительно сокращают объём вычислений. Программы, основанные на алгоритме Мелзака, как, скажем, программа Э. Кокейна из Университета Виктории, написанная в 1969 году, могли решить любую задачу для 9 точек и некоторые задачи для 12 точек приблизительно за полчаса. Программа же, недавно написанная Кокейном и его коллегой из Университета Виктории Д. Хьюджиллом, использует мощный метод усечения, изобретённый Р. Винтером из Копенгагенского университета. Эта программа смогла решить все задачи для 17 точек и большинство случайно сгенерированных задач для 30 точек всего за несколько минут. Метод усечения Винтера оказался настолько удачным, что благодаря устранению большинства возможных топологий, основной объём вычислительной работы связан с комбинированием решений, полученных для отдельных подмножеств.
Однако для всех этих программ время решения задачи может сильно зависеть от геометрии и от количества точек. Более того, время вычислений даже для самых изощрённых алгоритмов растёт по экспоненциальному закону с ростом числа точек, и задачи Штейнера для 100 точек остаются практически неразрешимыми. Будет ли когда-нибудь найден эффективный алгоритм, позволяющий решать большие задачи Штейнера?
Прогресс, достигнутый в теории вычислительной математики, убедил большинство исследователей, что существующие алгоритмы решения задачи Штейнера практически невозможно улучшить. В этой теории каждой задаче сопоставляется определённый размер. Для каждого конкретного случая задачи Штейнера таким естественным размером является число заданных исходных точек. Затем рассматривается количество элементарных компьютерных операций — таких как сложение, вычитание и умножение, — которое может потребоваться алгоритму для решения какого-то частного случая задачи определённого размера. Поскольку различные частные случаи одного и того же размера могут потребовать различного количества операций, следует рассматривать максимальное количество операций как функцию размера задачи. Если число операций растет с размером задачи (n) пропорционально некоторой степени размера, например, как в выражениях n2, 5n или 6n + n10, то процедура решения называется алгоритмом с полиномиальным временем, или просто полиномиальным алгоритмом. Такие алгоритмы считаются эффективными, по крайней мере в теоретическом смысле. Если же количество операций возрастает экспоненциально с размером задачи, как, например, в случаях 2n, 5n или 3n2·4n, процедура решения называется алгоритмом с экспоненциальным временем или просто экспоненциальным алгоритмом.
Хотя для очень маленьких задач и полиномиальные, и экспоненциальные алгоритмы достаточно практичны, для больших задач время решения у экспоненциальных алгоритмов настолько велико, что практически они оказываются безнадёжными (см. H. Lewis, C. Papadimitriou. The Efficiency of Algorithms, Scientific American, January, 1978). Для достаточно больших задач полиномиальный алгоритм, выполняющийся даже на самой медленной машине, даёт решение всё-таки значительно быстрее, чем экспоненциальный алгоритм, выполняющийся на суперкомпьютере.
Хотя для задачи Штейнера были найдены экспоненциальные алгоритмы (например, алгоритм Мелзака), ни одного полиномиального алгоритма найти для неё не удалось. И шансы на то, что эффективный алгоритм будет когда-нибудь найден, очень малы. В 1971 году С. Кук из Университета в Торонто доказал, что если будет найден полиномиальный алгоритм для любой задачи, принадлежащей классу труднорешаемых задач, называемых NP-полными, то этим же алгоритмом можно будет воспользоваться для эффективного решения широкого класса труднорешаемых задач, включая класс NP-полных. Позже один из авторов настоящей статьи (Грэм), работая совместно с М. Гэри и Д. жонсоном из AT&T Bell Laboratories, доказал, что задача Штейнера относится к классу NP-полных. Поскольку до сегодняшнего дня все NP-полные задачи оказались не по силам тысячам исследователей, то маловероятно, чтобы какая-нибудь NP-полная задача, в том числе и задачи Штейнера, была решена алгоритмом с полиномиальным временем. Однако доказательство того, что NP-полные задачи невозможно решить эффективным способом, остаётся одной из основных теоретических проблем вычислительной математики.
Хотя представляется очень маловероятным, чтобы появился эффективный алгоритм с полиномиальным временем, вычисляющий кратчайшие сети, существуют практичные алгоритмы, отыскивающие несколько более длинные сети. Одним из примеров является в этом смысле алгоритм, решающий задачу минимального остовного дерева, который отыскивает кратчайшую систему прямолинейных отрезков, связывающих данное множество точек без добавления новых. Чтобы решить эту задачу, нужно соединить две точки, ближе всего расположенные друг к другу, и на каждом последующем шаге соединять ближайшую пару точек, которую можно соединить, не образуя замкнутого пути. В конце концов, можно удалить одно ребро из замкнутого пути, и заданные исходные точки останутся всё же связанными остающимися рёбрами.
Е. Гилберт и X. Поллак высказали предположение о том, что отношение длины кратчайшего дерева Штейнера к длине минимального остовного дерева равно, самое меньшее, √3/2, т.е. дерево Штейнера не более чем на 13, 4% короче минимального остовного дерева. Это отношение √3/2 возникает в простом примере, когда три исходные точки являются вершинами равностороннего треугольника. Хотя это предположение остаётся недоказанным, Чанг и один из авторов данной статьи (Грэм) показали, что дерево Штейнера короче минимального остовного дерева не более чем на 17, 6%.
Минимальные остовные деревья можно часто укоротить на 3 или 4% путём тщательного выбора дополнительных точек Штейнера и небольшой переделки дерева. Одному из авторов (Берну) удалось показать, что этот неточный алгоритм до какой-то степени оправдан в теоретическом смысле, поскольку в среднем длина модифицированного дерева будет немного меньше средней длины минимального остовного дерева.
Задачи отыскания минимального остовного дерева и кратчайшей сети решались в применении к планированию топологии телефонных сетей, трубопроводов и шоссейных дорог. Решения, приближённые или точные, помогают спланировать геометрию сети и подсчитать необходимые количества материалов. В более сложных формулировках задачи Штейнера можно учитывать такие факторы, как необходимость избежания определённых географических свойств местности, а также отыскивать кратчайшие соединения между узлами уже существующих сетей.
Возможно, наиболее важным практическим применением задачи Штейнера является конструирование интегральных электронных схем. Более короткая сеть проводящих линий на интегральной схеме требует меньшего времени зарядки-разрядки по сравнению с более длинной сетью и повышает, таким образом, быстродействие схемы. Однако задача отыскания кратчайшей сети на интегральной схеме имеет другую геометрию, так как проводники на ней обычно проходят лишь в двух направлениях — горизонтальном и вертикальном.
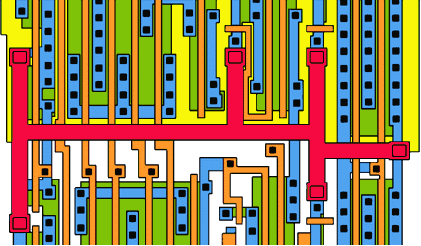
Разновидности задачи о кратчайшей сети применялись при конструировании электронных интегральных схем, с тем чтобы повысить их быстродействие. Кратчайшая сеть из вертикальных и горизонтальных проводников, связывающих множество выводов, выделена красным цветом. Здесь показаны также проводники и выводы в более глубоких слоях схемы.
Такая задача, получившая название прямоугольной задачи Штейнера, была впервые изучена в 1965 году Морисом Хэнаном из Исследовательского центра им. Томаса Уотсона корпорации IBM в Йорктаун-Хейтсе (шт. Нью-Йорк). Как и в классической задаче Штейнера, решение для прямоугольной её версии также содержит точки Штейнера и исходные точки, но рёбра встречаются в них под углом либо 90°, либо 180°. Хотя точки Штейнера могут, казалось бы, лежать повсеместно в прямоугольной задаче, так же как и в классической задаче Штейнера, Хэнан показал, что в кратчайшей прямоугольной сети на расположение точек Штейнера можно наложить определённые ограничения. Через каждую исходную точку проводятся горизонтальная и вертикальная прямые, и каждое пересечение двух линий даёт возможное положение точки Штейнера. Чтобы найти кратчайшую сеть, алгоритм может рассмотреть все подмножества возможных точек Штейнера. Однако по мере того, как число исходных точек возрастает, время решения для каждого алгоритма, осуществляющего полный перебор вариантов, растёт экспоненциально. Более тонкие, но всё же экспоненциальные алгоритмы способны решать прямоугольные задачи Штейнера размером порядка 40 точек.
Прямоугольная версия задачи поиска минимального остовного дерева может быть эффективно решена алгоритмом, выбирающим на каждом шаге кратчайшее соединение, если это соединение не образует замкнутого пути. Ф. Хванг из фирмы Bell Laboratories показал, что прямоугольное дерево Штейнера не бывает короче прямоугольного остовного дерева более чем на одну треть.
Наиболее удивительное применение задача Штейнера нашла в биологии, в одной из областей, изучающей происхождение видов. Д. Сэнкофф из Монреальского университета и ряд других исследователей сформулировали одну из версий задачи Штейнера для того, чтобы вычислять наиболее вероятные филогенетические деревья. Учёные сначала изолируют какой-то определённый белок, общий для организмов, которые они намереваются классифицировать. Затем для каждого организма они определяют последовательность аминокислот, составляющих этот белок, и устанавливают точку в позиции, определяемой числом различий между белком соответствующего организма и белком других организмов. Организмы с похожими последовательностями аминокислот определяются, таким образом, как близкие, а организмы с непохожими последовательностями — как далёкие. В кратчайшей сети для этого абстрактного множества исходных точек точки Штейнера соответствуют наиболее вероятным предкам, а рёбра представляют связь между данным организмом и предком, обладающую наименьшим числом мутаций. Однако, поскольку филогенетическая задача Штейнера не легче других задач подобного рода, эта задача — за исключением случаев с небольшим числом организмов — послужила скорее в качестве мысленного эксперимента, нежели практического инструмента исследований.
Хотя за последние годы наши познания в области алгоритмов значительно расширились, задача поиска кратчайшей сети остаётся всё такой же неприступной. Несмотря на то что формулировка этой задачи очень проста, её решения трудно поддаются анализу. Крошечное изменение геометрии задачи, кажущееся несущественным, может коренным образом изменить кратчайшую сеть, являющуюся её решением. Такая чувствительность к исходным данным делает даже периферийные вопросы, касающиеся кратчайших сетей, весьма не простыми. Задача поиска кратчайшей сети будет ещё долгие годы привлекать наше воображение.
Список литературы
1. E. N. Gilbert and H. О. Pollak. Steiner Minimal Trees. In: SIAM Journal on Applied Mathematics, 1968, v. 16, No 1, pp. 1–29.
2. Z. A. Melzak. Companion to Concrete Mathematics. John Wiley & Sons, Inc., 1973.
3. Pawel Winter. An Algorithm for the Steiner Problem in the Euclidean Plane. In: Networks, 1985, v. 15, No 3, pp. 323–345.
4. Pawel Winter. Steiner Problem in Networks: A Survey. In: Networks, 1987, v. 17, No 2, pp. 129–167.
5. М. Гэри, Д. Джонсон. Вычислительные машины и труднорешаемые задачи. — Перев. с англ. М.: Мир, 1982.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ