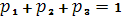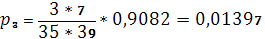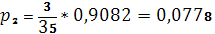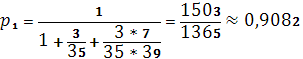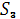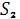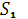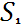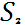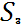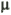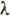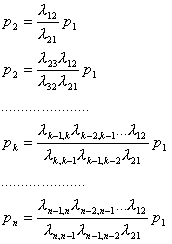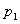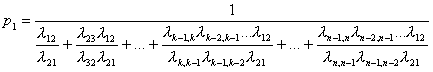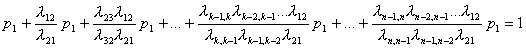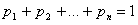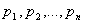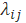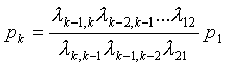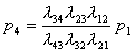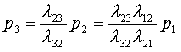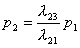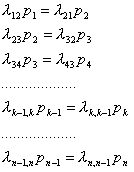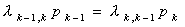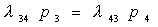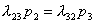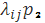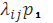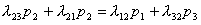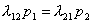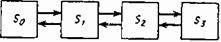Применение марковских процессов гибели и размножения
Оглавление
Введение
В данной теоретико-практической работе будет рассмотрена схема непрерывных марковских цепей – так называемая «схема гибели и размножения»
Данная тема крайне актуальна ввиду высокой значимости марковских процессов в исследовании экономических, экологических и биологических процессов, кроме того, марковские процессы лежат в основе теории массового обслуживания, которая в настоящее время активно используется в различных экономических направлениях, в том числе управлении процессами на предприятии.
Марковские процессы гибели и размножения находят широкое применение в объяснении различных процессов происходящих в биосфере, экосистеме и т.д. Надо отметить, что данный тип марковских процессов получил свое название именно вследствие широкого применения в биологии, в частности моделируя гибель и размножение особей различных популяций.
В данной работе будут использованы процессы гибели и размножения при решении задачи, целью которой является нахождение приблизительного количества пчел в отдельно взятой популяции.
Теоретическая часть
В рамках теоретической части будут написаны алгебраические уравнения для предельных вероятностей состояний. Очевидно, что если две непрерывные цепи Маркова имеют одинаковые графы состояний и различаются только значениями интенсивностей ,
Рис. 1.1
то можно сразу найти предельные вероятности состояний для каждого из графов в отдельности, достаточно составить и решить в буквенном виде уравнения для одного из них, а затем подставить вместо соответствующие значения. Для многих часто встречающихся форм графов линейные уравнения легко решаются в буквенном виде.
В данной работе будет описана схема непрерывных марковских цепей — так называемая «схема гибели и размножения».
Марковская непрерывная цепь называется «процессом гибели и размножения», если ее граф состояний имеет вид, представленный на рис. 1.1, т. е. все состояния можно вытянуть в одну цепочку, в которой каждое из средних состояний (S2, ..., Sn-1) связано прямой и обратной связью с каждым из соседних состояний, а крайние состояния (S1, Sn) — только с одним соседним состоянием.
Для записи алгебраических уравнений для предельных вероятностей состояний возьмем некую задачу.
Пример. Техническое устройство состоит из трех одинаковых узлов; каждый из них может выходить из строя (отказывать); отказавший узел немедленно начинает восстанавливаться. Состояния системы нумеруем по числу неисправных узлов:
S0— все три узла исправны;
S1— один узел отказал (восстанавливается), два исправны;
S2— Два узла восстанавливаются, один исправен;
S3— все три узла восстанавливаются.
Граф состояний показан на рис. 1.2. Из графа видно, что процесс, протекающий в системе, представляет собой процесс «гибели и размножения».
Рис. 1.2
Схема гибели и размножения очень часто встречается в самых разнообразных практических задачах; поэтому имеет смысл заранее рассмотреть эту схему в общем виде и решить соответствующую систему алгебраических уравнений с тем, чтобы в дальнейшем, встречаясь с конкретными процессами, протекающими по такой схеме, не решать задачу каждый раз заново, а пользоваться уже готовым решением.
Итак, рассмотрим случайный процесс гибели и размножения с графом состояний, представленным на рис. 1.3
Рис. 1.3
Напишем алгебраические уравнения для вероятностей состояний. Для первого состояния S1 имеем:
(1.2)
Для второго состояния S2 суммы членов, соответствующих входящим и выходящим стрелкам, равны:
Но, в силу (1.2), можно сократить справа и слева равные друг другу члены и получим:
и далее, совершенно аналогично,
…
Одним словом, для схемы гибели и размножения члены, соответствующие стоящим друг над другом стрелкам, равны между собой:
(1.3)
где k принимает все значения от 2 до n.
Итак, предельные вероятности состояний ръ р2> ..., рп в любой схеме гибели и размножения удовлетворяют уравнениям:
(1.4)
и нормировочному условию:
(1.5)
Решим эту систему следующим образом: из первого уравнения (1.4) выразим р2:
(1.6)
из второго, с учетом (1.6), получим
(1.7)
из третьего, с учетом (1.7):
и вообще
(1.8)
Эта формула справедлива для любого k от 2 до п.
Обратим внимание на ее структуру. В числителе стоит произведение всех плотностей вероятности перехода (интенсивностей) стоящих у стрелок, направленных слева направо, с начала и вплоть до той, которая идет в состояние Sk; в знаменателе — произведение всех интенсивностей , стоящих у стрелок, идущих справа налево, опять-таки, с начала и вплоть до стрелки, исходящей из состояния Sk. При k=n в числителе будет стоять произведение интенсивностей , стоящих у всех стрелок, идущих слева направо, а в знаменателе — у всех стрелок, идущих справа налево.
Итак, все вероятности выражены через одну из них: . Подставим эти выражения в нормировочное условие: . Получим:
откуда
(1.9)
Остальные вероятности выражаются через
(1.10)
Таким образом, задача «гибели и размножения» решена в общем виде: найдены предельные вероятности состояний.
Практическая часть
Процессы Маркова, в частности гибели и размножения, используют для описания работы и анализа широкого класса систем с конечным числом состояний, в которых происходят неоднократные переходы из одного состояния в другое под воздействием каких-либо причин. В таких системах они происходят случайным образом, скачкообразно в произвольный момент времени, когда наступают некоторые события (потоки событий). Как правило, они бывают двух типов: одно из них условно называют рождением объекта, а второе — его гибелью.
Естественное размножение пчелиных семей — роение — с точки зрения протекающих в системе в текущий момент времени процессов можно рассматривать как вероятностный процесс, когда семья в определенный момент времени может перейти из рабочего состояния в роевое. В зависимости от различных факторов, как контролируемых технологических, так и слабоконтролируемых биологических и климатических, оно может закончиться роением или возвратом семьи в рабочее состояние. При этом семья может неоднократно переходить то в одно, то в другое состояние. Таким образом, для описания математической модели процесса роения допустимо применять теорию однородных процессов Маркова.
Интенсивность перехода пчелиной семьи в роевое состояние — размножение — в значительной мере определяется темпами накопления молодых бездеятельных пчел. Интенсивность обратного перехода — «гибели» — возвращением семьи в рабочее состояние, которая, в свою очередь, зависит собственно от роения, отбора расплода и пчел (формирование отводков), количества собираемого нектара и т.д.
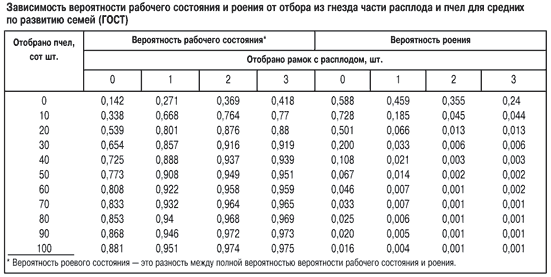
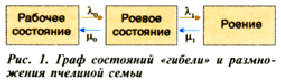
Вероятность перехода пчелиной семьи в роевое состояние в первую очередь будет определяться интенсивностью проходящих в ней процессов, приводящих к роению λ, и противороевых приемов μ, которые зависят от технологий, используемых для снижения ройливости семей. Следовательно, чтобы влиять на обсуждаемые процессы, необходимо изменить интенсивность и направленность потоков λ и μ (рис. 1).
Моделирование отбора из семьи части пчел (увеличения их «гибели») показало, что вероятность возникновения рабочего состояния логарифмически возрастает, а вероятность роения логарифмически сокращается. При противороевом приеме — отборе из семьи 5–7 тыс. пчел (две-три стандартные рамки) — вероятность роения составит 0,05, а вероятность рабочего состояния — 0,8; отбор более трех рамок с пчелами снижает вероятность роения на очень малую величину.
Решим практическую задачу, касающуюся процесса роения у пчел.
Для начала построим граф, похожий на граф на рис 1, с интенсивностями перехода в то или иное состояние.
ЗАДАЧА 1
7 3
39 35
Где - это рабочее состояние, - роевое состояние, - роение.
Имея интенсивности перехода в то или иное состояние, можем найти предельные вероятности состояний для данного процесса.
Используя формулы, приведенные в теоретической части находим:
Получив предельные вероятности состояний, можем свериться с таблицей с целью нахождения приблизительного числа особей (сот шт. пчел) и количество отобранных рамок с расплодом, получаем, что, скорее всего, было отобрано 5000 пчел и одна рамка с расплодом.
Заключение
Подведем итог.
В данной работе была приведена теоретическая справка, а также практическое применение марковским процессам гибели и размножения на примере пчелиной популяции, также была решена практическая задача с использованием марковского процесса гибели и размножения.
Было показано, что марковские процессы имеют прямое отношение ко многим процессам, происходящим в окружающей среде и в экономике. Также марковские процессы лежат в основе теории массового обслуживания, которая в свою очередь является незаменимой в экономике, в частности при управлении предприятием и различными процессами, происходящими в нем.
Собственные мысли
На мой взгляд марковские процессы гибели и размножения безусловно полезны в различных сферах деятельности человека, но у них есть ряд недостатков, в частности система из любого своего состояния непосредственно может перейти только в соседнее с нею состояние. Данный процесс не отличается особой сложностью и сфера его применения немного узко-специализирована, но, тем не менее, данный процесс может использоваться в сложных моделях в качестве одного из компонента новой модели, например при моделировании документооборота в компании, задействовании станков в цеху и так далее.
Список литературы
Е.С. Вентцель «Исследование операций» Москва, «Советское радио» 1972
Л.Г.Лабскер «Вероятностное моделирование в финансово-экономической области» Москва «Альпина Паблишер» 2002
И.Н.Мишин Статья: «Роение в процессах маркова» 2006
В.Н.Тутубалин, Ю.М.Барабашева «Процессы размножения и гибели в экологических моделях» 2006

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ