Прогнозирование урожайности различными методами
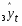
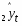
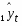
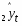

Содержание
1. Задание
2. Аналитическое выравнивание
3. Метод экспоненциального сглаживания
4. Метод скользящих средних
5. Выравнивание при помощи рядов Фурье
Выводы
1. Задание
По имеющимся исходным данным урожайности озимой пшеницы в Волгоградский области провести расчеты прогнозных значений на последующие шесть лет для выявления закономерных или случайных изменений.
Исходные данные урожайности:
1947
1948
1949
1950
1951
1952
1953
1954
1955
1956
1957
1958
3,5
5,2
2,2
3,6
7,1
6,9
4,1
5,3
10,1
4,8
7,7
16,8
1
2
3
4
5
6
7
8
9
10
11
12
1959
1960
1961
1962
1963
1964
1965
1966
1967
1968
1969
9,8
14,5
13,7
19,0
5,0
12,0
11,3
17,5
13,1
17,9
9,6
13
14
15
16
17
18
19
20
21
22
23
2. Аналитическое выравнивание
Выберем в качестве функций регрессии – линейную, параболическую, гиперболическую и показательную:
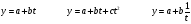
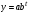 .
.
Гиперболическую и показательную можно линеаризовать и применить МНК к этим функциям как к линейным. Для гиперболической функции введем новую переменную:
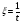 .
.
Тогда получим:
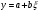 ,
,
где
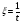 .
.
Для показательной функции проведем следующие преобразования. Прологарифмируем обе части уравнения: 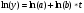 . Сделаем замены:
. Сделаем замены:
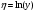 ,
, 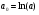 ,
, 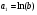 .
.
Получим:
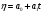 ,
,
откуда найдем: 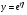 ,
, 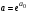 ,
, 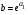 .
.
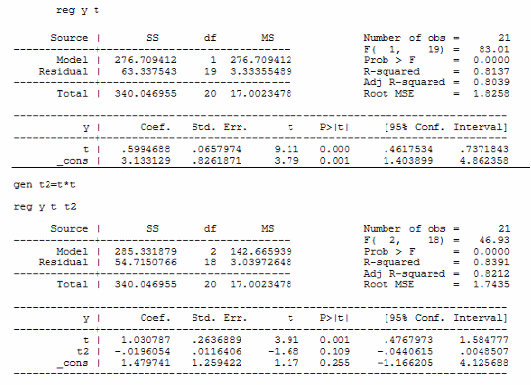
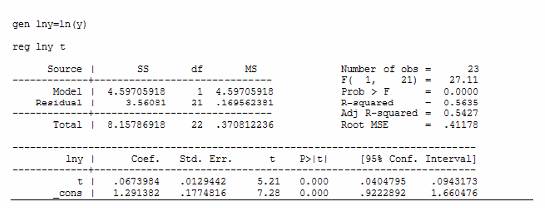
Применим ПО MS Excel 2003 и Stata 7.0. Посчитаем коэффициент корреляции:
Коэффициент корреляции значим.
Построим линейную регрессию
Регрессионная статистика
Множественный R
0,717687
R-квадрат
0,515074
Нормированный R-квадрат
0,491982
Стандартная ошибка
3,693991
Наблюдения
23
Дисперсионный анализ
df
SS
MS
F
Значимость F
Регрессия
1
304,3725
304,3725
22,30559
0,000116
Остаток
21
286,557
13,64557
Итого
22
590,9296
Коэффициенты
Стандартная ошибка
t-статистика
P-Значение
Нижние 95%
Верхние 95%
Y-пересечение
3,014625
1,592152
1,893427
0,072162
-0,29644
6,325686
Переменная X 1
0,548419
0,11612
4,722879
0,000116
0,306935
0,789903
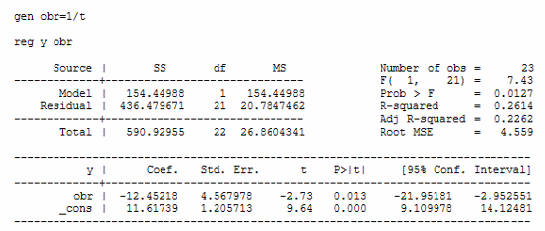
Регрессия для гиперболической функции:
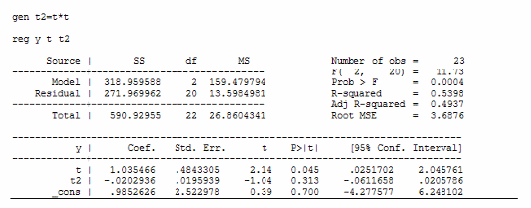
Регрессия для параболической функции:
Регрессия для показательной функции:
Как видно из этих данных, коэффициент детерминации у регрессии для гиперболической функции значительно хуже, чем у других моделей. А константа и коэффициент при переменной 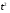 в модели параболической регрессии не значимы согласно t-критерию Стьюдента.
в модели параболической регрессии не значимы согласно t-критерию Стьюдента.
Коэффициенты детерминации для моделей линейной и показательной регрессий примерно одиноковы, причем R-квадрат больше у показательной регрессии. Сравним эти 2 модели по другим показателям. Рассчитаем среднюю квадратическую ошибку уравнения тренда и информационные критерии Акейка и Шварца:
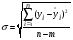 ,
, 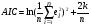 ,
, 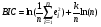
Чем меньше значение информационных критериев, тем лучше модель.
Итак, для модели линейной регрессии получим:
AIC=5,131843277
BIC=2,658769213 σ=3,694
Для модели регрессии показательной функции имеем:
AIC= 5,477785725 BIC= 2,831740437 σ=4,028
Все 3 показателя лучше в первом случае.
Применим модель линейной регрессии для аналитического выравнивания исходного ряда. Модель такова:
у=3,01+0,55t;
Значения уровней ряда, полученных по модели, и остатков представлены в следующей таблице:
-
Наблюдение
Предсказанное Y
Остатки
1
3,563043478
-0,063043478
2
4,111462451
1,088537549
3
4,659881423
-2,459881423
4
5,208300395
-1,608300395
5
5,756719368
1,343280632
6
6,30513834
0,59486166
7
6,853557312
-2,753557312
8
7,401976285
-2,101976285
9
7,950395257
2,149604743
10
8,498814229
-3,698814229
11
9,047233202
-1,347233202
12
9,595652174
7,204347826
13
10,14407115
-0,344071146
14
10,69249012
3,807509881
15
11,24090909
2,459090909
16
11,78932806
7,210671937
17
12,33774704
-7,337747036
18
12,88616601
-0,886166008
19
13,43458498
-2,13458498
20
13,98300395
3,516996047
21
14,53142292
-1,431422925
22
15,0798419
2,820158103
23
15,62826087
-6,02826087
Спрогнозируем урожайность озимой пшеницы на последующие 6 лет
-
Прогнозные значения
t
y
24
16,17667984
25
16,72509881
26
17,27351779
27
17,82193676
28
18,37035573
29
18,9187747
Из графика видно, что урожайность с каждым последующим годом будет возрастать и достигнет через шесть лет значения практически в 2 раза большего, чем в 1969 году. Этот результат достигнут в результате существенного роста урожайности зерновых культур.
Проверим наличие автокорреляции в данном динамическом ряду. Для этого составим следующие таблицы:
Расчет коэффициента автокорреляции 1-го порядка
Год
Фактические уровни y(t)
Уровни, сдвинутые на год y(t-1)
y(t)y(t-1)
y(t)^2
1
3,5
9,6
33,6
12,25
2
5,2
3,5
18,2
27,04
3
2,2
5,2
11,44
4,84
4
3,6
2,2
7,92
12,96
5
7,1
3,6
25,56
50,41
6
6,9
7,1
48,99
47,61
7
4,1
6,9
28,29
16,81
8
5,3
4,1
21,73
28,09
9
10,1
5,3
53,53
102,01
10
4,8
10,1
48,48
23,04
11
7,7
4,8
36,96
59,29
12
16,8
7,7
129,36
282,24
13
9,8
16,8
164,64
96,04
14
14,5
9,8
142,1
210,25
15
13,7
14,5
198,65
187,69
16
19
13,7
260,3
361
17
5
19
95
25
18
12
5
60
144
19
11,3
12
135,6
127,69
20
17,5
11,3
197,75
306,25
21
13,1
17,5
229,25
171,61
22
17,9
13,1
234,49
320,41
23
9,6
17,9
171,84
92,16
Сумма
220,7
220,7
2353,68
2708,69
Средняя
9,595652174
102,333913
117,76913
Дисперсия
25,69258979
Автокорреляция присутствует ( с вероятностью 0,95)
Коэффициент автокорреляции
0,399234662
Расчет коэффициента автокорреляции 2-го порядка
Год
Фактические уровни y(t)
Уровни, сдвинутые на 2 года y(t-2)
y(t)y(t-2)
y(t)^2
1
3,5
17,9
62,65
12,25
2
5,2
9,6
49,92
27,04
3
2,2
3,5
7,7
4,84
4
3,6
5,2
18,72
12,96
5
7,1
2,2
15,62
50,41
6
6,9
3,6
24,84
47,61
7
4,1
7,1
29,11
16,81
8
5,3
6,9
36,57
28,09
9
10,1
4,1
41,41
102,01
10
4,8
5,3
25,44
23,04
11
7,7
10,1
77,77
59,29
12
16,8
4,8
80,64
282,24
13
9,8
7,7
75,46
96,04
14
14,5
16,8
243,6
210,25
15
13,7
9,8
134,26
187,69
16
19
14,5
275,5
361
17
5
13,7
68,5
25
18
12
19
228
144
19
11,3
5
56,5
127,69
20
17,5
12
210
306,25
21
13,1
11,3
148,03
171,61
22
17,9
17,5
313,25
320,41
23
9,6
13,1
125,76
92,16
Сумма
220,7
220,7
2349,25
2708,69
Средняя
9,595652174
102,141304
117,76913
Дисперсия
25,69258979
Автокорреляция присутствует ( с вероятностью 0,99)
Коэффициент автокорреляции
0,391737999
Расчет коэффициента автокорреляции 3-го порядка
Год
Фактические уровни y(t)
Уровни, сдвинутые на 3 года y(t-3)
y(t)y(t-3)
y(t)^2
1
3,5
13,1
45,85
12,25
2
5,2
17,9
93,08
27,04
3
2,2
9,6
21,12
4,84
4
3,6
3,5
12,6
12,96
5
7,1
5,2
36,92
50,41
6
6,9
2,2
15,18
47,61
7
4,1
3,6
14,76
16,81
8
5,3
7,1
37,63
28,09
9
10,1
6,9
69,69
102,01
10
4,8
4,1
19,68
23,04
11
7,7
5,3
40,81
59,29
12
16,8
10,1
169,68
282,24
13
9,8
4,8
47,04
96,04
14
14,5
7,7
111,65
210,25
15
13,7
16,8
230,16
187,69
16
19
9,8
186,2
361
17
5
14,5
72,5
25
18
12
13,7
164,4
144
19
11,3
19
214,7
127,69
20
17,5
5
87,5
306,25
21
13,1
12
157,2
171,61
22
17,9
11,3
202,27
320,41
23
9,6
17,5
168
92,16
Сумма
220,7
220,7
2218,62
2708,69
Средняя
9,595652174
96,4617391
117,76913
Дисперсия
25,69258979
Автокорреляция отсутствует
Коэффициент автокорреляции
0,170679504
Как видно из таблиц, обнаружилась автокорреляция только первого и второго порядков. Это говорит о том, что значительное влияние на урожайность озимой пшеницы в данном году оказывает урожайность двух предыдущих лет.
3. Метод экспоненциального сглаживания
Выберем теперь форму зависимости (линейную или параболическую) методом экспоненциального сглаживания.
Рассчитаем начальные условия экспоненциального сглаживания для линейной тенденции:
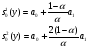 ,
,
где 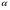 – параметр сглаживания;
– параметр сглаживания;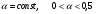 .
.
Выберем 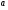 =0,3
=0,3
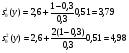
На основе расчета начальных условий определяем оценки коэффициентов и характеристики сглаженных значений.
Формулы расчета оценок коэффициентов:
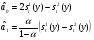
Формулы расчета характеристик сглаживания динамического ряда:
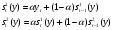
Расчет оценок коэффициентов, характеристик сглаженных значений, прогнозных значений по линейной форме экспоненциального сглаживания (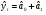 ) и квадратов ошибок сведем в таблицу:
) и квадратов ошибок сведем в таблицу:
S1
S2
a0
a1
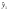
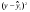
3,5
3,692
4,2548
3,1292
-0,3752
2,754
0,556516
5,2
4,2952
4,27096
4,31944
0,01616
4,3356
0,74718736
2,2
3,45712
3,945424
2,968816
-0,325536
2,64328
0,196497158
3,6
3,514272
3,772963
3,255581
-0,1724608
3,08312
0,267164934
7,1
4,9485632
4,243203
5,653923
0,47024
6,1241632
0,95225746
6,9
5,7291379
4,837577
6,620699
0,594373888
7,21507264
0,099270768
4,1
5,0774828
4,933539
5,221426
0,095962266
5,31738842
1,482034555
5,3
5,1664897
5,026719
5,30626
0,093180119
5,39943995
0,009888303
10,1
7,1398938
5,871989
8,407798
0,845269727
9,25306811
0,717293628
4,8
6,2039363
6,004768
6,403105
0,13277883
6,53588335
3,013291001
7,7
6,8023618
6,323806
7,280918
0,319037494
7,5999555
0,010008902
16,8
10,801417
8,11485
13,48798
1,791044614
15,2790286
2,313354018
9,8
10,40085
9,02925
11,77245
0,914400039
12,6868503
8,333904844
14,5
12,04051
10,23375
13,84727
1,204503986
15,0517701
0,304450249
13,7
12,704306
11,22197
14,18664
0,988220769
15,174858
2,17520614
19
15,222584
12,82222
17,62295
1,600243488
19,2231924
0,049814834
5
11,13355
12,14675
10,12035
-0,67546729
9,44488196
19,75697565
12
11,48013
11,8801
11,08016
-0,26664841
10,8135091
1,407760654
11,3
11,408078
11,69129
11,12486
-0,18880986
10,9360534
0,132457117
17,5
13,844847
12,55271
15,13698
0,861421592
15,9984008
2,254800093
13,1
13,546908
12,95039
14,14342
0,397677461
14,5411018
2,076774272
17,9
15,288145
13,88549
16,6908
0,93510118
17,6258978
0,075132009
9,6
13,012887
13,53645
12,48932
-0,34904247
12,1402807
6,453026248
53,38506621
Определим начальные условия экспоненциального сглаживания при параболической тенденции:
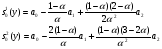
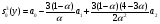
Выберем 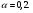
Соответственно: 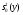 = -3,5166014;
= -3,5166014; 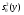 =-8,3384654;
=-8,3384654; 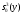 =-13,4803294
=-13,4803294
На основе расчета начальных условий определяем оценки коэффициентов и характеристики сглаженных значений. Расчет оценок коэффициентов, характеристик сглаженных значений, прогнозных значений по параболической форме экспоненциального сглаживания и квадратов ошибок сведем в таблицу:
yi
Характеристики
Оценки коэффициентов
S1
S2
S3
a0
a1
a2
3,5
-2,1132811
-7,09343
-12,2029
2,737493
1,176307311
-0,00808583
3,91383304
0,171257789
5,2
-0,6506249
-5,80487
-10,9233
4,539396
1,307567679
0,002236112
5,84696599
0,41856499
2,2
-0,0804999
-4,65999
-9,67067
4,067818
0,915810984
-0,02694854
4,98399185
7,7506106
3,6
0,6556001
-3,59688
-8,45591
4,301519
0,740885761
-0,03790978
5,04312342
2,082605212
7,1
1,9444801
-2,4886
-7,26245
6,036806
0,927243389
-0,02129738
6,96427656
0,018420853
6,9
2,935584
-1,40377
-6,09071
6,927341
0,900178696
-0,02172458
7,82775603
0,860731248
4,1
3,1684672
-0,48932
-4,97043
6,002929
0,477055074
-0,05145785
6,4813078
5,670626841
5,3
3,5947738
0,327499
-3,91085
5,890979
0,300937696
-0,06069189
6,19375797
0,798803306
10,1
4,895819
1,241163
-2,88044
8,083524
0,66559622
-0,02918445
8,74954607
1,823725828
4,8
4,8766552
1,968261
-1,9107
6,814478
0,21148275
-0,06066067
7,02780093
4,963096995
7,7
5,4413242
2,662874
-0,99599
7,339363
0,226893959
-0,05502572
7,56777081
0,017484558
16,8
7,7130593
3,672911
-0,06221
12,05824
1,172083885
0,01906433
13,2305026
12,741312
9,8
8,1304475
4,564418
0,863117
11,5612
0,819644091
-0,00845449
12,3808846
6,660965133
14,5
9,404358
5,532406
1,796975
13,41283
1,040514466
0,008532533
14,4533811
0,00217332
13,7
10,263486
6,478622
2,733304
14,0879
0,967225013
0,002471645
15,0551249
1,836363466
19
12,010789
7,585056
3,703655
16,98086
1,395610031
0,034020784
18,3770439
0,388074354
5
10,608631
8,189771
4,600878
11,85746
-0,01686454
-0,07312702
11,8432687
46,83032672
12
10,886905
8,729198
5,426542
11,89966
-0,06882696
-0,07155927
11,8333975
0,027756394
11,3
10,969524
9,177263
6,176686
11,55347
-0,19385244
-0,07551973
11,3624686
0,003902328
17,5
12,275619
9,796934
6,900736
14,33679
0,397867259
-0,02609459
14,7349986
7,645232881
13,1
12,440495
10,32565
7,585718
13,93026
0,196638702
-0,03906748
14,1276666
1,056098587
17,9
13,532396
10,967
8,261974
15,95817
0,567175299
-0,00872643
16,5253867
1,88956183
9,6
12,745917
11,32278
8,874135
13,14354
-0,18901755
-0,06409432
12,956581
11,26663598
114,9243312
Определим начальные условия экспоненциального сглаживания при параболической тенденции:

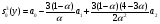
Выберем 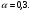
Соответственно:
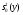 = 1,91758335
= 1,91758335
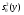 =-1,2595453
=-1,2595453
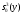 =-4,60049885
=-4,60049885
На основе расчета начальных условий определяем оценки коэффициентов и характеристики сглаженных значений.
Расчет оценок коэффициентов, характеристик сглаженных значений, прогнозных значений по параболической форме экспоненциального сглаживания (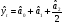 ) и квадратов ошибок сведем в таблицу:
) и квадратов ошибок сведем в таблицу:
yi
Характеристики
Оценки коэффициентов
S1
S2
S3
a0
a1
a2
3,5
4,0123083
0,322011
-3,12375
7,947147
1,813620275
0,04491565
9,76177562
0,742657215
5,2
5,7486158
1,949992
-1,60162
9,794246
1,862385849
0,045368582
11,6576611
3,450904714
2,2
5,9440311
3,148204
-0,17668
8,210805
0,696151358
-0,09717296
8,91167811
6,308526949
3,6
5,9308218
3,982989
1,071224
6,914721
-0,07996759
-0,17704896
6,8504266
0,903310726
7,1
7,9915752
5,185565
2,305526
10,72356
1,132323907
-0,01359714
11,8559729
0,891187203
6,9
8,6841027
6,235126
3,484406
10,83134
0,76321248
-0,05542235
11,5960834
1,679832129
4,1
8,6888719
6,97125
4,530459
9,683325
0,049851182
-0,13282693
9,74199756
1,085758914
5,3
9,0822103
7,604538
5,452683
9,8857
-0,00649776
-0,12382952
9,88686868
0,012798695
10,1
10,857547
8,580441
6,39101
13,22233
1,059105338
0,01610373
14,2815645
0,516149625
4,8
9,910283
8,979393
7,167525
9,960194
-0,43707812
-0,16181241
9,53620743
3,371657732
7,7
12,007198
9,887735
7,983588
14,34198
1,112672366
0,039547931
15,4554323
2,086775904
16,8
13,055039
10,83793
8,83989
15,49123
1,158089937
0,040238477
16,650127
1,322792148
9,8
14,238527
11,85811
9,745355
16,88662
1,274192695
0,049163686
18,162018
1,35028586
14,5
15,666969
13,00077
10,72198
18,72059
1,510309073
0,07115812
20,23343
1,521349651
13,7
17,026878
14,2086
11,76796
20,2228
1,56621064
0,069363232
21,791418
2,532611258
19
17,978815
15,33966
12,83947
20,75693
1,262936101
0,025523494
22,0201889
3,313087501
5
15,34517
15,34132
13,59003
13,60159
-1,65662782
-0,32095738
11,9964693
7,820240766
12
16,531619
15,69841
14,22254
16,72218
-0,25277423
-0,11803844
16,4763703
7,972884921
11,3
16,612133
15,97252
14,74754
16,66636
-0,28139592
-0,10751882
16,3907461
0,167488742
17,5
18,018493
16,58632
15,29917
19,5957
0,751423356
0,0266386
20,347482
0,907290518
13,1
16,092945
16,4383
15,64091
14,60483
-1,23246052
-0,20989346
13,3944003
3,219872312
17,9
16,845062
16,56033
15,91674
16,77093
-0,21852822
-0,06591395
16,5545712
4,183779005
9,6
16,321543
16,4887
16,08832
15,58687
-0,61020409
-0,10423889
14,9820974
0,013901034
55,37514352
Определим начальные условия экспоненциального сглаживания при параболической тенденции:

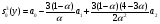
Выберем 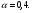
Соответственно:
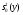 = 3,0313761
= 3,0313761
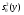 =1,06416203
=1,06416203
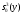 =-0,970755225
=-0,970755225
На основе расчета начальных условий определяем оценки коэффициентов и характеристики сглаженных значений.
Расчет оценок коэффициентов, характеристик сглаженных значений, прогнозных значений по параболической форме экспоненциального сглаживания (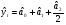 ) и квадратов ошибок сведем в таблицу:
) и квадратов ошибок сведем в таблицу:
yi
Характеристики
Оценки коэффициентов
S1
S2
S3
a0
a1
a2
3,5
5,3788257
2,790027
0,533558
8,299952
2,24282099
0,147701582
10,5536813
2,734661735
5,2
7,1472954
4,532935
2,133309
9,976391
2,076938886
0,095437634
12,0578839
5,098039615
2,2
6,8483772
5,459112
3,46363
7,631426
-0,01682611
-0,26942947
7,65089649
1,564742023
3,6
6,4690263
5,863078
4,423409
6,241255
-0,89293167
-0,37054215
5,41697437
0,233313758
7,1
9,0014158
7,118413
5,50141
11,15042
1,669114
0,118222485
12,8265216
0,000703397
6,9
9,5208495
8,079388
6,532601
10,85699
0,797136961
-0,04681077
11,6552198
1,836620752
4,1
9,1925097
8,524636
7,329415
9,333035
-0,37506983
-0,23437677
8,98543167
0,081471237
5,3
9,5155058
8,920984
7,966043
9,749608
-0,16430499
-0,1601865
9,59813271
0,161497319
10,1
11,709303
10,03631
8,79415
13,81313
1,78550802
0,191480082
15,6169656
0,380646557
4,8
10,105582
10,06402
9,302098
9,426785
-1,09285126
-0,32015981
8,38518453
0,469477846
7,7
12,823349
11,16775
10,04836
15,01515
1,937829195
0,238313566
16,9813782
0,006622415
16,8
13,89401
12,25825
10,93232
15,83958
1,572441642
0,137696713
17,4215037
3,692176522
9,8
15,136406
13,40952
11,9232
17,10387
1,525483554
0,106920913
18,6350679
2,673447105
14,5
16,681843
14,71845
13,0413
18,93149
1,75420453
0,127220923
20,6937846
2,86890619
13,7
18,089106
16,06671
14,25146
20,31865
1,67049331
0,092065566
21,9933807
3,216214243
19
18,933464
17,21341
15,43624
20,5964
1,057851513
-0,02538566
21,6545716
2,115778599
5
15,040078
16,34408
15,79938
11,88738
-3,74509187
-0,82164528
8,47983483
0,518637869
12
16,744047
16,50407
16,08125
16,8012
-0,12441845
-0,08125883
16,6800788
6,863987211
11,3
16,766428
16,60901
16,29236
16,76461
-0,14275806
-0,07077229
16,6243542
0,030851434
17,5
18,579857
17,39735
16,73435
20,28188
1,596467573
0,230894027
21,9049998
0,366024715
13,1
15,787914
16,75358
16,74204
13,84506
-2,16385405
-0,43430858
11,7755167
0,030806121
17,9
16,912748
16,81724
16,77212
17,05863
0,142041992
0,022392189
17,2009276
1,957403589
9,6
16,187649
16,56541
16,68944
15,55616
-0,64652505
-0,11276768
14,9159978
0,033856812
36,93588706
Постоим соответственно графики значений 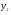 по исходным данным линейной и параболической формы сглаживания.
по исходным данным линейной и параболической формы сглаживания.
Линейная форма:
Параболическая форма:
1) 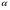 =0,2
=0,2
2) 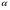 =0,3
=0,3
3) 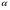 =0,4
=0,4
Видно,что параболическая форма зафисимости экспоненциального сглаживания лучше подогнана к исходным данным.Следовательно, параболическая форма более подходит для прогноза. Сделаем прогноз на 6 лет и представим графической формой.
t
24
25
26
27
28
29
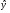
14,916
14,28855
13,67381
13,0718
12,4825
11,90591
4. Метод скользящих средних
Выберем в качестве параметров скольжения 3, 5, 9. Причем при параметре, равном 5, используем весовые коэффициенты для расчета скользящей средней. Для определения этих весовых коэффициентов применим треугольник Паскаля. Таким образом, весовыми коэффициенты будут следующие числа: 1, 2, 4, 2, 1.
Для начала проведем расчеты при параметре скольжения 3. Данные приведем в следующей таблице:
t
y
Скользящая сумма
Скользящая средняя
Прирост
Ускорения
1
3,5
2
5,2
25,1
8,367
3
2,2
22,1
7,367
-1
4
3,6
25,1
8,367
1
2
5
7,1
29
9,667
1,3
0,3
6
6,9
31,8
10,6
0,933
-0,367
7
4,1
29
9,667
-0,933
-1,867
8
5,3
33,7
11,233
1,567
2,500
9
10,1
32,7
10,9
-0,333
-1,900
10
4,8
39,6
13,2
2,300
2,633
11
7,7
40,1
13,367
0,167
-2,133
12
16,8
49,4
16,467
3,100
2,933
13
9,8
51,5
17,167
0,700
-2,400
14
14,5
56,2
18,733
1,567
0,867
15
13,7
59,4
19,8
1,067
-0,500
16
19
49,6
16,533
-3,267
-4,333
17
5
48,7
16,233
-0,300
2,967
18
12
45,3
15,1
-1,133
-0,833
19
11,3
57,4
19,133
4,033
5,167
20
17,5
49,7
16,567
-2,567
-6,600
21
13,1
51,5
17,167
0,600
3,167
22
17,9
45,3
15,1
-2,067
-2,667
23
9,6
Построим модель регрессии на ряд скользящих средних. Сравним модели линейной регрессии и параболической:
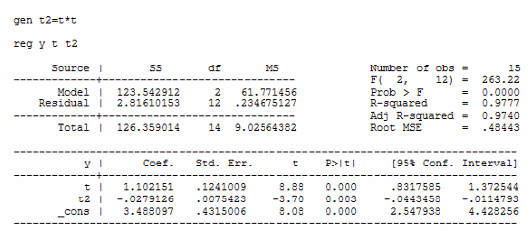
Выберем модель параболической регрессии на основании лучших коэффициента детерминации и скорректированного коэффициента детерминации у этой модели. Получим следующую модель:
y=1.4+1.03t-0.02 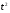
Спрогнозируем значения скользящих средних на последующие 6 лет:
-
t
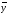
23
16,4389
24
16,0816
25
15,6469
26
15,1348
27
14,5454
28
13,8786
Рассчитаем значения исходного ряда на будущий период, используя формулу:
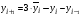
и приведем в следующей таблице:
Значения скользящих средних, полученные по модели
t
Значения у
1
3,5
8,51976912
2
5,2
9,052236652
3
2,2
9,584704185
4
3,6
10,11717172
5
7,1
10,64963925
6
6,9
11,18210678
7
4,1
11,71457431
8
5,3
12,24704185
9
10,1
12,77950938
10
4,8
13,31197691
11
7,7
13,84444444
12
16,8
14,37691198
13
9,8
14,90937951
14
14,5
15,44184704
15
13,7
15,97431457
16
19
16,50678211
17
5
17,03924964
18
12
17,57171717
19
11,3
18,1041847
20
17,5
18,63665224
21
13,1
19,16911977
22
17,9
16,3222
23
9,6
Прогноз на будущее
16,9218
24
21,47
17,5214
25
19,70
18,1209
26
11,40
18,7205
27
23,27
19,3201
28
21,50
29
13,20
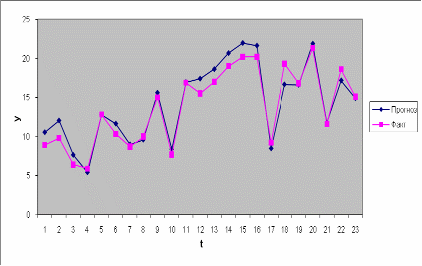
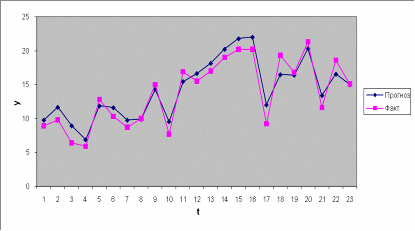
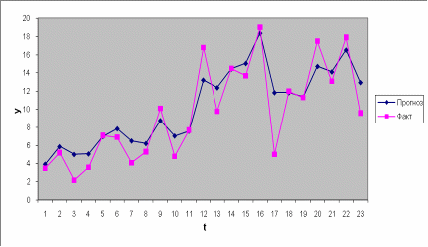
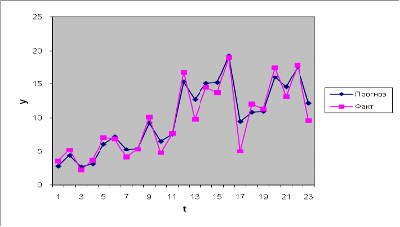
Значения урожайности по годам вместе с прогнозными значениями представим на графике:
Проведем расчеты для параметра 5 с применением треугольника Паскаля.
t
y
Скользящая сумма
Скользящая средняя
Прирост
Ускорения
1
3,5
2
5,2
3
2,2
37
3,700
4
3,6
45,1
4,510
0,81
5
7,1
55,7
5,570
1,06
0,25
6
6,9
58,9
5,890
0,320
-0,740
7
4,1
58
5,800
-0,090
-0,410
8
5,3
61,3
6,130
0,330
0,420
9
10,1
72,4
7,240
1,110
0,780
10
4,8
76,9
7,690
0,450
-0,660
11
7,7
93,9
9,390
1,700
1,250
12
16,8
121,5
12,150
2,760
1,060
13
9,8
123,2
12,320
0,170
-2,590
14
14,5
140,8
14,080
1,760
1,590
15
13,7
136,6
13,660
-0,420
-2,180
16
19
139,9
13,990
0,330
0,750
17
5
107
10,700
-3,290
-3,620
18
12
117,1
11,710
1,010
4,300
19
11,3
122,3
12,230
0,520
-0,490
20
17,5
148,7
14,870
2,640
2,120
21
13,1
144,1
14,410
-0,460
-3,100
22
17,9
23
9,6
Построим модель регрессии на ряд скользящих средних. Сравним модели линейной регрессии и параболической:
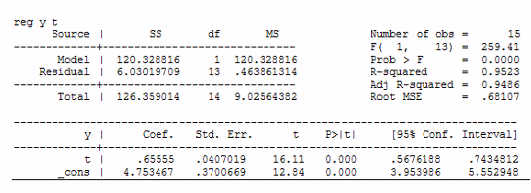
Выберем модель параболической регрессии на основании лучших R-квадрата и скорректированного R-квадрата у этой модели. Получим следующую модель:
y=1.88+1.11t-0.02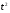
Отобразим ее на графике:
Спрогнозируем значения скользящих средних на последующие 6 лет:
-
t
23
17,1962
24
17,8133
25
18,4303
26
19,0474
27
19,6644
28
20,2815
Рассчитаем значения исходного ряда на будущий период, используя формулу:
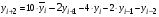
и приведем в следующей таблице:
-
Значения скользящих средних, полученные по модели
t
Значения у
1
3,5
2
5,2
8,8125
3
2,2
9,3924
4
3,6
9,9723
5
7,1
10,5522
6
6,9
11,1321
7
4,1
11,7120
8
5,3
12,2919
9
10,1
12,8718
10
4,8
13,4517
11
7,7
14,0316
12
16,8
14,6115
13
9,8
15,1914
14
14,5
15,7713
15
13,7
16,3512
16
19
16,9311
17
5
17,5109
18
12
18,0908
19
11,3
18,6707
20
17,5
19,2506
21
13,1
15,9621
22
17,9
16,5792
23
9,6
Прогноз на будущее
17,1962
24
25,12
17,8133
25
28,25
18,4303
26
-22,12
19,0474
27
49,53
28
92,10
29
-175,87
Из таблицы видно, что при t=29 значение урожайности отрицательное, чего не может быть в принципе. Этот факт объясняется тем, что исходный ряд плохо аппроксимируется нормальным распределением.
Проведем расчеты при параметре скольжения 9. Данные приведем в следующей таблице:
-
t
y
Скользящая сумма
Скользящая средняя
Прирост
Ускорения
1
3,5
2
5,2
3
2,2
4
3,6
5
7,1
48
5,333
6
6,9
49,3
5,478
0,144
7
4,1
51,8
5,756
0,278
0,133
8
5,3
66,4
7,378
1,622
1,344
9
10,1
72,6
8,067
0,689
-0,933
10
4,8
80
8,889
0,822
0,133
11
7,7
86,8
9,644
0,756
-0,067
12
16,8
101,7
11,300
1,656
0,900
13
9,8
101,4
11,267
-0,033
-1,689
14
14,5
103,3
11,478
0,211
0,244
15
13,7
109,8
12,200
0,722
0,511
16
19
119,6
13,289
1,089
0,367
17
5
115,9
12,878
-0,411
-1,500
18
12
124
13,778
0,900
1,311
19
11,3
119,1
13,233
-0,544
-1,444
20
17,5
21
13,1
22
17,9
23
9,6
Построим модель регрессии на ряд скользящих средних. Сравним модели линейной регрессии и параболической:
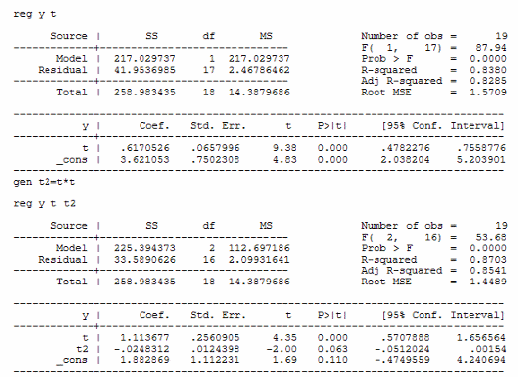
Выберем модель параболической регрессии на основании лучших R-квадрата и скорректированного R-квадрата у этой модели. Получим следующую модель:
y=3.49+1.1t-3.49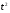
Спрогнозируем значения скользящих средних на последующие 6 лет:
-
t
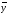
23
17,8644
24
18,5200
25
19,1756
26
19,8311
27
20,4867
28
21,1422
Рассчитаем значения исходного ряда на будущий период, используя формулу:
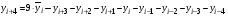
и приведем в следующей таблице:
Значения скользящих средних, полученные по модели
t
Значения у
1
3,5
2
5,2
3
2,2
4
3,6
9,9721
5
7,1
10,5981
6
6,9
11,2241
7
4,1
11,8501
8
5,3
12,4761
9
10,1
13,1021
10
4,8
13,7281
11
7,7
14,3541
12
16,8
14,9801
13
9,8
15,6061
14
14,5
16,2321
15
13,7
16,8580
16
19
17,4840
17
5
18,1100
18
12
18,7360
19
11,3
15,2422
20
17,5
15,8978
21
13,1
16,5533
22
17,9
17,2089
23
9,6
Прогноз на будущее
16,6847
24
51,99
16,2773
25
18,31
26
3,56
27
9,82
28
8,38
29
13,83
5. Выравнивание при помощи рядов Фурье
Пусть ряд содержит циклическую составляющую, выраженную некоторой функцией от времени y(t) c известными периодами, нацело делящими n. То есть периоды y(t) задаются числами n/kj, j=1, …, m, где (k1, …,km) – подмножество последовательности целых чисел 1, …, (n-1)/2, если n нечетное. Представим y(t) в виде ряда Фурье – линейной комбинации синусов и косинусов для n нечетного:
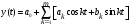
Рассмотрим теперь задачу гармонического анализа ряда, состоящую в оценивании параметров a0, ak, bk:
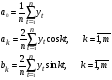
Последовательные значения t определяются 0 с увеличением, равным 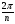 .
.
Расчет показателей, необходимых для выравнивания с помощью ряда Фурье, представлен в следующей таблице:
-
Год
t
y
y cos t
y sin t
y cos 2t
y sin 2t
1
0
3,5
3,5
0
7,765
18,192
3,5
0
8,132
21,456
2
0,273
5,2
5,007
1,403
6,611
1,992
4,443
2,702
6,252
1,107
3
0,546
2,2
1,880
1,143
5,679
12,103
1,012
1,953
4,698
6,242
4
0,820
3,6
2,457
2,631
5,037
2,065
-0,246
3,592
3,721
0,015
5
1,093
7,1
3,266
6,304
4,733
5,602
-4,094
5,800
3,464
13,220
6
1,366
6,9
1,403846
6,756
4,790
4,452
-6,329
2,749
3,938
8,775
7
1,639
4,1
-0,280
4,090
5,203
1,217
-4,062
-0,558
5,016
0,839
8
1,912
5,3
-1,775
4,994
5,942
0,412
-4,111
-3,345
6,474
1,379
9
2,185
10,1
-5,824
8,251
6,952
9,910
-3,382
-9,517
8,049
4,207
10
2,459
4,8
-3,723
3,029
8,158
11,276
0,977
-4,700
9,500
22,090
11
2,732
7,7
-7,06253
3,068
9,471
3,135
5,256
-5,627
10,667
8,803
12
3,005
16,8
-16,644
2,288
10,792
36,090
16,177
-4,533
11,495
28,143
13
3,278
9,8
-9,709
-1,334
12,026
4,953
9,437
2,644
12,030
4,971
14
3,551
14,5
-13,300
-5,777
13,0785
2,021
9,897
10,597
12,383
4,482
15
3,825
13,7
-10,627
-8,646
13,873
0,030
2,787
13,413
12,680
1,040
16
4,098
19
-10,9569
-15,522
14,350
21,618
-6,363
17,903
13,008
35,905
17
4,371
5
-1,674
-4,711
14,475
89,779
-3,879
3,155
13,374
70,119
18
4,644
12
-0,819
-11,972
14,238
5,009
-11,888
1,634
13,698
2,884
19
4,917
11,3
2,299
-11,064
13,657
5,553
-10,364
-4,502
13,836
6,430
20
5,190
17,5
8,051
-15,538
12,774
22,336
-10,092
-14,297
13,620
15,056
21
5,464
13,1
8,941446
-9,574
11,656
2,087
-0,894
-13,069
12,922
0,032
22
5,737
17,9
15,294
-9,301
10,3844
56,485
8,235
-15,893
11,702
38,410
23
6,010
9,6
9,244
-2,590
9,055
0,297
8,202
-4,988
10,041
0,194
n=23
∑
220,7
-21,050
-52,072
220,7
316,615
4,219
-14,886
220,700
295,799
Год
t
y
y cos 3t
y sin 3t
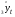
(yi-yi2)
1
0
3,5
3,5
0
6,496
8,976
2
0,273
5,2
3,549
3,800
3,47017
2,992
3
0,546
2,2
-0,150
2,195
2,5366
0,113
4
0,820
3,6
-2,793
2,272
3,55156
0,002
5
1,093
7,1
-7,034
-0,967
5,39523
2,906
6
1,366
6,9
-3,979
-5,637
6,74298
0,025
7
1,639
4,1
0,834
-4,014
6,91425
7,920
8
1,912
5,3
4,528
-2,754
6,26056
0,923
9
2,185
10,1
9,725
2,725
5,85861
17,989
10
2,459
4,8
2,208
4,262
6,72393
3,702
11
2,732
7,7
-2,579
7,255
9,06763
1,870
12
3,005
16,8
-15,409
6,693
12,0877
22,206
13
3,278
9,8
-8,989
-3,904
14,4381
21,512
14
3,551
14,5
-4,856
-13,663
15,0781
0,334
15
3,825
13,7
6,303
-12,164
13,9511
0,063
16
4,098
19
18,295
-5,126
12,0474
48,339
17
4,371
5
4,272
2,598
10,7918
33,545
18
4,644
12
2,441
11,749
11,1343
0,749
19
4,917
11,3
-6,516
9,232
12,9175
2,616
20
5,190
17,5
-17,337
2,383
14,9303
6,603
21
5,464
13,1
-10,162
-8,267
15,6291
6,396
22
5,737
17,9
-1,222
-17,858
14,0876
14,534
23
6,010
9,6
6,553
-7,016
10,5895
0,979
n=23
∑
220,7
-18,815
-26,207
220,7
205,297
Рассчитаем параметры:
a0
a1
b1
a2
b2
a3
b3
9,596
-1,830
-4,528
0,367
-1,294
-1,636
-2,279
Таким образом, получили модели:
- для гармоники первого порядка 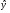 = 9,569-1,83 cos t-4.528 sin t
= 9,569-1,83 cos t-4.528 sin t
- для гармоники второго порядка 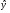 = 9,569-1,83 cos t-4.528 sin t +
= 9,569-1,83 cos t-4.528 sin t +
+ 0,367 соs 2t-1.294 sin 2t
- для гармоники третьего порядка 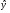 =9,569-1,83 cos t-4.528 sin t +
=9,569-1,83 cos t-4.528 sin t +
+ 0,367 соs 2t-1.294 sin 2t-1.636 cos3t-2.279 sin 3t
Исследуем модель с гармоникой первого порядка
Прогнозные значения
-
Год
t
24
6,283
7,765199
25
6,556
6,611
26
6,830
5,679
27
7,103
5,037
28
7,376
4,733
29
7,649
4,790
Изучим модель с гармоникой второго порядка
Прогнозные значения
-
Год
t
24
6,283
8,132054
25
6,556
6,252
26
6,830
4,698
27
7,103
3,721
28
7,376
3,464
29
7,649
3,938
Исследуем модель с гармоникой третьего порядка
Прогнозные значения
-
Год
t
24
6,283
6,496
25
6,556
3,470
26
6,830
2,537
27
7,103
3,552
28
7,376
5,395
29
7,649
6,743
Выводы
Были рассмотрены четыре метода прогнозирования – аналитическое выравнивание методом наименьших квадратов, метод экспоненциального сглаживания, метод скользящих средних, и выравнивание при помощи рядов Фурье. Выберем наиболее подходящий метод, который дает наиболее правдоподобный прогноз.
Выравнивание с помощью рядов Фурье дает сумму квадратов ошибок от 200 до 300 (в зависимости от гармоники). Метод экспоненциального сглаживания дает результат получше: для параболического тренда сумма квадратов ошибок колеблется от 36 до 115 (при 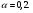 сумма квадратов ошибок равна 115; при
сумма квадратов ошибок равна 115; при 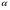 =0,4 сумма квадратов ошибок 36);Для линейной тенденции сумма квадратов ошибок равна 55. Аналитическое выравнивание МНК дает сумму квадратов ошибок, равную 272. Лучше всего описывает тренд метод скользящих средних с параметром n=3. Он дает сумму квадратов ошибок, равную 63.
=0,4 сумма квадратов ошибок 36);Для линейной тенденции сумма квадратов ошибок равна 55. Аналитическое выравнивание МНК дает сумму квадратов ошибок, равную 272. Лучше всего описывает тренд метод скользящих средних с параметром n=3. Он дает сумму квадратов ошибок, равную 63.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ