Расчет показателей надежности простейшей системы электроснабжения вероятностными методами
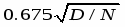 ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ
Кафедра: «Электроснабжение железнодорожного транспорта»
Дисциплина: «Основы теории надёжности»
Курсовая работа
«Расчет показателей надежности простейшей системы электроснабжения вероятностными методами»
Выполнил:
студент группы ЭНС-04-2
Иванов А. К.
Проверил:
канд. техн. наук, доцент
Герасимов Л. Н.
Иркутск 2008
Термины и определения, используемые в теории надежности, регламентированы ГОСТ 27.002-89 «Надежность в технике. Термины и определения».
Надежность – свойство объекта выполнять заданные функции, сохраняя во времени и в заданных пределах значения всех эксплуатационных параметров.
Надежность объекта характеризуется следующими основными состояниями и событиями:
Исправность – состояние объекта, при котором он соответствует всем требованиям, установленным нормативно-технической документацией.
Работоспособность – состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения основных параметров, установленных НТД.
Предельное состояние – состояние объекта, при котором его применение (использование) по назначению недопустимо или нецелесообразно.
Повреждение - событие, заключающееся в нарушении исправного состояния объекта при сохранении его работоспособного состояния.
Отказ – событие, заключающееся в нарушении работоспособного состояния объекта.
Критерий отказа – отличительный признак или совокупность признаков, согласно которым устанавливается факт возникновения отказа.
Для некоторых объектов предельное состояние является последним в его функционировании, т.е. объект снимается с эксплуатации, для других – определенной фазой в эксплуатационном графике, требующей проведения ремонтно-восстановительных работ. В связи с этим объекты могут быть разделены на два класса:
невосстанавливаемые, для которых работоспособность в случае возникновения отказа не подлежит восстановлению, или по каким-либо причинам нецелесообразна;
восстанавливаемые, работоспособность которых может быть восстановлена, в том числе и путем замены элементов.
К числу невосстанавливаемых объектов можно отнести, например, электронные и электротехнические детали (диоды, сопротивления, конденсаторы, изоляторы и другие элементы конструкций). Объекты, состоящие из многих элементов, например, трансформатор, выключатель, электронная аппаратура, являются восстанавливаемыми, поскольку их отказы связаны с повреждениями одного или нескольких элементов, которые могут быть отремонтированы или заменены. В ряде случаев один и тот же объект в зависимости от особенностей, этапов эксплуатации или назначения может считаться восстанавливаемым или невосстанавливаемым.
Введенная классификация играет важную роль при выборе моделей и методов анализа надежности.
Надежность является комплексным свойством, включающим в себя, в зависимости от назначения объекта или условий его эксплуатации, ряд
Составляющих (единичных) свойств, в соответствии с ГОСТ 27.002-89:
безотказность;
долговечность;
ремонтопригодность;
сохраняемость.
Безотказность – свойство объекта непрерывно сохранять работоспособность в течение некоторой наработки или в течение некоторого времени.
Долговечность – свойство объекта сохранять работоспособность до наступления предельного состояния при установленной системе технического обслуживания и ремонтов.
Ремонтопригодность – свойство объекта, заключающееся в его приспособленности к предупреждению и обнаружению причин возникновения отказов, поддержанию и восстановлению работоспособности путем проведения ремонтов и технического обслуживания.
Сохраняемость – свойство объекта непрерывно сохранять требуемые эксплуатационные показатели в течение (и после) срока хранения и транспортирования.
В зависимости от объекта надежность может определяться всеми перечисленными свойствами или частью их.
Наработка – продолжительность или объем работы объекта, измеряемая в любых неубывающих величинах (единица времени, число циклов нагружения, километры пробега и т. п.).
Показатель надежности количественно характеризует, в какой степени данному объекту присущи определенные свойства, обусловливающие надежность.
Задание на расчёт
Система электроснабжения, представленная на рис.1, включает в себя два энергорайона, питающихся от одного источника Г. Второй энергорайон получает питание по воздушной ЛЭП.
Г
А
Б
Т
ВЛ
В
Энергорайон №1 Энергорайон №2
Рис. 1. Схема системы электроснабжения
Первый энергорайон подключен через две подстанции А и Б, соединенные параллельно по низкой стороне. Каждая подстанций способна обеспечить питание данного энергорайона, поэтому нарушение электроснабжения наступает только при одновременном обесточивании подстанций А и Б.
Второй район имеет одну подстанцию В и отключается при всех отказах, ведущих к обесточиванию этой подстанции.
Требуется найти аналитическим методом и методом статистических испытаний (методом Монте-Карло)
вероятность безотказной работы (показатель безотказности) системы, зная вероятности безотказной работы отдельных ее элементов
абсолютную и относительную погрешности оценки искомого показателя надежности статистическим методом при разном числе испытаний.
Исходные данные
По результатам испытаний, или обработки статистики, получены вероятности
РГ = 0.95; РТ = 0.985; РВЛ = 0.89;
Так же определены вероятности безотказной работы трансформаторов подстанций
РА = РБ = РВ = 0.96.
Расчёт надёжности
Безотказная работа рассматриваемой части системы электроснабжения будет тогда, когда в соответствии с принятыми условиями в работоспособном состоянии находятся
все подстанции А и Б и В,
одна из подстанций А или Б, и подстанция В.
Одновременное обесточивание подстанций А и Б, или обесточивание подстанции В, так же как и одновременное обесточивание всех трех подстанций является отказом системы.
Для решения задачи требуется знать вероятности обесточивания подстанций. Подстанции обесточиваются, если повреждается (выходит из работы) хотя бы один из элементов системы в цепи, соединяющей соответствующую подстанцию (А и Б, или В) с источником генерируемой мощности, а также при отказе самого источника Г , или устройств подстанции.
Вероятности обесточивания подстанций могут быть вычислены по данным о надежности элементов цепи соединения, либо могут быть получены в результате обработки статистики (опытных данных) о функционировании подстанций в прошлом. Так, если за K лет собрана статистика о числе случаев обесточивания nj каждой j- ой подстанции и длительностях пребывания τi их в таком состоянии при i-ом обесточивании (i = 1.. nj ), то можно определить среднее время пребывания подстанций в обесточенном состоянии - τoi по формуле
τoi = 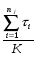 , {час\год} (1)
, {час\год} (1)
Соответственно, среднее время пребывания подстанций в работоспособном состоянии T0j определиться по формуле
T0j = Tгод - τoi , (2)
где T0j - календарное число часов в расчетном периоде – в данном случае, это один расчетный год, равный 8760 час.
Параметры T0j и τoi можно использовать для определения других показателей надежности подстанции. Так, вероятность безотказной работы подстанции вычисляется по формуле
Pj = T0j / Tгод , , здесь j = {Г, Т, А, Б, ВЛ, В} (3)
Определив по заданной статистике значения Pj,, рассчитаем функцию надежности системы в целом, которая, как показатель безотказности, соответствует вероятности ее безотказной работы.
Аналитический метод
Из большого числа применяющихся аналитических методов воспользуемся вероятностными, основанными на теоремах сложения и умножения для групп совместных и несовместных событий. В соответствии с этими теоремами, на первом этапе решения данной задачи определяются вероятности бесперебойного электроснабжения каждой из подстанций по вероятностям безотказной работы элементов, образующих последовательные цепочки связей подстанции с источником питания Г. Допустим, что по результатам испытаний, или обработки статистики, получены эти вероятности.
По вероятностям безотказной работы элементов из исходных данных найдём вероятности работоспособного состояния Vj для каждой из подстанций по формулам:
-
VА
=
РГ . РТ . РА
=
0.95 . 0.985 . 0.96.
=
0.898
VБ
=
РГ . РТ . РБ
=
0.95 . 0.985 . 0.96.
=
0.898
VВ
=
РГ . РТ . РВ . РВЛ
=
0.95 . 0.985 . 0.96 . 0.89
=
0.800
Полученные результаты показывают, что вероятность работоспособного состояния для подстанции В ниже, чем для А или Б, так как в цепочке связи от Г к В имеется дополнительный элемент - ВЛ, - надежность которого отражается на состоянии подстанции В. Подстанции А и Б находятся в одинаковых условиях , поэтому VА = VБ.
По полученным значениям VА, VБ, VВ вычисляются вероятности безотказного электроснабжения энергорайонов - V№1 и V№2 . Для энергорайона №1 схема замещения по надежности показана на рис. 2.
А А
Т Г
Б
Рис. 2. Схема замещения по надежности
Для данной схемы вероятность V№1 определиться как:
V№1 = РГ .РТ .(1-(1- РА)(1- РБ)) = 0.95 .0.985 .(1-(1- 0.96)(1- 0.96)) = 0 .934.
Для энергорайона №2 схема замещения по надежности линейна, поэтому
V№2 = VВ = 0.8.
Вероятность безотказной работы системы в целом определиться в соответствии с теоремой умножения для совместных событий
Vsys = V№1 . V№2 = 0.934 ··0.8 = 0.7472.
Метод статистических испытаний
Для решения данной задачи методом Монте-Карло предполагается использовать датчик случайных чисел v с равномерным распределением в интервале [0..1]. Эти числа сравниваются со значениями VА , VБ, VВ . Сформулируем решающее правило:
если значение случайного числа v не больше вероятности работоспособного состояния каждой из подстанций
v ≤ Vj , , j  { А, Б, В }, (4)
{ А, Б, В }, (4)
то соответствующая подстанция находится в рабочем состоянии, иначе – в обесточенном состоянии.
На этом принципе строятся «испытания» по оценке состояний системы. Если в результате разыгрывания «состояний подстанций» отказов в электроснабжении не будет, то испытание признается положительным, в противном случае – отрицательным. Вероятность безотказной работы системы Usys в этом методе определяется по формуле:
Usys = N+/ N = 1 - N-/ N , (5)
где N – общее число испытаний, N+ - число положительных, N- - число отрицательных испытаний, N = N+ + N- .
Результат каждого испытания удобно представить значением двоичной (бинарной) переменной bj , принимающей значение 1, если выполнен критерий (4) и 0 в ином случае:
если v ≤ Vj то bj = 1 иначе bj = 0.
Из рис. 1 и выражений (4) и (5) следует:
bsys = (bA+bБ)·bВ , (6)
где bsys – состояние системы.
Тогда, после N испытаний, значение N+ можно определить как
N+ 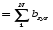
В таблице №1 показана реализация данной методики (подготовлена в Excel) и приведены результаты разыгрывания случайных состояний системы методом Монте-Карло при числе испытаний N = 10.
По данным из таблицы №1 получаем статистическую оценку вероятности работоспособного состояния системы: число значений bsys = 0 равно трем, то есть
N- = 3, N+ = 7, Usys = 7/10 = 0.7.
Абсолютная погрешность этого результата по сравнению с аналитическим методом равна
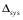 = | Usys - Vsys | = 0.7- 0.7472 = 0.0472. (7)
= | Usys - Vsys | = 0.7- 0.7472 = 0.0472. (7)
Относительная погрешность
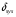 = (
= (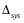 / Vsys ) 100% = 0.0472/0.7472 = 6.3%. (8)
/ Vsys ) 100% = 0.0472/0.7472 = 6.3%. (8)
В соответствии с заданием, увеличим число испытаний вдвое. Для этого достаточно модифицировать данные в Excel – таблице, снова подсчитать число значений bsys = 0 и, сложив с прежним, получим (показан фрагмент таблицы)
N- = 3+2, N+ = 20 – 5 = 15, Usys = 15/20 = 0.75.
Абсолютная погрешность этого результата по сравнению с аналитическим методом равна
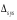 = | Usys - Vsys | = 0.75 - 0.7472 = 0.0028.
= | Usys - Vsys | = 0.75 - 0.7472 = 0.0028.
Относительная погрешность
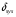 = (
= (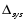 / Vsys ) 100% = 0.0028/0.7472 = 0.4%.
/ Vsys ) 100% = 0.0028/0.7472 = 0.4%.
Дополнительные замечания о методе Монте-Карло
1. Известно, что точность оценки искомых характеристик тем выше, чем больше число испытаний. Для того чтобы выбрать величину N для конкретных испытаний, задаются вероятностью (доверительной) получения правильного решения, обычно принимаемого равной 0.997, что соответствует диапазону ± 3σ для нормального распределения, где σ = √D - с.к.о. исследуемой случайной величины. Тогда необходимое число испытаний определится из формулы
-
δ' =
(9)
где δ' – заданная погрешность определения искомой величины.
Для получения более точного результата число испытаний согласно (9), должно быть равно
N = (0.675· σ / δ' )2
Допустим, мы хотим иметь погрешность на уровне 0.001 (0.1%), т.е. быть уверенными что при решении данной задачи методом статистического моделирования значение Usys будет находится в диапазоне
0.7472 .( 1 ± 0.001) = [0.7464, 0.7479].
Исходя из правила «три сигма», зададим величину σ как крайний возможный случай:
σ = ( 1- Vsys ) / 3 = (1-0.7472)/3 = 0.084.
Тогда требуемое число испытаний будет равно
N = (0.675·0.084/0.001) = 3215.
2. В приведенных выше расчетах принята упрощенная модель статистических испытаний с использованием расчетных вероятностей безотказной работы подстанций, а не отдельных элементов системы, с целью сокращения размерности задачи. Не учитывались также вероятности одновременного отказа нескольких элементов, что необходимо для получения правдоподобных результатов.
3. Датчик случайных чисел с равномерным распределением используется при отсутствии каких-либо сведений о фактическом законе распределения. Достоинство равномерного распределения – простота применения, так как нет необходимости в определении его параметров. Но оценки, полученные в численных экспериментах, оказываются «пессимистическими», если реальный закон существенно отличается от равномерного. Кроме того, датчики случайных чисел с равномерным распределением плохо «работают» при очень малых или очень больших значениях вероятности. Поэтому при выборе модели статистических испытаний большое внимание уделяется обоснованию использования того или иного закона распределения.
Таблица 1
Анализ надежности методом Монте-Карло
Блок
ВБР
V
b
Блок
ВБР
V
b
А
0,898
0,144601
1
А
0,898
0,722673
1
Б
0,898
0,338975
1
Б
0,898
0,580761
1
В
0,8
0,285878
1
В
0,8
0,862889
0
(А+Б)
ИСТИНА
1
(А+Б)
ИСТИНА
1
SYS=(А+Б)*В
1
SYS=(А+Б)*В
0
А
0,898
0,284892
1
А
0,898
0,531509
1
Б
0,898
0,133744
1
Б
0,898
0,157723
1
В
0,8
0,710715
1
В
0,8
0,206039
1
(А+Б)
ИСТИНА
1
(А+Б)
ИСТИНА
1
SYS=(А+Б)*В
1
SYS=(А+Б)*В
1
А
0,898
0,621382
1
А
0,898
0,344317
1
Б
0,898
0,803256
1
Б
0,898
0,752622
1
В
0,8
0,99176
0
В
0,8
0,714726
1
(А+Б)
ИСТИНА
1
(А+Б)
ИСТИНА
1
SYS=(А+Б)*В
0
SYS=(А+Б)*В
1
А
0,898
0,189668
1
А
0,898
0,043997
1
Б
0,898
0,943037
1
Б
0,898
0,305982
1
В
0,8
0,774708
1
В
0,8
0,26292
1
(А+Б)
ИСТИНА
1
(А+Б)
ИСТИНА
1
SYS=(А+Б)*В
1
SYS=(А+Б)*В
1
А
0,898
0,647489
1
А
0,898
0,523631
1
Б
0,898
0,196592
1
Б
0,898
0,788625
1
В
0,8
0,937071
0
В
0,8
0,295981
1
(А+Б)
ИСТИНА
1
(А+Б)
ИСТИНА
1
SYS=(А+Б)*В
0
SYS=(А+Б)*В
1
Фрагменты модифицированной таблицы:
А
0,898
0,126677
1
А
0,898
0,906062
0
Б
0,898
0,305332
1
Б
0,898
0,644128
1
В
0,8
0,878459
0
В
0,8
0,196328
1
(А+Б)
ИСТИНА
1
(А+Б)
ИСТИНА
1
SYS=(А+Б)*В
0
SYS=(А+Б)*В
1
А
0,898
0,308921
1
А
0,898
0,804801
1
Б
0,898
0,823393
1
Б
0,898
0,967697
0
В
0,8
0,749413
1
В
0,8
0,964051
0
(А+Б)
ИСТИНА
1
(А+Б)
ИСТИНА
1
SYS=(А+Б)*В
1
SYS=(А+Б)*В
0
Заключение
В курсовой работе был произведён расчёт показателей надежности простейшей системы электроснабжения двумя вероятностными методами: аналитическим и методом статистических испытаний. Абсолютная погрешность результата, полученного методом Монте-Карло по сравнению с аналитическим методом равна 0.0028. Относительная погрешность составила 0.4%. Также была проведена оценка количества испытаний.
Литература
1. Надежность и диагностика систем электроснабжения железных дорог: учебник для ВУЗов ж\д транспорта / А.В. Ефимов, А.Г. Галкин.- М: УМК МПС России, 2000. - 512с.
2. Китушин В.Г. Надежность энергетических систем: учебное пособие для электроэнергетических специальностей вузов.- М.: Высшая школа, 1984. – 256с.
3. Ковалев Г.Ф. Надежность и диагностика технических систем: задание на контрольную работу №2 с методическими указаниями для студентов IV курса специальности «Электроснабжение железнодорожного транспорта». – Иркутск: ИРИИТ, СЭИ СО РАН, 2000. -15с.
4. Дубицкий М.А. Надежность систем энергоснабжения: методическая разработка с заданием на контрольную работу. – Иркутск: ИрИИТ, ИПИ, СЭИ СО РАН, 1990. -34с.
5. Пышкин А.А. Надежность систем электроснабжения электрических железных дорог. – Екатеринбург: УЭМИИТ, 1993. - 120 с.
6. Шаманов В.И. Надежность систем железнодорожной автоматики и телемеханики: учебное пособие. Иркутск: ИрИИТ, 1999. 223с.
7. Гук Ю.Б. Анализ надежности электроэнергетических установок. - Л.: Энергоатомиздат, Ленинградское отд., 1988. – 224с.
8. Маквардт Г.Г. Применение теории вероятностей и вычислительной техники в системе энергоснабжения.- М.: Транспорт, 1972. - 224с.
9. Надежность систем энергетики. Терминология: сборник рекомендуемых терминов. - М.: Наука, 1964. -Вып. 95. – 44с.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ