Контрольная работа № 1

Задача 1

Рабочие обслуживают три станка, на которых обрабатывается однотипные детали. Вероятность изготовления бракованной детали на первом станке равна 0,2, на втором – 0,3, на третьем – 0,4. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше чем второго, а третьего – в два раза меньше чем второго. Взятая на удачу деталь оказалась бракованной. Найти вероятность того, что она изготовлена на третьем станке.

Решение:

Событие А – взятая деталь оказалась бракованной. Деталь может быть изготовлена на первом, втором или третьем станке, обозначим через В₁, В₂ и В₃. Соответственно Р(В₁) = 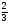, Р(В₂) = 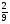, Р(В₃) = .

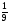Условная вероятность того, что бракованная деталь изготовлена первым станком Р_В1(А) = 0,02, аналогично Р_В2(А) = 0,03 и Р_В3(А) = 0,04.

По формуле полной вероятности

Р(А) =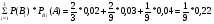

По формуле Бейеса

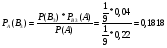
Ответ: Р_А(В₃) = 0,1818

Задача 2

Каждая из пяти упаковок тетрадей содержит две тетради в линейку и три в клетку. Из каждой упаковки случайным образом отбираются по две тетради. Найти вероятность того, что не менее чем в трех из отобранных пяти пар тетрадей обе тетради будут в клетку.

Решение:

Вероятность взять 2 тетради в клетку из пачки

Р = .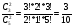

Не менее трех пар из пяти отобранных должны быть – 3 пары, 4 пары, 5 пар.

Вычислим

Р₅(3) + Р₅(4) + Р₅(5).

P_n(k) = ,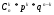

где р = 0,3 и q = 0,7.

Р₅(3) = 0,1323

Р₅(4) = 0,0284

Р₅(5) = 0,0024

Искомая вероятность равна 0,1323 + 0,0284 + 0,0024 = 0,1631

Ответ: 0,1631

Задача 3

Вероятность того, что договор страховой кампании завершится выплатой по страховому случаю, равна 0,1. Страховая кампания заключила 2000 договоров. Найти вероятность того, что страховой случай наступит: а) 210 раз; б) от 190 до 250 раз включительно.

Решение:

а) Используем локальную теорему Лапласа, где k = 210, р = 0,1 и q = 0,9.

P_n(k) = 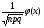, где =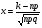

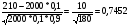
Р₂₀₀₀(210) =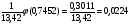

б) Используем интегральную теорему Лапласа, где n = 2000, k₂ = 250, k₁ = 190.

P_n(k₁;k₂) = (x’’) - (x’),

х’’ = .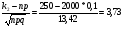

х’ = .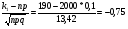

(x’’) = (3,73) = 0,4999.

(x’) = (-0,75) = - 0,2764.

P₂₀₀₀(190;250) = 0,4999 + 0,2764 = 0,7763/

Ответ: а) Р₂₀₀₀(210) = 0,0224, б) Р₂₀₀₀(190;250) = 0,7763

Задача 4

Законное распределение независимых случайных величин Х и У имеют вид:

Х:

x_i

0

1

2

p_i

0,3

?

0,2

Y:

y_i

1

2

p_i

0,4

?

Найти вероятность P(X = 1), P(Y = 2).

Составить закон распределения случайной величины

Z = X*Y.

Проверить выполнение свойства математического ожидания:

M(Z) = M(X)*M(Y)

Решение:

Р(Х = 1) = 1 – (0,3 + 0,2) = 0,5

Р(Y = 2) = 1 – 0,4 = 0,6

Составим закон распределения случайной величины Z = X*Y

x_j

0

1

2

y_i

p_j

p_i

0,3

0,5

0,2

1

0,4

0

0,12

1

0,2

2

0,08

2

0,6

0

0,18

20,3

4

0,12

z_i

0

1

2

4

p_i

0,3

0,2

0,38

0,12

p_i = 0,3 + 0,2 + 0,38 + 0,12 = 1

M(Z) = 0*0,3 + 1*0,2 + 2*0,38 + 4*0,12 = 1,44

M(X) = 0*0,3 + 1*0,5 + 2*0,2 = 0,9

M(Y) = 1*0,4 + 2*0,6 = 1,6

M(Z) = M(X)*M(Y) = 0,9*1,6 = 1,44.

Ответ:

Z_i

0

1

2

4

P_i

0,3

0,2

0,38

0,12

Задача 5

Функции распределения непрерывной случайной величины Х имеет вид:

0 при х  -1,

F(x) = (х + 1)² при -1  х  0,

1 при х  0.

Найти математическое ожидание этой случайной величины и вероятность того, что при каждом из трех независимых наблюдений этой случайной величины будет выполнено условие .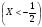

Решение:

Найдем плотность распределения

0 при х  -1,

f(x) = F’(x) = 2(x + 1) при -1  х  0,

1 при х  0.

М(х) =

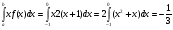
- математическое ожидание.

Р(х 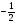 ) = Р( -1  х < 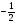) = F(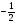) – F( -1) =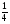

Ответ: М(х) = 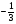и Р(х < ) =

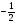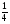
Контрольная работа № 4

Задача 1

При выборочном опросе ста телезрителей, пользующихся услугами спутникового телевидения, получены следующие результаты распределения их по возрасту

Возраст (лет)

Менее 20

20 – 30

30 – 40

40 – 50

50 – 60

60 – 70

Более 70

Итого

Количество пользователей (чел.)

8

17

31

40

32

15

7

150

Найти:

а) Вероятность того, что средний возраст телезрителей отличается от среднего возраста, полученного по выборке, не более чем на два года (по абсолютной величине);

б) Границы, в которых с вероятностью 0,97 заключена доля телезрителей, возраст которых составляет от 30 до 50 лет;

в) Объем бесповторной выборки, при котором те же границы для доли можно гарантировать с вероятностью 0,9876; дать ответ на тот же вопрос, если никаких предварительных сведений о доле нет.

Решение:

Вычислим среднюю арифметическую и дисперсию распределения. Величина интервала k = 10 и с = 45, середина пятого интервала. Вычислим новые варианты в рабочей таблице:

i

[x_i;x_i+1]

x_i

u_i

n_i

u_i;n_i

u²_i;n_i

u_i +1

(u_i + 1)n_i

1

10 – 20

15

-3

8

-24

72

-2

32

2

20 – 30

25

-2

17

-34

68

-1

17

3

30 – 40

35

-1

31

-31

31

0

0

4

40 – 50

45

0

40

0

0

1

40

5

50 – 60

55

1

32

32

32

2

128

6

60 – 70

65

2

15

30

60

3

135

7

70 – 80

75

3

7

21

63

4

112



315

0

150

-6

326

7

464

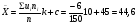
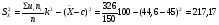
a) Найдем среднюю квадратическую ошибку бесповторной выборки

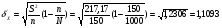
Искомая доверительная вероятность

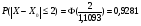
б) Выборочная доля зрителей от 30 до 50 лет

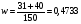
Средняя квадратическая ошибка бесповторной выборки для доли

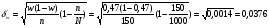
Из соотношения  = Ф(t) = 0,97; t = 2,17

Предельная ошибка выборки для доли  = 2,17*0,0376 = 0,08156

Искомый доверительный интервал

0,4733 – 0,08156  р  0,4733 + 0,08156

0,3918  р  0,5549

в) Учитывая  = Ф(t) = 0,3876; t = 2,5

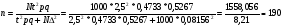человек.

Если о доле p = w ничего не известно, полагаем (pq)_max = 0,25

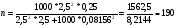человек.

Ответ: а) 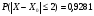; б) 0,3918  р  0,5549 ; в) 190 человек

Задача 2

По данным задачи 1, используя критерий ² – Пирсона, при уровне значимости, а = 0,5 проверить гипотезу о том, что случайная величина Х – количество телезрителей – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.

Решение:

Выдвигается гипотеза Н₀: случайная величина Х – количество телезрителей – распределена нормально. с параметрами а = 44,6 и ² = 217,17.

Для расчета р_i используем функцию Лапласа

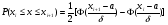
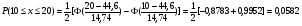
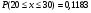
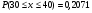
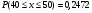
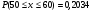
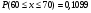
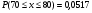
Дальнейшие расчеты покажем в таблице

i

[x_i;x_i+1]

n_i

p_i

np_i

(n_i – np_i)

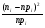
1

10 – 20

8

0,0582

8,7225

0,522

0,0598

2

20 – 30

17

0,1183

17,738

0,5439

0,0307

3

30 – 40

31

0,2071

31,065

0,0042

0,0001

4

40 – 50

40

0,2472

37,073

8,5703

0,2312

5

50 – 60

32

0,2034

30,51

2,2201

0,0728

6

60 – 70

15

0,1099

16,478

2,183

0,1325

7

70 – 80

7

0,0517

7,755

0,57

0,0735



150

0,9956

149,34

0,6006

Фактическое значение ² = 0,6006 Соотносим критическое значение ²_0,05;4 = 9,49 k = m – r – 1 = 7 – 2 – 1 = 4.

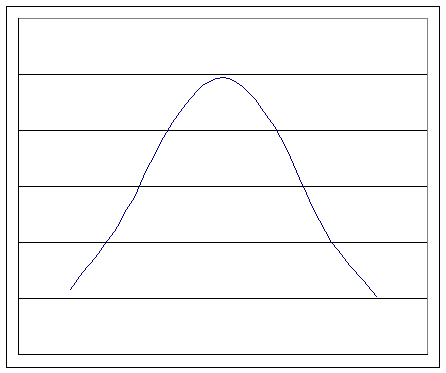
Так как ²  ²_0,05;4, гипотеза Н₀ согласуется с опытными данными. Выполним построение:

Ответ: Гипотеза о выбранном теоретическом нормальном законе N (44,6; 217,17) согласуется с опытными данными.

Задача 3

Распределение 50 однотипных малых предприятий по основным фондам Х (млн., руб.) и себестоимости выпуска единицы продукции. У (тыс., руб.) представлено в таблице:

у

х

1,25

1,5

1,75

2,0

2,25

Итого

80 – 130

1

2

3

6

130 – 180

1

4

3

8

180 – 230

4

8

3

1

16

230 – 280

2

5

4

11

280 – 330

3

4

2

9

Итого:

5

3

16

9

7

50

Необходимо:

1. Вычислить групповые средние x_j и y_i и построить эмпирические линии регрессии.

2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:

а) найти уравнение прямых регрессий и построить их графики на одном чертеже с эмпирическими линиями регрессии;

б) вычислить коэффициент корреляции на уровне значимости, а=0,05, оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;

в) используя соответствующие уравнения регрессии, определить количество выпускаемой продукции при стоимости одной единицы продукции, равной 2,5 тыс., руб.

Решение:

1) Составим корреляционную таблицу

х

у

x_i

1,25

1,5

1,75

2

2,25

n_i

у_i

80 – 130

105

1

2

3

6

2,0833

130 – 180

155

1

4

3

8

2,0625

180 – 230

205

4

8

3

1

16

1,7656

230 – 280

255

2

5

4

11

1,5456

280 – 330

305

3

4

2

9

1,4722

n_j

5

13

16

9

7

50

x_j

285

255

220,63

160,56

140,71

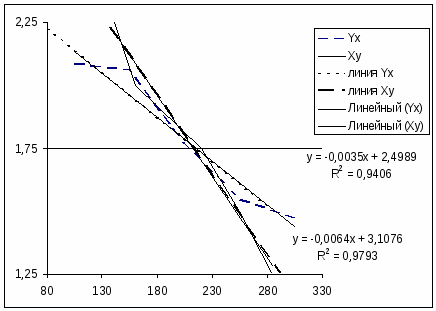
Построим эмпирические линии регрессии

2) Предположим, что между переменными Х и Y существует линейная корреляционная зависимость;

а) Вычислим среднее значение

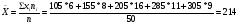
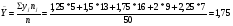
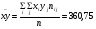
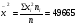
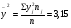
Найдем уравнение

у_х = b_yx(x – x) + y,

где b_yx =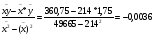

у_х = - 0,0036(х – 214) + 1,75

у_х = - 0,0036х + 2,5105

х_у - х = b_yx(у – у),

где b_ху =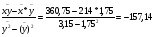

х_у = - 157,14(х – 1,75) + 214

х_у = - 157,14х + 489

б) Коэффициент корреляции

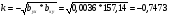
связь обратная и тесная;

Статистика критерия

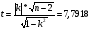
При а = 0,05 и k = 48; t_0,05;48 = 2,01, так как t  t_0,05;48 коэффициент значительно отличается от 0.

в) Используя х_у = - 157,14у + 489

х = - 157,14*2,5 + 489 = 96,14

Ответ: а) у_х = - 0,0036х + 2,5105; х_у = - 157,14х + 489.

б) k = - 0,7473.

в) х = 96,14 при у = 2,5