Расширения полей












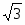
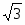
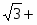
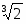
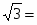
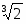
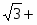
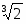
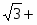
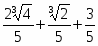
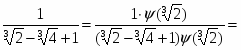
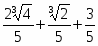
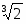
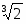
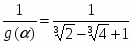 Содержание
Содержание
Введение
1. Простое алгебраическое расширение поля.
4
1.1. Простое расширение поля.
4
1.2. Минимальный полином алгебраического элемента.
5
1.3. Строение простого алгебраического расширения поля.
6
1.4. Освобождение от алгебраической иррациональности в знаменателе дроби.
6
2.Составное алгебраическое расширение поля.
8
2.1. Конечное расширение поля.
8
2.2. Составное алгебраическое расширение поля.
8
2.3. Простота составного алгебраического расширения поля.
10
2.4. Поле алгебраических чисел.
11
2.5. Алгебраическая замкнутость поля алгебраических чисел.
12
3. Сепарабельные и несепарабельные расширения.
12
4. Бесконечные расширения полей.
17
4.1. Алгебраически замкнутые поля.
17
4.2. Простые трансцендентные расширения.
22
Заключение
26
Литература
27
Введение.
В педагогических вузах введена программа единого курса алгебры и теории чисел. Главная цель этого курса—изучение основных алгебраических систем и воспитание алгебраической культуры, необходимой будущему учителю для глубокого понимания целей и задач как основного школьного курса математики, так и школьных факультативных курсов.
На наш взгляд, наиболее целесообразным является введение в школьное преподавание элементов современной абстрактной алгебры.
Начавшийся в ХХ веке процесс алгебраизации математики не прекращается, а это вызывает упорные попытки введения в школьное математическое образование основных алгебраических понятий.
Математическая глубина и необычайно широкая сфера применения полей сочетаются с простотой ее основных положений – понятий полей, целый ряд важных теорем можно сформулировать и доказать, обладая начальными представлениями в области теории множеств. Поэтому теория полей как нельзя лучше подходит для того, чтобы показать школьникам образец современной математики.
Кроме того, изучение элементов теории поля полезно для школьников, способствует их интеллектуальному росту, проявляющемуся в развитии и обогащении различных сторон их мышления, качеств и черт личности, а также воспитанию у учащихся интереса к математике, к науке.
Простое алгебраическое расширение поля.
1.1.Простое расширение поля.
Пусть P[x] — кольцо полиномов от x над полем P, где P — подполе поля F. Напомним, что элемент поля F называется алгеб раическим над полем P, если является корнем какого-нибудь полинома положительной степени из P [x].
Определение. Пусть P < F и F. Простым расширением поля P с помощью элемента a называется наименьшее подполе поля F, содержащее множество Р и элемент a. Простое расширение P с помощью a обозна чается через P (a), основное множество поля P (a) обо значается через Р(a).
Пусть aF, P [x] — кольцо полиномов от x и
P[x]={f(a)fP[x]},
т. е. P [a] есть множество всех выражений вида a0 + a1a+...+ anan, где а0, a1,...anP и n — любое натураль ное число.
Легко видеть, что алгебра P[a], +, —, ., 1 — подкольцо поля P (a) — является кольцом; это кольцо обозначается символом P [a].
Теорема 1.1. Пусть P [x]— кольцо полиномов от х над P и P (a)— простое расширение поля P. Пусть — отображение P[x] на P[] такое, что (f)=f() для любого f из P[x]. Тогда:
(а) для любого а из Р (а) = а;
(b) (x) = ;
(с) является гомоморфизмом кольца P [x] на кольцо P [a];
(d) Ker ={fP[x]f()=0};
(е) фактор-кольцо P [x]/Кег изоморфно кольцу P [].
Доказательство. Утверждения (а) и (Ь) непосредственно следуют из определения . Отображение сохраняет главные операции кольца P [x], так как для любых f и g из P[x]
(f + g)=f()+g(), (fg)= f()g(), (1)=1.
Далее, по условию, есть отображение Р[х] на Р[]. Сле довательно, является гомоморфизмом кольца P [x] на кольцо P [].
Утверждение (d) непосредственно следует из определе ния отображения .
Поскольку — гомоморфизм кольца P [x] на P [], то фактор-кольцо P[x]/Кег y изоморфно кольцу P [a].
Следствие 1.2. Пусть a — трансцендентный элемент над полем P. Тогда кольцо полиномов P [x] изоморфно кольцу P [a].
Доказательство. В силу трансцендентности a над P Kery={0}. Поэтому P[x]/{0} P [a]. Кроме того, фактор-кольцо кольца P [x] по нулевому идеалу изоморфно P [x]. Следовательно, P [x] P [a].
1.2.Минимальный полином алгебраического элемента.
Пусть P [x] — кольцо полиномов над полем P.
Определение. Пусть a — алгебраический элемент над полем P. Минимальным полиномом элемента a, над P называется нормированный полином из P[x] наименьшей степени, корнем которого является a. Степень минимального полинома называется степенью элемента a над P.
Легко видеть, что для всякого элемента a, алгебраического над P , существует минимальный полином.
Предложение 1.3. Если а — алгебраический элемент над полем P, а g и — его минимальные полиномы над P, то g=.
Доказательство. Степени минимальных полиномов g и совпадают. Если g , то элемент a (степени n над P) будет корнем полинома g - , степень которого меньше степени полинома (меньше n), что невозможно. Следовательно, g=.
Теорема 1.4. Пусть a — алгебраический элемент степени n над полем P (aP) и g — его минимальный полином над P. Тогда:
(а) полином g неприводим в кольце P [x];
(b) если f (a) = 0, где f P[x], то g делит f;
(с) фактор-кольцо P [x]/(g) изоморфно кольцу P [a];
(d) P [x]/(g) является полем;
(е) кольцо P [a] совпадает с полем P (a).
Доказательство. Допустим, что полином g приводим в кольце P [x], т. е. существуют в P[x] такие поли номы и h, что
g = h, 1deg , deg h
Тогда g(a) = (a)h(a) = 0. Так как P (a) — поле, то ( a) = О или h(a) = 0, что невозможно, поскольку, по условию, степень элемента a над P равна п.
Предположим, что f P[x] и f(a) = 0. По условию, g(a) = 0. Следовательно, f и g не могут быть взаимно про стыми. Поскольку полином g неприводим, то g делит f.
Пусть — гомоморфизм кольца P [x] на кольцо P [a] ((f)=f(a) для всякого f из P[x]), рассмотренный в тео реме 2.1. В силу (Ь) ядро гомоморфизма состоит из крат ных полинома g, т.е. Кег = (g). Следовательно, фактор-кольцо P = P [x]/(g) изоморфно кольцу P [a].
Поскольку P[a]P(a), то P [a] есть область целост ности. Так как P P[a], то фактор-кольцо P также есть область целостности. Нам надо показать, что любой ненулевой элемент f из P обратим в P. Пусть f — элемент смежного класса f. Так как f 0, то f(a)0; поэтому полином g не делит полином f. Поскольку полином g неприводим, отсюда следует, что полиномы f и g — взаимно простые. Следовательно, в Р[x] существуют такие полиномы u и v, что uf + vg=1. Отсюда вытекает равенство uf = 1, показывающее, что элемент f обратим в кольце P. Итак, установлено, что фактор-кольцо P является полем.
В силу (с) и (d) P [a] является полем и поэтому P(a)P[a]. Кроме того, очевидно, P[a]P(a). Значит, P[a] = P(a). Следовательно, кольцо P [a] совпадает с полем P (a).
1.3.Строение простого алгебраического расширения поля.
Теорема 1.5. Пусть a — алгебраический над полем P элемент положительной степени n. Тогда любой элемент поля P(a) однозначно представим в виде линейной комби нации n элементов 1, a, ..., an-1 с коэффициентами из Р.
Доказательство. Пусть — любой элемент поля P (a). По теореме 1.4, P(a) = P[a]; следовательно, существует в P[x] полином f такой, что
(1) = f(a).
Пусть g — минимальный полином для a над P; в силу условия теоремы его степень равна п. По теореме о делении с остатком, существуют в P[x] полиномы h и r такие, что
(2) f = gh + r, где r = 0 или der r < der g = n , т. е. r=c0+c1x +…cn-1xn-1 (ciP). Полагая в (2) x = а и учитывая равенство (1), имеем
(3) = c0+c1a +…cn-1an-1
Покажем, что элемент однозначно представим в виде линейной комбинации элементов 1, a, ..., an-1. Пусть
(4) = d0+d1a +…dn-1an-1 (di P)
—любое такое представление. Рассмотрим полином
= (с0 – d0) + (c1 - di.)x + . . . + (сn-1 –dn-1)xn-1
Случай, когда степень меньше n, невозможен, так как в силу (3) и (4) (a) = 0 и степень меньше степени g. Возможен лишь случай, когда = 0, т. е. с0 = d0, . . . , сn-1 = dп-1. Следовательно, элемент однозначно представим в виде линейной комбинации элементов 1, a,…,an-1.
1.4.Освобождение от алгебраической иррациональности в знаменателе дроби.
Задача об освобождении от алгебраической иррациональности в знаменателе дроби состоит в следующем. Пусть a — алгебраический элемент степени n>1 над полем P; f и h — полиномы из кольца полино мов P [x]и h(a) 0. Требуется представить элемент f(a)/h(a)0P(a) в виде линейной комбинации степеней эле мента a, т. е. в виде (a),
где 0P[x].
Эта задача решается следующим образом. Пусть g — минимальный полином для a над P. Так как, по теореме 1.4, полином неприводим над P и h(a) 0, то g не делит h и, значит, полиномы h и g — взаимно простые. Поэтому существуют в P[x] такие полиномы u и v, что
uh+vg=1 (1)
Поскольку g(a) = 0, из (1) следует, что
u(a)g(a) = 1, 1/h(a) = u(a).
Следовательно, f(a)/h(a) = f(a)u(a), причем f,u 0P[x] и f(a)u(a)0P[a]. Итак, мы освободились от иррациональности в знаменателе дроби f(a)/h(a) .
Пример.
Освободиться от иррациональности в знаменателе дроби
.
Решение. В нашем случае =. Минимальным многочленом этого числа является
p(x)=x3-2.
Многочлены p(x) и g(x)=-x2+x+1 взаимно просты. Поэтому существуют такие многочлены и , что
p+g=1.
Для отыскания и применим алгоритм Евклида к многочленам p и g:
-x3-2 -x2+x+1 -x2+x+1 2x-1
x3-x2-x -x-1 -x2+1/2x -1/2x+1/4
x2+x-2 1/2x+1
x2-x-1 1/2x-1/4
2x-1 5/4
Таким образом,
p=g(-x-1)+(2x-1),
g=(2x-1)(-1/2x+1/4)+5/4.
Откуда находим
(2x-1)=p+g(x+1),
5/4=g-(p+g(x+1))(-1/2x+1/4)
или
p1/5(2x-1)+g(4/5+1/5(2x2+x-1))=1,
p1/5(2x-1)+g(2/5x2+1/5x+3/5)=1.
Таким образом,
(x)= (2/5x2+1/5x+3/5).
Тогда
y()=y()=.
Следовательно
.
2.Составное алгебраическое расширение поля.
2.1. Конечное расширение поля.
Пусть P — подполе поля F. Тогда мы можем рассматривать F как векторное пространство над P, т. е. рассматривать векторное пространство F, +, { 0P},
где - операция умножения элементов из F на скаляр 0P.
Определение. Расширение F поля P называется конечным, если F, как векторное пространство над P, имеет конечную размерность. Эта размерность обозначается через [F : P].
Предложение 2.1. Если a — алгебраический элемент степени n над P, то [P (a):P]=n.
Это предложение непосредственно следует из теоремы 1.5.
Определение. Расширение F поля P называется алгебраическим, если каждый элемент из F является алгебра ическим над P.
Теорема 2.2. Любое конечное расширение F поля P является алгебраическим над P.
Доказательство. Пусть n-размерность F над P. Теорема, очевидно, верна, если n = 0. Предположим, что n>0. Любые n+1 элементов из F линейно зависимы над P. В частности, линейно зависима система элементов 1, a, ..., an, т. е. существуют в P такие элементы с0, с1,…,cn не все равные нулю, что с01+ с1a+…+cn an = 0.
Следовательно, элемент a является алгебраическим над P.
Отметим, что существуют алгебраические расширения поля, не являющиеся конечными расширениями.
2.2. Составное алгебраическое расширение поля.
Расширение F поля P называется составным, если существует
возрастающая цепочка подполей L i поля F такая, что
P = L0 L1 … Lk= F и k>1.
Теорема 2.3. Пусть F — конечное расширение поля L и L — конечное расширение поля P. Тогда F является конечным расширением поля P и
[F : P] = [F : L][ L : P].
Доказательство. Пусть
(1) a1,…,am — базис поля L над P (как векторного пространства) и
(2) 1,…,n — базис поля F над L . Любой элемент d из F можно линейно выразить через базис:
(3) d = l11+...+lnn (lk 0L).
Коэффициенты 1k можно линейно выразить через базис (1):
(4) lk = p1k a +…+ pmk am (pik0P).
Подставляя выражения для коэффициентов lk в (3), получаем
d = pik aik.
i0{1,…,m}
k0{1,…,n}
Таким образом, каждый элемент поля F представим в виде линейной комбинации элементов множества B, где
B = { a ik{1,..., m}, k 0 {l,..., n}}.
Отметим, что множество B состоит из nm элементов.
Покажем, что B есть базис F над полем P. Нам надо показать, что система элементов множества B линейно независима. Пусть
(5) cikaik = 0,
I,k
где cik 0 P. Так как система (2) линейно независима над L , то из (5) следуют равенства
(6) с1ka 1+...+сmka m = 0 (k = 1,..., n).
Поскольку элементы a 1, ..., a m линейно независимы над P, то из (6) следуют равенства
c1k = 0,…,cmk = 0 (k = 1, ..., n),
показывающие, что все коэффициенты в (5) равны нулю. Таким образом, система элементов B линейно независима и является базисом F над P.
Итак установлено, что [F , P] = nm = [F: L][L: P]. Следовательно, F является конечным расширением поля P и имеет место формула (I).
Определение. Расширение F поля P называется составным алгебраическим, если существует возрастающая цепочка подполей поля P
P = L0 � L1 �…� Lk= F и k>1 (1)
такая, что при i = 1,..., k поле L i является простым алгебраическим расширением поля L i-1. Число k назы вается длиной цепочки (1).
Следствие 2.4. Составное алгебраическое расшире ние F поля P является конечным расширением поля P.
Доказательство легко проводится индукцией по длине цепочки (1) на основании теоремы 2.3.
Теорема 2.5. Пусть 1,..., k — алгебраические над полем P элементы поля F . Тогда поле P(1,..., k) является конечным расширением поля P.
Доказательство. Пусть
L 0 = P, L 1 = P [1], L 2= P [1, 2,],..., L k = P [1 ,..., k].
Тогда L1 = P [1] есть простое алгебраическое расшире ние поля L0; L2 есть простое алгебраическое расширение поля L1 , так как
L2 = P [1,2] = (P [1])[2] = L1[a2] = L1(a2) и т. д.
Таким образом,
P = L0 � L1 �…� Lk= F
где Li = Li-1(ai ) при i = 1, ..., k, т. е. каждый член цепочки (2) является простым алгебраическим расширением предшествующего члена цепочки. Итак, поле F является составным алгебраическим расширением поля P. Следовательно, в силу следствия 2.4 поле F является конеч ным расширением поля P .
Следствие 2.6. Составное алгебраическое расшире ние поля является алгебраическим расширением этого поля.
2.3. Простота составного алгебраического расширения поля.
Теорема 2.7. Пусть числовое поле F есть составное алгебраическое расширение поля P . Тогда F является простым алгебраическим расширением поля P.
Доказательство. Пусть P �L � F , причем L = P(), F = L() и, следовательно, F = P(, ).
Пусть f и g — минимальные полиномы над P соответственно для чисел и и deg f = m, deg g = n. Полиномы f и g неприводимы над P и, следовательно, не имеют в поле E комплексных чисел кратных корней. Пусть
= 1 ,..., m — корни полинома f в C и
= 1 ,..., n — корни полинома g в C.
Рассмотрим конечное множество М:
M = {(i-)/(-k)i{1,…,m}, k{2,…,n}}.
Поскольку P — числовое множество (и, значит, бесконеч ное), то в P существует число c, отличное от элементов множества М, cPМ, cМ. Пусть
(1) = + c.
Тогда выполняются соотношения
(2) i +ck = (i{1,..., m}, k{2, ..., n}).
В самом деле, в случае равенства +с = i+сk было бы
с = (i-)/(-k) M
что противоречило бы выбору числа c.
Пусть F1 = P () и F1 — кольцо полиномов от x. Пусть h = f( - cx) — полином из F1[x] (, cP() = F1). Покажем, что x- есть наибольший общий делитель полиномов h и g в кольце F1[x]. Так как g() = 0, то x- делит g в E[x]. Далее, в силу (1)
h() = f(-c) = f() = 0.
Поэтому x- делит полином h в E[x]. Таким образом, x- есть общий делитель h и g в кольце E[x].
Докажем, что g и h в С не имеет корней, отличных от . В самом деле, допустим, что k, k{2 ,..., n}, есть их общий корень. Тогда h(k) = f( - сk) = 0. Сле довательно, найдется такой индекс i{1 ,..., m}, что = ai+cbk (k>1), а это противоречит (2). На основании этого заключаем, что x- есть наибольший общий дели тель g и h в E[x]. Поскольку x - — нормированный полином, то отсюда следует, что x - является наиболь шим общим делителем g и h в кольце F1[x]. Поэтому
(x-) F1[x] и F1 = P().
Кроме того, = - c F1. Таким образом,
F = P(, ) F1, F1F.
Следовательно, F = P(). Далее, так как (как и всякий элемент из F) есть алгебраический элемент над P и F = P (), то поле F = P () является искомым простым алгебраическим расширением поля P.
2.4. Поле алгебраических чисел.
В классе подполей поля комплексных чисел одним из наиболее важных является поле алгебраических чисел.
Определение. Алгебраическим числом называется комплексное число, являющееся корнем полинома поло жительной степени с рациональными коэффициентами.
Отметим, что алгебраическое число есть любое комплексное число, алгебраическое над полем Q. В частности, любое рациональное число является алгебраическим.
Теорема 2.8. Множество A всех алгебраических чисел замкнуто в кольце E = С, +, —, •, 1 комплексных чисел. Алгебра A = А, +, —, •, 1 является полем, подполем поля E.
Доказательство. Пусть a и b — любые элементы из А. По следствию 2.6, поле Q(a, b) является алгебраическим над Q. Поэтому числа a+b, -а, ab, 1 являются алгебраическими, т. е. принадлежат множеству A. Таким образом, множество А замкнуто относительно главных операций кольца E. Поэтому алгебра A — подкольцо кольца E — является кольцом.
Кроме того, если a —ненулевой элемент из А, то a-1 Q (a, b) и поэтому а-1 принадлежит А. Следовательно, алгебра A есть поле, подполе поля E.
Определение. Поле A = А, +, —, •, 1 назы вается полем алгебраических чисел.
Пример.
Показать, что число = является алгебраическим.
Решение. Из = следует -.
Возведем обе части последнего равенства в третью степень:
3-329-3=2
или
3 +9-2=3(a2+1).
Теперь обе части равенства возводим во вторую степень:
a6+18a4+81a2-4a3-36a+4=27a4+54a2+27
или
a6-9a4-4a3+27a2-36a-23=0.
Таким образом a является корнем многочлена
f(x)= a6-9a4-4a3+27a2-36a-23=0
с рациональными коэффициентами. Это значит что a — алгебраическое число.
2.5. Алгебраическая замкнутость поля алгебраических чисел.
Теорема 2.9. Поле алгебраических чисел алгебраически замкнуто.
Доказательство. Пусть A [x] — кольцо полиномов от x над полем A алгебраических чисел. Пусть
f = а0 + а1x+... + аnхn (а0 ,…, аn A)
— любой полином положительной степени из A[x]. Нам надо доказать, что f имеет корень в А. Так как fC[x] и поле E алгебраически замкнуто, то f имеет корень в E т. е. существует такое комплексное число с, что f(с) = 0. Пусть L= Q(а0, ..., аn) и L (с) — простое алгебраическое расширение поля L с помощью с. Тогда Q �L � L (c) есть конечное алгебраическое расширение поля L. По теореме 2.2, L есть конечное расширение поля Q. В силу теоремы 2.3 L (с) является конечным расширением поля Q. Отсюда, по теореме 2.2, следует, что поле L (с) является алгебраическим расширением поля Q и, значит, cA. Таким образом, любой полином из A[x] положительной степени имеет в A корень, т. е. поле A алгебраически замкнуто.
3. Сепарабельные и несепарабельные расширения.
Пусть — поле.
Выясним, может ли неразложимый в [x] многочлен обладать кратными корнями?
Для того чтобы f(x) обладал кратными корнями, многочлены f(x) и f(x) должны иметь общий отличный от константы множитель, который можно вычислить уже в [x]. Если многочлен f(x) неразложим, то ни с каким многочленом меньшей степени f(x) не может иметь непостоянных общих множителей, следовательно, должно иметь место равенство f '(x) = 0.
Положим
n n
f(x) =ax f(x) =ax-1
0 1
Так как f(x) = О, в нуль должен обращаться каждый коэффициент:
a = 0 ( = l, 2, ..., n).
В случае характеристики нуль отсюда следует, что a = 0 для всех 0. Следовательно, непостоянный многочлен не может иметь кратных корней. В случае же характеристики p равенства a = 0 возможны и для 0, но тогда обязаны выполняться сравнения
0(p).
Таким образом, чтобы многочлен f(x) обладал кратными корнями, все его слагаемые должны обращаться в нуль, за исключением тех ax, для которых 0(p), т. е. f(x) должен иметь вид
f(x) = a0+apxp+a2px2p+…
Обратно: если f(x) имеет такой вид, то f(x)=0.
В этом случае мы можем записать:
f(x) = (xp).
Тем самым доказано утверждение: В случае характеристики нуль неразложимый в [x] многочлен f (x) имеет только простые корни, в случае оке характеристики p многочлен f(x) (если он отличен от константы) имеет кратные корни тогда и только тогда, когда его можно представить как многочлен от xp.
В последнем случае может оказаться, что (x) в свою очередь является многочленом от xp. Тогда f(x) является многочленом от xp2. Пусть f(x) — многочлен от xpe
f(x) = ( xpe),
но не является многочленом от xpe+1. Разумеется, многочлен (у) неразложим. Далее, (у) 0, потому что иначе (у) имел бы вид (ур) и, следовательно, f(x) представлялся бы в виде (хpе+1), что противоречит предположению. Следовательно, (у) имеет только простые корни.
Разложим многочлен (у) в некотором расширении основного поля на линейные множители: m
(y) = (y-i).
1
Тогда
m
f(x) = ( xpe -i)
1
Пусть i— какой-нибудь корень многочлена xpe -i. Тогда xipe = i,
xpe -i = xpe – ipe = (x-i) pe.
Следовательно, i является ре-кратным корнем многочлена xpe -i и
m
f(x) = ( x -i) ре.
1
Все корни многочлена f(x) имеют, таким образом, одну и ту же кратность ре.
Степень m многочлена называется редуцированной степенью многочлена f(x) (или корня i); число e называется показателем многочлена f (x) (или корня i) над полем . Между степенью, редуцированной степенью и показателем имеет место соотношение
n = m ре,
где m равно числу различных корней многочлена f(x).
Если — корень неразложимого в кольце [x] многочлена, обла дающего лишь простыми корнями, то называется сепарабельным элементом над или элементом первого рода над 1). При этом неразложимый многочлен, все корни которого сепарабельны, назы вается сепарабельным. В противном случае алгебраический эле мент и неразложимый многочлен f(x) называются несепарабельными или элементом (соответственно, многочленом) второго рода. Наконец, алгебраическое расширение , все элементы которого сепарабельны над , называется сепарабельным над , а любое другое алгебраическое расширение называется несепарабельным.
В случае характеристики нуль согласно сказанному выше каждый неразложимый многочлен (а потому и каждое алгебраи ческое расширение) является сепарабельным. Позднее мы увидим, что большинство наиболее важных и интересных расширений полей сепарабельны и что существуют целые классы полей, вообще не имеющих несепарабельных расширений (так называемые «совер шенные поля»). По этой причине в дальнейшем все связанное специально с несепарабельными расширениями набрано мелким шрифтом.
Рассмотрим теперь алгебраическое расширение = (). Когда степень n уравнения f(x) = 0, определяющего это расширение, равна степени ( : ), редуцированная степень m оказывается равной числу изоморфизмов поля в следующем смысле: рассмот рим лишь такие изоморфизмы ', при которых элементы подполя остаются неподвижными и, следовательно, перево дится в эквивалентное поле ' (изоморфизмы поля над полем ) и при которых поле-образ ' лежит вместе с полем внутри некоторого общего для них поля . В этих условиях имеет место теорема:
При подходящем выборе поля расширение =() имеет ровно m изоморфизмов над и при любом выборе поля поле не может иметь более m таких изоморфизмов.
Доказательство. Каждый изоморфизм над должен пере водить элемент в сопряженный с ним элемент ' из . Выбе рем так, чтобы f(x) разлагался над на линейные множители; тогда окажется, что элемент имеет ровно m сопряженных эле ментов ,', ... При этом, как бы ни выбиралось поле , элемент не будет иметь в нем более m сопряженных. Заметим теперь, что каждый изоморфизм ()(') над полностью определяется заданием соответствия '. Действительно, если переходит в ' и все элементы из остаются на месте, то элемент
akk (ak)
должен переходить в
akk
а этим определяется изоморфизм.
В частности, если — сепарабельный элемент, то m = n и, следо вательно, число изоморфизмов над основным полем равно степени расширения.
Если имеется какое-то фиксированное поле, содержащее все рассматриваемые поля, в котором содержатся все корни каждого уравнения f(x) = 0 (как, например, в поле комплексных чисел), то в качестве можно раз и навсегда взять это поле и поэтому отбросить добавление «внутри некоторого » во всех предложе ниях об изоморфизмах. Так всегда поступают в теории числовых полей. Позднее мы увидим, что и для абстрактных полей можно построить такое поле .
Обобщением приведенной выше теоремы служит следующее утверждение:
Если расширение получается из последовательным присоединением m
алгебраических элементов 1, ..., m, причем каждое из i,- является корнем
неразложимого над (1, ..., i-1) уравнения редуцированной степени n'i, то
m
расширение имеет ровно ni изоморфизмов над и ни в одном
1
расширении нет большего числа таких изоморфизмов поля .
Доказательство. Для m = 1 теорема уже была доказана выше. Предположим ее справедливой для расширения 1 = (1, ..., m-1): в некотором подходящем расширении
m-1
1 есть ровно ni изоморфизмов поля над .
1 m-1
Пусть 11— один из этих ni изоморфизмов. Утверждается, что в подходящим образом выбранном поле он может быть продолжен до изоморфизма = 1 (m) = (m) не более чем nm способами.
Элемент m удовлетворяет некоторому уравнению f1(x) = 0 над 1 с nm раз личными корнями. С помощью изоморфизма 11многочлен f1(x) перево дится в некоторый многочлен f1(x). Но тогда f1(x) в подходящем расширении имеет опять-таки n¢m различных корней и не больше. Пусть am— один из этих корней. В силу выбора элемента am изоморфизм S1S1 продолжается до изоморфизма (am) (am) с amam одним и только одним способом: действительно, это продолжение задается формулой
ckmk ckmk
Так как выбор элемента m может быть осуществлен n'm способами, существует n'm продолжений такого сорта для выбранного изоморфизма 11
Так как в свою очередь этот изоморфизм может быть выбран
m-1
n'i способами,
1
то всего существует (в том поле , в котором содержатся все корни всех рассматриваемых уравнений)
m-1 m
n'in'm = n'i
1 1
изоморфизмов расширения над полем , что и требовалось доказать.
Если ni — полная (нередуцированная) степень элемента i над (1,...,i-1), то ni равно степени расширения (1, ... , i) поля (1, ... , i-1);
следовательно, степень ( : ) равна
m
n'i .
1
Если сравнить это число с числом изоморфизмов
m
n'i .
1
то получится следующее предложение:
Число изоморфизмов расширения = (1, ... , m) над (в некотором подходящем расширении ) равно степени ( : ) тогда и только тогда, когда каждый элемент i сепарабелен над полем (1, ... , i-1). Если же хотя бы один элемент i несепарабелен над соответствующим полем, то число изоморфизмов меньше степени расширения.
Из этой теоремы сразу получается несколько важных следствий. Прежде всего теорема утверждает, что свойство каждого элемента i быть сепарабельным над предыдущим полем есть свойство самого расширения независимо от выбора порождающих элементов i. Так как произвольный элемент поля может быть взят в качестве первого порождающего, элемент оказывается сепарабельным, если все i являются таковыми. Итак:
Если к полю последовательно присоединяются элементы i, ... ,n и каждый элемент i оказывается сепарабельным над полем, полученным присоеди нением предыдущих элементов 1, 2 ,…,i-1 то расширение
= (1, ... ,n)
сепарабельно над .
В частности, сумма, разность, произведение и частное сепарабедьных элементов сепарабельны.
Далее, если сепарабелен над , а поле сепарабельно над , то эле мент сепарабелен над . Это объясняется тем, что удовлетворяет некото рому уравнению с конечным числом коэффициентов 1, ... ,m из и, сле довательно, сепарабелен над (1, ... ,m). Тем самым сепарабельно и расширение
(1,..., m, ).
Наконец, имеет место следующее предложение: числа изоморфизмов конечного сепарабельного расширения над полем равно степени расширения ( : ).
4. Бесконечные расширения полей.
Каждое поле получается из своего простого подполя с помощью конечного или бесконечного расширения. В этой главе рассматри ваются бесконечные расширения полей, сначала алгебраические, а затем — трансцендентные.
4.1. Алгебраически замкнутые поля
Среди алгебраических расширений заданного поля важную роль играют, конечно, максимальные алгебраические расширения, т. е. такие, которые не допускают дальнейшего алгебраического расширения. Существование таких расширений будет доказано в настоящем параграфе.
Чтобы поле было максимальным алгебраическим расшире нием, необходимо следующее условие: каждый многочлен кольца [x] полностью разлагается на линейные множители. Это условие является и достаточным. Действительно, если каждый многочлен в [x] разлагается на линейные множи тели, то все простые многочлены в [x] линейны и каждый эле мент любого алгебраического расширения ' поля оказывается корнем некоторого линейного многочлена x — a в [x], т. е. совпадает с некоторым элементом a поля .
Поэтому дадим следующее определение:
Поле называется алгебраически замкнутым, если любой многочлен в [x] разлагается на линейные множители.
Равнозначное с этим определение таково: поле , алгебраически замкнуто, если каждый отличный от константы многочлен из [x] обладает в хоть одним корнем, т. е. хоть одним линейным множителем в [x].
Действительно, если такое условие выполнено и произвольно взятый многочлен f(x) разлагается на неразложимые множители, то все они должны быть линейными.
«Основная теорема алгебры» утверждает, что поле комплексных чисел алгебраически замкнуто. Следующим примером алгебраически замкнутого поля может служить поле всех комплексных алгебраических чисел, т. е. множе ство тех комплексных чисел, которые удовлетворяют какому-либо уравнению с рациональными коэффициентами. Комплексные корни уравнения с алгебраическими коэффициентами являются и в самом деле алгебраическими не только над полем алгебраических чисел, но и над полем рациональных чисел, т. е. сами являются алгебра ическими числами.
Здесь мы покажем, как построить алгебраически замкнутое расширение произвольно заданного поля P и притом чисто алгебраическим путем. Штейницу принадлежит следующая
Основная теорема. Для каждого поля P существует алгебраически замкнутое алгебраическое расширение . С точностью до эквивалентности это расширение определено однозначно: любые два алгебраически замкнутых алгебраических расширения , ' поля P эквивалентны.
Доказательству этой теоремы мы должны предпослать несколько лемм:
Лемма 1. Пусть , — алгебраическое расширение поля Р. Достаточным условием для того, чтобы было алгебраически замкнутым, является разложение на линейные множители любого многочлена из P[x] в кольце [x].
Доказательство. Пусть f(x) — произвольный многочлен из [x]. Если он не разлагается на линейные множители, то можно присоединить некоторый его корень и прийти к собст венному надполю '. Элемент является алгебраическим над , а является алгебраическим расширением поля P; следовательно, элемент алгебраичен и над Р. Поэтому он является корнем некоторого многочлена g(x) из P[x]. Этот многочлен разлагается в [x] на линейные множители. Следовательно, —корень неко торого линейного множителя в [x], т. е. принадлежит полю , что противоречит предположению.
Лемма 2. Если поле P вполне упорядочено, то кольцо много членов P[x] может быть вполне упорядочено и притом так, что в этом упорядочении поле P будет отрезком.
Доказательство. Определим отношение порядка между многочленами f(x) из P[x] следующим образом: пусть f(x)<g(x), когда выполнено одно из условий:
1) степень f(x) меньше степени g(x);
2) степень f(x) равна степени g(x) и равна n, т. е.
f(x) = а0хn + ...+ аn , g (x) = b0хn + ... + bn
и при некотором индексе k :
аi = bi для i
ak<bk, в смысле упорядочения поля Р.
При этом для многочлена 0 делается исключение: ему присваи вается степень 0. Очевидно, что таким способом получается неко торое упорядочение, в смысле которого P[x] вполне упорядочено. Показывается это так: в каждом непустом множестве многочле нов есть непустое подмножество многочленов наименьшей степени; пусть таковая равна п. В этом подмножестве есть непустое под множество многочленов, коэффициент а0 которых является первым в смысле имеющегося порядка среди свободных членов рассматривае мых многочленов; в указанном подмножестве есть в свою очередь подмножество многочленов с первым а1 и т. д. Подмножество с первым аn которое в конце концов получится, может состоять лишь из одного-единственного многочлена (так как а0, ..., аn определяются однозначно благодаря последовательно выполняе мому условию минимальности в выборе); этот многочлен является первым элементом в заданном множестве.
Лемма 3. Если поле P вполне упорядочено и заданы многочлен f(x) степени n и n символов 1 ..., n то поле P (1 ,..., n), в котором f(x) полностью разлагается на линейные множители
n
(x-i), строится единственным образом и является вполне
1
упорядоченным. Поле P в смысле этого порядка является отрезком.
Доказательство. Мы будем присоединять корни 1 ..., n последовательно, вследствие чего из P = Р0 последовательно будут возникать поля Р1, ..., Рn. Предположим, что Рi-1 = P(1 ..., i-1) — уже построенное поле и что P — отрезок в Рi-1; тогда Рi будет строиться так.
Прежде всего в силу леммы 2 кольцо многочленов Рi-1 [x] вполне упорядочивается. Многочлен f разлагается в этом кольце на неразложимые множители, среди которых на первом месте будут стоять x - 1,..., x - i-1; среди остальных множителей пусть fi(x) будет первым в смысле имеющегося порядка. Вместе с символом i обозначающим корень многочлена fi(x), мы опре деляем поле Рi = Pi-1 как совокупность всех сумм
h-1
ci
0
где h —степень многочлена fi(x). Если fi(x) линеен, то, конечно, мы полагаем Рi = Pi-1; символ i в этом случае не нужен. По строенное поле вполне упорядочивается с помощью следующего условия: каждому элементу поля
h-1
ci
0
сопоставим многочлен
h-1
cxi
0
и элементы поля упорядочим точно так же, как упорядочены соответствующие им многочлены.
Очевидно, тогда Рi-1 является отрезком в Рi, а потому и P — отрезок в Рi.
Тем самым поля Р1 ,..., Рn построены н вполне упорядочены. Поле Рn является искомым однозначно определенным полем P(1 ,..., n).
Лемма 4. Если в упорядоченном множестве полей каждое предшествующее поле является подполем последующего, то объеди нение этих полей является полем.
Доказательство. Для любых двух элементов , объединения существуют два поля , , которые содержат , и и из которых одно предшествует другому. В объемлющем поле опре делены элементы + и и именно так определяются эти элементы в каждом из полей, содержащих и , потому что из любых двух таких полей одно предшествует другому и явля ется его подполем. Например, чтобы доказать закон ассоциатив ности
• = • ,
найдем среди полей , , то, которое содержит два дру гих поля (наибольшее); в этом поле содержатся , и и в нем закон ассоциативности выполнен. Тем же способом проверяются все остальные правила вычислений с элементами объединения.
Доказательство основной теоремы распадается на две части: построение поля и доказательство единственности.
Построение поля .. Лемма 1 свидетельствует о том, что для построения алгебраически замкнутого расширения поля P достаточно построить такое алгебраическое расширение поля Р, чтобы каждый многочлен из Р[x] разлагался над этим расшире нием на линейные множители.
Будем считать, что поле Р, а потому и кольцо многочленов P[x], вполне упорядочены. Каждому многочлену f(x) сопоставим столько новых символов 1 ,..., n какова его степень.
Далее, каждому многочлену f(x) сопоставим два вполне упо рядоченных поля Рf, f, которые определяются следующим рекур рентным способом.
1. Поле Рf является объединением поля Р и всех полей g для g<f.
2. Поле Рf вполне упорядочивается так, чтобы Р и все поля Sg при g<f были отрезками в Рf
3. Поле Sf получается из Рf присоединением всех корней многочлена f с помощью символов 1 ,..., n в соответствии с лем мой 3.
Нужно доказать, что таким способом действительно одно значно определяются вполне упорядоченные поля Рf , Sf, если только уже определены все предыдущие Рg, Sg перечисленным выше требованиям.
Если выполнено требование 3, то прежде всего Рf— отрезок в Sf. Из этого и из требования 2 следует, что поле Р и каждое поле Sg (g<f) являются отрезками в Sf. Предположим, что рассматриваемые требования выполнены для всех предыдущих индексов f, так что
Р — отрезок в Sh при h<f,
Sg — отрезок в Sh при g<h<f.
Отсюда следует, что поле Р и поля Sh (h<f) составляют множество того типа, о котором говорит лемма 4. Следовательно, объединение этих полей снова является полем, которое в соот ветствии с требованием 1 мы должны обозначить через Рf. Струк тура вполне упорядоченного поля на Рf однозначно определяется требованием 2, потому что любые два элемента а, b из Рf, при надлежат одному из полей Р или Sg и поэтому связаны отноше нием a<b или а>b, которое должно сохраняться в Рf. Эго отношение порядка является одним и тем же во всех полях Р или Sg, которые содержат как а, так и b, потому что все эти поля являются отрезками друг друга. Итак, отношение порядка определено. То, что оно определяет вполне упорядоченное мно жество, очевидно, так как каждое непустое множество в Рf содержит по меньшей мере один элемент из Р или из некоторого поля Sg, а потому и первый элемент из Р или из Sg. Этот элемент одновременно является и первым элементом в .
Таким образом, поле Рf вполне упорядочивается с помощью требовании 1 и 2. Так как поле Sf, однозначно определяется требованием 3, поля Рf и Sf построены.
В силу условия 3 многочлен f(x) полностью разлагается на линейные множители в поле Sf. Далее, с помощью трансфинитной индукции показывается, что Sf является алгебраическим над Р. Действительно, предположим, что все поля Sg (g<f) уже алгебраические. Тогда и их объединение с полем Р, т.е. поле Рf, алгебраическое. Далее, поле Sf в силу условия 3 алгебраично над Рf, а потому алгебраично и над Р.
Составим теперь объединение всех полей Sf ; согласно лемме 4 оно является полем. Это поле алгебраично над Р и над ним раз лагаются все многочлены f (так как каждый многочлен f разла гается уже над Sf). Следовательно, поле алгебраически замкну то (лемма 1).
Единственность поля . Пусть и '— два поля, являющиеся алгебраическими и алгебраически замкнутыми рас ширениями поля Р. Докажем эквивалентность этих полей. Для этого будем считать, что оба поля вполне упорядочены. Построим для каждого отрезка из (само поле также считается од ним из таких отрезков) подмножество в ' и некоторый изо морфизм
P() Р().
Последний должен удовлетворять следующим рекуррентным соот ношениям.
1. Изоморфизм P() Р() должен оставлять каждый эле мент поля Р на месте.
2. Изоморфизм P() Р() при должен быть про должением изоморфизма Р() Р(').
3. Если обладает последним элементом a, так что = {a}, и если а — корень неразложимого в Р () многочлена f(x), то элемент а' должен быть первым корнем соответствующего в силу Р() Р('), многочлена f(x) во вполне упорядоченном поле '.
Нужно показать, что этими тремя требованиями действительно определяется изоморфизм P() Р(), если только он уже оп ределен для всех предыдущих отрезков . Здесь необходимо различать два случая.
Первый случай. Множество не имеет последнего элемента. Тогда каждый элемент а принадлежит некоторому предыдущему отрезку ; поэтому является объединением отрезков , а по тому Р() — объединением полей Р() для . Так как каж дый из изоморфизмов Р(Á) @Р(Á') является продолжением всех предыдущих, то каждому элементу при всех этих изоморфизмах сопоставляется лишь один элемент '. Поэтому существует одно и только одно отображение P(Â) → Р(¢), продолжающее все предыдущие изоморфизмы Р(Á)→ Р(Á'), а именно —отображение '. Очевидно, оно является изоморфизмом и удовлетворяет требованиям 1 и 2.
Второй случай. Множество имеет последний элемент а; сле довательно, ={а}. Вследствие требования 3 элемент а', со поставляемый элементу а, однозначно определен. Так как а' над полем Р(') (в смысле рассматриваемого изоморфизма) удовлетво ряет «тому же» неразложимому уравнению, что и а над Р(), то изоморфизм Р(Á)→Р(Á') (и в том случае, когда пусто, т. е. тождественный изоморфизм РР) продолжается до изоморфизма Р(Á, a) Р(Á', a), при котором а переходит в а'. Каждым из приведенных выше требований этот изоморфизм определен однозначно, потому что каждая рациональная функция (а) с коэффициентами из обязательно переходит в функцию '(а') с соответствующими коэффициентами из '. То, что так определенный изоморфизм P(Â) Р(¢) удовлетворяет требованиям 1 и 2, очевидно.
Тем самым построение изоморфизма P(Â)→Р(¢) завершено. Обозначим через " объединение всех полей Р(¢); тогда существует изоморфизм Р()" или ", оставляющий на месте каждый элемент поля Р. Так как поле алгебраически замкнуто, таким же должно быть и ", а потому " совпадает со всем полем . Отсюда следует эквивалентность полей и .
Значение алгебраически замкнутого расширения данного поля состоит в том, что с точностью до эквивалентности оно содержит все возможные алгебраические расширения этого поля. Точнее:
Если — алгебраически замкнутое алгебраическое расширение поля Р и — произвольное алгебраическое расширение поля Р, то внутри существует расширение 0, эквивалентное расширению .
Доказательство. Продолжим до некоторого алгебраи чески замкнутого алгебраического расширения '. Оно будет алгебраическим и над Р, а потому эквивалентным расширению . При каком-то изоморфизме, переводящем ' в и сохраняющем неподвижным каждый элемент из Р, поле переходит в некоторое эквивалентное ему подполе 0 в .
4.2. Простые трансцендентные расширения.
Каждое простое трансцендентное расширение поля , как мы знаем, эквивалентно полю частных (x) кольца многочленов [x]. Поэтому мы изучим это поле частных
= (x).
Элементами поля служат рациональные функции
= f(x)/g(x).
Это представление можно считать несократимым (f и g взаимно просты). Наибольшая из степеней многочленов f(x) и g(х) назы вается степенью функции .
Теорема. Каждый отличный от константы элемент сте пени п трансцендентен над и поле (x) — алгебраическое рас ширение поля () степени п.
Доказательство. Представление = f(х)/g(х) будем считать несократимым. Тогда элемент х удовлетворяет уравнению
g(x) - f(x)=0
с коэффициентами из (). Эти коэффициенты не могут быть все равны нулю. Действительно, если бы все они равнялись нулю и ak был бы при той же степени х любым ненулевым коэффициентом многочлена g(x), а bk — ненулевым коэффициентом многочлена f(x), то должно было бы иметь место равенство
ak - bk = 0
откуда = bk/ak = const, что противоречит предположению. Сле довательно, элемент х алгебраичен над ().
Если бы элемент был алгебраическим над , то и х был бы алгебраическим над , что, однако, не так. Следовательно, элемент трансцендентен над .
Элемент х является корнем многочлена степени n
g(z) - f(z)
в кольце ()(z). Этот многочлен неразложим в ()[z], потому что иначе он был бы разложим п в кольце [, z], и, так как он линеен по , один из множителей должен был бы зависеть не от , а лишь от z. Но такого множителя не может быть, потому что g(z) и f(z) взаимно просты.
Следовательно, элемент х является алгебраическим степени п над полем (). Отсюда следует утверждение о том, что ((x) : ()) = n
Для дальнейшего отметим, что многочлен
g(z) - f(z)
не имеет множителей, зависящих только от z (т. е. лежащих в [z]). Это утверждение остается верным, когда заменяется своим значением f(х)/g(х) и умножается на знаменатель g(х) тем самым многочлен
g(z)f(x) - f(z)g(x)
кольца [x, z] не имеет множителей, зависящих только от z.
Из доказанной теоремы вытекают три следствия.
1. Степень функции — f(х)/g(х) зависит лишь от полей () и (x), а не от того или иного выбора порождающего элемента х.
2. Равенство Д () = (х) имеет место тогда и только тогда, когда имеет степень 1, т. е. является дробно-линейной функ цией. Это означает: порождающим элементом поля, кроме эле мента х, может служить любая дробно-линейная функция от x и только такая функция.
3. Любой автоморфизм поля (х), оставляющий на месте каждый элемент поля , должен переводить элемент x в какой-либо порождающий элемент поля. Обратно, если х переводится в какой-либо порождающий элемент х = (ax+b)/(cx+d) и каждая функция (х) — в функцию (х), то получается автоморфизм, при котором все элементы из остаются на месте. Следовательно,
Все автоморфизмы поля (x) над полем являются дробно-линейными подстановками
x = (ax+b)/(cx+d), ad – bc 0.
Важной для некоторых геометрических исследований является
Теорема Люрота. Каждое промежуточное поле , для которого (x), является простым трансцендентным расширением: = ().
Доказательство. Элемент х должен быть алгебраическим над , потому что если — любой элемент из не принадлежащий полю , то, как было показано, элемент х является алгебраическим над () и тем более алгебраическим над . Пусть неразложимый в кольце многочленов [z] многочлен со старшим коэффициентом 1 и корнем x имеет вид
f0(z) = zn+a1zn-1+…+an. (1)
Выясним строение этого многочлена.
Элементы ai являются рациональными функциями от x. С помощью умножения на общий знаменатель их можно сделать целыми рациональными функциями и, кроме того, получить многочлен относительно x с содержанием 1:
f( x, z) =b0(x)zn+b1 (x)zn-1+…+bn(x).
Степень этого многочлена по х обозначим через т, а по z — через п.
Коэффициенты ai = bi / b0 из (1) не могут все быть независимыми от х, так как иначе х оказался бы алгебраическим элементом над ; поэтому один из них, скажем,
= ai = bi(x)/ b0(x),
должен фактически зависеть от х; запишем его в несократимом виде:
= g(x)/h(x)
Степени многочленов g(х) и h(х) не превосходят т. Многочлен
g(z) - h(z) = g(z) – (g(x)/h(x))h(z)
(не являющийся тождественным нулем) имеет корень z = x, а потому он делится на f 0(z) в кольце [z]. Если перейти от этих рациональных по х многочленов к целым по х многочленам с содержанием 1, то отношение делимости сохра нится, и мы получим
h(x)g(z)-g(x)h(z) = q(x, z)f(x, z).
Левая часть в этом равенстве имеет степень по х, не превосхо дящую т. Но справа уже многочлен f имеет степень т; следо вательно, степень левой части в точности равна т и q(х, z) не зависит от х. Однако зависящий лишь от z множитель не может делить левую часть (см. выше); поэтому q(х, z) является кон стантой:
h(x)g(z)-g(x)h(z) = qf(x, z).
Так как присутствие константы q роли не играет, строение мно гочлена f(х, z) описано полностью. Степень многочлена f(х, z) по х равна т следовательно (по соображениям симметрии), и степень по z равна т, так что m = п. По меньшей мере одна из степеней многочленов g(x) и h(х) должна фактически достигать значения m, следовательно, и функция должна иметь степень т по х.
Тем самым, так как с одной стороны установлено равенство
((х):()) = т,
а с другой — равенство
((x):) = m;
то, поскольку содержит (),
(: ()) =1,
= ().
Заключение.
В данной курсовой работе рассмотрены основные алгебраические расширения полей, во-первых, ввиду той фундаментальной роли, которую поля играют в современной математике, во-вторых, ввиду относительной простоты этого понятия.
В курсовой работе были рассмотрены следующие виды расширений числового поля P:
Простое алгебраическое расширение поля.
Составное алгебраическое расширение поля.
Сепарабельные и несепарабельные расширения.
Бесконечные расширения полей.
Анализируя работу можно сделать некоторые выводы.
Из рассмотренных в первых двух частях расширений, таких как:
простые алгебраические расширения;
конечные расширения;
составные алгебраические расширения.
Следует, что все эти виды расширений совпадают и, в частности, исчерпываются простыми алгебраическими расширениями поля P.
Литература
1. Л.Я. Куликов. Алгебра и теория чисел.— М.: Высш. Школа,1979.—528-538с.
2. Б.Л. Ван-дер-Варден. Алгебра.— М.,1976 — 138-151с.,158-167с.,244-253с.
3. Э.Ф. Шмигирев, С.В. Игнатович. Теория многочленов.— Мозырь 2002.
2

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ