Лабораторная работа

Решение нелинейных уравнений

Задание

N =07

М=2

Дано уравнение: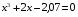

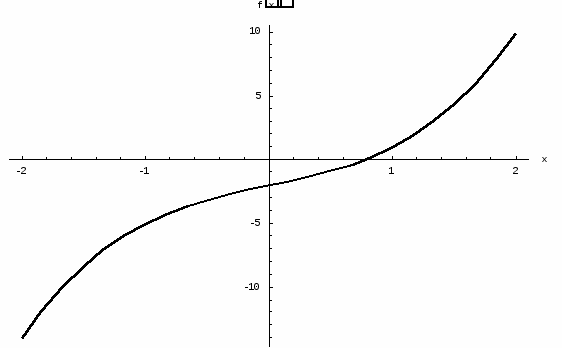
1. Найти все решения уравнения графически.

1. Уточнить значение одного из действительных решений уравнения с точностью до

 = 0,001:

1. *методом половинного деления;

1. *методом Ньютона - Рафсона;

1. методом секущих;

1. конечно-разностным методом Ньютона;

1. *методом простой итерации;

1. *методом хорд и касательных

1. комбинированным методом Ньютона.

3. Результаты расчетов оформить таблично с кратким описанием каждого использованного метода: расчетные формулы, выбор начального приближения, критерий остановки и пр.

3. Из методов пункта 2 задание на лабораторную работу предусматривает обязательное использование 4-х методов, отмеченных звездочками, и одного из остальных методов по усмотрению студента.

нелинейный уравнение графический ньютон итерация

1. Решение уравнения графически:

2. Метод половинного деления

Расчетная формула: следующее значение x получается делением отрезка пополам.

Начальное приближение: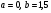

Критерий остановки: 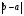<2; .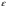

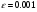Таблица результатов

Метод половинного деления

k

a_k

b_k

x_k

f(a_k)

f(b_k)

f(x_k)

|b_k-a_k|

f(x_k)*f(a_k)

f(x_k)*f(b_k)

|b_k-a_k|<2ε

0

0

1,5

0,75

-2,070

4,305

-0,148

1,5

0,306360

-1,000000

-

1

0,75

1,5

1,125

-0,148

4,305

1,604

0,75

-0,237392

6,905220

-

2

0,75

1,125

0,938

-0,148

1,604

0,631

0,375

-0,093388

1,012120

-

3

0,75

0,938

0,844

-0,148

0,631

0,219

0,188

-0,032412

0,138190

-

4

0,75

0,844

0,797

-0,148

0,219

0,03

0,094

-0,004440

0,006570

-

5

0,75

0,797

0,774

-0,148

0,03

-0,058

0,047

0,008584

-0,001740

-

6

0,774

0,797

0,786

-0,058

0,03

-0,012

0,023

0,000696

-0,000360

-

7

0,786

0,797

0,792

-0,012

0,03

0,011

0,011

-0,000132

0,000330

-

8

0,786

0,792

0,789

-0,012

0,011

-0,001

0,006

0,000012

-0,000010

-

9

0,789

0,792

0,791

-0,001

0,011

0,007

0,003

-0,000007

0,000080

-

10

0,789

0,791

0,790

-0,001

0,007

0,003

0,002

-0,000003

0,000020

-

11

0,789

0,790

0,790

-0,001

0,003

0,003

0,001

+

3. Метод Ньютона – Рафсона

Расчетная формула: 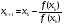, где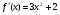

Начальное приближение:.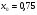

Критерий остановки: |f(x_k+1)-f(x_k)|<ε; .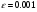

Таблица результатов:

Метод Ньютона – Рафсона

k

x_k

f(x_k)

f'(x_k)

|f(x_k+1)-f(x_k)|<ε

0

0,75

-0,1481

3,688

-

1

0,79

0,003

3,872

-

2

0,789

-0,0008

3,868

+

4. Метод Ньютона – Рассела

Расчетная формула: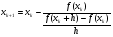

Начальное приближение: : x = 0,75

Критерий остановки: |f(x_k+1)-f(x_k)|<ε, .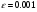

Таблица результатов:

Метод Ньютона – Рассела

k

x_k

h

x_k+h

f(x_k)

f(x_k+h)

|f(x_k+1)-f(x_k)|<ε

0

0,75

1

1,75

-0,1481

6,789

-

1

0,771

1

1,771

-0,0697

7,027

-

2

0,781

1

1,781

-0,0316

7,141

-

3

0,785

1

1,785

-0,0163

7,187

-

4

0,787

1

1,787

-0,0086

7,211

-

5

0,788

1

1,788

-0,0047

7,222

-

6

0,789

1

1,789

-0,0008

7,234

-

7

0,789

1

1,789

-0,0008

7,234

+

5. Метод простой итерации

Расчетная формула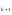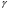:. x=(x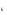), где 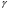(x)=x - k f(x), k=0.11

Начальное приближение: x = 0,75

Критерий остановки: |x_k+1-x_k|≤ε; .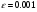

Таблица результатов

Метод простой итерации

k

x_k

φ(x_k)

|x_k+1-x_k|≤ε

0

0,5

0,604

-

1

0,604

0,675

-

2

0,675

0,720

-

3

0,720

0,748

-

4

0,748

0,765

-

5

0,765

0,775

-

6

0,775

0,781

-

7

0,781

0,784

-

8

0,784

0,786

-

9

0,786

0,787

-

10

0,787

0,788

-

11

0,788

0,789

-

12

0,789

0,789

+

6. Метод хорд и касательных

Расчетная формула: ,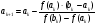

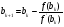,где .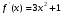

Начальное приближение: ,

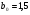
Критерий остановки: ; .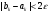

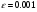Таблица результатов:

Метод хорд и касательных

k

a_k

b_k

f(a_k)

f(b_k)

f'(a_k)

f'(b_k)

f''(a_k)

f''(b_k)

f(a_k) *f''(a_k)

f(b_k) *f''(b_k)

|b_k-a_k|<2ε

0

0

1,5

-2,070

4,305

2

8,75

0

9

0

38,745

-

1

0,487

1,022

-0,980

1,041

2,712

5,133

2,922

6,132

-2,86

6,383

-

2

0,746

0,852

-0,163

0,252

3,67

4,178

4,476

5,112

-0,73

1,288

-

3

0,788

0,803

-0,005

0,054

3,863

3,934

4,728

4,818

-0,02

0,26

-

4

0,789

0,792

-0,001

0,011

3,868

3,882

4,734

4,752

-0,01

0,052

-

5

0,789

0,79

-0,001

0,003

3,868

3,872

4,734

4,74

-0,01

0,014

+

Вывод

Название метода

Вычислительная сложность

Сложность

реализации

Глобальная

сходимость

Скорость

сходимости

h

Произв.

Метод Ньютона-Рафсона

-

+

+++

-

квадратичная

Метод половинного деления

-

-

+

+

линейная

Метод простой итерации

-

-

+

-

линейная

Конечно-разностный метод

+

-

++

-

сверхлинейная (при хорошем выборе h)

Метод секущих

-

+

++

-

сверхлинейная

Метод хорд и касательных

-

+

+++

квадратичная

Метод хорд

-

+

+++

-

Сначала лин., потом сверхлин.