ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

КАМСКАЯ ГОСУДАРСТВЕННАЯ ИНЖЕНЕРНО-ЭКОНОМИЧЕСКАЯ АКАДЕМИЯ

КАФЕДРА «Прикладной информатики и управления»

Контрольная работа

По дисциплине: «Вычислительная математика»

По теме: «Решение систем нелинейных уравнений методом Ньютона».

Выполнил: студент (ЦДО)

Шевченко С.Н.

№спец. 230102 (АСОИУ)

Проверил: Обухова Л.Г.

г. Набережные Челны – 2010 г.

СОДЕРЖАНИЕ

Введение

3

1. ОСНОВНЫЕ ЭТАПЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

4

2. МЕТОД НЬЮТОНА (МЕТОД КАСАТЕЛЬНЫХ)

7

Заключение

11

Список использованной литературы

12

ВВЕДЕНИЕ

В данной работе необходимо рассмотреть решение систем нелинейных уравнений методом Ньютона.

Данный метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов», адресованной в 1669 году английскому математику Исааку Барроу, и в работе «Метод флюксий и бесконечные ряды» или «Аналитическая геометрия». В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения 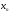, а последовательность полиномов и в результате получал приближённое решение .

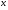1 ОСНОВНЫЕ ЭТАПЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.

Нелинейным уравнением называется уравнение вида

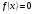, (1.1)

где 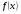- нелинейная функция вида:

- нелинейная алгебраическая функция (полином или многочлен);

- тригонометрическая, логарифмическая, показательная функция;

- комбинирование этих функций, например .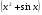

Решением нелинейного уравнения (1.1) называется такое значение 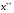, которое при подстановке в уравнение (1.1) обращает его в тождество.

На практике не всегда удается найти точное решение. В этом случае решения уравнения (1.1) находят с применением приближенных (численных) методов.

Приближенным решением нелинейного уравнения (1.1) называется такое значение 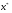, при подстановке которого в уравнение (1.1) последнее будет выполняться с определенной степенью точности.

Нахождение приближенных решений составляет основу численных методов и вычислительной математики. Решение нелинейных уравнений и их систем распадается на два этапа: отделение корней уравнений и уточнение корней нелинейных уравнений.

На первом этапе необходимо исследовать уравнение и выяснить, имеются корни или нет. Если корни имеются, то необходимо определить их количество и затем найти интервалы, в каждом из которых находится только один корень, т.е. отделить корни.

Первый способ отделения корней – графический. Данный метод позволяет определить количество корней на отрезке, но не единственность корня. Если 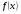имеет простой аналитический вид, то, исходя из уравнения (1.1), можно построить график функции 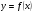. Тогда точки пересечения графика функции с осью абсцисс будут являться приближенными значениями корней исходного нелинейного уравнения. Если 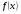имеет сложный аналитический вид, то можно представить её в виде разности двух более простых функций 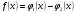. Так как 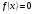, то выполняется равенство 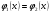. После построения графиков и 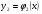задача решения нелинейного уравнения сводится к поиску абсцисс точек пересечения двух графиков, которые и будут являться приближенными значениями корней уравнения (1.1).

Второй способ отделения корней – аналитический. Процесс отделения корней здесь основывается на следующих теоремах:

1) если функция 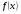непрерывна на отрезке 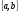и на концах отрезка принимает значения разных знаков (т.е. 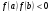), то на 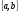содержится хотя бы один корень.

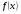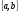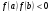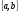2) если функция непрерывна на отрезке , выполняется условие вида и производная сохраняет знак на , то на отрезке имеется единственный корень.

3) если функция 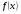является многочленом n-й степени и на концах отрезка 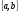принимает значения разных знаков, то на 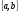имеется нечетное количество корней. Если на концах отрезка 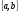функция меняет знак, то уравнение (1.1) либо не имеет корней на 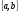, либо имеет четное количество корней.

При аналитическом методе исследований необходимо выявить интервалы монотонности функции 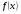. Для этого необходимо найти критические точки 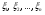, т.е. точки, в которых первая производная равна нулю или не существует. Тогда вся числовая ось разбивается на интервалы монотонности 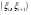, на каждом из которых определяется знак производной 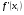, где . Затем выделяются те интервалы монотонности 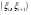, на которых функция 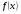меняет знак, то есть выполняется неравенство 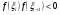. На каждом из этих интервалов для поиска корня используются методы уточнения корней.

Одним из наиболее распространенных методов уточнения корня на отрезке является метод Ньютона (метод касательных).

2 МЕТОД НЬЮТОНА (МЕТОД КАСАТЕЛЬНЫХ).

Пусть известно, что нелинейное уравнение 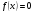имеет на отрезке 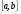единственный вещественный корень 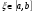. Причем, производные 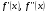- непрерывны и сохраняют определенный знаки на отрезке 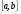. Требуется найти этот корень с заданной точностью 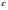. Найдем какое-либо 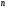-е приближенное значение корня 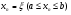и уточним его методом Ньютона следующим образом.

Пусть

. (2.1)

По формуле Тейлора получим

.

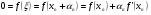Следовательно, .

Внося эту правку в формулу (2.1), получим рабочую формулу метода Ньютона вида:

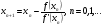(2.2)

Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой 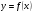касательной, проведенной в некоторой точке 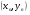этой кривой.

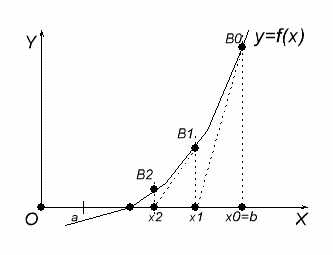
Для определенности положим 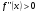и 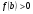. Выберем начальное приближение 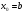, для которого 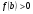. Проведем касательную к кривой 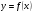в точке 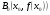. За первое приближение 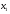берем точку пересечения касательной с осью 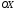. На кривой определим точку 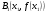и проведем касательную к кривой 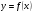в этой точке. Найдем следующее приближение 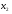и так далее (рис. 2.1).

Рис. 2.1.

Составим уравнение касательной в точке :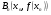

.

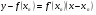Полагая , из уравнения касательной получим итерационную формулу метода Ньютона:

.

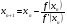Если в качестве начального приближения взять другой конец отрезка 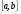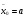, то следующее приближение .

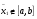Рассмотрим метод определения необходимого конца отрезка, выбираемого в качестве начального приближения .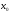

Теорема. Если 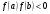и производные 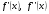не равны нулю и сохраняют определенные знаки на отрезке 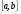, то исходя из начального приближения 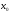, удовлетворяющего неравенству 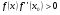, по методу Ньютона, заданному формулой (2.2), можно вычислить единственный корень 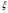уравнения с любой степенью точности.

Доказательство.

Пусть для определенност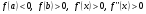и при 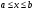(остальные случаи рассматриваются аналогично).

Из неравенства 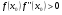следует, что 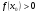, т.е. .

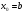Докажем, что все приближения 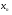расположены правее 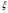, т.е. 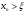, а значит .

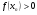Доказательство проведем методом индукции:

а) ;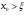

б) предположим, что ;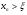

в) докажем, что .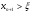

Точное решение уравнения (1.1) можно представить в виде

.

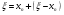Применяя формулу Тейлора, получим:

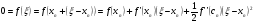(2.3)

где .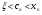

Так как по условию теоремы 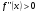, то последнее слагаемое в соотношении (2.3) положительное, следовательно,

.

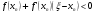Отсюда, в силу того, что 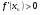, получим:

.

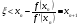Таким образом доказали, что все последовательные приближения 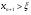, т.е. находятся правее 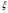, и, следовательно .

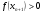Из соотношения (2.2), учитывая знак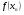и и 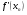, следует, что 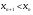, т.е. последовательные приближения 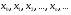образуют ограниченную монотонную убывающую последовательность, т.е. эта последовательность имеет конечный предел, который обозначим 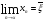. Перейдем к пределу при 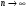в левой и правой частях соотношения (2.2), получим:

,

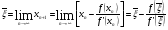т.е. 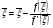. Отсюда следует, что 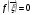, т.е. 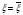. А это означает, что последовательные приближения 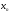сходятся к корню уравнения (1.1), что и требовалось доказать.

Вывод: в методе Ньютона в качестве начального приближения 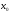выбирается тот конец отрезка 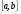, которому отвечает ордината того же знака, что и 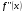, т.е. выполняется достаточное условие сходимости

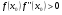. (2.4)

Следует заметить, что чем больше числовое значение 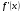в окрестности корня 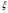, тем меньше правка 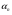. Поэтому методом Ньютона удобно пользоваться, когда в окрестности искомого корня 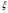график функции 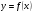имеет большую крутизну (т.е. 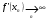, тогда 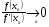). Если кривая 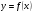вблизи точки пересечения с осью 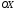почти горизонтальна (т.е. 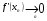, тогда 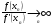), то применять метод Ньютона для решения уравнения (1.1) не рекомендуется.

Метод Ньютона можно рассматривать как частный случай метода простых итераций, если считать 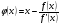. Тогда достаточное условие сходимости метода простых итераций примет вид:

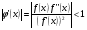для всех 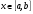. (2.5)

Если выполнено условие (2.5), то итерационный процесс, заданный формулой (2.2), будет сходиться при произвольном выборе начального приближения .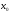

ЗАКЛЮЧЕНИЕ

В данной работе было рассмотрено решение систем нелинейных уравнений методом Ньютона.

Достоинства метода Ньютона:

1) обладает достаточно большой скоростью сходимости, близкой к квадратичной;

2) достаточно простое получение итерационной формулы.

Недостатки метода Ньютона:

1) сходится не при любом выборе начального приближения;

2) применим только в тех случаях, когда производная функции на всей области определения не равна нулю.

В некоторых случаях для решения систем нелинейных уравнений целесообразно применять модифицированный метод Ньютона.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Гутер Р.С., Овчинский Б.В. «Элементы численного анализа и математической обработки результата опыта» М., Наука 1970., 432 с.

2. Красильников В.В. Математичемкие методы в экономике. Набережные Челны, 1999, 475 с.

3. Горбунов Д.А., Комиссарова Е.М. Вычислительная математика: Учебное пособие. Казань: Изд-во Казан. гос. техн. ун-та, 2008. 148 с.