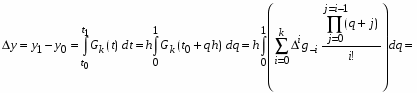Міністерство освіти і науки України

Національний технічний університет

“ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ"

Кафедра “Обчислювальної техніки та програмування"

Реферат з курсу “Численные методы"

Тема: “Решение уравнений в конечных разностях”

Виконав:

студент групи

Перевірив:

Харків

Содержание

1. Разностная аппроксимация дифференциальных уравнений

Используя описанные выше соотношения между операторами дифференцирования и операторами конечных разностей несложно в заданном интервале изменения независимой переменной получить конечно-разностную аппроксимации дифференциальных уравнений системой алгебраических рекуррентных формул или уравнений. Основная идея аппроксимации схематически представляется так: В заданном в общем виде дифференциальном уравнении или системе

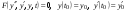
производится замена независимой переменной t ее представлением в заданном интервале путем преобразования 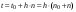, а искомая функция и ее производные выражаются посредством конечно-разностных соотношений через некоторое число равномерно расположенных с шагом 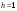ординат 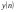, начиная с : , , ,..., : .

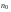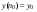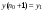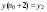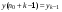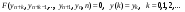Разрешив неявную форму разностного выражения относительно старшей ординаты 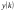, получим рекуррентную формулу, из которой по известным k начальным ординатам можно последовательно найти ординаты всего искомого процесса. Вопрос лишь в том, где взять нужное количество начальных ординат. Благополучно разрешима задача лишь в случае, когда производная аппроксимируется разностью первого порядка:

.

После приведения исходной системы к системе уравнений первого порядка каждая искомая переменная получает значение при , равное своему начальному условию. В результате рекуррентный вычислительный процесс оказывается определенным и позволяет вычислить на очередном шаге значения всех переменных:

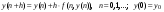
или

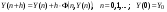
где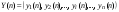 - вектор переменных,

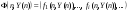- вектор производных.

Такой вычислительный процесс в литературе получил название численного интегрирования систем дифференциальных уравнений по явному методу Эйлера. Основная трудность здесь заключается в выборе шага интегрирования для нецелочисленной независимой переменной t.

2. Решение линейных разностных уравнений

Система линейных разностных уравнений может быть в ряде случаев решена и аналитически. Решение представляется в виде алгебраического выражения от целочисленной переменной. Методика решения аналогична той, что применяется и при решении линейных дифференциальных уравнений.

Используется тот факт, что общее решение неоднородного линейного уравнения представляется взвешенной суммой системы фундаментальных решений однородного уравнения и одного частного решения уравнения неоднородного. Воздействие неоднородности на характер общего решения не связано с конкретными значениями начальных условий. Именно это позволяет находить лишь одно частное решение уравнения с правой частью. Число фундаментальных решений однородного уравнения определяется порядком последнего.

В качестве частных решений для линейных уравнений обычно используют функции, инвариантные по отношению к операции сдвига, т.е. функции, не изменяющие своей структуры при переносе начала координат. В конечно-разностных уравнениях это показательные функции:

Где p - некоторый параметр-константа. Количество частных решений определится числом параметров 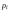, для которых 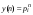будет обращать разностное уравнение в тождество. Общее решение составляется в виде суммы частных решений, умноженных на коэффициенты, определяемые конкретными начальными условиями. Рассмотрим пример решения линейного неоднородного уравнения третьего порядка.

Пусть требуется заменить рекуррентный вычислительный процесс с псевдокодом следующего вида:

на формульное выражение для 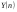, как функции от n, позволяющее выборочно вычислять значение любого члена последовательности. Для этого в рекуррентном операторе цикла заменим оператор ': =' на символ равенства '=' и запишем полученное уравнение в форме неоднородного разностного уравнения относительно :

.

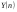В качестве фундаментальной системы функций возьмем 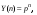тогда характеристическое уравнение примет следующий вид:

.

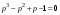Решив уравнение, найдем корни: , следовательно, частными решениями однородного уравнения будут:

Частное решение неоднородного уравнения (с правой частью) попробуем найти в виде функции, которая будет пропорциональна квадратуре от правой части с неизвестными коэффициентами:

Для нахождения коэффициентов a и b подставим в уравнение 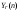и приравняем коэффициенты при одинаковых степенях n в левой и правой частях полученного равенства. Последовательно выполняя сказанное, имеем:

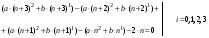
Раскрыв скобки и сгруппировав слагаемые при различных степенях n, получим

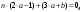
откуда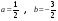 и частное решение примет вид

.

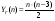Общее решение для конкретных начальных условий ищем в виде суммы частных решений:

.

Константы 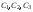находим из уравнений, получаемых после подстановки в общее решение значений для 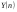при :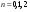

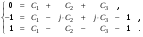
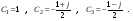
В результате, общее решение неоднородного уравнения будет:

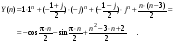
Для примера выпишем несколько первых членов ряда, полученных вычислением этого выражения: [0, - 1, 1, 2, 2, 5, 11, 16, 20, 27, 37, 46, 54, 65, 79, 92, 104, 119, 137, 154, 170,...]

3. Рекуррентные формулы для решения разностных уравнений

Интегрирование системы нелинейных разностных уравнений первого порядка по Эйлеру аналитически выполнить, как правило, не удается. Поэтому решение задачи получают в численном виде путем вычисления очередных значений процессов по рекуррентным формулам, начиная с известных начальных условий:

,

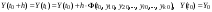Где 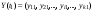- очередное значение вектора решений,

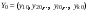- вектор начальных значений.

Основной проблемой процесса численного интегрирования является выбор величины шага h. Формула Эйлера вносит в процесс численного решения погрешность, пропорциональную h. Это несложно увидеть, если сравнить вычисляемое при интегрировании уравнения выражение с первыми слагаемыми ряда Тейлора для точки :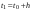

.

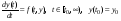По Эйлеру

,

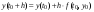или иначе:

,

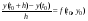а по Тейлору:

,

или иначе:

.

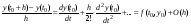Отбрасываемые члены разложения 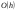характеризуют погрешность формулы Эйлера, в которую входят слагаемые с h в первой степени и выше.

Результат интегрирования можно улучшить, если по найденному значению , 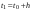вычислить значение производной, т.е. 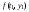, и в формулу Эйлера ввести среднее арифметическое двух производных: для начала и для конца интервала . Модифицированная формула примет следующий вид:

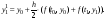
Такого рода уточнения (итерации) можно повторять, пока в выражении

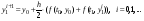модуль разности станет .

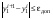Погрешность модифицированной формулы будет пропорциональна . Это показывается аналогично предыдущему сопоставлению.

Продифференцируем исходное уравнение

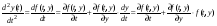
и подставим выражение производной в ряд Тейлора. В результате получим:

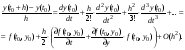
Аналогичное выражение для первых двух слагаемых и остаточного ряда второй степени от h получается и для модифицированной формулы Эйлера, если в последней осуществить разложение 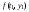в ряд Тейлора по степеням h:

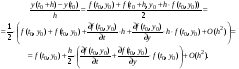
Усреднение производных с итерационным уточнением их для нескольких точек интервала особенно наглядно представлено в формулах Рунге-Кутта четвертого порядка :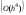

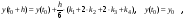
где

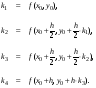
Здесь производная вычисляется в трех точках интервала h (на концевых точках и дважды в средней точке интервала для итерационного уточнения), после чего окончательное приращение находится как взвешенное среднее.

4. Интерполяционные рекуррентные формулы

Достоинством методов Эйлера и Рунге-Кутта является их самоначинаемость независимо от порядка формулы, а основной недостаток в том, что число вычислений правой части неоднородной системы дифференциальных уравнений равно порядку формулы.

В этом плане выгодно отличаются формулы интегрирования, построенные на основе интерполяционных многочленов, опорными точками которого являются предыдущие, уже вычисленные значения переходного процесса. Широко используемым методом интегрирования с таким подходом могут служить формулы интегрирования Адамса.

4.1 Интерполяция конечными разностями “назад”

Возьмем в качестве примера интерполяционный многочлен Ньютона для интерполирования функции “назад”, т.е. в сторону меньших значений независимой переменной по отношению к текущему ее значению:

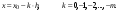
Построение такого интерполяционного многочлена удобно осуществлять с применением повторных конечных разностей “назад”:

.

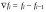Взаимосвязь оператора 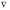и рассмотренных выше операторов 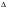и характеризуется следующими соотношениями:

Выразим ординату функции, отстоящую от текущей на k шагов назад, через ординату функции 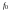в текущей точке и выполним ряд эквивалентных преобразований с названными линейными операторами:

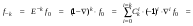
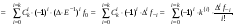
Если положить

, то

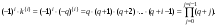
Таким образом, интерполяционный многочлен Ньютона для интерполирования “назад” принимает вид:

,

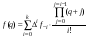где принимает целые значения для ,

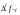- i-тая повторная конечная разность “вперед", вычисляемая по значениям функции в соответствии с таблицей:

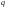
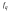
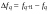
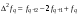
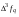
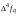
-4

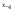
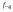
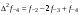
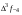
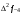
-3

-

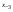
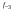
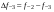
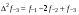
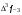
-2

-

-

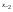
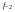
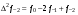
-1

-

-

-

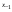
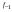
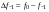
0

-

-

-

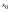
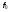
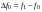
1

-

-

-

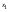
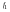
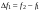
В таблице жирным шрифтом выделены конечные разности от нулевого порядка и выше, которые входят в интерполяционную формулу Ньютона.

4.2 Рекуррентные формулы Адамса

Пусть теперь требуется найти решение уравнения

.

для которого уже каким-либо способом найдены k+1 значений решения 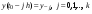, что, естественно, определяет и соответству-ющие значения 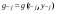. На основе построим интерполя-ционный многочлен k-той степени:

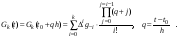
Приращение решения на внешнем интервале 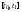можно получить, проинтегрировав интерполяционный многочлен в интервале 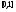по переменной q, предварительно сделав замену переменных:

.

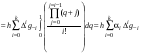Интегралы в каждом слагаемом зависят только от i и определяют коэффициенты, с которыми повторные разности входят в выражение для приращения. Таким образом, экстраполяционная формула Адамса имеет вид:

,

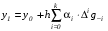где первые пять коэффициентов приведены в таблице

i

0

1

2

3

4

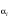
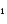
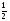
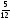
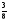
Появление нового значения 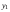требует для очередного шага вычислить новые значения повторных разностей. Для этого в таблице разностей заполняется по одной дополнительной клеточки в каждом столбце после одного-единственного вычисления правой части. В этом и состоит основное достоинство экстраполяционных формул.

В формулу Адамса вместо повторных разностей можно подставить их выражения через ординаты 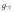. Например, ограничившись 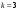, получим

Модификаций у формул Адамса много. Можно менять не только интерполяционные многочлены, но и вычислять приращения в пределах нескольких шагов. Наиболее простой получается формула для k=4, в которой приращение вычисляется на интервале в два шага :

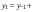
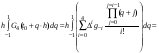
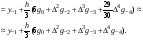
Если построить интерполяционный многочлен Ньютона не от точки , а от точки 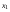и опять вычислить для k=4 приращение в интервале 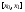, то последнее может служить контролем за точностью вычислений:

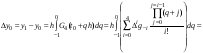
Литература

1.Беллман Р., Кук К. Дифференциально-разностные уравнения. М.: Мир, 1967. - 548с.

2.Волков Е.А. Численные методы. СПб.: Лань, 2004. - 248с.

3.Гельфонд А.О. Исчисление конечных разностей. М.: Наука, 1967. - 375с.

4.Калашников В.И. Аналоговые и гибридные вычислительные устройства: Учеб. пособие. - Харьков: НТУ “ХПИ", 2002. - 196с.

5.Коддингтон Э.А., Левинсон Н. Теория обыкновенных дифференциальных уравнений. Новосибирск: Изд-во иностр. лит., 1958. - 474с.

6.Скалкина М.А., “О колебаниях решений уравнений в конечных разностях", Изв. вузов. Матем., 1959, № 6, 138-144