Решение задач по высшей математике

Размещено на http://www.

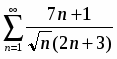
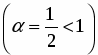
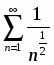
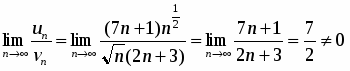
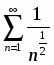
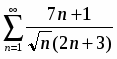
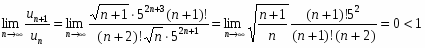
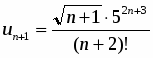
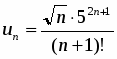
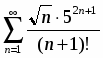
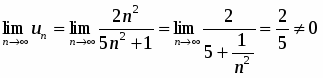
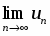
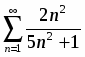
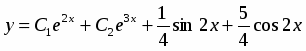
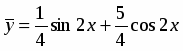
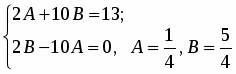
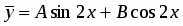
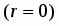
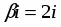
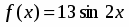
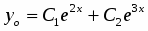
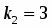
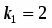
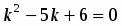
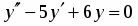
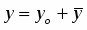
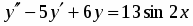
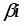
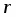
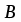
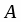
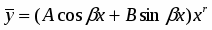
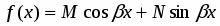
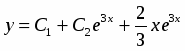
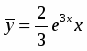
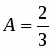
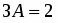
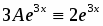
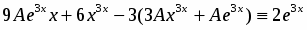
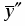
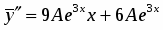
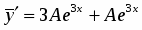
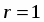
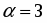
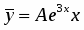
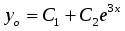
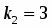
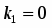
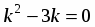
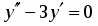
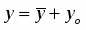
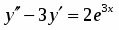
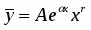
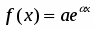
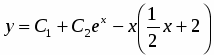
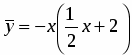
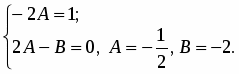
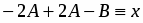
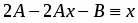
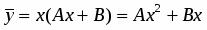
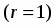
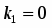
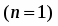
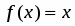
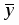
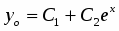
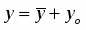
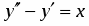
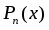
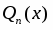
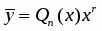
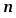
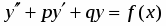
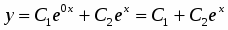
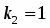
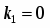
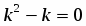
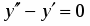
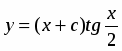
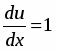
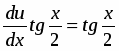
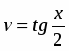
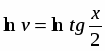
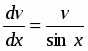
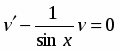
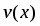
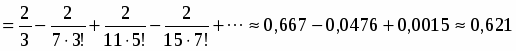
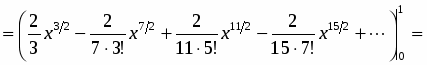
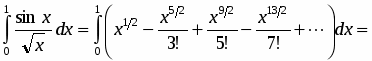
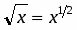
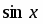
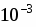
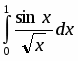
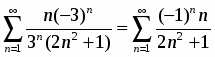
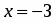
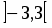
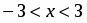
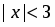
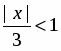
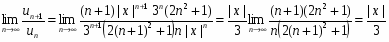
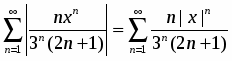
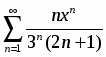
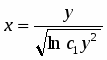
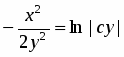
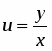
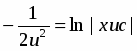
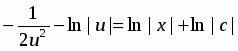
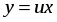
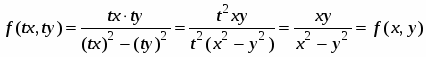
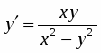
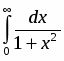
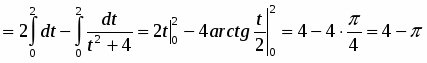
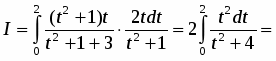
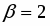
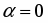
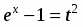
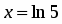
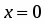
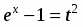
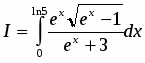
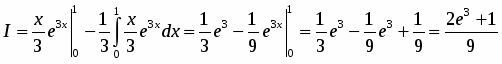
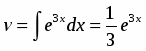
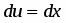
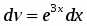
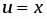
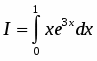
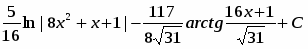
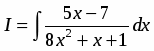
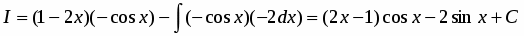
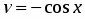
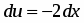
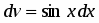
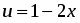
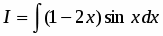
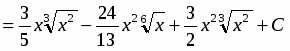
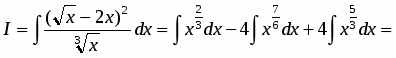
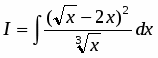
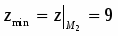
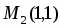
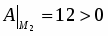
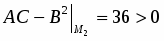
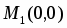
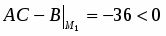
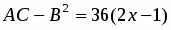
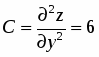
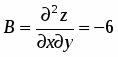
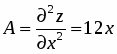
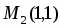
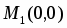
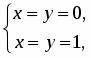
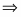
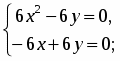
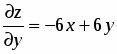
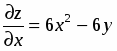
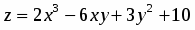
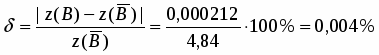
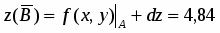
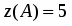
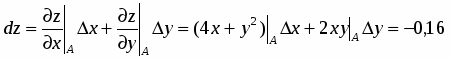
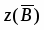
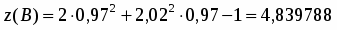
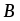
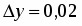
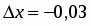
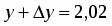
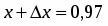
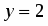
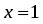
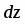
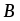
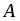
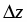
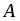
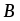
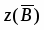
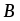
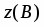
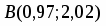
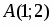
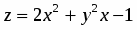
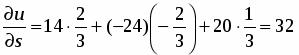
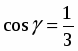
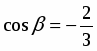
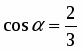
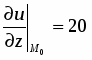
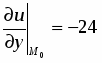
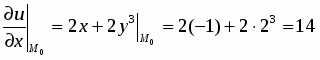
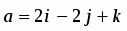
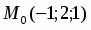
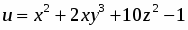
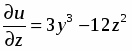
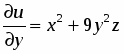
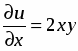
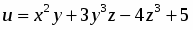
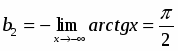
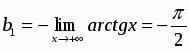
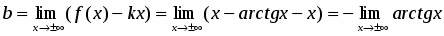
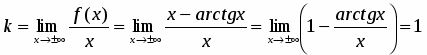
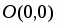
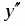
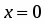
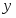
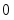
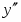
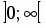
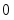
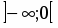
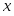
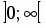
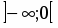
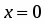
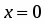
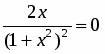
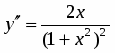
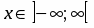
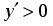
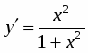
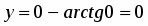
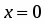
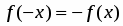
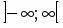
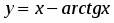
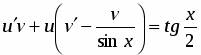
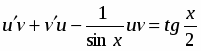
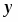
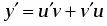
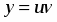
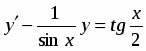
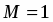
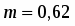
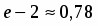
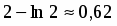
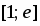
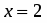
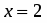
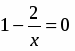
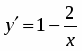
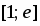
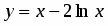
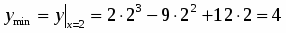
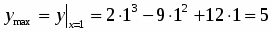
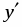
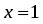
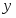
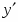
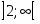
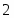
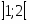
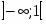
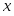
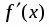
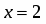
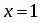
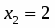
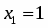
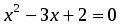
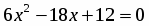
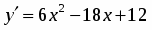
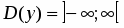
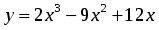
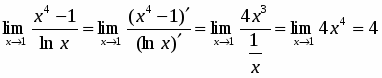
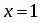
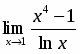
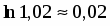
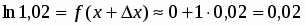
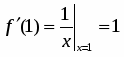
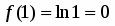
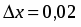
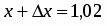
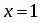
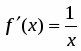
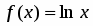
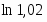
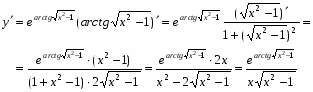
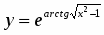
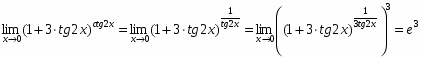
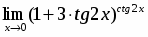
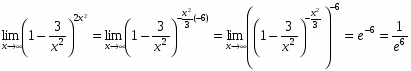
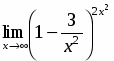
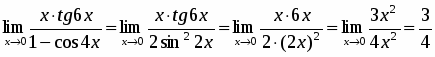
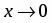
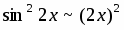
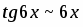
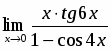
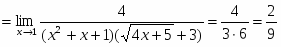
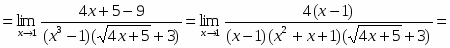
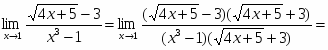
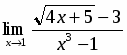
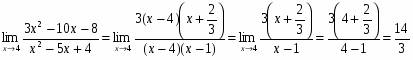
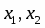
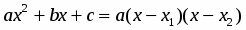
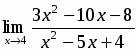
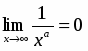
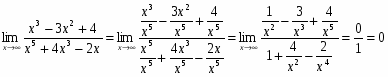
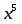
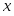
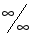
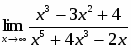
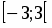
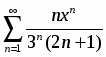
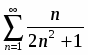
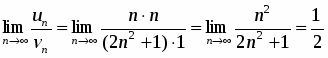
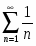
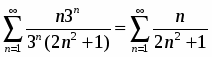
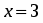
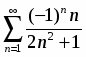
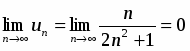
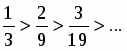
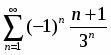
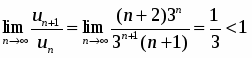
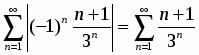
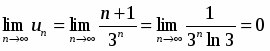
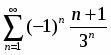
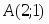
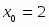
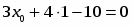
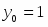
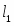
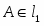
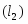
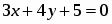
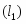
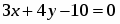
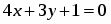
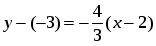
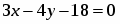
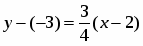
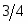
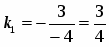
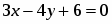
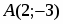
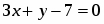
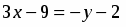
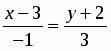
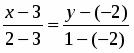
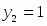
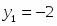
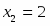
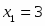
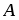
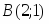
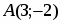
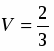
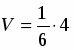
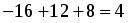
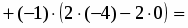
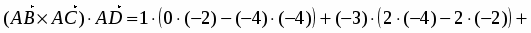
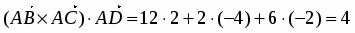
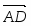
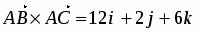
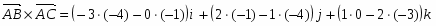
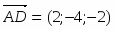
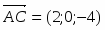
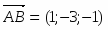
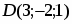
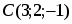
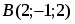
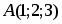
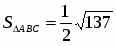
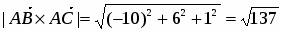
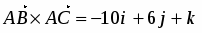
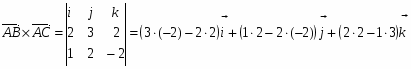
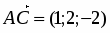
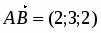
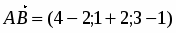
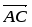
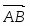
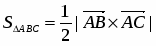
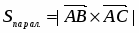
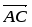
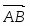
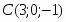
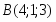
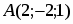
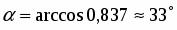
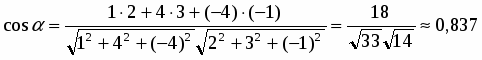
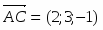
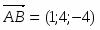
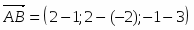
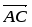
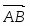
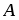
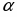
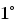
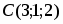
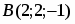
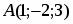
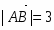
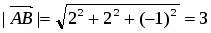
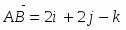
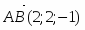
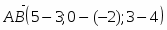
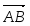
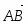
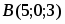
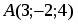
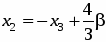
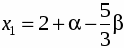
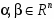
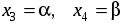
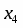
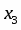
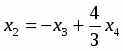
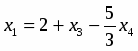
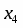
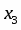
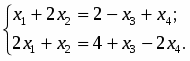
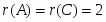
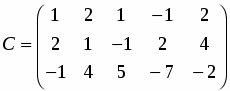
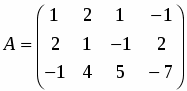
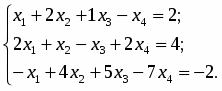
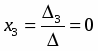
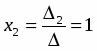
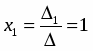
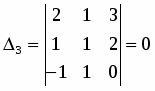
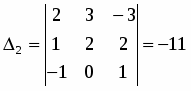
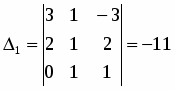
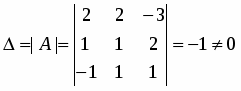
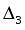
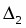
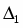
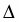
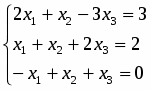
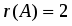
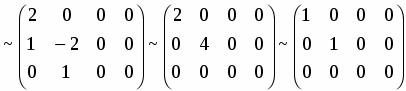
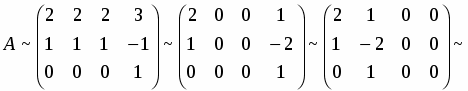
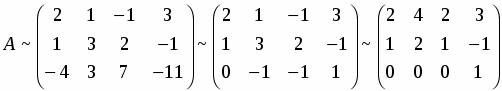
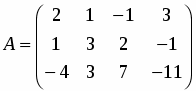
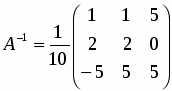
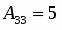
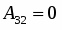
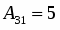
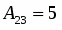
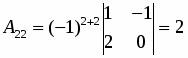
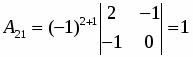
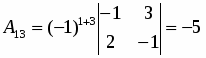
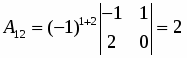
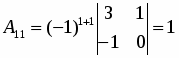
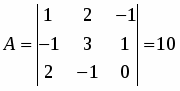
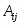
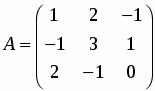
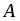
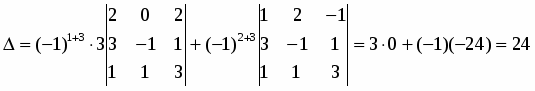
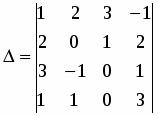
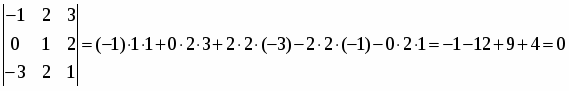
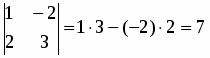
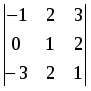
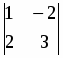
КОНТРОЛЬНАЯ РАБОТА

Решение задач по высшей математике

Задача 1

Вычислить определители:

;

Решение

Задача 2

Вычислить определитель:

Решение

Используя теорему Лапласа, разложим определитель по элементам третьего столбца

Задача 3

Найти матрицу, обратную к матрице .

Решение

Находим определитель матрицы и все алгебраические дополнения :

;

Ответ: Обратная матрица имеет вид:

Задача 4

С помощью элементарных преобразований вычислить ранг матрицы

Решение

Прибавляя к последней строке учетверенную вторую строку и сокращая затем последнюю строку на , а после этого складывая последний столбец со вторым и третьим последовательно, получим

Знак ~ обозначает, что матрицы получены одна из другой с помощью элементарных преобразований и их ранги равны. Сокращая второй столбец на два и вычитая первый столбец со всех остальных столбцов, а затем вычитая последнюю строку из первой и меняя местами столбцы, получаем

Ответ: Ранг матрицы равен двум.

Задача 5

Решить следующую систему линейных алгебраических уравнений по правилу Крамера:

;

Решение

Вычислим главный определитель системы и вспомогательные определители , ,.

;

По формуле Крамера, получим

;

; .

Задача 6

Исследовать на совместность систему линейных алгебраических уравнений и, в случае положительного ответа, найти её решение.

Решение

Матрица и имеют вид

Их ранги равны . Система совместна. Выделим следующую подсистему

Считая и известными, решение подсистемы находим по формулам Крамера . Оно имеет вид

; ,

где , - могут принимать произвольные значения. Пусть , где Тогда ответом будет служить множество

Задача 7

Даны начало и конец вектора . Найти вектор и его длину.

Решение

Имеем , откуда или .

Далее , т.е. .

Задача 8

Даны вершины треугольника , и . Найти с точность до угол при вершине .

Решение

Задача сводится к нахождению угла между векторами и :

, ; . Тогда , .

Задача 9

Даны вершины треугольника , и . Вычислить площадь этого треугольника.

Решение

Так как площадь треугольника равна половине площади параллелограмма, построенного на векторах и как на сторонах, т.е. , то . Найдем векторы и :

Вычислим их векторное произведение:

Откуда

. Следовательно, (кв. ед.).

Задача 10

Даны вершины треугольной пирамиды , , и . Найти ее объем.

Решение

Имеем , и . Найдем векторное произведение

Этот вектор скалярно умножим на вектор :

Это смешанное произведение можно найти непосредственно по приведенной формуле:

Следовательно, объем:

, (куб. ед.).

Задача 11

Составить уравнение прямой, проходящей через точки и .

Решение

За первую вершину примем (на результат это не влияет); следовательно,

Имеем

, , ,

Ответ: - общее уравнение искомой прямой.

Задача 12

Составить уравнение прямой, проходящей через точку , параллельно и перпендикулярно прямой .

Решение

Найдем угловой коэффициент данной прямой: . Согласно условиям параллельности и перпендикулярности двух прямых, угловой коэффициент параллельной прямой будет равен , а перпендикулярной прямой будет равен –4 /3. Составляем уравнения искомых прямых:

1) параллельной: , - общее уравнение прямой, параллельной данной;

2) перпендикулярной: , - общее уравнение прямой, перпендикулярной к данной.

Задача 13

Найти расстояние между двумя параллельными прямыми и .

Решение

Выберем на одной из данных прямых точку . Пусть . Для определения координат точки на прямой одну координату выберем произвольно, а вторую определим из уравнения. Возьмём ; тогда , и . По формуле расстояния от точки до прямой находим:

; .

Задача 14

Исследовать на абсолютную и условную сходимость

Решение

Проверим выполнение условий теоремы Лейбница

а)

б)

(при вычислении предела применялось правило Лопиталя). Условия выполняются, следовательно, ряд сходится. Исследуем ряд на абсолютную сходимость.

Имеем:

Тогда по признаку Даламбера:

, и ряд, составленный из абсолютных величин элементов исходного ряда, будет сходится. Следовательно, ряд сходится абсолютно.

а)

б) ,

следовательно ряд - сходится.

2) Пусть . Тогда . Применим признак сравнения, сравнивая его с расходящимся гармоническим рядом . Имеем

Таким образом, ряд - расходится.

Ответ

Область сходимости ряда есть интервал .

Задача 15

Вычислить предел .

Решение

Для вычисления этого предела непосредственно применить указанные теоремы нельзя, так как пределы функций, находящихся в числителе и знаменателе, не существуют. Здесь имеется неопределенность вида , для раскрытия которой в данном случае следует числитель и знаменатель дроби разделить на наибольшую степень переменной , т.е. на :

так как при .

Задача 16

Вычислить придел

Решение

Так как предел знаменателя равен нулю, то теорема 3 неприменима. Здесь имеется неопределенность вида . Для раскрытия этой неопределенности в числителе и знаменателе следует выделить бесконечно малый множитель, на который затем сократить дробь. Для этого воспользуемся формулой разложения квадратного трехчлена на множители

, где - его корни.

Тогда

Задача 17

Вычислить предел .

Решение

Умножив числитель и знаменатель на выражение, сопряженное к числителю, получим:

Задача 18

Вычислить предел .

Решение

Легко убедиться, что и при .

Поэтому

Задача 19

Вычислить предел

Решение

Для того, чтобы воспользоваться вторым замечательным пределом, в показателе степени выделим величину, обратную второму слагаемому основания и получим

Задача 20

Найти предел .

Решение

Задача 21

Продифференцировать функцию .

Решение

Задача 22

Вычислить при помощи дифференциала .

Решение

Пусть . Тогда . Обозначим: ; . Отсюда . Находим и .

Итак, .

Задача 23

Найти .

Решение

Подстановка в заданную функцию значения приводит к неопределенности вида . Применив правило Лопиталя, получим:

Задача 24

Исследовать на экстремум функцию

Решение

1. Находим область определения функции:.

2. Находим производную функции: .

3. Находим критические точки, решая уравнение или . Критические точки , .

4. Область определения функции разбиваем критическими точками и на интервалы, в каждом из которых определяем знак , делаем вывод о характере монотонности функции на каждом из интервалов и отмечаем наличие экстремумов.

—

Возрастает

Max

убывает

Min

Возрастает

При переходе через критическую точку производная меняет знак с “+” на “-”. Значит, в этой точке функция имеет максимум:

Аналогично устанавливаем, что

Задача 25

Найти наибольшее и наименьшее значения функции

на отрезке .

Решение

1. Находим критические точки заданной функции:

2. Убеждаемся в том, что точка принадлежит отрезку.

3. Вычисляем: ;.

4. Сравниваем числа ;и находим:

; .

Задача 26

Найти общее решение уравнения

Решение

Это неоднородное линейное дифференциальное уравнение первого порядка. Его решение ищем в виде , тогда . Подставляя и в исходное уравнение, получим

или . (1)

Задача 27

Исследовать функцию .

Решение

1. Функция определена и непрерывна на интервале . Поэтому точек разрыва и вертикальных асимптот у графика функции нет.

2. Функция нечетная, поскольку . Это значит, что график функции симметричен относительно начало координат.

3. Положив , получим , т.е. кривая проходит через начало координат.

4. Функция не периодична.

5. Находим первую производную . Производная для всех . Это значит, что функция возрастает на всей числовой оси. Поэтому экстремумов она не имеет.

6. Находим вторую производную и приравниваем её к нулю: . Точка будет критической точкой. Точкой разбиваем область определения функции на интервалы и , являющиеся интервалами знакопостоянства второй производной.

—

выпуклая

вогнутая

Поскольку при переходе через точку производная меняет знак, то точка будет точкой перегиба искомой кривой.

7. Выясним наличие наклонных асимптот:

;

; .

Следовательно, наклонными асимптотами будут прямые:

и .

Задача 28

Найти частные производные функции

Решение

Задача 29

Найти производную функции в точке в направлении вектора .

Решение

Задача 30

Даны функция и точки и . Вычислить:

точное значение функции в точке ;
приближенное значение функции в точке, исходя из её значения в точке , заменив приращение при переходе от точки к точке дифференциалом ;
относительную погрешность, возникающую при замене на .

Решение

По условию , , , . Поэтому , . Находим точное значение функции в точке :

Находим приближенное значение :

;

; .

Вычисляем относительную погрешность:

Задача 31

Найти экстремумы функции

Решение

Находим критические точки:

;

откуда и - точки, где частные производные равны нулю. Исследуем эти точки с помощью достаточных условий

;

. Поэтому экстремума в точке функция не имеет.

, . Поэтому функция в точке имеет минимум: .

Задача 32

Вычислить неопределенный интеграл

Решение

Возводим в квадрат числитель и почленно делим на знаменатель. Затем, применяя свойства, получаем первый интеграл таблицы:

Задача 33

Вычислить неопределенный интеграл

Решение

Принимая в подынтегральном выражении , , получим , . Поэтому

Проверка. .

Задача 34

Вычислить неопределенный интеграл

Решение

Сделав замену переменной

Получим

Задача 35

Вычислить .

Решение

Полагаем , ; тогда , .

Интегрируя по частям, находим

Задача 36

Вычислить

Решение

Положим . Подстановка значений и в уравнение дает и . Таким образом,

Задача 37

Найти .

Решение

По определению

Задача 40

Найти общее решение уравнения .

Решение

Так как

то данное уравнение есть однородное дифференциальное уравнение. Заменив в исходном уравнении , получим уравнение или .

Это уравнение с разделяющимися переменными. Разделив их, получим

Проинтегрировав последнее уравнение, найдем

или .

Подставив , общее решение исходного уравнения запишем в виде , а после преобразования .

Задача 38

Найти область сходимости степенного ряда

Решение

Составим ряд из абсолютных величин

По признаку Даламбера имеем:

следовательно , , , и на интервале ряд сходится.

Проверим его сходимость на концах интервала:

1) Пусть . Тогда - знакочередующийся ряд. Для его анализа применим теорему Лейбница:

Задача 14

Вычислить с точностью до .

Решение

Разложив в ряд и поделив почленно на , получим:

Выбираем функцию такой, чтобы .

Тогда .

Интегрируем и находим или .

Подставив найденную функцию в (1), получим ещё одно уравнение

, , ; .

Следовательно, - общее решение заданного уравнения.

Задача 42

Найти общее решение дифференциального уравнения:

Решение

Составим характеристическое уравнение

. Так как и , то общим решением будет

Частное решение неоднородного уравнения подбирается в зависимости от вида функции .

Пусть , , представляет собой многочлен степени с действительными коэффициентами. Тогда частное решение следует искать в виде:

где - многочлен той же степени, что и многочлен , но с неизвестными коэффициентами, а - число корней характеристического уравнения, равных нулю.

Задача 43

Найти общее решение уравнения .

Решение

Ищем общее решение в виде , где - общее решение соответствующего однородного уравнения, - частное решение неоднородного уравнения. Так как - многочлен первой степени и один корень характеристического уравнения , то частное решение надо искать в виде

Подберем коэффициенты и так, чтобы решение удовлетворяло данному уравнению

Приравняв коэффициенты при одинаковых степенях левой и правой частей тождества, получим

Следовательно, , а - искомое общее решение.

Пусть . Тогда частное решение неоднородного уравнения , где - число корней характеристического уравнения, равных .

Задача 44

Найти общее решение уравнения .

Решение

Ищем решение в виде . Решим однородное уравнение . Корни характеристического уравнения равны и . Следовательно, . Частное решение ищем в виде (так как , ). Найдем , а . Подставляя , и в исходное уравнение, получим

, , .

Значит, - частное решение, а - общее решение.