Решетки субнормальных и f-субнормальных подгрупп
Курсовая работа
"Решетки субнормальных и  -субнормальных подгрупп"
-субнормальных подгрупп"
Введение
В теории конечных групп одним из центральных понятий является понятие  -субнормальной подгруппы. Изучению свойств субнормальных подгрупп конечных групп положило начало в 1939 г. известная работа Виландта [10], оказавшая огромное влияние на развитие всей теории конечных групп в последующие годы.
-субнормальной подгруппы. Изучению свойств субнормальных подгрупп конечных групп положило начало в 1939 г. известная работа Виландта [10], оказавшая огромное влияние на развитие всей теории конечных групп в последующие годы.
В первом разделе курсовой работы изучаются основные положения теории субнормальных подгрупп. Важнейшим достижением данной теории является результат Виландта о том, что множество всех субнормальных подгрупп любой конечной группы образует решетку.
Формации, т.е. классы групп, замкнутые относительно фактор-групп и подпрямых произведений, всегда находились в поле деятельности исследователей по теории конечных групп. Однако вплоть до 1963 г. формационное развитие теории конечных групп шло лишь по пути накопления фактов, относящихся к различным конкретным формациям, из которых наиболее популярными были формация разрешимых групп и ее подформации, составленные из абелевых, нильпотентных и сверхразрешимых групп. Хотя теория конечных групп никогда не испытывала недостатка в общих методах, идеях и нерешенных проблемах, все же обилие полученных результатов с неизбежностью привело к необходимости разработки новых общих методов и систематизирующих точек зрения. Толчок, произведенный работой Гашюца [8], вызвал целую лавину исследований и привел к возникновению нового направления – теории формаций.
В теории формаций одним из важнейших понятий является понятие  -субнормальных подгрупп, которое является естественным расширением субнормальных подгрупп. Поэтому, конечно, возникает задача о построении теории
-субнормальных подгрупп, которое является естественным расширением субнормальных подгрупп. Поэтому, конечно, возникает задача о построении теории  -субнормальных подгрупп, аналогичной теории субнормальных подгрупп Виландта.
-субнормальных подгрупп, аналогичной теории субнормальных подгрупп Виландта.
Во втором разделе курсовой работы рассматриваются минимальные не  -группы.
-группы.
В третьем разделе приводится описание локальных наследственных формаций, обладающих решеточным свойством для  -субнормальных подгрупп.
-субнормальных подгрупп.
1. Субнормальные подгпруппы и их свойства
Определение. Пусть  – подгруппа группы
– подгруппа группы  . Цепь подгрупп
. Цепь подгрупп
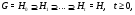
в которой 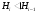 для любого
для любого 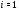 ,
, 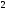 ,…,
,…,  , называется субнормальной
, называется субнормальной 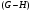 -цепью, а число
-цепью, а число  – длиной этой цепи. Наименьшее
– длиной этой цепи. Наименьшее  , при котором существует хотя бы одна субнормальная
, при котором существует хотя бы одна субнормальная 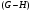 -цепь длины
-цепь длины  , называется дефектом подгруппы
, называется дефектом подгруппы  в
в  и обозначается через
и обозначается через 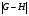 .
.
Определение. Пусть  – подгруппа группы
– подгруппа группы  . Если существует хотя бы одна субнормальная
. Если существует хотя бы одна субнормальная 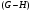 -цепь, то подгруппа называется субнормальной, обозначается
-цепь, то подгруппа называется субнормальной, обозначается 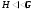 .
.
Лемма. Если  субнормальна в
субнормальна в  , и
, и  субнормальна в
субнормальна в  , то
, то  субнормальна в
субнормальна в  .
.
 субнормальна в
субнормальна в  , следовательно, по определению субнормальной подгруппы существует субнормальная
, следовательно, по определению субнормальной подгруппы существует субнормальная 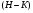 -цепь
-цепь
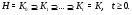
 субнормальна в
субнормальна в  , следовательно, существует субнормальная
, следовательно, существует субнормальная 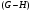 -цепь
-цепь

Таким образом, мы получили субнормальную 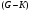 -цепь
-цепь
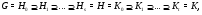
то есть  субнормальна в
субнормальна в  по определению. Лемма доказана.
по определению. Лемма доказана.
Теорема. Если подгруппа  субнормальна, но не нормальна в
субнормальна, но не нормальна в  , то существует такой элемент
, то существует такой элемент 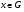 , что
, что
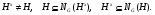
Доказательство. Пусть 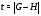 – дефект подгруппы
– дефект подгруппы  в группе
в группе  . Рассмотрим субнормальную
. Рассмотрим субнормальную 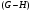 -цепь длины
-цепь длины  :
:
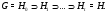
Из того, что  не нормальна в
не нормальна в  , следует, что
, следует, что 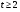 .
.  не нормальна и в
не нормальна и в 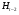 , иначе мы получаем противоречие с тем, что
, иначе мы получаем противоречие с тем, что  – дефект подгруппы
– дефект подгруппы  в группе
в группе  , так как в этом случае подгруппу
, так как в этом случае подгруппу 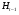 в цепи можно было опустить. Поэтому существует элемент
в цепи можно было опустить. Поэтому существует элемент 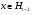 такой, что
такой, что 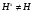 . Теперь имеем
. Теперь имеем
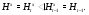
Так как 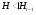 , то
, то 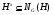 . С другой стороны,
. С другой стороны, 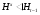 и
и 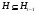 , откуда получаем
, откуда получаем  . Теорема доказана.
. Теорема доказана.
Определение. Пусть  – субнормальная подгруппа дефекта
– субнормальная подгруппа дефекта  в
в  . Субнормальная
. Субнормальная 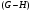 -цепь
-цепь
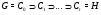
называется канонической, если для любой субнормальной 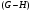 -цепи
-цепи
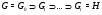
имеет место 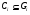 ,
, 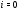 ,
,  ,…,
,…,  .
.
Другими словами, каноническая субнормальная цепь входит почленно в любую другую субнормальную цепь той же длины.
Теорема. Если  субнормальна в
субнормальна в  , то существует единственная каноническая субнормальная
, то существует единственная каноническая субнормальная 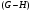 -цепь.
-цепь.
Доказательство. Пусть  – дефект подгруппы
– дефект подгруппы  в группе
в группе  . Будем рассматривать все возможные субнормальные
. Будем рассматривать все возможные субнормальные 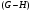 -цепи длины
-цепи длины  .
.
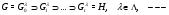
все субнормальные 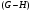 -цепи длины
-цепи длины  (
(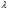 – второй индекс). Положим
– второй индекс). Положим  . Так как
. Так как  , то для любого
, то для любого 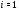 ,
, 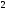 ,…,
,…,  мы имеем
мы имеем
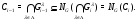
Таким образом, цепь
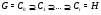
является субнормальной 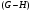 -цепью длины
-цепью длины  и, следовательно, не имеет повторений. Так как
и, следовательно, не имеет повторений. Так как 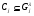 при любых
при любых 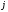 и
и 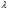 , то теорема доказана.
, то теорема доказана.
Теорема. Если  субнормальна в
субнормальна в  и
и  – подгруппа
– подгруппа  , то пересечение
, то пересечение 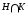 есть субнормальная подгруппа
есть субнормальная подгруппа  .
.
Доказательство. Рассмотрим субнормальную 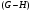 -цепь минимальной длины
-цепь минимальной длины  :
:
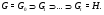
Положим  . Получаем цепь
. Получаем цепь
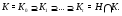
Ясно, что она будет субнормальной, так как 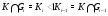 . Действительно, пусть
. Действительно, пусть 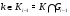 , значит,
, значит, 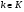 и
и 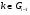 . Тогда для любого
. Тогда для любого  , так как
, так как 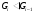 и
и 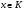 .
.
Мы получили субнормальную 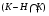 -цепь. Теорема доказана.
-цепь. Теорема доказана.
Следствие. Пусть  и
и  – подгруппы группы
– подгруппы группы  . Если
. Если  субнормальна в
субнормальна в  и
и  – подгруппа
– подгруппа  , то
, то  субнормальна в
субнормальна в  .
.
Доказательство. Пусть 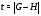 и цепь
и цепь
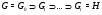
является субнормальной 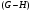 -цепью.
-цепью.
Положив 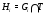 , получим субнормальную
, получим субнормальную 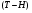 -цепь
-цепь
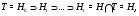
что и требовалось.
Теорема. Пусть  субнормальна в
субнормальна в  и
и  субнормальна в
субнормальна в  . Тогда пересечение
. Тогда пересечение 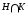 есть субнормальная подгруппа в
есть субнормальная подгруппа в .
.
Доказательство. Пусть  – наибольший из дефектов подгрупп
– наибольший из дефектов подгрупп  и
и  в группе
в группе  . Очевидно, существует (возможно, с повторениями) цепи
. Очевидно, существует (возможно, с повторениями) цепи

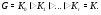
Положим 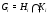 ,
, 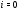 ,
,  ,…,
,…,  . Из
. Из  ,
,  следует, что
следует, что  нормальна в
нормальна в 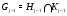 . Следовательно, цепь
. Следовательно, цепь
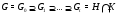
является субнормальной 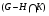 -цепью, что и доказывает теорему.
-цепью, что и доказывает теорему.
Лемма. Если  субнормальна в
субнормальна в  , а
, а 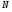 – нормальная подгруппа группы
– нормальная подгруппа группы  , то произведение есть субнормальная подгруппа группы
, то произведение есть субнормальная подгруппа группы  .
.
Доказательство.  субнормальна в
субнормальна в  , следовательно, существует субнормальная
, следовательно, существует субнормальная 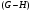 -цепь
-цепь
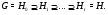
Следовательно, цепь

будет субнормальной.
Действительно, так как 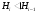 и
и 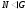 , то
, то 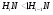 . Лемма доказана.
. Лемма доказана.
Лемма. Если подгруппы  и
и  субнормальны в
субнормальны в  и
и 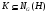 , топроизведение
, топроизведение 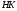 есть субнормальная подгруппа группы
есть субнормальная подгруппа группы  .
.
Доказательство. Если  нормальна в
нормальна в  , то результат следует по лемме 1.9.
, то результат следует по лемме 1.9.
Предположим, что  не нормальна в
не нормальна в  , то есть
, то есть 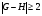 . Будем считать, что теорема верна для субнормальных подгрупп с дефектом меньшим
. Будем считать, что теорема верна для субнормальных подгрупп с дефектом меньшим  . Таким образом, если
. Таким образом, если 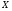 и
и 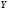 субнормальны в
субнормальны в  причем
причем 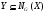 и
и  , то по индуктивному предположению
, то по индуктивному предположению 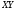 субнормальна в
субнормальна в  .
.
Пусть 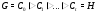 – каноническая субнормальная
– каноническая субнормальная 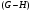 -цепь. Так как
-цепь. Так как  нормализует подгруппу
нормализует подгруппу  , то для любого
, то для любого 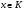 цепь
цепь
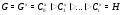
будет субнормальной 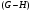 -цепью. По свойству канонической субнормальной
-цепью. По свойству канонической субнормальной 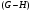 -цепи
-цепи  , а значит,
, а значит, 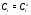 для любого
для любого 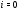 ,
,  ,…,
,…,  (по определеделению).
(по определеделению).
Следовательно,  содержится в
содержится в 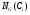 для любого
для любого 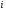 . Так как
. Так как 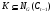 и
и  , то по индукции
, то по индукции 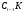 субнормальна в
субнормальна в  . По следствию 1.7.1
. По следствию 1.7.1  субнормальна в
субнормальна в 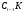 . Так как
. Так как 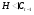 и
и 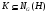 , то
, то 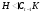 . Таким образом,
. Таким образом, 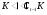 ,
, 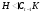 , а значит, по лемме 1.9 подгруппа
, а значит, по лемме 1.9 подгруппа 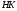 субнормальна в
субнормальна в 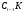 . К тому же
. К тому же 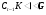 , то мы получаем
, то мы получаем 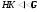 . Лемма доказана.
. Лемма доказана.
Теорема. Если  и
и  – субнормальный подгруппы группы
– субнормальный подгруппы группы  , то
, то 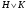 есть также субнормальная подгруппа
есть также субнормальная подгруппа  .
.
Доказательство. Положим 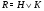 . Среди субнормальных подгрупп группы
. Среди субнормальных подгрупп группы  , содержащихся в
, содержащихся в 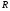 , выберем подгруппу
, выберем подгруппу  , имеющю наибольший порядок. По следствию 1.7.1
, имеющю наибольший порядок. По следствию 1.7.1  субнормальна в
субнормальна в 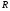 . Докажем, что
. Докажем, что  нормальна в
нормальна в 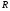 . Предположим противное, то есть что
. Предположим противное, то есть что  не нормальна в
не нормальна в 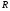 . Тогда по теореме 1.4 найдется такой элемент
. Тогда по теореме 1.4 найдется такой элемент  , что
, что 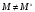 ,
, 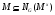 и
и 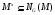 . Так как
. Так как  субнормальна в
субнормальна в 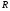 и
и  , то
, то 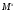 субнормальна в
субнормальна в 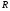 . Получается следующая ситуация:
. Получается следующая ситуация:  и
и 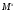 субнормальны в
субнормальны в  ,
, 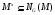 . По лемме 1.10
. По лемме 1.10 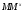 субнормальна в
субнормальна в  . Ввиду выбора
. Ввиду выбора  отсюда следует
отсюда следует 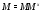 , что противоречит
, что противоречит 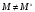 .
.
Итак,  нормальна в
нормальна в 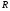 , а значит,
, а значит,  и
и  нормализуют подгруппу
нормализуют подгруппу  . По лемме 1.10
. По лемме 1.10  и
и  субнормальны в
субнормальны в  . Так как
. Так как 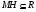 и
и 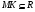 , то ввиду выбора
, то ввиду выбора  получаем
получаем  . Следовательно,
. Следовательно,  , откуда вытекает, что
, откуда вытекает, что 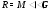 . Теорема доказана.
. Теорема доказана.
Объединим теоремы 1.8 и 1.11 в один результат.
Теорема (Виландт). Множество всех субнормальных подгрупп группы  образует подрешетку решетки
образует подрешетку решетки  .
.
Отметим одно часто используемое приложение теорем 1.4 и 1.12.
Теорема. Пусть 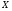 – некоторое непустое множество субнормальных подгрупп группы
– некоторое непустое множество субнормальных подгрупп группы  , удовлетворяющее следующим условиям:
, удовлетворяющее следующим условиям:
1) если  и
и 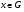 , то
, то  ;
;
2) если  ,
, 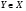 ,
, 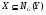 ,
, 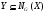 , то
, то 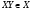 .
.
Тогда 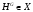 для любой подгруппы
для любой подгруппы 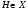 .
.
Доказательство. Возьмем произвольную подгруппу  из
из 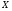 . Если
. Если  не нормальна в
не нормальна в  , то по теореме 1.4 найдется такой элемент
, то по теореме 1.4 найдется такой элемент 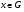 , что
, что  ,
,  ,
, 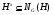 . По условиям 1) и 2)
. По условиям 1) и 2) 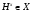 ,
, 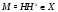 . Если
. Если  не нормальна в
не нормальна в  , то найдется
, то найдется 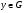 такой, что
такой, что 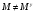 ,
,  ,
, 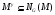 . Тогда
. Тогда 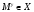 и
и 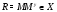 . Если
. Если 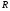 не нормальна, то описанную процедуру применяем к
не нормальна, то описанную процедуру применяем к 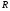 . Так как
. Так как  конечна, то этот процесс завершится построением нормальной подгруппы
конечна, то этот процесс завершится построением нормальной подгруппы 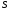 , представимой в виде
, представимой в виде  , где
, где  – некоторые элементы из
– некоторые элементы из  . Очевидно,
. Очевидно, 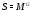 , и теорема доказана.
, и теорема доказана.
Следствие. Если  – непустой радикальный класс, то
– непустой радикальный класс, то 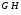 содержит все субнормальные
содержит все субнормальные  -подгруппы группы
-подгруппы группы  .
.
Доказательство. Пусть 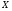 – множество всех субнормальных
– множество всех субнормальных  -подгрупп из
-подгрупп из  . Ввиду теоремы 1.12 легко заметить, что
. Ввиду теоремы 1.12 легко заметить, что 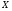 удовлетворяет условиям 1) и 2) теоремы 1.13.
удовлетворяет условиям 1) и 2) теоремы 1.13.
Следствие. Для любой субнормальной подгруппы  группы
группы  справедливы следующие утверждения:
справедливы следующие утверждения:
1) если  –
– 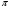 -группа, то
-группа, то 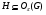 ;
;
2) если  нильпотентна, то
нильпотентна, то 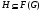 ;
;
3) если 
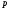 -нильпотентна, то
-нильпотентна, то 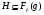 ;
;
4) если  разрешима, то
разрешима, то 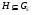 .
.
2. Минимальные не  -группы
-группы
Лемма [3]. Пусть 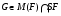 , где
, где  – локальная формация. Тогда справедливы следующие утверждения:
– локальная формация. Тогда справедливы следующие утверждения:
1) группа 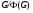 монолитична с монолитом
монолитична с монолитом
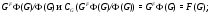
2)  –
– 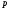 -группа для некоторого простого
-группа для некоторого простого 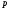 ;
;
3) 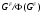 –
–  -эксцентральный главный фактор
-эксцентральный главный фактор  ;
;
4) 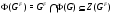 ;
;
5) если группа  неабелева, то ее центр, коммутант и подгруппы Фраттини совпадают и имеют экспоненту
неабелева, то ее центр, коммутант и подгруппы Фраттини совпадают и имеют экспоненту 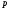 ;
;
6) если  абелева, то она элементарна;
абелева, то она элементарна;
7) если 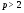 , то
, то 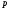 – экспонента
– экспонента  ; при
; при 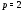 экспонента
экспонента  не превышает 4;
не превышает 4;
8) для любой  -абнормальной максимальной подгруппы
-абнормальной максимальной подгруппы  из
из  имеет место
имеет место
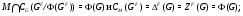
9) любые две  -абнормальные максимальные подгруппы группы
-абнормальные максимальные подгруппы группы  сопряжены в
сопряжены в  ;
;
10) если  и подгруппа
и подгруппа  содержит
содержит  , то
, то 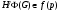 для любого полного локального экрана
для любого полного локального экрана  формации
формации  ;
;
11) если  –
–  -абнормальная максимальная подгруппа группы
-абнормальная максимальная подгруппа группы  и
и  – некоторый полный локальный экран
– некоторый полный локальный экран  , то
, то 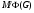 – минимальная не
– минимальная не 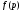 -группа и либо
-группа и либо 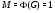 , либо
, либо  .
.
Доказательство. 1) Пусть 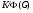 – минимальная нормальная подгруппа из
– минимальная нормальная подгруппа из 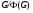 такая, что
такая, что 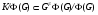 . Очевидно, что
. Очевидно, что 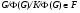 . Противоречие. Итак,
. Противоречие. Итак, 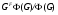 – минимальная нормальная подгруппа
– минимальная нормальная подгруппа 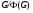 . Так как
. Так как  – формация, то, нетрудно заметить, что
– формация, то, нетрудно заметить, что 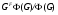 – единственная минимальная нормальная подгруппа из
– единственная минимальная нормальная подгруппа из 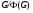 . А это значит, что
. А это значит, что
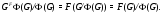
Отсюда следует, что
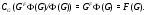
2) Выше мы показали, что 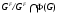 – главный
– главный  -фактор. Покажем, что
-фактор. Покажем, что  –
–  -группа. Предположим противное. Пусть простое число
-группа. Предположим противное. Пусть простое число 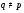 делит
делит  , но не делит
, но не делит 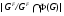 . По лемме 4.4 из [5]
. По лемме 4.4 из [5] 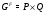 , где
, где 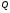 – содержащаяся в
– содержащаяся в 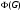 силовская
силовская 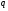 -подгруппа из
-подгруппа из  . Тогда
. Тогда
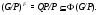
Отсюда и из насыщенности  получим
получим  . Но тогда
. Но тогда 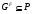 , что невозможно.
, что невозможно.
Пусть 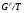 – главный фактор группы
– главный фактор группы  . Ввиду 2)
. Ввиду 2)  является
является 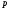 -группой и
-группой и 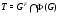 . Следовательно, каждая
. Следовательно, каждая  -абнормальная масимальная подгруппа группы
-абнормальная масимальная подгруппа группы  является
является  -нормализатором группы
-нормализатором группы  . Так как
. Так как  -нормализатор группы
-нормализатор группы  покрывает только
покрывает только  -центральные главные факторы, то мы получаем, что
-центральные главные факторы, то мы получаем, что 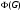
 -гиперцентральна в
-гиперцентральна в  . Согласно следствию 9.3.1 из [5]
. Согласно следствию 9.3.1 из [5] 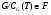 . Отсюда следует, что
. Отсюда следует, что 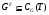 , т.е.
, т.е. 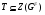 .
.
Обозначим через  коммутант группы
коммутант группы  . Так как
. Так как  –
–  -корадикал группы
-корадикал группы 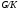 , то по теореме 11.6 из [5] каждый главный фактор группы
, то по теореме 11.6 из [5] каждый главный фактор группы  на участке от
на участке от  до
до 
 -эксцентрален. Отсюда и из
-эксцентрален. Отсюда и из  -гиперцентральности
-гиперцентральности  заключаем, что
заключаем, что 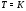 . Так как
. Так как
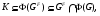
то мы получаем тaкже рaвенство  . Таким образом, утверждения 2) – 6), 9) доказаны.
. Таким образом, утверждения 2) – 6), 9) доказаны.
Докажем 7). Предположим, что  неабелева. Пусть
неабелева. Пусть 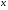 – произвольный элемент из
– произвольный элемент из  . Ввиду 4)
. Ввиду 4) 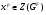 , причем
, причем 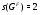 . Следовательно,
. Следовательно,

для всех элементов 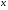 ,
,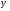 из
из  . Это означает, что
. Это означает, что  имеет экспоненту
имеет экспоненту 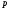 . Учитывая это и то, что
. Учитывая это и то, что 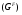 содержится в
содержится в 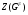 , получаем для любых
, получаем для любых 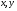 , из
, из  при
при 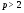 :
:
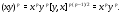
Значит, отображение  является
является  -эндоморфизмом группы
-эндоморфизмом группы  . Так как
. Так как
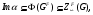
то 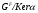
 -гиперцентральна в
-гиперцентральна в 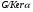 . Вспоминая, что
. Вспоминая, что 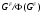 –
–  -эксцентральный главный фактор, получаем равенство
-эксцентральный главный фактор, получаем равенство  . Так как
. Так как 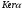 имеет экспоненту
имеет экспоненту 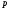 , то утверждение 7) при
, то утверждение 7) при 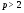 доказано.
доказано.
Пусть 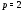 . Тогда
. Тогда
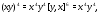
где  . Рассматривая отображение
. Рассматривая отображение  как и выше получаем, что
как и выше получаем, что 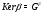 . Значит
. Значит  имеет экспоненту не больше 4.
имеет экспоненту не больше 4.
Докажем 8). Выше мы доказали, что  . Пусть
. Пусть  . Тогда в
. Тогда в  найдется такая максимальная подгруппа
найдется такая максимальная подгруппа  , что
, что  . Так как
. Так как 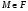 , то
, то 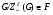 . Отсюда
. Отсюда 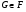 . Противоречие. Итак,
. Противоречие. Итак, 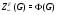 . По теореме 9.4 из [5] имеем
. По теореме 9.4 из [5] имеем 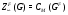 для любой
для любой  -абнормальной максимальной подгруппы
-абнормальной максимальной подгруппы  группы
группы  . Нетрудно показать, что
. Нетрудно показать, что 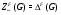 .
.
По теореме 7.11 из [5],
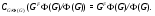
Так как 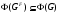 , то
, то

Ввиду того, что 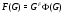 и
и 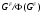 – главный фактор
– главный фактор  , имеем
, имеем  . Итак,
. Итак, 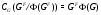 . Пусть
. Пусть  – любая
– любая  -абнормальная максимальная подгруппа группы
-абнормальная максимальная подгруппа группы  . Тогда
. Тогда 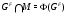 . Ясно, что
. Ясно, что
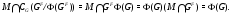
Не ограничивая общности, положим 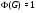 . Тогда
. Тогда  – единственная минимальная нормальная подгруппа
– единственная минимальная нормальная подгруппа  . Легко видеть, что
. Легко видеть, что 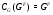 и
и 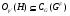 . Но
. Но  –
– 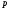 -группа. Значит,
-группа. Значит, 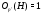 . По условию
. По условию 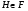 . Следовательно, ввиду полноты экрана
. Следовательно, ввиду полноты экрана  имеет место
имеет место
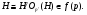
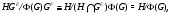
то 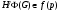 . Таким образом, всякая собственная подгруппа группы
. Таким образом, всякая собственная подгруппа группы 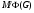 принадлежит
принадлежит 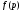 . Допустим, что
. Допустим, что 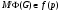 . Тогда
. Тогда
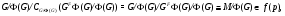
и поэтому 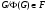 . Полученное противоречие показывает, что
. Полученное противоречие показывает, что 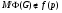 , т.е.
, т.е. 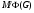 – минимальная не
– минимальная не 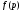 -группа.
-группа.
Предположим теперь, что  . Покажем, что
. Покажем, что 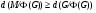 . Не теряя общности, можно положить, что
. Не теряя общности, можно положить, что 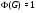 . Тогда
. Тогда 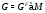 ,
, 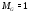 . Пусть
. Пусть 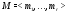 , где
, где 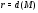 и
и 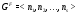 , где
, где 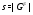 . Для всякого
. Для всякого 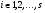 через
через 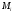 обозначим подгруппу
обозначим подгруппу  . Предположим, что все
. Предположим, что все 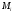 отличны от
отличны от  . Так как
. Так как 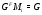 , то
, то 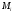 – дополнение к
– дополнение к  в
в  . Если
. Если  для всех различных
для всех различных 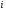 и
и 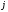 , то
, то
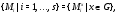
и поэтому 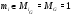 . Противоречие. Значит
. Противоречие. Значит 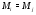 для некоторых различных
для некоторых различных 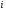 и
и 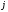 . Из последнего вытекает
. Из последнего вытекает

что невозможно. Полученное противоречие показывает, что 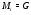 для некоторого
для некоторого 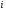 и, следовательно,
и, следовательно, 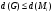 . Лемма доказана.
. Лемма доказана.
Лемма [4]. Пусть  – наследственная локальная формация,
– наследственная локальная формация, 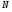 – такая нормальная подгруппа группы
– такая нормальная подгруппа группы  , что
, что 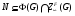 . Тогда
. Тогда  равносильно
равносильно 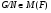 .
.
Доказательство. Пусть  . Тогда
. Тогда 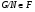 , и если
, и если  – произвольная максимальная подгруппа
– произвольная максимальная подгруппа  , то
, то  , а значит, и
, а значит, и 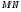 принадлежит
принадлежит  . Следовательно,
. Следовательно, 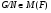 .
.
Предположим теперь, что 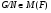 . Понятно, что
. Понятно, что 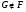 .Пусть
.Пусть  – произвольная максимальная подгруппа
– произвольная максимальная подгруппа  , тогда
, тогда 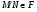 . Пусть
. Пусть  – произвольный
– произвольный  -главный фактор из
-главный фактор из 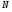 . Обозначим
. Обозначим 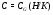 . Пусть
. Пусть  – максимальный внутренний локальный экран формации
– максимальный внутренний локальный экран формации  , и пусть
, и пусть 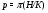 . Так как
. Так как 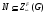 , то
, то  . Покажем, что
. Покажем, что  . По лемме 8.7 из [6] формация
. По лемме 8.7 из [6] формация 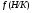 наследственна. Следовательно, если
наследственна. Следовательно, если 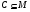 , то сразу получим
, то сразу получим 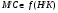 . Если же
. Если же 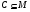 , то
, то  вытекает из изоморфизма
вытекает из изоморфизма 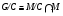 . Итак, всякий
. Итак, всякий  -главный фактор из
-главный фактор из 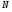 ,
,  -централен в
-централен в  . Значит,
. Значит, 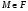 . Таким образом,
. Таким образом,  . Лемма доказана.
. Лемма доказана.
Лемма [3]. Пусть  – локальная наследственная формация,
– локальная наследственная формация,  – некоторый ее полный экран. Группа
– некоторый ее полный экран. Группа  принадлежит
принадлежит 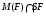 тогда и только тогда, когда выполняются следующие два условия:
тогда и только тогда, когда выполняются следующие два условия:
1) 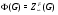 ;
;
2) 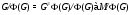 , где
, где 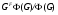 – главный
– главный 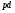 -фактор группы
-фактор группы  ,
, 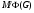 – минимальная не
– минимальная не 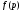 -группа.
-группа.
Доказательство. Необходимость вытекает из леммы 2.1.
Достаточность. Пусть 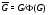 и
и 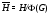 – произвольные максимальные подгруппы
– произвольные максимальные подгруппы 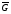 . Покажем, что
. Покажем, что 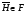 . Если
. Если 
 -абнормальна, то ввиду леммы 2.1 имеем
-абнормальна, то ввиду леммы 2.1 имеем 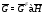 . Значит,
. Значит, 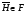 . Пусть
. Пусть 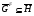 . По условию
. По условию
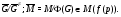
Следовательно, 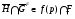 и по лемме 2.1
и по лемме 2.1  –
– 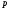 -группа. Значит по лемме 8.2 из [6]
-группа. Значит по лемме 8.2 из [6] 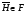 . Итак,
. Итак, 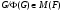 . Применяя теперь лемму 2.1 получаем, что
. Применяя теперь лемму 2.1 получаем, что  . Лемма доказана.
. Лемма доказана.
Лемма [3]. Пусть  – локальная формация, имеющая постоянный наследственный локальный экран
– локальная формация, имеющая постоянный наследственный локальный экран  . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения:
1) 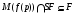 для любого
для любого 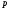 из
из  ;
;
2) 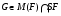 тогда и только тогда, когда
тогда и только тогда, когда 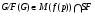 для любого
для любого 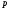 из
из  ,
, 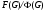 – главный
– главный 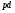 фактор
фактор  ,
, 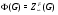 .
.
Доказательство. 1) Пусть  – произвольная группа из
– произвольная группа из 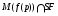 . Покажем, что
. Покажем, что 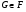 . Предположим противное. Пусть
. Предположим противное. Пусть  – подгруппа наименьшего порядка из
– подгруппа наименьшего порядка из  , не принадлежащая
, не принадлежащая  . Очевидно, что
. Очевидно, что 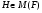 . Так как
. Так как  – постоянный экран, то ввиду леммы 4.5 из [5]
– постоянный экран, то ввиду леммы 4.5 из [5] 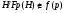 для любого
для любого 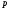 из
из  . Если
. Если 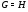 , то из того, что
, то из того, что 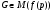 следует
следует 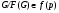 . Получили противоречие. Итак,
. Получили противоречие. Итак,  – собственная подгруппа из
– собственная подгруппа из  . Но тогда
. Но тогда 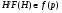 , что невозможно.
, что невозможно.
2) Пусть 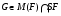 . Покажем, что
. Покажем, что  . Так как
. Так как
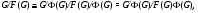
то, не ограничивая общности, можно считать, что 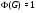 . Пусть
. Пусть  – произвольная
– произвольная  -абнормальная максимальная подгруппа группы
-абнормальная максимальная подгруппа группы  . Тогда по лемме 2.1
. Тогда по лемме 2.1 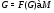 , где
, где  . Очевидно, что
. Очевидно, что 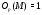 . Отсюда следует, что
. Отсюда следует, что 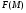 –
– 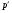 -группа. Так как
-группа. Так как 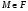 и
и  – постоянный экран, то
– постоянный экран, то  . Пусть
. Пусть  – произвольная собственная подгруппа из
– произвольная собственная подгруппа из  . Так как формация
. Так как формация 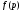 наследственна, то
наследственна, то 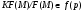 . Кроме того,
. Кроме того, 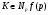 . Отсюда
. Отсюда 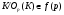 . Следовательно,
. Следовательно,
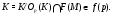
Если теперь 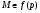 , то
, то 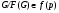 . Отсюда нетрудно заметить, что
. Отсюда нетрудно заметить, что 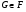 . Противоречие. Итак,
. Противоречие. Итак, 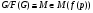 . Из леммы 2.1 следует, что
. Из леммы 2.1 следует, что
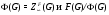
есть главный 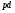 -фактор группы
-фактор группы  .
.
Пусть теперь 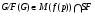 . Очевидно, что
. Очевидно, что 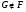 . Пусть
. Пусть  – собственная подгруппа из
– собственная подгруппа из  .Рассмотрим подгруппу
.Рассмотрим подгруппу 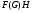 . Если
. Если 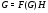 , то тогда
, то тогда
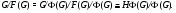
Согласно пункту 1  . Пусть
. Пусть 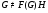 . Тогда
. Тогда 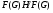 – собственная подгруппа группы
– собственная подгруппа группы 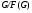 . Тогда
. Тогда

Отсюда 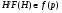 . А это значит, что
. А это значит, что 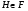 . Итак,
. Итак, 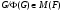 . Так как
. Так как 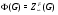 , то по лемме 2.1
, то по лемме 2.1  . Лемма доказана.
. Лемма доказана.
Лемма. Пусть  – непустая наследственная формация. Тогда:
– непустая наследственная формация. Тогда:
1) если  – подгруппа группы
– подгруппа группы  и
и 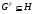 , то
, то 
 -субнормальна в
-субнормальна в  ;
;
2) если 
 -субнормальна в
-субнормальна в  ,
,  – подгруппа группы
– подгруппа группы  , то
, то 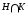
 -субнормальна в
-субнормальна в  ;
;
3) если 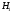 и
и 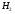
 -субнормальные подгруппы
-субнормальные подгруппы  , то
, то 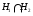 –
–  -субнормальная подгруппа
-субнормальная подгруппа  ;
;
4) если 
 -субнормальна в
-субнормальна в  , а
, а 
 -субнормальна в
-субнормальна в  , то
, то 
 -субнормальна в
-субнормальна в  ;
;
5) если все композиционные факторы группы  принадлежат формации
принадлежат формации  , то каждая субнормальная подгруппа группы
, то каждая субнормальная подгруппа группы  является
является  -субнормальной;
-субнормальной;
6) если  –
–  -субнормальная подгруппа группы
-субнормальная подгруппа группы  , то
, то 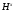
 -субнормальна в
-субнормальна в  для любых
для любых 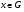 .
.
Лемма. Пусть  – непустая формация,
– непустая формация,  – подгруппа группы
– подгруппа группы  ,
, 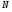 – нормальная подгруппа из
– нормальная подгруппа из  . Тогда:
. Тогда:
1) если 
 -субнормальна в
-субнормальна в  , то
, то 
 -субнормальна в
-субнормальна в  и
и 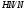
 -субнормальна в
-субнормальна в 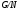 ;
;
2) если 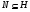 , то
, то 
 -субнормальна в
-субнормальна в  тогда и только тогда, когда
тогда и только тогда, когда 
 -субнормальна в
-субнормальна в 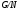 .
.
3. Формации с решеточным свойством
Лемма [1]. Пусть  – наследственная формация. Тогда следующие утверждения эквивалентны:
– наследственная формация. Тогда следующие утверждения эквивалентны:
1)  обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп;
-субнормальных подгрупп;
2) группа  принадлежит
принадлежит  , если
, если 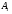 ,
, 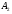 –
–  -субнормальные
-субнормальные  -подгруппы группы
-подгруппы группы  ;
;
3)  – формация Фиттинга и всякая
– формация Фиттинга и всякая  -субнормальная
-субнормальная  -подгруппа группы
-подгруппа группы  содержится в
содержится в  -радикале этой группы.
-радикале этой группы.
Установим, что из 1) следует 2).
Пусть  – контрпример минимального порядка. В этом случае
– контрпример минимального порядка. В этом случае  , где
, где 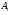
 -субнормальная
-субнормальная  -подгруппа группы
-подгруппа группы  ,
, 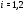 , и
, и  не принадлежит
не принадлежит  . Пусть
. Пусть 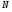 – минимальная нормальная подгруппа группы
– минимальная нормальная подгруппа группы  . Все условия леммы для фактор-групп выполняются, поэтому в силу выбора
. Все условия леммы для фактор-групп выполняются, поэтому в силу выбора  имеем, что
имеем, что 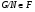 . В виду теоремы 4.3 из [7] формация
. В виду теоремы 4.3 из [7] формация  является насыщенной. Поэтому группа
является насыщенной. Поэтому группа  имеет единственную минимальную нормальную подгруппу
имеет единственную минимальную нормальную подгруппу 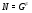 и
и 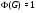 .
.
Если  , то
, то  – простая группа. Так как
– простая группа. Так как 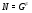 и
и 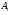 –
–  -субнормальная подгруппа группы
-субнормальная подгруппа группы  ,
,  , то либо
, то либо 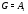 , либо
, либо 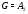 . Значит,
. Значит, 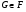 . Противоречие с выбором группы
. Противоречие с выбором группы  .
.
Пусть 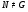 . Рассмотрим подгруппы
. Рассмотрим подгруппы 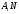 и
и 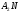 . Так как
. Так как 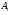 – собственная
– собственная  -субнормальная подгруппа
-субнормальная подгруппа  и
и 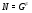 , то нетрудно видеть, что
, то нетрудно видеть, что 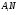 – собственная подгруппа
– собственная подгруппа  ,
, 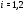 . Покажем, что
. Покажем, что 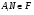 .
.
Рассмотрим два случая.
1. Пусть 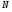 – абелева группа. Тогда
– абелева группа. Тогда 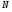 –
– 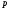 -группа,
-группа, 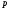 – простое число. Так как
– простое число. Так как  и подгруппа
и подгруппа 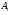
 -субнормальна в
-субнормальна в  , то по лемме 2.6 получаем
, то по лемме 2.6 получаем 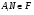 ,
,  .
.
2. Пусть 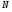 – неабелева группа. В этом случае
– неабелева группа. В этом случае

есть прямое произведение изоморфных неабелевых простых групп и 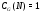 .
.
Рассмотрим подгруппу 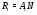 . Так как подгруппа
. Так как подгруппа 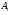
 -субнормальна в
-субнормальна в  , то ввиду леммы 2.4 и подгруппа
, то ввиду леммы 2.4 и подгруппа 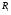
 -субнормальна в группе
-субнормальна в группе  . Пусть
. Пусть

Ввиду леммы 2.5 подгруппа 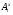
 -субнормальна в
-субнормальна в  для любого
для любого 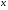 из
из 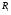 . Так как формация
. Так как формация  обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп, то
-субнормальных подгрупп, то 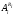 –
–  -субнормальная подгруппа
-субнормальная подгруппа 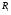 . Кроме того, из
. Кроме того, из 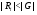 следует, что
следует, что 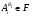 . Если
. Если  , то
, то  . Получили противоречие с
. Получили противоречие с 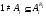 . Значит,
. Значит, 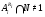 . Так как
. Так как 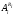 нормальна в
нормальна в 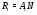 , то
, то 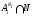 нормальна в
нормальна в 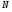 . Но
. Но
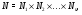
где 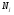 – неабелева простая группа и
– неабелева простая группа и 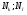 для всех
для всех 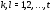 . Поэтому
. Поэтому
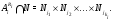
Из 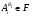 и наследственности формации
и наследственности формации  следует, что
следует, что 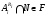 . Но тогда
. Но тогда 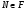 . Далее, так как
. Далее, так как 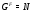 , то по лемме 2.5 подгруппа
, то по лемме 2.5 подгруппа 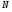
 -субнормальна в
-субнормальна в  . Значит, она
. Значит, она  -субнормальна и в
-субнормальна и в 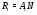 ,
, 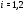 . Тогда из
. Тогда из 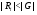 получаем что
получаем что
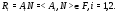
Пусть  – добавление к подгруппе
– добавление к подгруппе 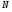 в группе
в группе  . Так как
. Так как 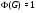 , то
, то  . В силу насыщенности формации
. В силу насыщенности формации  из
из
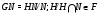
и
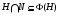
получаем, что 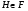 . Итак,
. Итак,  ,
, 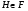 и
и 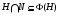 .
.
Используя тождество Дедекинда, имеем
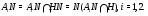
Если предположить, что 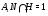 , то
, то 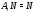 . В этом случае
. В этом случае
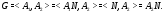
Так как 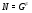 , то
, то 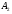 не может быть
не может быть  -субнормальной подгруппой в
-субнормальной подгруппой в  . Следовательно, можно считать, что
. Следовательно, можно считать, что  ,
, 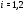 .
.
Так как подгруппа 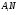
 -субнормальна в группе
-субнормальна в группе  и
и 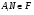 , то из наследственности формации
, то из наследственности формации  следует, что подгруппа
следует, что подгруппа 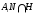
 -субнормальна в
-субнормальна в  .
.
Так как формация  обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп, то
-субнормальных подгрупп, то 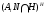 –
–  -субнормальная подгруппа группы
-субнормальная подгруппа группы  . Кроме того, из
. Кроме того, из 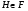 и наследственности формации
и наследственности формации  имеем
имеем 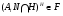 . Обозначим
. Обозначим  ,
, 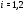 , и рассмотрим подгруппу
, и рассмотрим подгруппу 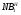 . Если
. Если 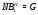 , то
, то 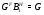 , что невозможно ввиду
, что невозможно ввиду  -субнормальности в
-субнормальности в  подгруппы
подгруппы 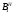 .
.
Пусть 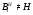 . Из
. Из  , нормальности
, нормальности 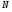 в
в  и нормальности
и нормальности 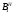 в
в  следует, что
следует, что 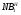 нормальна в
нормальна в  .
.
Так как

то
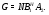
Таким образом получаем
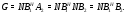
Так как  , то
, то  – подгруппа из
– подгруппа из  . Тогда из
. Тогда из  -субнормальности в
-субнормальности в  подгрупп
подгрупп 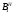 и
и 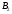 следует, что подгруппа
следует, что подгруппа
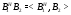
 -субнормальна в
-субнормальна в  . Это невозможно ввиду равенства
. Это невозможно ввиду равенства 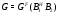 . Значит,
. Значит, 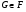 . Противоречие.
. Противоречие.
Докажем, что из 2) следует 3). Пусть  , где
, где 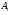 – нормальная
– нормальная  -подгруппа группы
-подгруппа группы  ,
, 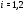 . Так как
. Так как
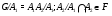
и 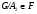 , то
, то 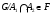 . Из наследственности формации
. Из наследственности формации  получаем, что подгруппа
получаем, что подгруппа 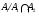
 -субнормальна в
-субнормальна в 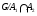 . Ввиду леммы 2.6 подгруппа
. Ввиду леммы 2.6 подгруппа 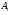 теперь
теперь  -субнормальна в
-субнормальна в  ,
, 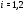 . Так как выполняется условие 2) леммы, то
. Так как выполняется условие 2) леммы, то
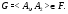
Следовательно,  – формация Фиттинга.
– формация Фиттинга.
Пусть 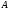 –
–  -субнормальная
-субнормальная  -подгруппа группы
-подгруппа группы  . Ввиду леммы 2.5 подгруппа
. Ввиду леммы 2.5 подгруппа 
 -субнормальна в
-субнормальна в 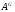 для всех
для всех 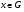 . Так как выполняются условия 2) леммы, то
. Так как выполняются условия 2) леммы, то

Отсюда следует, что
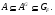
Наконец установим, что из 3) следует 1). Доказательство проведем индукцией по порядку группы  . Пусть
. Пусть  и
и  –
–  -субнормальные подгруппы группы
-субнормальные подгруппы группы  и
и 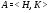 . Если
. Если 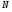 – минимальная нормальная подгруппа группы
– минимальная нормальная подгруппа группы  , то можно считать, что
, то можно считать, что 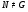 . Учитывая лемму 2.6 по индукции получаем, что
. Учитывая лемму 2.6 по индукции получаем, что 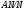 –
–  -субнормальная подгруппа группы
-субнормальная подгруппа группы 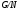 . На основании леммы 2.6 тогда подгруппа
. На основании леммы 2.6 тогда подгруппа 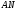
 -субнормальна в
-субнормальна в  . Если
. Если 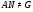 , то по индукции подгруппа
, то по индукции подгруппа 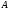
 -субнормальна в
-субнормальна в 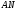 , и значит, ввиду леммы 2.5 она
, и значит, ввиду леммы 2.5 она  -субнормальна.
-субнормальна.
Будем далее считать, что  для любой минимальной нормальной подгруппы группы
для любой минимальной нормальной подгруппы группы  . Ясно, что
. Ясно, что 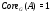 . Если
. Если 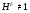 , то в силу леммы 3.1.3
, то в силу леммы 3.1.3 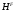 субнормальна в
субнормальна в  . Но тогда ввиду [8]
. Но тогда ввиду [8]
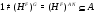
Это означает, что 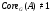 . Противоречие. Значит
. Противоречие. Значит 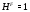 и
и 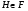 . Аналогично доказывается, что
. Аналогично доказывается, что 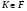 . Итак,
. Итак, 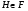 и
и 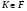 .
.
По условию леммы  – формация Фиттинга и
– формация Фиттинга и 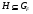 ,
, 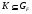 . Следовательно,
. Следовательно,
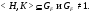
Пусть 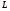 – минимальная нормальная подгруппа группы
– минимальная нормальная подгруппа группы  , содержащейся в
, содержащейся в 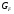 . Тогда
. Тогда
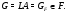
Из наследственности формации  следует, что
следует, что 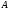 –
–  -субнормальная подгруппа группы
-субнормальная подгруппа группы  .
.
Итак, порождение двух  -субнормальных подгрупп
-субнормальных подгрупп  и
и  группы
группы 
 -субнормальна в
-субнормальна в  . Ввиду леммы 2.5
. Ввиду леммы 2.5 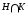 – также
– также  -субнормальная подгруппа группы
-субнормальная подгруппа группы  . Значит, формация
. Значит, формация  обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп. Лемма доказана.
-субнормальных подгрупп. Лемма доказана.
Лемма [1]. Пусть  – наследственная локальная формация. Если
– наследственная локальная формация. Если  замкнута относительно расширений, то формация
замкнута относительно расширений, то формация  обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп.
-субнормальных подгрупп.
Доказательство леммы следует из теоремы 5 работы [9] и теоремы 3.1.7.
Отметим, что из леммы 3.2 следует, что формации 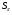 и
и 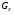 обладают решеточным свойством для
обладают решеточным свойством для  -субнормальных подгрупп.
-субнормальных подгрупп.
Пусть  обозначают некоторое подмножество множества натуральных чисел. Пусть
обозначают некоторое подмножество множества натуральных чисел. Пусть 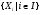 – некоторое семейство классов групп. Обозначим через
– некоторое семейство классов групп. Обозначим через 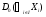 класс всех групп
класс всех групп  , представимых в виде
, представимых в виде
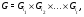
где 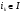 и
и 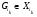 ,
, 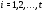 .
.
Лемма [1]. Справедливы следующие утверждения:
1) пусть 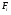 – наследственная локальная формация, обладающая решеточным свойством для
– наследственная локальная формация, обладающая решеточным свойством для 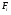 -субнормальных подгрупп,
-субнормальных подгрупп, 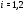 . Тогда и формация
. Тогда и формация 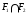 обладает решеточным свойством для
обладает решеточным свойством для 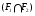 -субнормальных подгрупп;
-субнормальных подгрупп;
2) пусть 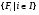 – некоторое семейство наследственных локальных формаций и
– некоторое семейство наследственных локальных формаций и 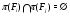 для любых
для любых 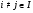 . Тогда и только тогда формация
. Тогда и только тогда формация

обладает решеточным свойством для  -субнормальных подгрупп, когда для каждого
-субнормальных подгрупп, когда для каждого 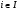 формация
формация 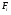 обладает решеточным свойством для
обладает решеточным свойством для 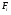 -субнормальных подгрупп.
-субнормальных подгрупп.
Пусть формация 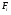 обладает решеточным свойством для
обладает решеточным свойством для 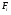 -субнормальных подгрупп,
-субнормальных подгрупп, 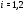 . Ввиду леммы 3.1
. Ввиду леммы 3.1 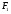 и
и 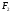 – формации Фиттинга поэтому из леммы 2.1.3 следует, что
– формации Фиттинга поэтому из леммы 2.1.3 следует, что 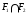 также является формацией Фиттинга.
также является формацией Фиттинга.
Пусть  –
– 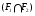 -субнормальная подгруппа группы
-субнормальная подгруппа группы  и
и 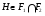 . Ясно, что подгруппа
. Ясно, что подгруппа 
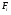 -субнормальна в
-субнормальна в  для любого
для любого 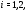 . Так как
. Так как  и
и 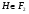 , то ввиду леммы 3.1 получаем, что
, то ввиду леммы 3.1 получаем, что 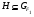 и
и  . Следовательно,
. Следовательно,

Теперь утверждение 1 следует из леммы 3.1.
Докажем утверждение 2). Пусть формация

обладает решеточным свойством для  -субнормальных подгрупп. Отметим, что
-субнормальных подгрупп. Отметим, что 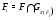 . Отсюда ввиду утверждения 1) настоящей леммы и леммы 3.2 следует, что формация
. Отсюда ввиду утверждения 1) настоящей леммы и леммы 3.2 следует, что формация 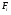 обладает решеточным свойством для
обладает решеточным свойством для 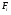 - субнормальных подгрупп.
- субнормальных подгрупп.
Обратно, пусть для любого 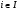 формация
формация 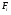 обладает решеточным свойством для
обладает решеточным свойством для 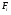 -субнормальных подгрупп. Пусть
-субнормальных подгрупп. Пусть
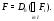
Индукцией по порядку группы  покажем, что любая группа
покажем, что любая группа 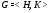 , где
, где  ,
,  –
–  -субнормальные
-субнормальные  -подгруппы группы
-подгруппы группы  принадлежат
принадлежат  .
.
Пусть 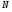 – минимальная нормальная подгруппа группы
– минимальная нормальная подгруппа группы  . Ввиду леммы 2.6 из соображений индукции получаем, что
. Ввиду леммы 2.6 из соображений индукции получаем, что 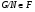 . Так как
. Так как  – насыщенная формация, то
– насыщенная формация, то  имеет единственную минимальную нормальную подгруппу
имеет единственную минимальную нормальную подгруппу 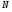 и
и 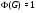 . Ясно, что
. Ясно, что
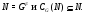
Отметим также, что
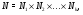
где  – изоморфные простые группы для
– изоморфные простые группы для  .
.
Докажем, что 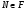 . Рассмотрим группу
. Рассмотрим группу 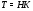 . Так как подгруппа
. Так как подгруппа 
 -субнормальна в
-субнормальна в  , то
, то 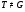 . Тогда по индукции
. Тогда по индукции
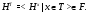
Рассмотрим пересечение 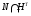 . Если
. Если
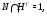
то

Отсюда и из того факта, что 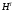 – нормальная подгруппа
– нормальная подгруппа  и
и  следует, что
следует, что 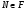 .
.
Пусть  . Так как
. Так как 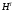 – нормальная подгруппа из
– нормальная подгруппа из 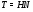 , то
, то  – нормальная подгруппа из
– нормальная подгруппа из 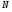 . А это значит, что
. А это значит, что
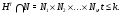
Из наследственности формации  и
и  получаем, что
получаем, что 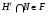 . Но тогда
. Но тогда 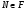 .
.
Из строения 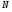 и
и
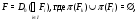
для любых 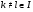 , следует, что
, следует, что 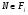 для некоторого
для некоторого 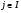 . Так как
. Так как
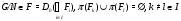
то нетрудно видеть, что группа  имеeт
имеeт 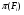 -холловскую подгруппу
-холловскую подгруппу 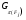 .
.
Так как 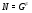 , то
, то 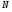 –
–  -субнормальная подгруппа группы
-субнормальная подгруппа группы  . Так как
. Так как 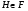 ,
, 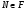 и
и  ,
,  –
–  -субнормальные подгруппы, то по индукции имеем, что
-субнормальные подгруппы, то по индукции имеем, что
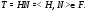
Отсюда и из 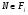 ввиду
ввиду 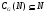 получаем
получаем  . Аналогично доказывается, что
. Аналогично доказывается, что 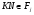 . Таким образом,
. Таким образом,
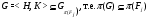
Отсюда и из  -субнормальности
-субнормальности  и
и  в
в  нетрудно заметить, что
нетрудно заметить, что  ,
,  –
–  -субнормальные подгруппы группы
-субнормальные подгруппы группы  . Из
. Из  и
и 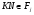 ввиду наследственности
ввиду наследственности 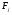 следует, что
следует, что 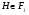 и
и 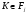 . Так как по условию формация
. Так как по условию формация 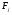 обладает решеточным свойством для
обладает решеточным свойством для 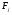 - субнормальных подгрупп, то ввиду леммы 3.1
- субнормальных подгрупп, то ввиду леммы 3.1
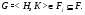
Итак,  содержит некоторую группу
содержит некоторую группу 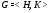 , где
, где  ,
,  –
–  -субнормальные
-субнормальные  -подгруппы группы
-подгруппы группы  . Следовательно, ввиду леммы 3.1 формация
. Следовательно, ввиду леммы 3.1 формация  обладает решеточным свойством для
обладает решеточным свойством для  -субнормальных подгрупп. Лемма доказана.
-субнормальных подгрупп. Лемма доказана.
Лемма [1]. Пусть  – нормально наследственная разрешимая формация. Тогда справедливы следующие утверждения:
– нормально наследственная разрешимая формация. Тогда справедливы следующие утверждения:
1) если в каждой разрешимой группе все  -субнормальные подгруппы образуют решетку, то
-субнормальные подгруппы образуют решетку, то  имеет вид
имеет вид

где 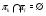 для любых
для любых 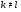 из
из  ;
;
2) если  – формация из пункта 1), то она обладает решеточным свойством для
– формация из пункта 1), то она обладает решеточным свойством для  -субнормальных подгрупп.
-субнормальных подгрупп.
1) Покажем, что 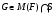 является либо группой Шмидта, либо группой простого порядка. Очевидно, что
является либо группой Шмидта, либо группой простого порядка. Очевидно, что 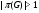 и
и 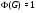 .
.
Пусть  – максимальный внутренний локальный экран формации
– максимальный внутренний локальный экран формации  . Согласно лемме 2.3
. Согласно лемме 2.3
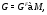
где  – единственная минимальная нормальная подгруппа группы
– единственная минимальная нормальная подгруппа группы  ,
, 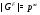 (
(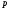 – простое число), а
– простое число), а  – максимальная подгруппа группы
– максимальная подгруппа группы  , являющейся минимальной не
, являющейся минимальной не 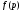 -группой.
-группой.
Докажем, что  – циклическая
– циклическая 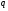 -группа для некоторого простого числа
-группа для некоторого простого числа 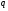 . Допустим противное. Тогда в
. Допустим противное. Тогда в  найдутся по крайней мере две несопряженные максимальные подгруппы
найдутся по крайней мере две несопряженные максимальные подгруппы 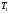 и
и  . Рассмотрим в
. Рассмотрим в  подгруппу
подгруппу 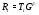 ,
, 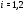 . Ясно, что
. Ясно, что 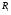
 -субнормальна в
-субнормальна в  ,
, 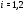 . Из
. Из  ,
, 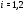 и
и  по лемме 3.1 получаем, что
по лемме 3.1 получаем, что 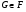 . Получили противоречие с выбором
. Получили противоречие с выбором  .
.
Следовательно,  – циклическая группа порядка
– циклическая группа порядка 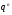 , где
, где 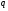 – некоторое простое число,
– некоторое простое число, 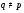 ,
, 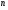 – натуральное число. Допустим, что
– натуральное число. Допустим, что 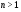 . Обозначим через
. Обозначим через 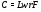 – регулярное сплетение циклических групп
– регулярное сплетение циклических групп 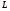 и
и  соответственно порядков
соответственно порядков 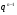 и
и 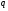 .
.
По теореме 6.2.8 из [2]  изоморфна некоторой подгруппе группы
изоморфна некоторой подгруппе группы  . Так как
. Так как 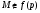 и
и 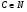 , то ввиду теоремы 2.4 из [5]
, то ввиду теоремы 2.4 из [5] 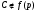 .
.
Рассмотрим регулярное сплетение 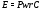 , где
, где  . Тогда
. Тогда 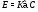 , где
, где  – элементарная абелева
– элементарная абелева 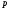 -группа. Так как
-группа. Так как 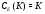 , то
, то 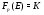 . Из
. Из
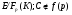
следует что 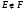 .
.
Рассмотрим в 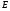 подгруппы
подгруппы 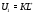 и
и 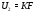 , где
, где 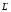 – база сплетения
– база сплетения 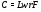 . Ясно, что
. Ясно, что 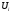
 -субнормальна в
-субнормальна в 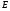 ,
, 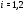 . Кроме того,
. Кроме того, 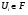 . Отсюда
. Отсюда
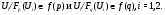
Так как 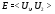 , то
, то 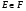 по лемме 3.1. Получили противоречие.
по лемме 3.1. Получили противоречие.
Следовательно,  и
и  – группа Шмидта. Если
– группа Шмидта. Если 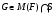 и
и 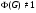 , то по лемме 1.1.6
, то по лемме 1.1.6  также является группой Шмидта. Таким образом, любая разрешимая минимальная не
также является группой Шмидта. Таким образом, любая разрешимая минимальная не  -группа является либо группой Шмидта, либо имеет простой порядок. Тогда по лемме 3.1.12
-группа является либо группой Шмидта, либо имеет простой порядок. Тогда по лемме 3.1.12  является наследственной формацией.
является наследственной формацией.
Покажем, что формация  имеет такой локальный экран
имеет такой локальный экран  , что
, что
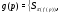
p(F)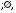 p'(F)
p'(F)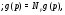 p(F)
p(F) Действительно. Пусть
Действительно. Пусть  – локальный экран формации
– локальный экран формации 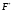 . Так как
. Так как  для любого простого числа
для любого простого числа 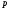 из
из  , то
, то 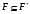 . Покажем обратное.
. Покажем обратное.
Пусть  – группа минимального порядка из
– группа минимального порядка из  . Так как
. Так как 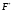 – наследственная формация и
– наследственная формация и  – насыщенная формация, то
– насыщенная формация, то  – минимальная не
– минимальная не  -группа и
-группа и 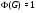 . Теперь, согласно лемме 2.3
. Теперь, согласно лемме 2.3
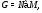
где 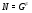 – единственная минимальная нормальная подгруппа группы
– единственная минимальная нормальная подгруппа группы  , причем
, причем 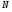 –
– 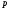 -группа,
-группа,  , а
, а  – минимальная не
– минимальная не 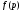 -группа. Как показано выше
-группа. Как показано выше  является либо группой простого порядка, либо группой Шмидта.
является либо группой простого порядка, либо группой Шмидта.
Пусть  – группа простого порядка. Так как
– группа простого порядка. Так как 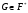 , то очевидно, что
, то очевидно, что 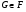 . Противоречие.
. Противоречие.
Пусть  – группа Шмидта. Тогда
– группа Шмидта. Тогда  – группа простого порядка, причем
– группа простого порядка, причем 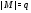 ,
, 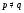 . Так как
. Так как 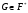 , то очевидно, что
, то очевидно, что

Отсюда следует, что 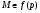 . Получили противоречие. Следовательно
. Получили противоречие. Следовательно 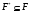 .
.
Итак,  и
и  – полный локальный экран формации
– полный локальный экран формации  .
.
Покажем, что 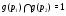 либо
либо 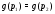 для любых простых
для любых простых  ,
,  .
.
Вначале докажем, что из 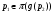 следует
следует 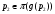 . Допустим противное. Пусть
. Допустим противное. Пусть  . Рассмотрим точный неприводимый
. Рассмотрим точный неприводимый 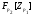 -модуль
-модуль  над полем
над полем 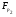 , который существует по лемме 18.8 из [6].
, который существует по лемме 18.8 из [6].
Возьмем группу 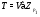 . Так как
. Так как 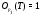 и
и  имеет единственную минимальную нормальную подгруппу, то ввиду леммы 18.8 из [6] существует точный неприводимый
имеет единственную минимальную нормальную подгруппу, то ввиду леммы 18.8 из [6] существует точный неприводимый 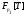 -модуль
-модуль 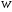 над полем
над полем 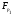 . Рассмотрим группу
. Рассмотрим группу
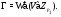
Так как
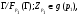
то 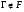 . Ясно, что
. Ясно, что 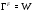 . Так как
. Так как 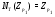 , то найдется
, то найдется 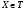 такой, что
такой, что  . Заметим, что
. Заметим, что  . Тогда
. Тогда
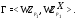
Так как 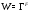 , то
, то 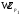
 -субнормальна в
-субнормальна в  и
и 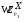
 -субнормальна в
-субнормальна в  . По лемме 3.1
. По лемме 3.1 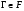 . Получили противоречие. Таким образом, если
. Получили противоречие. Таким образом, если 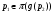 , то
, то 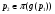 .
.
Пусть теперь 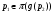 . Тогда
. Тогда 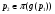 . Предположим, что найдется такое простое число
. Предположим, что найдется такое простое число 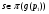 , которое не принадлежит
, которое не принадлежит 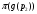 . Рассмотрим точный неприводимый
. Рассмотрим точный неприводимый 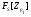 -модуль
-модуль 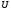 над полем
над полем  .
.
Группа 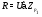 принадлежит
принадлежит  ввиду
ввиду 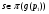 и
и  . Теперь рассмотрим точный неприводимый
. Теперь рассмотрим точный неприводимый 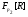 -модуль
-модуль 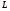 . Группа
. Группа 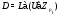 формации
формации  не принадлежит, так как
не принадлежит, так как  . Ясно, что
. Ясно, что  . Рассуждая как и выше, можно показать, что
. Рассуждая как и выше, можно показать, что  для некоторого
для некоторого 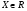 , причем подгруппы
, причем подгруппы 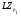 ,
, 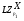
 -субнормальны в
-субнормальны в 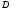 , причем
, причем 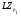 ,
, 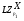 принадлежат
принадлежат  . Отсюда по лемме 3.1
. Отсюда по лемме 3.1 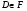 . Получили противоречие.
. Получили противоречие.
Следовательно, если 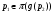 , то
, то 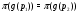 , а значит
, а значит 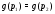 . Более того, если
. Более того, если
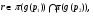
где 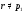 и
и  , то
, то  и
и 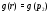 , а значит,
, а значит, 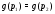 .
.
Таким образом, множество  можно разбить в объединение непересекающихся подмножеств, т.е. представить в виде
можно разбить в объединение непересекающихся подмножеств, т.е. представить в виде  , где
, где 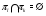 для любых
для любых 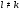 из
из  и
и 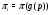 для
для  . Покажем, что
. Покажем, что
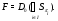
Обозначим
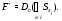
Так как для любого  имеет место
имеет место  , то включение
, то включение 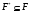 очевидно.
очевидно.
Допустим, что множество 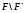 непусто, и выберем в нем группу
непусто, и выберем в нем группу  наименьшего порядка. Так как
наименьшего порядка. Так как  – наследственная формация, то
– наследственная формация, то 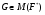 . Группа
. Группа  непримарна в силу равенства
непримарна в силу равенства 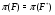 и локальности формации
и локальности формации 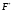 . Из строения
. Из строения
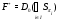
и 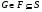 нетрудно показать, что
нетрудно показать, что  – группа Шмидта. Ясно, что
– группа Шмидта. Ясно, что 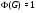 . Тогда по теореме 26.1 из [5]
. Тогда по теореме 26.1 из [5] 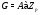 , где
, где 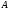 – элементарная абелева
– элементарная абелева 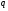 -группа,
-группа, 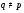 – некоторые простые числа. Так как
– некоторые простые числа. Так как 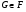 , то
, то
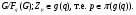
Как показано выше, 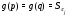 для некоторого номера
для некоторого номера 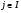 . Но тогда
. Но тогда 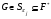 . Получили противоречие с выбором
. Получили противоречие с выбором  . Следовательно,
. Следовательно,

где 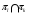 для всех
для всех 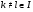 .
.
Утверждение 2) следует из лемм 3.2 и 3.3. Лемма доказана.
Из доказанной леммы следует, что разрешимая наследственная локальная формация  тогда и только тогда обладает решеточным свойством для
тогда и только тогда обладает решеточным свойством для  -субнормальных подгрупп, когда
-субнормальных подгрупп, когда

Заключение
В курсовой работе рассмотрены решетки субнормальных и  -субнормальных подгрупп. Для построения теории решеток
-субнормальных подгрупп. Для построения теории решеток  -субнормальных подгруп, аналогичной теории решеток субнормальных подгрупп, разработанной Виландтом, используются свойства минимальных не
-субнормальных подгруп, аналогичной теории решеток субнормальных подгрупп, разработанной Виландтом, используются свойства минимальных не  -групп.
-групп.
В работе рассматриваются условия, при выполнении которых формация будет обладать решеточным свойством.
Список использованных источников
1. Васильев А.Ф., Каморников С.Ф., Семенчук В.Н. О решетках подгрупп конечных групп // Бесконечные группы и примыкающие алгебраические структуры: Тр./ Институт математики АН Украины. – Киев, 1993. – С. 27–54.
2. Коуровская тетрадь (нерешенные вопросы теории групп). Новосибирск: Институт математики СО АН СССР, 1984. – 144 с.
3. Семенчук В.Н. Минимальные не  -группы // Алгебра и логика. – 1979. – Т.18, №3. – С. 348–382.
-группы // Алгебра и логика. – 1979. – Т.18, №3. – С. 348–382.
4. Семенчук В.Н. Конечные группы с системой минимальных не  -подгрупп // Подгрупповое строение конечных групп: Тр./ Ин-т математики АН БССР. – Минск: Наука и техника, 1981. – С. 138–149.
-подгрупп // Подгрупповое строение конечных групп: Тр./ Ин-т математики АН БССР. – Минск: Наука и техника, 1981. – С. 138–149.
5. Шеметков Л.А. Формации конечных групп. М.: Наука. – 1978. – 267 с.
6. Шеметков Л.А., Скиба А.Н. Формации алгебраических систем. М.: Наука. – 1989. – 256 с.
7. Bryce R.A., Cossey J. Fitting formations of finite solubla groups // Math.Z. – 1972. – V.127, №3. – P.217–233.
8. Gaschьtz W. Zur Theorie der endlichen auflцsbaren Gruppen. – Math. Z., 1963, 80, №4, С. 300–305.
9. Kegel O.H. Untergruppenverbande endlicher Gruppen, die Subnormalteilorverband echt enthalten // Arch. Math. – 1978. – V.30. – P.225–228.
10. Wielandt H. Eine Verallgemeinerung der invarianten Untegruppen // Math.Z. – 1939.-V.45. – P.209–244.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ