Схема Бернулли. Цепи Маркова

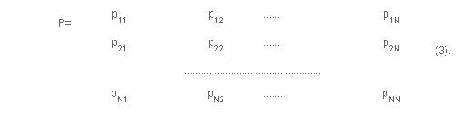


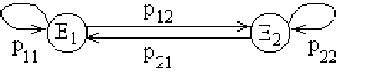
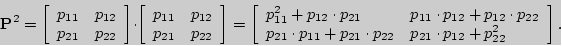
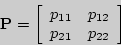
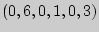
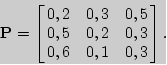

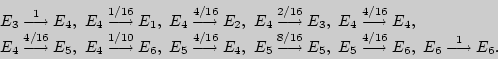
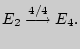
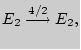
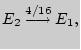
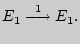
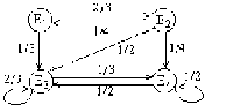

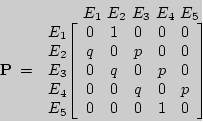
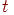
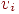
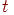
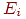
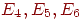
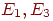
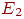
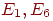
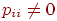
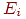
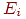
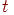
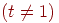
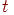
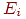
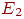
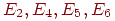
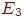
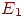
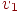
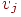
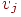
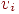
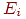
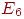
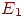
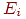
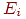
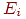
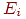
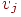
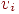
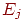
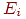
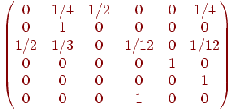

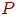
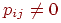
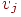
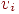
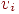
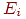
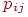
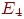
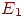
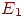
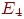
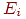
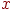
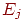
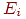
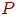
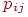
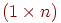
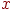
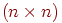
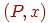
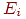
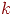
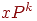
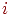
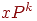
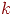
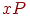
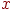
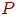
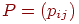
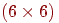
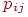
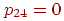
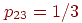
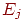
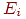
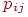
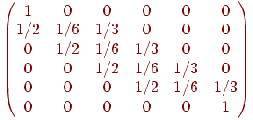
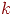
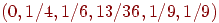
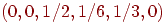
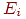
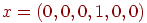
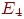
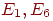
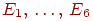

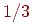
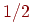
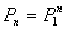
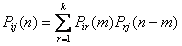
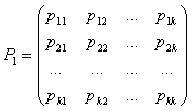
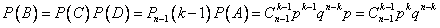
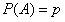
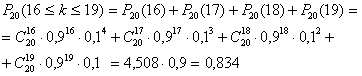
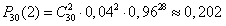
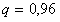
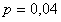
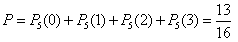
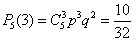
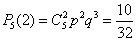

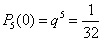
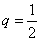
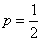
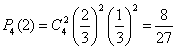
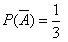
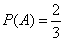
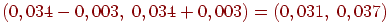

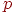
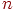
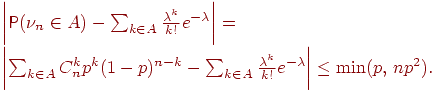
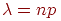
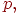
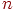
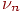
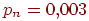
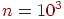
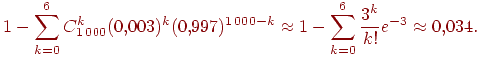
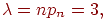
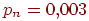
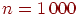

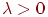
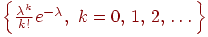
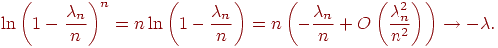
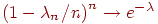

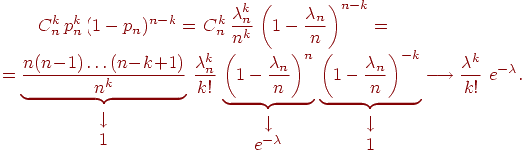

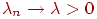
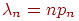
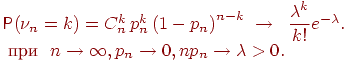
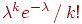
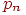
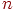
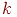
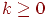
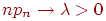
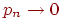
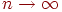
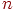
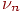
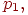
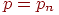
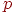
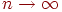
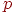
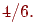
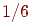
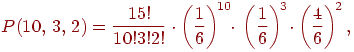
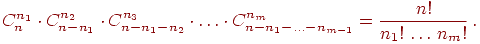
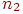
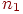
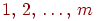
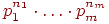
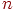
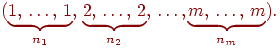
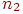
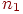
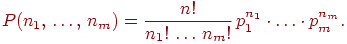
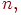
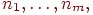
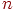
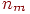
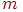
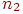
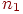
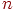
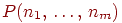

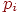
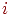
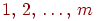
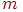
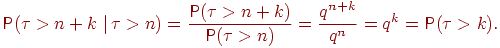
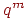
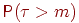
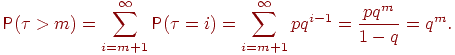
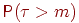
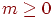
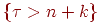
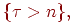
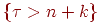
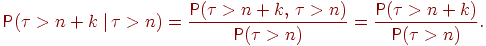

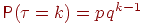
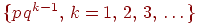

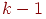
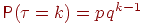
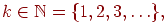
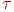
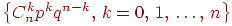
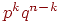
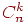
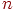
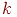
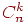
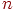
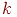
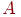
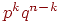
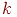

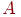
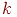
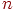
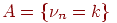
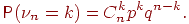
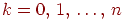
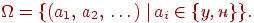
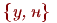
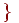
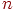
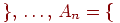
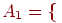
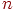
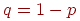
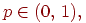 Введение
Введение
Цепь Маркова — последовательность случайных событий с конечным или счётным бесконечным числом исходов, характеризующаяся тем свойством, что при фиксированном настоящем будущее независимо от прошлого.
Цепи Маркова – одна из основных и актуальных тем в нынешнее время в современной математике. Цепи Маркова являются обобщением схемы Бернулли, которая была написана в XVII, а Марковские цепи получили сравнительно недавно свое признание. Очень много процессов в нынешнее время решаются с помощью схем Бернулли или цепей Маркова. Вся поисковая система Интернета основана на этих процессах.
Эта была одна из основных причин выбора мною этой темы для выпускной квалификационной работы (ВКР). Мне было очень интересно, по какому принципу происходит выборка по рассылке, или по поиску в Интернете. Рассылка спам-ботов основана тоже на этих же процессах.
Цель моей работы – Ознакомиться и как можно подробнее рассмотреть заинтересовавший меня материал. Особенно интересной для меня была эта тема по той причине, что она не рассматривалась в курсе моего обучения в институте, а является частью пройденного материала по теории вероятности.
Свою работу «Приложение схемы Бернулли. Обобщение. Цепи Маркова» я начинаю с введения понятий касающихся раздела схемы Бернулли. Из этого и состоят моя первая глава ВКР - Биография Якоба Бернулли и схема Бернулли. Я рассматриваю различные варианты схем Бернулли, как она по-разному применятся, различные формы записи, обобщения.
Во второй главе своей работы я уже по выше рассмотренным понятиям схем Бернулли ввожу понятие Цепь Маркова, которая была так названа в честь нашего соотечественника, великого математика, Андрея Андреевича Маркова. Для лучшего понятия темы Цепи Маркова в этой главе я рассматриваю введение понятия цепь Маркова с помощью примера.
Третья глава дает нам представление о том, какой объем работы может выполнять человек, который владеет цепями Маркова. Подробно рассматриваю на примере по определению авторства текста. Я посчитал этот пример очень удачным применением Цепей Маркова.
Глава 1. Схема Бернулли
1.1 Исторический курс. Биография Якоба Бернулли
Якоб Бернулли родился 27 декабря 1654 г. По желанию отца готовился к званию протестантского священника. Окончил Базельский университет, где изучал философию, богословие и языки. Владел немецким, французским, английским, итальянским, латинским и греческим языками. Испытывая непреодолимое влечение к математике, изучал ее тайком от отца. В 1671 г. получил степень магистра философии. С большим успехом читал проповеди на немецком и французском языках. В то же время продолжал пополнять свои знания по математике без учителя, почти без учебников.
В октябре 1686 г. оказывается вакантной должность профессора математики в Базельском университете. Успехи Якоба в математике хорошо известны, и Сенат университета единодушно выдвинул на вакантную должность Якоба Бернулли. Вступление в должность состоялось 15 февраля 1687 г. Вряд ли присутствовавшие при этом скромном акте представляли, что они являются свидетелями начала беспримерного в истории математики события: отныне кафедру будут занимать Бернулли на протяжении ста лет. Члены же этой семьи будут профессорами родного университета в течение четверти тысячелетия, вплоть до второй половины XX в.
В том же году Якоб Бернулли прочитал в «Асtа Eruditirum» за 1684 г. «Новый метод» Лейбница и, обнаружив трудные места, письменно обратился к Лейбницу за разъяснением. Лейбниц, находившийся в длительной служебной поездке, получил письмо только через три года, когда надобность в консультации отпала: Якоб совместно Иоганном овладели дифференциальным и интегральным исчислениями настолько, что вскоре смогли приступить систематическому развитию метода. Образовавшийся триумвират — Лейбниц, Якоб и Иоганн Бернулли — менее чем за двадцать лет чрезвычайно обогатил анализ бесконечно малых.
С 1677 г. Я. Бернулли стал вести записные книжки, куда вносил различного рода заметки научного содержания. Первые записи посвящены теологии, сделаны под влиянием распространенного в то время в Базеле сборника спорных теологических вопросов.
Основное место в записных книжках занимает решение задач. Уже по ранним записям можно судить о проявленном Я. Бернулли интересе к прикладной математике. Математические заметки показывают, как постепенно Я. Бернулли овладевал методами Валлиса, Декарта, инфинитезимальными методами, как развивал и совершенствовал их. Решенные им задачи служили отправными пунктами для дальнейших более глубоких исследований.
В январе 1684 г. Я. Бернулли провел в Базельском университете открытый диспут, на котором защищал 100 тезисов, из них 34 логических, 18 диалектических и 48 смешанных. Некоторые тезисы крайне любопытны. Вот примеры:
78. Иногда существует несколько кратчайших путей из точки в точку
83. Среди изопериметрических фигур одна может быть в бесконечное число раз больше другой
85. Не в каждом треугольнике сумма внутренних углов равна двум прямым
89. Квадратура круга еще не найдена, но не потому, что между искривленным и прямолинейным нет никакой связи; в действительности кривую можно спрямить, а криволинейную фигуру квадрировать
В мае 1690 г. Я. Бернулли опубликовал в «Асtа Eruditirum» первую работу, связанную с исчислением бесконечно малых. В ней он дал решение поставленной Лейбницем в 1687 г. задачи о парацентрической изохроне. Необходимо было найти кривую, по которой материальная точка опускалась бы в равные промежутки времени на равные высоты. Я. Бернулли вывел дифференциальное уравнение кривой и проинтегрировал его. При этом он впервые употребил в печати термин «интеграл», указав, что из равенства двух выражений, связывающих дифференциалы, следует равенство интегралов.
В лекциях, читанных Лопиталю, И. Бернулли ход решения излагает так. Пусть искомой кривой будет АDС. Материальная точка за время ∆t перемещается из точки D в точку d и из точки С в точку с. По условию задачи проекции дуг Dd Сс на вертикаль одинаковы. Проведем через D и С касательные к кривой до пересечения с продолжением АF. Отрезки касательных будут DK и CL. Напишем тождество
Вв.Сс=Вв.Рс • Рс.Ссю
Дуги Dd и Сс малы, поэтому фигуры GDd и НСс можно считать треугольниками.
Из подобия треугольников GDd и DEK, НСс и СFL получим
Вв.ВП=ВЛ.ВУбСс.Нс=СД.САю
С помощью этих пропорций найдем
Вв.Сс=ВП1Нс • ВК.ВЕ • СА.СДю
По условиям задачи dG/Нс=1, поэтому
Вв1Сс=ВК.ВЕ • СА.СДю
Проведем через точку С прямую СМ, параллельную DК. Тогда
DК/DЕ=СМ/СF, Dd/Сс=СМ/СL.
Но отношение Dd/Сс равно отношению скоростей (интервал ∆t один и тот же), квадраты же скоростей, по найденному Галилеем закону, относятся как пройденные высоты; это дает
Dd2/Сс2=СМ2/СL2=DЕ/CF, СМ2/СL2 =DЕ/СF.
Последнее равенство означает, что если через две произвольные точки кривой провести касательные СL и DК и через точку С провести СМ параллельно DК, то должна выполняться указанная пропорция. Таким свойством обладает искомая кривая.
Задача оказалась сведенной к классу обратных задач на касательные: найти кривую, касательные к которой удовлетворяют некоторому требованию. Подобную задачу впервые предложил Декарту Дебон, и Декарт с ней не справился. Разработанный Лейбницем метод позволяет решать и обратные задачи на касательные.
Выберем начало координат в точке А. Обозначим АЕ=х, ЕD=у. Тогда GD=dх, Gd=dу. Обозначим также СF=а, СL=b. Треугольники FСМ и СdD подобны, отсюда
Gd/Dd=FС/СМ.
Но Dd = √dx2+dy2, поэтому
dy/√ dx2+dy2= а/СМ, откуда
CM2= (a2dx2+a2dy2)/dy2.
Подставим найденное выражение в пропорцию СL2/СM2=СF/СЕ и получим дифференциальное уравнение
и2вн2.(ф2вч2+ф2вн2)=ф.нб и2нвн2-ф3вн2=ф3вч2б (и2н-а3)ву2 = а3вч2б
√b2y-a3 dy=√a3 dx.
В уравнении переменные разделены, интегрирование его дает искомую кривую
2b2у — 2а3/3b2 √b2у - а3 == х√а3.
Парацентрическая изохрона оказалась полукубической параболой. Вид кривой раньше Я. Бернулли определили Лейбниц и Гюйгенс, но лишь Я. Бернулли дал решение средствами анализа бесконечно малых.
В приложении к другой работе о рядах (1694 г.) Я. Бернулли сформулировал несколько тезисов.
1. Существуют спирали, которые совершают бесконечное число витков вокруг полюса, но имеют конечную длину.
2. Существуют кривые, которые, подобно эллипсу, замкнуты и, подобно параболе, уходят в бесконечность, например ay2=х2(b+х).
3. Существуют кривые, состоящие из двух ветвей, например ау2=х(а2—х2),
4. Существуют неограниченные поверхности с конечной площадью.
5. Существуют неограниченные поверхности с бесконечной площадью, но такие, что соответствующие им тела вращения обладают конечным объемом.
Я. Бернулли увлекался также и изопериметрическими задачами. Древнейшая из них—задача легендарной основательницы Карфагена и его первой царицы Дидоны. Легенда такова. Дидона бежала от отца, тирского царя, и достигла Африки, где купила у туземцев участок земли на берегу моря «не больше, чем можно окружить воловьей шкурой». Она разрезала шкуру на узкие полоски и связала из них длинную ленту. Спрашивается, какой формы должна быть фигура, оцепленная лентой данной длины, чтобы площадь фигуры была наибольшей?
Ван-дер-Варден пишет, что Зенодор, живший вскоре после Архимеда, высказал 14 предложений относительно изопериметрических фигур. Он утверждал, что из всех фигур (кругов и многоугольников), имеющих одинаковый периметр, круг будет наибольшим, а также и то, что из всех пространственных тел с одинаковой поверхностью наибольшим будет шар.
Решение задачи содержится в записных книжках Я. Бернулли и помещено в майском номере «Acta Eruditorum» за 1701 г. Я. Бернулли и здесь применил высказанный ранее принцип: поскольку площадь должна быть экстремальной, этим же свойством должна обладать и любая ее элементарная часть. Он получил дифференциальное уравнение третьего порядка и впоследствии проинтегрировал его.
К.А. Рыбников пишет: «Таким образом, решение изопериметрической задачи означало очень важный, принципиально новый этап в истории вариационного исчисления; оно дало возможность решать более сложные вариационные задачи, им был сделан важный шаг на пути решения вариационных задач».
При изучении свойств сочетаний и фигурных чисел Я. Бернулли встретился с суммированием степеней натуральных чисел Sm = å km
Эти вопросы интересовали математиков и ранее. Я. Бернулли составил таблицу фигурных чисел, указал их свойства и на основании отмеченных свойств нашел формулы для сумм степеней натуральных чисел. Он привел формулы сумм от S(n) до S(n10):
S (n) = n2/2 +n/2
S (n2) = n3/3 + n2/2+ n/6
S (n3) = n4/4 + n3/2 + n2/4
S (n4) = n5/5 + n4/2 + n3/3 – n/30
S (n5) = n6/6 + n5/2 + 5n4/12 - n2/12
S (n6) = n7/7 + n6/2 + n5/2 - n3/6 + n/42
S (n7) = n8/8 + n7/2 + 7n6/12 - 7n4/24 + n2/12
S (n8) = n9/9 + n8/2 + 2n7/3 - 7n5/15 + 2n3/9 – n/30
S (n9) = n10/10 + n9/2 + 3n8/4 - 7n6/10 + n4/2 - n2/12
S (n10) = n11/11 + n10/2 + 5n9/9 – n7 + n5 - n3/2 + 5n/66
Затем Я. Бернулли указал общую формулу
S(nc) = nc+1/c+1 + 1/2*nc + 1/2*( )Anc-1 + 1/4*( )Bnc-3 + 1/6*( )Cnc-5 +
+1/8*( )Dnc-7+ …
Здесь ( ), ( ) … - числа сочетаний; показатели степени n убывают, последний член в правой части содержит n или n2.
Числа A, B, C, D … - коэффициенты при n в выражениях S(n2), S(n4), S(n6), …
Именно: А=1/6, В=-1/30, С=1/42, D=-1/30,
Бернулли формулирует общее правило для вычисления этих чисел: сумма коэффициентов в выражениях S(n), S(n2), S(n3), … равна единице. Например, 1/9+1/2+2/3-7/15+2/9+D=1. Отсюда D=-1/30.
Я. Бернулли подчеркивает удобство таблицы фигурных чисел и заявляет, что с ее помощью в течение «половины четверти часа» нашел сумму десятых степеней первой тысячи натуральных чисел. Она оказалась равной
91 409 924 241 424 243 424 241 924 242 500.
1.2 Схема Бернулли. Обобщение
Определение 1. Схемой Бернулли называется последовательность независимых в совокупности испытаний, в каждом из которых возможны лишь два исхода - "успех" и "неудача", при этом успех в одном испытании происходит с вероятностью а неудача - с вероятностью .
Под независимостью в совокупности испытаний понимается независимость в совокупности любых событий, относящихся к разным испытаниям. В испытаниях схемы Бернулли, когда с одним испытанием можно связать только два взаимоисключающих события, независимость в совокупности испытаний означает, что при любом независимы в совокупности события успех в первом испытанииуспех в -м испытании. Эти события принадлежат одному и тому же пространству элементарных исходов, полученному декартовым произведением бесконечного числа двухэлементных множеств :
Здесь буквами "у" и "н" обозначены успешный и неудачный результаты испытаний соответственно.
Обозначим через число успехов, случившихся в испытаниях схемы Бернулли. Эта величина может принимать целые значения от нуля до в зависимости от результата испытаний. Например, если все испытаний завершились неудачей, то величина равна нулю.
Теорема 1 (формула Бернулли). При любом имеет место равенство:
Доказательство. Событие означает, что в испытаниях схемы Бернулли произошло ровно успехов. Рассмотрим один из благоприятствующих событию элементарных исходов:
когда первые испытаний завершились успехом, остальные неудачей. Поскольку испытания независимы, вероятность такого элементарного исхода равна . Другие благоприятствующие событию элементарные исходы отличаются лишь расположением успехов на местах. Есть ровно способов расположить успехов на местах. Поэтому событие состоит из элементарных исходов, вероятность каждого из которых также равна .
Определение 2. Набор чисел называется биномиальным распределением вероятностей.
1.2.1 Номер первого успешного испытания
Рассмотрим схему Бернулли с вероятностью успеха в одном испытании. Введем величину со значениями равную номеру первого успешного испытания.
Теорема 2. Вероятность того, что первый успех произойдет в испытании с номером равна
.
Доказательство. Вероятность первым испытаниям завершиться неудачей, а последнему - успехом, равна
Определение 3. Набор чисел называется геометрическим распределением вероятностей.
Геометрическое распределение вероятностей обладает интересным свойством, которое можно назвать свойством "нестарения".
Теорема 3. Пусть для любого . Тогда для любых неотрицательных целых и имеет место равенство:
Если, например, считать величину временем безотказной работы (измеряемым целым числом часов) некоторого устройства, то данному равенству можно придать следующее звучание: вероятность работающему устройству проработать еще сколько-то часов не зависит от того момента, когда мы начали отсчет времени, или от того, сколько уже работает устройство. Общепринятое название этого свойства - свойство отсутствия последействия.
Доказательство. По определению условной вероятности,
(1)
Последнее равенство следует из того, что событие влечет событие поэтому пересечение этих событий есть . Найдем для целого вероятность :
Можно получить еще проще: событие означает в точности, что в схеме Бернулли первые испытаний завершились неудачами, т.е. его вероятность равна . Возвращаясь к (1), получим
Теорема 3 доказана.
1.2.2 Независимые испытания с несколькими исходами
Рассмотрим схему независимых испытаний уже не с двумя, а с большим количеством возможных результатов в каждом испытании.
Пример 1. Игральная кость подбрасывается 15 раз. Найти вероятность того, что выпадет ровно десять троек и три единицы.
Здесь каждое испытание имеет три, а не два исхода: выпадение тройки, выпадение единицы, выпадение любой другой грани. Поэтому воспользоваться формулой для числа успехов в схеме Бернулли не удаcтся.
Попробуем вывести подходящую формулу. Пусть в одном испытании возможны исходов: , и -й исход в одном испытании случается с вероятностью , где .
Обозначим через вероятность того, что в независимых испытаниях первый исход случится раз, второй исход - раз, и т.д., наконец, -й исход - раз.
Теорема 4 (Обобщенная формула Бернулли). Для любого и любых неотрицательных целых чисел сумма которых равна верна формула
Доказательство. Рассмотрим один элементарный исход, благоприятствующий выпадению единиц, двоек и т.д.:
Это результат экспериментов, когда все нужные исходы появились в некотором заранее заданном порядке. Вероятность такого результата равна произведению вероятностей . Остальные благоприятные исходы отличаются лишь расположением чисел на местах. Число таких исходов равно числу способов расположить на местах единиц, двоек, и т.д. Это число равно
Теперь мы можем вернуться к примеру 1 и выписать ответ: вероятность получить десять троек, три единицы и еще два других очка равна
так как вероятности выпадения тройки и единицы равны по , а вероятность третьего исхода (выпала любая другая грань) равна
1.2.3 Теорема Пуассона для схемы Бернулли
Предположим, нам нужна вероятность получить не менее семи успехов в тысяче испытаний схемы Бернулли с вероятностью успеха . Вероятность этого события равна любому из следующих выражений, вычислить которые довольно сложно:
Сформулируем теорему о приближенном вычислении вероятности иметь успехов в большом числе испытаний Бернулли с маленькой вероятностью успеха . Термин "большое число" должен означать . Если при этом остается неизменной, то вероятность получить любое заданное число успехов уменьшается до нуля. Необходимо чтобы вероятность успеха уменьшалась одновременно с ростом числа испытаний. Но от испытания к испытанию вероятность успеха меняться не может (см. определение схемы Бернулли). Поэтому нам придется рассмотреть так называемую "схему серий": если испытание одно, то вероятность успеха в нем равна если испытаний два, то вероятность успеха в каждом равна и т.д. Если испытаний то в каждом из них вероятность успеха равна . Вероятность успеха меняется не внутри одной серии испытаний, а от серии к серии, когда меняется общее число испытаний. Обозначим через число успехов в -й серии испытаний.
Теорема 5 (теорема Пуассона). Пусть и так, что Тогда для любого вероятность получить успехов в испытаниях схемы Бернулли с вероятностью успеха стремится к величине
Доказательство. Положим . По условию . Подставим в формулу Бернулли:
(2)
В соотношении (2) мы воспользовались тем, что и замечательным пределом . Докажем последнее свойство:
Определение 4. Набор чисел называется распределением Пуассона с параметром .
По теореме 17 можно приближенно посчитать вероятность получить не менее семи успехов в тысяче испытаний схемы Бернулли с вероятностью успеха с вычисления которой мы начали. Поскольку "велико", а "мало", то, взяв можно записать приближенное равенство
(3)
Осталось решить, а достаточно ли велико, а мало, чтобы заменить точную вероятность на ее приближенное значение. Для этого нужно уметь оценивать разницу между этими вероятностями.
Следующую очень полезную теорему мы, исключительно из экономии времени, доказывать не станем.
Теорема 6 (уточненная теорема Пуассона). Пусть - произвольное множество целых неотрицательных чисел, - число успехов в испытаниях схемы Бернулли с вероятностью успеха . Cправедливо неравенство
Таким образом, теорема 6 предоставляет нам возможность самим решать, достаточно ли велико, а мало, руководствуясь полученной величиной погрешности. Какова же погрешность в формуле (3)? Взяв имеем
Таким образом, можно утверждать, что искомая вероятность заключена в границах .
Пример 2. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Решение. Событие А – достали белый шар. Тогда вероятности, . По формуле Бернулли требуемая вероятность равна
.
Пример 3. Определить вероятность того, что в семье, имеющей 5 деталей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
Решение. Вероятность рождения девочки , тогда .
Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:
, ,
, .
Следовательно, искомая вероятность
.
Пример 4. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.
Решение. Здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А - «появление нестандартной детали», его вероятность , тогда . Отсюда по формуле Бернулли находим.
Пример 5. При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.
Решение. Вычисляем по формуле Бернулли:
Пример 6. Независимые испытания продолжаются до тех пор, пока событие А не произойдет k раз. Найти вероятность того, что потребуется n испытаний (n < k), если в каждом из них .
Решение. Событие В – ровно n испытаний до k-го появления события А – есть произведение двух следующий событий:
D – в n-ом испытании А произошло;
С – в первых (n–1)-ом испытаниях А появилось (к-1) раз.
Теорема умножения и формула Бернулли дают требуемую вероятность:
цепь марков бернулли информатика
Глава 2. Цепи Маркова
2.1 Биография Маркова
Марков Андрей Андреевич. 2 (14) июня 1856—20 июля 1922 — русский математик, специалист по теории чисел, теории вероятностей и математическому анализу.
С 1886 — адъюнкт, с 1890 — экстраординарный, а с 1896 — ординарный академик Императорской Санкт-Петербургской Академии Наук.
Андрей Марков родился в семье мелкого чиновника в Рязанской губернии. В 1878 окончил Петербургский университет со степенью кандидата и в том же году получил золотую медаль за работу "Об интегрировании дифференциальных уравнений при помощи непрерывных дробей". С 1880 — приват-доцент, с 1886 — профессор, а с 1905 — заслуженный профессор Петербургского университета.
Научные исследования Марков тесно примыкают по своей тематике к работам старших представителей Петербургской математической школы — П.Л. Чебышева, Е.И. Золотарева и А.Н. Коркина. Блестящих результатов в области теории чисел Марков достиг в магистерской диссертации "О бинарных квадратичных формах положительного определителя" (1880). Результаты, полученные им в этой работе, послужили основой дальнейших исследований в этой области в СССР и за рубежом. В 1905 вышел в отставку. В этом же году ему присвоено звание заслуженного профессора Петербургского университета. Написал около 70 работ по теории чисел, теории приближения функций, теории дифференциальных уравнений, теории вероятностей, в т. ч. и 2 классических произведения — "Исчисление конечных разностей" и "Исчисление вероятностей". Труды Маркова по теории чисел касаются главным образом теории неопределенных квадратичных форм. Почти все они посвящены нахождению экстремальных квадратичных форм данного определителя.
Марков внес важный вклад в своеобразную область геометрии чисел, которая в настоящее время интенсивно развивается. Обогатил важными открытиями и методами также теорию вероятностей: развил метод моментов П.Л. Чебышева настолько, что стало возможным доказательство центральной предельной теоремы, существенно расширил сферу применения закона больших чисел и центральной предельной теоремы, распространив их не только на независимые, но и на зависимые опыты.
В цикле работ, опубликованных в 1906-1912, заложил основы одной из общих схем естественных процессов, которые можно изучать методами математического анализа. Впоследствии эта схема была названа цепями Маркова и привела к развитию нового раздела теории вероятностей — теории случайных процессов, которые играют важную роль в современной науке. В качестве примера случайных процессов можно назвать диффузию газов, химические реакции, лавинные процессы и т. д. Важное место в творчестве Маркова занимают вопросы математической статистики. Он вывел принцип, эквивалентный понятиям несмещенных и эффективных статистик, которые получили теперь широкое применение.
В математическом анализе Марков развил теорию моментов и теорию приближения функций, а также аналитическую теорию непрерывных дробей. Ученый широко использовал непрерывные дроби для приближенных вычислений в теории конечных разностей, интерполировании и т. д. Актуальность всех этих вопросов особенно возросла в связи с развитием вычислительной техники. Марков пользовался большим авторитетом среди студентов.
Он был материалистом и убежденным атеистом, бескомпромиссным борцом против религии. 12.02.1912 Марков подал в Синод прошение об отлучении его от церкви. Марков протестовал против решения царского правительства, отказывавшегося утвердить избрание А.М. Горького почетным членом Петербургской Академии Наук. АН СССР учредила премию им. А.А. Маркова за лучшие работы по математике. Именем Маркова назван кратер краевой зоны Луны.
Свой последний мемуар он представил Академии наук всего лишь за несколько месяцев до смерти. Тяжелый недуг свалил его в постель, и 20 июля 1922 г. он умер.
2.2 Цепи Маркова
Определение 5. Процесс, протекающий в физической системе, называется марковским, если в любой момент времени вероятность любого состояния системы в будущем зависит только от состояния системы в текущий момент и не зависит от того, каким образом система пришла в это состояние.
Определение 6. Цепью Маркова называется последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий Ai из полной группы. При этом условная вероятность pij(s) того, что в s –ом испытании наступит событие Aj при условии, что в (s – 1) – ом испытании наступило событие Ai, не зависит от результатов предшествующих испытаний.
Независимые испытания являются частным случаем цепи Маркова. События называются состояниями системы, а испытания – изменениями состояний системы. По характеру изменений состояний цепи Маркова можно разделить на две группы.
Определение 7. Цепью Маркова с дискретным временем называется цепь, изменение состояний которой происходит в определенные фиксированные моменты времени. Цепью Маркова с непрерывным временем называется цепь, изменение состояний которой возможно в любые случайные моменты времени.
Определение 8. Однородной называется цепь Маркова, если условная вероятность pij перехода системы из состояния i в состояние j не зависит от номера испытания. Вероятность pij называется переходной вероятностью.
Допустим, число состояний конечно и равно k. Тогда матрица, составленная из условных вероятностей перехода будет иметь вид:
Эта матрица называется матрицей перехода системы. Т.к. в каждой строке содержаться вероятности событий, которые образуют полную группу, то, очевидно, что сумма элементов каждой строки матрицы равна единице. На основе матрицы перехода системы можно построить так называемый граф состояний системы, его еще называют размеченный граф состояний. Это удобно для наглядного представления цепи. Порядок построения граф рассмотрим на примере.
Пример 7. По заданной матрице перехода построить граф состояний
Т. к. матрица четвертого порядка, то, соответственно, система имеет 4 возможных состояния. S1 0,2 0,7 S2 0,4 S4 0,6 0,5 0,1 0,5 S3.
На графе не отмечаются вероятности перехода системы из одного состояния в то же самое. При рассмотрении конкретных систем удобно сначала построить граф состояний, затем определить вероятность переходов системы из одного состояния в то же самое (исходя из требования равенства единице суммы элементов строк матрицы), а потом составить матрицу переходов системы. Пусть Pij(n) – вероятность того, что в результате n испытаний система перейдет из состояния i в состояние j, r – некоторое промежуточное состояние между состояниями i и j. Вероятности перехода из одного состояния в другое pij(1) = pij. Тогда вероятность Pij(n) может быть найдена по формуле, называемой равенством Маркова:
Здесь т – число шагов (испытаний), за которое система перешла из состояния i в состояние r. В принципе, равенство Маркова есть ни что иное как несколько видоизменная формула полной вероятности. Зная переходные вероятности (т.е. зная матрицу перехода Р1), можно найти вероятности перехода из состояния в состояние за два шага Pij(2), т.е. матрицу Р2, зная ее – найти матрицу Р3, и т.д. Непосредственное применений полученной выше формулы не очень удобно, поэтому, можно воспользоваться приемами матричного исчисления (ведь эта формула по сути – не что иное как формула перемножения двух матриц). Тогда в общем виде можно записать:
Вообще-то этот факт обычно формулируется в виде теоремы, однако, ее доказательство достаточно простое, поэтому приводить его не буду.
Орграфы возникают во многих жизненных ситуациях. Не пытаясь охватить большое число таких ситуаций, ограничимся рассмотрением одной из них.
Задача, которую мы рассмотрим, интересна сама по себе, а отчасти рассматриваем мы ее из-за того, что ее изложение не требует введения большого количества новых терминов.
Рассмотрим задачу об осле, стоящем точно между двумя копнами: соломы ржи и соломы пшеницы (рис. 1).
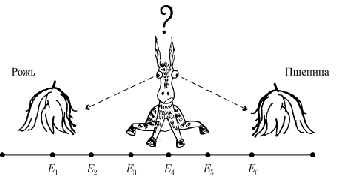
Осел стоит между двумя копнами: "Рожь" и "Пшеница" (рис. 1). Каждую минуту он либо передвигается на десять метров в сторону первой копны (с вероятностью ), либо в сторону второй копны (с вероятностью ), либо остается там, где стоял (с вероятностью ); такое поведение называется одномерным случайным блужданием. Будем предполагать, что обе копны являются "поглощающими" в том смысле, что если осел подойдет к одной из копен, то он там и останется. Зная расстояние между двумя копнами и начальное положение осла, можно поставить несколько вопросов, например: у какой копны он очутится с большей вероятностью и какое наиболее вероятное время ему понадобится, чтобы попасть туда?
Рис. 1
Чтобы исследовать эту задачу подробнее, предположим, что расстояние между копнами равно пятидесяти метрам и что наш осел находится в двадцати метрах от копны "Пшеницы". Если места, где можно остановиться, обозначить через ( — сами копны), то его начальное положение можно задать вектором , -я компонента которого равна вероятности того, что он первоначально находится в . Далее, по прошествии одной минуты вероятности его местоположения описываются вектором , а через две минуты — вектором . Ясно, что непосредственное вычисление вероятности его нахождения в заданном месте по прошествии минут становится затруднительным. Оказалось, что удобнее всего ввести для этого матрицу перехода.
Рис. 2
Пусть — вероятность того, что он переместится из в за одну минуту. Например, и . Эти вероятности называются вероятностями перехода, а -матрицу называют матрицей перехода (рис. 2). Заметим, что каждый элемент матрицы неотрицателен и что сумма элементов любой из строк равна единице. Из всего этого следует, что — начальный вектор-строка, определенный выше, местоположение осла по прошествии одной минуты описывается вектором-строкой , а после минут — вектором . Другими словами, -я компонента вектора определяет вероятность того, что по истечении минут осел оказался в .
Можно обобщить эти понятия. Назовем вектором вероятностей вектор-строку, все компоненты которого неотрицательны и дают в сумме единицу. Тогда матрица перехода определяется как квадратная матрица, в которой каждая строка является вектором вероятностей. Теперь можно определить цепь Маркова (или просто цепь) как пару , где есть -матрица перехода, а есть -вектор-строка. Если каждый элемент из рассматривать как вероятность перехода из позиции в позицию , а — как начальный вектор вероятностей, то придем к классическому понятию дискретной стационарной цепи Маркова. Позиция обычно называется состоянием цепи. Опишем различные способы их классификации.
Нас будет интересовать следующее: можно ли попасть из одного данного состояния в другое, и если да, то за какое наименьшее время. Например, в задаче об осле из в можно попасть за три минуты и вообще нельзя попасть из в . Следовательно, в основном мы будем интересоваться не самими вероятностями , а тем, положительны они или нет. Тогда появляется надежда, что все эти данные удастся представить в виде орграфа, вершины которого соответствуют состояниям, а дуги указывают на то, можно ли перейти из одного состояния в другое за одну минуту. Более точно, если каждое состояние представлено соответствующей ему вершиной , то, проводя из в для тех и только тех вершин, для которых , мы и получим требуемый орграф. Кроме того, этот орграф можно определить при помощи его матрицы смежности, если заменить каждый ненулевой элемент матрицы на единицу. Мы будем называть этот орграф ассоциированным орграфом данной цепи Маркова. Ассоциированный орграф одномерного случайного блуждания, связанного с задачей об осле, изображен на (рис. 3).
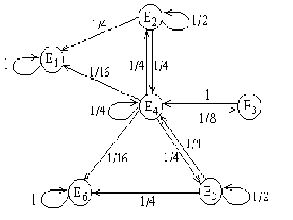
Другой пример: если цепь Маркова имеет матрицу перехода, приведенную на рис. 4, то ассоциированный орграф этой цепи выглядит так, как показано на (рис. 5).
Рис. 3
Рис. 4
Рис. 5
Теперь ясно, что в цепи Маркова из состояния в состояние можно попасть в том и только в том случае, если в ассоциированном орграфе существует орцепь из в , и что наименьшее возможное время попадания равно длине кратчайшей из таких орцепей. Цепь Маркова, в которой из любого состояния можно попасть в любое другое, называется неприводимой. Ясно, что цепь Маркова неприводима тогда и только тогда, если ее ассоциированный орграф сильно связан. Заметим, что ни одна из описанных выше цепей не является неприводимой.
При дальнейших исследованиях принято различать те состояния, в которые мы продолжаем возвращаться независимо от продолжительности процесса, и те, в которые мы попадаем несколько раз и никогда не возвращаемся. Более точно это выглядит так: если начальное состояние есть и вероятность возвращения в на некотором более позднем шаге равна единице, то называется возвратным (или рекурсивным) состоянием. В противном случае состояние называется невозвратным. В задаче об осле, например, очевидно, что состояния и являются возвратными, тогда как все другие состояния — невозвратными. В более сложных примерах вычисление нужных вероятностей становится очень хитрым делом, и поэтому проще бывает классифицировать состояния, анализируя ассоциированный орграф цепи. Нетрудно понять, что состояние возвратно тогда и только тогда, если существование простой орцепи из в в ассоциированном орграфе влечет за собой существование простой орцепи из в . В орграфе, изображенном на (рис. 3), существует простая орцепь из в , но нет ни одной орцепи из в . Следовательно, состояния и, аналогично, невозвратны ( возвратны). Состояние (такое, как ), из которого нельзя попасть ни в какое другое, называется поглощающим состоянием.
Другой прием классификации состояний опирается на понятие периодичности состояний. Состояние цепи Маркова называется периодическим с периодом , если в можно вернуться только по истечении времени, кратного . Если такого не существует, то состояние называется непериодическим. Очевидно, что каждое состояние , для которого , непериодическое. Следовательно, каждое поглощающее состояние — непериодическое. В задаче об осле не только поглощающее состояние , но и все остальные являются непериодическими. С другой стороны, во втором примере (рис. 5) поглощающее состояние — единственное непериодическое состояние, поскольку имеют период два, а — период три. Используя терминологию орграфов, легко показать, что состояние является периодическим с периодом тогда и только тогда, если в ассоциированном орграфе длина каждой замкнутой орцепи, проходящей через , кратна .
И, наконец, для полноты изложения введем еще одно понятие: назовем состояние цепи Маркова эргодическим, если оно одновременно возвратно и непериодично. Если любое состояние цепи Маркова является эргодическим, то назовем ее эргодической цепью.
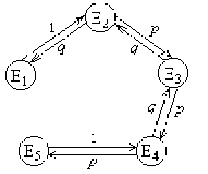
Пример 8. Частица, находящаяся на прямой, движется по этой прямой под влиянием случайных толчков, происходящих в моменты t1, t2, t3, ...Частица может находиться в точках с целочисленными координатами 1, 2, 3, 4, 5; в точках 1 и 5 находятся отражающие стенки. Каждый толчок перемещает частицу вправо с вероятностью и влево с вероятностью q, если частицы не находятся у стенки. Если же частица находится у стенки, то любой толчок переводит ее на единицу внутрь промежутка [1,5]. Найти матрицу перехода P и ей соответствующий граф.
Решение. Пусть Ei=(t) ,i = 1, 2, 3, 4, 5. Тогда граф перехода выглядит следующим образом:
Рис. 6
а матрица перехода –
Пример 9. Вероятности перехода за один шаг в цепях Маркова задаются матрицей:
Требуется:
а) найти число состояний;
б) установить, сколько среди них существенных и несущественных;
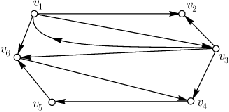
в) построить граф, соответствующий матрице P.
Решение.
а) 4 состояния.
б) состояния E1, E2 несущественны, поскольку остальные состояния достижимы из них, но E1 недостижимо из E4, а E2 недостижимо из E3; состояния E3 и E4 являются существенными.
Рис. 7. в)
Пример 10 (задача о скрещивании). В близко родственном скрещивании две особи, и среди их прямых потомков случайным образом выбираются две особи разного пола. Они вновь скрещиваются, и процесс этот продолжается бесконечно. Каждый родительский ген может передаваться с вероятностью 1/2, и последовательные испытания независимые. Имея три генотипа AA, Aа, аа для каждого родителя, мы можем различать шесть комбинаций родителей, которые пометим следующим образом:
У1=ФФ*ФФб У2= ФФ*Фаб У3 = ФФ*ааб У4 = Фа*Фаб У5= Фа*ааб У6=
аа*ааю
Найдите граф и матрицу перехода.
Решение.
Рассмотрим, какое потомство и с какой вероятностью может быть у особей разного пола, если они выбираются из E2.
Пусть Bi= {i-й потомок}, i= 1, 2 и B1,B2 - разного пола, тогда варианты потомков и их вероятности можно найти по следующему графу:
Рис. 8
Получаем, что
Аналогично, находим и вероятности других переходов:
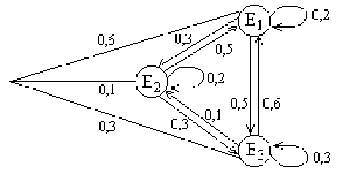
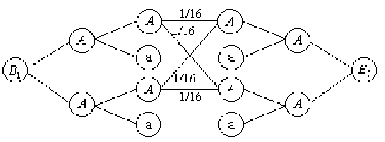
Тогда искомый граф перехода выглядит следующим образом:
Рис. 9
а матрица перехода –
Пример 11. Матрица вероятностей перехода цепи Маркова имеет вид:
Распределение по состояниям в момент времени t= 0 определяется вектором . Найти распределения по состояниям в момент t= 2.
Решение. Построим граф, соответствующий вектору начальных вероятностей и матрице перехода:
Рис. 10
По этому графу находим распределение по состояниям в момент t= 2:
P(E1)= (0,6*(0,2)2+ 0,6*0,3*0,5+0,6*0,5*0,6)+(0,1*0,5*0,2+0,1*0,2*0,5
+0,1*0,3*0,6) +(0,3*0,6*0,2+(0,3)2*0,6)+(0,3*0,1*0,5)=0,437;
P(E2)= (0,1*(0,2)2+0,1*0,5*0,3+0,1*0,3*0,1)+0,6*0,3*0,2+0,6*0,2*0,3
+0,6*0,5*0,1)+(0,3*0,1* 0,2+(0,3)2*0,1+0,3*0,6*0,3)=0,193;
P(E3)= 0,37.
Пример 12. Доказать, что P(n)= Pn для двух состояний цепи Маркова.
Решение. Пусть цепь Маркова с двумя состояниями E1 и E2 задана своей матрицей перехода P:
Докажем утверждение методом математической индукции.
Пусть n= 2. Тогда
Вероятности перехода за два шага удобно находить по графу перехода:
Рис. 11
Следовательно, P(2) = P2, и первый шаг метода математической индукции выполняется. Предположим далее, что при проверяемое утверждение истинно, т.е. P(k) = Pk, тогда матрица перехода за k+1 шаг P(k+1) = P(k) *P = Pk *P = P, что и требовалось доказать.
Глава 3. Применение цепей Маркова
3.1 Определение авторства текста
В статье посредством формального анализа текста решается задача определения авторства текста. Новый метод основывается на формальной математической модели последовательности букв текста как реализации цепи А.А. Маркова. Оказывается, частоты употребления пар букв очень хорошо характеризуют автора. Последнее утверждение проверено в объемном статистическом эксперименте на произведениях 82 писателей.
Введение опыта
В последние десятилетия наметилась тенденция поиска и выявления характерных структур авторского языка путем применения формально-количественных, статистических методов. Первые пробные шаги на этом пути предпринял еще в начале XIX века Н.А. Морозов. Интересно, что тогда же известный математик А.А. Марков выступил с критикой Н.А. Морозова. А.А. Марков критиковал Н.А. Морозова за то, что он не произвел тщательной статистической проверки утверждений относительно устойчивости некоторых элементов авторского стиля (например, частицы "не"). Примером правильного статистического подхода А.А. Марков считал свое исследование в статье, где он изучал распределение доли гласных и согласных среди первых 20000 букв "Евгения Онегина". Отметим, что работа посвящена первому применению "испытаний, связанных в цепь", получивших впоследствии название цепей А.А. Маркова. Работа удивительным образом предоставляет историческую основу методу определения авторства, изложенному в настоящей статье.
Истории вопроса определения авторства текста посвящена первая глава книги. Несмотря на то, что среди перечисленных в присутствуют весьма изощренные методики определения структуры авторского стиля, все они страдают, на взгляд автора настоящей статьи, одним общим недостатком. Ни одна из этих методик не проходила проверку на большом числе писателей. Дело в том, что многие из методик имеют трудно формализуемый этап сведения естественно-литературного произведения к предлагаемой математической модели. Например, для некоторых из них необходима классификация всех слов текста по грамматическим классам, что требует участия человека. При таком подходе большой вычислительный эксперимент с целью проверки методики на большом числе авторов практически неосуществим. Поэтому все такие методики пытались использовать на небольшом числе авторов.
Другого подхода придерживались авторы статьи. Они исследовали несколько простых параметров авторского стиля и на огромном числе произведений писателей XVIII-XX веков статистически доказали, что доля всех служебных слов в длинном прозаическом произведении является т.н. авторским инвариантом.
В настоящей статье предложен новый, независимый от, а также всех методик, перечисленных в, формальный метод установления автора текста. Наша постановка задачи отличается от. Мы предполагаем, что в нашем распоряжении имеются достаточно длинные фрагменты прозаических произведений ряда авторов на русском языке. Про некоторый анонимный фрагмент текста известно, что он принадлежит одному из этих авторов, но какому - неизвестно. Требуется узнать - кому именно.
Новый метод основывается на формальной математической модели последовательности букв текста как реализации цепи А.А. Маркова. По тем произведениям автора, которые достоверно им созданы, вычисляется матрица переходных частот употреблений пар букв. Она служит оценкой матрицы вероятностей перехода из буквы в букву. Матрица переходных частот строится для каждого из авторов. Для каждого автора оценивается вероятность того, что именно он написал анонимный фрагмент текста. Автором анонимного текста полагается тот, у которого вычисленная оценка вероятности больше.
Такой метод оказывается удивительно точным для естественно-языковых текстов. Мы обсуждаем здесь особенности применения метода и сравниваем его с методом определения автора на основе частот употребления каждой из букв в отдельности. Проверка метода проводилась на произведениях 82 писателей, среди которых есть русские писатели как XIX, так и XX века.
Математические основания
Марковская модель
Обозначим через A некоторое множество букв. Через Ak обозначим множество слов длины k над алфавитом A. Пусть A* = k > 0Ak. Обозначим длину слова f A* через f.
Задачу определения автора текста можно сформулировать следующим образом. Пусть заданы n классов Ci, где i = 0, ..., n1. В каждом классе Ci находятся последовательности fi,j A*, где j = 1, ..., mi, т.е. Ci = { fi,j j = 1,,mi}. Наша задача состоит в том, чтобы отнести x A* к одному из классов Ci.
Предположим, что последовательности букв fi,j являются реализациями цепи Маркова с переходной матрицей i. Построим оценку Pi. Обозначим через hi,j,kl число переходов букв k l в фрагменте fi,j, положим hi,kl = jhi,j,kl, а hi,k = lhi,kl. Положим Pikl = hi,kl/hi,k. Возможно, некоторые Pikl равны нулю. Обозначим через Zi множество таких упорядоченных пар (k,l), что Pikl > 0.
Предположим, что x также является реализацией цепи Маркова с матрицей переходных вероятностей P , где неизвестный параметр, который принимает одно из значений 1, ..., n.
Обозначим через k,l число переходов k l в x. Пусть также k = l k,l. Обозначим через
Li(x) = (k,l) k,l×ln(k,l /(Pikl×k)),
где сумма берется по парам (k,l) Zi. Грубо говоря, Li(x) равно минус логарифму вероятности x при условии, что x - реализация цепи Маркова с матрицей переходных вероятностей Pi. Назовем t(x) оценкой максимального правдоподобия для неизвестного параметра
t(x) = argmini = 0,...,n1 Li(x). (2.1)
Мы не будем обсуждать и доказывать какие-либо математические свойства оценки (2.1), хотя это и представляет интересную задачу математической статистики (более подробно см.). Зато мы покажем удивительную эффективность оценки (2.1) при установлении автора текста.
Схема эксперимента
Возьмем A = {маленькие буквы кириллицы}{символ пробела}. Предположим, что у нас имеются в распоряжении достаточно длинные фрагменты произведений n авторов на русском языке. Обозначим j-тый фрагмент i-того автора через gi,j. Можно считать, что фрагмент gi,j является последовательностью символов некоторого расширенного алфавита B, который включает, например, знаки пунктуации, большие буквы, латинские буквы и т.д. (на персональном компьютере B обычно совпадает с расширенным множеством символов ASCII).
Каждый фрагмент gi,j B* можно отобразить в A* посредством некоторой функции F: B* A*. Пусть, например, F превращает все заглавные буквы в маленькие, склеивает перенесенные слова, выбрасывает все знаки пунктуации и излишние знаки пробела, оставляя их по одному между словами, а также вставляет один пробел в начале и один пробел в конце фрагмента в случае отсутствия таковых.
Кроме того, мы будем рассматривать функцию G, которая устроена так же, как и функция F, с тем дополнением, что все слова, которые в фрагменте gi,j начинались с заглавной буквы, отбрасываются. Например, если
y = "Кроме того, мы будем рассматривать функцию G,", то
F(y) = " кроме того мы будем рассматривать функцию ", а
G(y) = " того мы будем рассматривать функцию ".
Теперь предположим, что некий фрагмент текста y B* принадлежит одному из n авторов, и нам неизвестно, кому именно. Наша задача: определить автора фрагмента y. Мы можем найти автора, применяя оценку (2.1) к последовательности x = F(y) или к x = G(y). Следовательно, мы получаем два способа определения автора:
1) истинный автор - t(F(y)),
2) истинный автор - t(G(y)).
Важно отметить, что оценки t(F(y)) и t(G(y)) вычисляются на основе информации о частотах употребления пар букв. Поскольку между словами вставлены пробелы, оценки t(F(y)) и t(G(y)) никак не зависят от порядка самих слов. По-видимому, t(F(y)) и t(G(y)) характеризуют последовательности морфем в словоформах русского языка, но, конечно, совсем не учитывают синтаксисическую информацию (на основе последней пытались устанавливать авторство в).
Обычно ни для одного из естественно-языковых текстов гипотеза о том, что он является реализацией соответствующей цепи А.А. Маркова, не выдерживает статистической проверки. Между тем, мы можем формально произвести все вычисления и найти оценку (2.1). Статистический эксперимент показывает, что авторы определяются очень уверенно.
Анализ частот употреблений букв (схема Бернулли)
Схемой Бернулли в теории вероятностей называется последовательность независимых одинаково распределенных случайных величин. Формально мы можем предположить, что последовательности fi,j и x являются реализациями последовательности независимых одинаково распределенных случайных величин, принимающих значения в A, а x распределен как величины класса , где - неизвестный параметр. Тогда оценка (2.1) принимает вид
e(x) = argmini Gi(x), (2.2)
где
Gi(x) = k k ln((k×hi)/(hi,k×)),
где сумма вычисляется по таким k, что k > 0, а = kk, hi = k hi,k и. Грубо говоря, производя оценку (x) мы производим частотный анализ текста. Статистический эксперимент показывает, что оценка e(x) существенно хуже оценки t(x).
Модельный эксперимент
Сначала проведем проверку нашей методики на следующем примере. Рассмотрим следующие произведения К. Булычева, А. Волкова, Н.В. Гоголя и В. Набокова.
Мы хотим проверить эффективность оценки t(F(y)). Предлагается следующий способ: выбрать каждого автора i (i = 0,1,2,3) по одному контрольному произведению y i, оценить матрицы i по другим произведениям fi,j, а затем найти t(F(yi)). Если оценка работает хорошо, то для каждого автора i должно быть t(F(yi)) = i.
0) К. Булычев: Умение кидать мяч ( y0); Белое платье золушки (g0,1); Великий дух и беглецы (g0,2); Глубокоуважаемый микроб (g0,3); Закон для дракона (g0,4); Любимец [Спонсоры] (g0,5); Марсианское зелье (g0,6); Миниатюры (g0,7); "Можно попросить Нину?" (g0,8); На днях землетрясение в Лигоне (g0,9); Перевал (g0,10); Показания Оли Н. (g0,11); Поминальник XX века (g0,12); Раскопки курганов в долине Репеделкинок (g0,13); Тринадцать лет пути (g0,14); Смерть этажом ниже (g0,15);
1) А. Волков: Семь подземных королей ( y1); Волшебник изумрудного города (g1,1); Урфин Джюс и его деревянные солдаты (g1,2); Огненный бог Марранов (g1,3); Гениальный пень (g1,4); На войне, как на войне (g1,5); О чем молчали газеты... (g1,6); Преступление и наказание (g1,7); Эпилог (g1,8); Желтый Туман (g1,9); Тайна заброшенного замка (g1,10);
2) Н.В. Гоголь: Рассказы и повести (y2, названия повестей: "Повесть о том, как поссорился Иван Иванович с Иваном Никифоровичем", "Старосветские помещики", "Вий", "Записки сумасшедшего"); Ревизор (g2,1); Тарас Бульба (g2,2); Вечера на хуторе близ Диканьки (g2,3);
3) В. Набоков: Другие берега (y3); Король, дама, валет (g3,1); Лолита (g3,2); Машенька (g3,3); Рассказы (g3,4); Незавершенный роман (g3,5).
Например, у А. Волкова контрольным произведением является y1, т.е. "Семь подземных королей" Все остальные произведения используются для вычисления i. Результаты вычислений представляются следующей таблицей.
Таблица 1
N
Автор
c1
c2
c3
c4
0
К. Булычев
0
15
2345689
75161
1
А. Волков
0
8
1733165
233418
2
Н.В. Гоголь
0
3
723812
243767
3
В. Набоков
0
5
1658626
367179
Столбец c2 содержит общее число файлов, в которых хранятся произведения автора. Заметим, что число файлов может не совпадать с числом произведений по двум причинам: во-первых, несколько произведений одного автора могут находится в одном файле (здесь такое произошло с А. Волковым - три повести "Желтый Туман", "Тайна заброшенного замка" и "Огненный бог Марранов" были в одном файле); во-вторых, одно большое произведение может разбиваться на несколько частей (последнее необходимо учитывать при изучении таблицы 2).
В колонке c3 содержится суммарное число символов (букв и пробелов) в F(gi,j): c3 = j F(gi,j). В колонке c4 содержится число символов в F(yi), т.е. c4 = F( yi). Например, для К. Булычева общий объем текстов jF(g0,j) составляет 2'345'689. Общий объем F(y1), т.е. число символов A в повести "Умение кидать мяч", выбранной в качестве контрольного текста, равно 75'161.
В столбце c1 в строке j находится ранг числа Lj(F( yj)) среди чисел {Li(F( yj)) i = 0,1,2,3}. Под рангом мы подразумеваем номер Lj(F(yj)) среди чисел {Li(F( yj)) i = 0,1,2,3}, расположенных в порядке невозрастания. Например, если j = 1 и Li расположились в порядке L0 L3 L2 L1, то рангом L1 будет 3. А если j = 0 и Li расположились в том же порядке L0 L3 L2 L1, то рангом L0 будет 0. Ранг Lj(F(yj)), среди чисел {Li(F( yj) i = 0,1,2,3} совпадает с рангом Lj(F(yj))/F(yj), среди чисел {Li(F(yj))/F(yj) | i = 0,1,2,3}. Расположим в строках j = 0,1,2,3 следующей матрицы по 4 числа Li(F( yj))/F( yj), i = 0,1,2,3:
В каждой строке найдем ранги чисел Li:
-
Искомые числа столбца c1 стоят на диагонали. Вспоминая формулу (2.1), мы заключаем, что t(F( yj)) = j тогда и только тогда, когда ранг Lj(F(yj))/F( yj) среди чисел {Li(F( yj))/F( yj) i = 0,1,2,3} просто равен 0. Следовательно, если в какой-либо строке в столбце c1 таблицы 1 стоит 0, то авторство контрольного текста определено правильно. Из таблицы 1 мы видим, что у всех писателей авторство определено верно.
Прежде, чем обсудить этот результат, поясним, почему столбец c1 задан таким образом. Дело в том, что если авторство определено неверно (т.е., оказалось t(F(yj)) j), то нас может интересовать, насколько мы были близки к правильному ответу. Если ранг Lj(F(yj))/F( yj) среди чисел {Li(F( yj))/F( yj) i = 0,1,2,3} равен 1, то мы ошиблись всего на одного писателя. Такой случай существенно лучше случая ранга Lj(F( yj))/F( yj) равного 3, поскольку тут правильный писатель оказывается в списке претендентов на его собственное произведение последним, что свидетельствует о большей ошибке.
Кроме того, матрица R сама по себе допускает интересные интерпретации. Например, из первой строки мы видим, что контрольное произведение К. Булычева "Умение кидать мяч" после самого К. Булычева больше походит на В. Набокова, затем на Н. Гоголя, и в последнюю очередь на произведения А. Волкова. Из последующих двух строк можно сделать вывод, что контрольные произведения А. Волкова и Н. Гоголя также в первую очередь походят на произведения В. Набокова. Может быть, это вызвано тем, что сам Набоков исторически находится между Н. Гоголем и парой писателей: А. Волковым и К. Булычевым? Если эта гипотеза верна, то наша метод чувствителен к исторической эпохе, в которую создано произведение. Некоторое подтверждение тому мы находим в последней строке матрицы R: контрольное произведение В. Набокова похоже в первую очередь на пару А. Волкова и К. Булычева, и лишь затем - на Н. Гоголя. Если бы пара А. Волкова и К. Булычева разбивалась Н. Гоголем. то мы имели бы аргумент против нашей гипотезы. Впрочем, возможны другие интерпретации матрицы R, и автор нисколько не настаивает на выше приведенной.
Можно интересоваться зависимостью матрицы R от
а) числа и объема текстов обучающих выборок;
б) однородности по жанру;
в) однородности по тематике;
г) длины контрольного текста;
д) единицы анализа (на уровне букв, слов и предложений)
и многих других параметров. Ниже мы приводим информацию относительно пункта а). Вкратце вывод таков: методика работает удовлетворительно (то есть, на диагонали матрицы R в основном стоят 0) при объеме обучающей выборки свыше 100 тысяч символов ASCII, и объеме контрольного текста свыше 100 тысяч символов ASCII.
Вернемся к обсуждению таблицы 1. Поскольку в столбце c1 все числа равны 0, авторство всех контрольных произведений определено верно. Результат тем более неожиданный, что мы использовали столь примитивную информацию о тексте, как частоты употребления пар букв. На самом деле простейший компьютерный эксперимент (результаты которого здесь не приведены) показал, что при небольшом числе подозреваемых писателей (меньше шести) даже оценка (2.2), основанная всего лишь на подсчете частот употребления букв, дает очень хорошие результаты. В следующем разделе описан значительно более объемный статистический эксперимент. Из него становится ясно, что методика устойчиво работает на очень большом числе авторов.
Результаты более объемного вычислительного эксперимента
В электронной библиотеке "Самые любимые книжки" нашлось n = 82 различных автора, которые творили в XIX-XX веках. Количество произведений разных авторов колебалось от 1 до 30 (например, у Аркадия и Бориса Стругацких). У немногих авторов, у которых нашлось лишь одно произведение (например, у Бориса Стругацкого), оно было поделено на две части, одна из которых использовалась в качестве контрольного текста. При отборе произведений учитывался объем: выбирались авторы, суммарный объем произведений которых превышал 100000 символов ASCII. Общее число произведений (романов, повестей, рассказов и т.п.) превысило 1000. Они были представлены в 386 файлах. Общий объем данных составил 128×106 символов ASCII.
Для каждого автора мы составили список gi,j текстов, из которых были получены оценки i, и оставили один текст yi, подлежащий распознаванию и не используемый при оценке i. Следуя схеме, описанной в предыдущем разделе, мы провели эксперименты для проверки качества оценок t(F(·)), t(G(·)), e(F(·)), e(G(·)) на этих 82 писателях. Для экономии места мы приведем лишь таблицу, отображающую информацию об эффективности оценки t(G(·)). Эта таблица составлялась подобно таблице 1. Ради экономии места соответствующие таблицы L и R не приведены.
Таблица 2
Автор
c1
c2
c3
c4
0
К. Булычев
0
15
2007724
64741
1
О. Авраменко
0
6
1733113
223718
2
А. Больных
0
6
1294721
373611
3
А. Волков
0
8
1478932
202495
4
Г. Глазов
0
5
1398323
184593
5
М. и С. Дяченко
0
5
1754213
197039
6
А. Етоев
0
5
267096
80358
7
А. Кабаков
0
4
905502
222278
8
В. Каплан
0
6
515029
129608
9
С. Казменко
3
4
1846161
156768
10
В. Климов
0
3
250231
179903
11
И. Крашевский
0
2
1183722
481795
12
И. Кублицкая
0
1
282377
170469
13
Л. Кудрявцев
1
3
583239
179093
14
А. Курков
0
6
628041
218726
15
Ю. Латынина
10
2
2628781
283565
16
А. Лазаревич
46
3
310553
94629
17
А. Лазарчук
0
5
2395669
210151
18
С. Лем
0
7
1568013
343519
19
Н. Леонов
0
2
568854
279377
20
С. Логинов
14
13
1998543
159247
21
Е. Лукин
0
4
602216
125694
22
В. Черняк
0
2
920056
201636
23
А.П. Чехов
0
2
662801
343694
24
И. Хмелевская
0
4
1524905
203684
25
Л. и Е. Лукины
0
3
837198
122999
26
С. Лукьяненко
0
14
3682298
483503
27
Н. Маркина
0
1
266297
93647
28
М. Наумова
0
3
306514
337821
29
С. Павлов
0
2
751836
453448
30
Б. Райнов
0
4
1405994
420256
31
Н. Рерих
0
3
1011285
211047
32
Н. Романецкий
2
6
1305096
117147
33
А. Ромашов
0
1
88434
87744
34
В. Рыбаков
0
6
715406
121497
35
К. Серафимов
0
1
186424
75276
36
И. Сергиевская
0
1
109118
50786
37
С. Щеглов
10
2
253732
55188
38
А. Щеголев
0
2
848730
105577
39
В. Шинкарев
29
2
156667
80405
40
К. Ситников
0
7
419872
109116
41
С. Снегов
0
2
824423
408984
42
А. Степанов
0
5
1223980
93707
43
А. Столяров
11
1
350053
137135
44
Р. Светлов
0
2
454638
268472
45
А. Свиридов
63
3
660413
235439
46
Е. Тильман
0
2
705352
464685
47
Д. Трускиновская
0
8
2005238
118351
48
А. Тюрин
0
18
4109050
110237
49
В. Югов
0
5
829209
66657
50
А. Молчанов
0
1
398487
206541
51
Ф.М. Достоевский
1
3
613825
88582
52
Н.В. Гоголь
0
3
638339
215540
53
Д. Хармс
0
2
199449
114889
54
А. Житинский
0
2
2137325
543037
55
Е. Хаецкая
2
2
723167
204091
56
В. Хлумов
0
3
788562
183358
57
В. Кунин
0
3
1335918
296463
58
А. Мелихов
0
1
615548
458086
59
В. Набоков
0
5
1522633
342774
60
Ю. Никитин
0
2
1342176
702383
61
В. Сегаль
0
2
320218
75917
62
В. Ян
0
1
507502
600636
63
А. Толстой
0
1
129664
97842
64
И. Ефремов
0
1
536604
256521
65
Е. Федоров
0
1
1120665
221388
66
О. Гриневский
0
1
158762
96085
67
Н. Гумилев
0
1
70181
71042
68
Л.Н. Толстой
0
1
1225242
199903
69
В. Михайлов
0
1
254464
84135
70
Ю. Нестеренко
0
1
352988
71075
71
А.С. Пушкин
0
1
170380
57143
72
Л. Резник
0
1
115925
79628
73
М.Е. Салтыков-Щедрин
0
1
239289
101845
74
В. Шукшин
0
1
309524
66756
75
С. М. Соловьев
0
1
2345807
160002
76
А. Кац
0
1
841898
81830
77
Е. Козловский
1
1
849038
889560
78
С. Есенин
0
1
219208
44855
79
А. Стругацкий
0
1
151246
51930
80
А. и Б. Стругацкие
0
29
6571689
345582
81
Б. Стругацкий
0
1
298832
261206
Первый вывод из данных этой таблицы состоит в том, что количество правильных ответов (нулей в колонке c1) очень велико - 69. Истинный автор произведения оказывается на втором месте в списке претендентов всего в трех случаях (в колонке c1 стоит 1): Л. Кудрявцев, Ф.М. Достоевский и Е. Козловский. На третьем месте (c1 = 2) - в двух случаях: Н. Романецкий и Е. Хаецкая. На четвертом месте оказывается лишь один автор (c1 = 3) - С. Казменко. Для остальных 7 авторов ошибка очень велика (Ю. Латынина, А. Лазаревич, С. Логинов, С. Щеглов, В. Шинкарев, А. Столяров, А. Свиридов). Они не оказываются даже в десятке претендентов на их собственные произведения.
Мерой неточности оценки t(G(·)) может служить средний ранг, равный сумме чисел в колонке c1, деленной на общее число писателей 82. Здесь средний ранг равен
2.35 (3×1+2×2+1×3+2×10+1×11+1×14+1×29+1×46+1×63) / 82
Все эти числа приведены в таблице 3 в колонке t(G(·)). Если выбросить семерых плохо определяемых авторов, средний ранг окажется равным
0.13 2/15 = (3×1+2×2+1×3) / 75.
Второй вывод из данных таблицы 2 состоит в том, что метод работает и на стихотворных произведениях (А.С. Пушкина, С. Есенина и Н. Гумилева). В-третьих, правильно определяются писатели, чьи произведения переводились с польского языка (С. Лем и И. Хмелевская). В-четвертых, среди плохо распознаваемых авторов нет общепризнанных классиков русской литературы.
Для сравнения, в следующей таблице приведены результаты аналогичного исследования с оценками t(F(x)), e(F(x)), e(G(x)) на тех же текстах.
Таблица 3
c1
t(F(·))
t(G(·))
e(F(·))
e(G(·))
0
57
69
1
2
1
4
3
8
8
2
4
2
7
13
3
4
1
2
2
4
0
0
3
7
5
13
7
61
50
Среднее
3.50
2.35
13.95
12.37
Сделаем два вывода на основании данных последней таблицы. Во-первых, частотный анализ (метод, основанный на схеме Бернулли) работает плохо (имеется максимум два точных ответа). Однако, он все-таки дает какую-то информацию об авторе, ибо в случае совершенно случайного выбора истинного автора средний результат в последних двух столбцах был бы около 40. Во-вторых, выбрасывание слов, начинающихся с заглавной буквы, заметно улучшает результаты (даже при частотном анализе). Действительно, столбцы с функцией G(·) заметно лучше столбцов с функцией F(·).
Заключение проведенного опыта
Из данных таблицы 3 хорошо видно, что оценка (2.1), основанная на анализе числа употреблений диад (двухбуквенных сочетаний), значительно эффективней оценки (2.2), основанной на частотном анализе одиночных букв, и правильно указывает автора с большой долей уверенности (84% против 3%). Можно было бы ожидать превосходство оценки (2.1), поскольку она использует больше информации об исходном тексте. Следует подчеркнуть удивительную точность (2.1) при распознавании истинного автора произведения (например, метод авторского инварианта принципиально не может различить более 10 писателей, а здесь рассмотрено свыше 80). Такая точность несомненно должна привлечь внимание к изложенному методу.
Отмечается существенное улучшение качества распознавания автора текста при выбрасывании слов, начинающихся с заглавной буквы. Этот феномен еще требует своего объяснения.
Как уже говорилось, А.А. Марков весьма интересовался задачей определения авторства текста (об этом свидетельствует его статья). Знаменательно, что его собственная идея о "связи испытаний в цепь", опробованная им же на литературном материале, привносит прогресс в решение этой задачи.
3.2 Применение PageRank
На данный момент Google является одной из самых популярных поисковых систем Интернет. При поиске и ранжировании документов Google основывается на содержании страницы, ключевых словах в заголовке и описании. Но так же система опирается на значения PageRank. PageRank является числом, отображающим важность страницы. Таким образом, после того как учтено содержание страницы, ключевые слова на ее положение влияет значение PageRank.
Если рассматривать поведение абстрактного пользователя сети, который нажимает на ссылки случайным образом и при этом в любой момент может закрыть браузер и прекратить просмотр по каким-либо причинам, то здесь естественным образом возникает вопрос, с какой вероятностью случайный пользователь попадет на ту или иную страницу и от чего эта вероятность зависит. Очевидно, что если на страницу нет ни одной ссылки, то ни уйти с нее, ни попасть на нее практически невозможно. Также если все страницы сети ссылаются на какую-то одну, то вероятность просмотра такой страницы пользователем значительно повышается. При этом вероятность посещения страниц, на которые в свою очередь будет ссылаться эта, тоже повысится. Таким образом, вероятность просмотра страницы зависит от количества ссылок на нее и от вероятности просмотра страниц ссылающихся на нее. Видимо, именно для расчета вероятности посещения страницы был разработан алгоритм PageRank.
Реализация алгоритма расчета PageRank неизвестна наверняка, но общий принцип самого алгоритма был опубликован в статье «The Anatomy of a Large-Scale Hypertextual Web Search Engine».
Для расчета PageRank используется следующая формула:
PR(A) = (1-d) + d∙ ( PR(T1)/C(T1) + … + PR(TN)/C(TN)) (1),
где PR(A) – PageRank страницы А;
T1… Tn – страницы, ссылающиеся на А;
C(T1) – количество ссылок страницы T1;
d – коэффициент затухания, находится в пределах от 0 до 1, обычно равен 0,85.
Также на PageRank наложено ограничение:
∑PRj = N, j=1…N (2),
где N – количество страниц в сети.
Данное условие следует из того, что сумма всех вероятностей не может превышать единицу, т.е. вероятность пребывания на данной странице равна отношению значения PageRank к числу всех страниц.
Для учета вероятности того, что пользователь закроет страницу, введен коэффициент затухания d.
Расчет PageRank помогает учитывать индивидуальность каждой страницы сети. Также один из плюсов PageRank заключается в том, что в связи со сложностью алгоритма его расчета на него практически невозможно влиять искусственным образом.
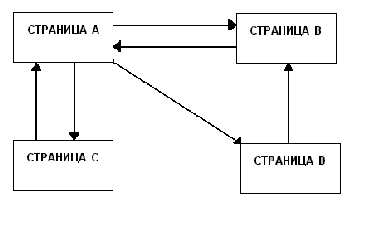
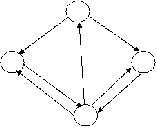
Рассмотрим расчет PageRank для простейшей сети, состоящей из четырех страниц (рис. 1).
Рис. 1.
Пусть изначально PageRank всех страниц равен 1.
Теперь посчитаем значения PageRank на первом шаге, используя (1):
PR(A) = (1-0,85) + 0,85∙ ( PR(B)/1 + PR(C)/1).
Затем подставим в формулу PR(B) и PR(C) равные 1:
PR(A) = 0,15 + 0,85∙ ( 1/1 + 1/1) = 1,85.
Для B:
PR(B) = (1-0,85) + 0,85∙ ( PR(A)/3 + PR(D)/1) = 0,15 + 0,85∙ ( 1/3 + 1/1) =
1,28333.
Для C:
PR(C) = (1-0,85) + 0,85∙ ( PR(A)/3) = 0,15 + 0,85∙ ( 1/3) = 0,43333.
Для D:
PR(D) = (1-0,85) + 0,85∙ ( PR(A)/3) = 0,15 + 0,85∙ ( 1/3) = 0,43333.
В результате мы получили новые значения PageRank для всех страниц.
Теперь посчитаем значения PageRank на втором этапе:
PR(A) = 0,15 + 0,85∙ ( PR(B)/1 + PR(C)/1)
Здесь мы опять подставим PR(B) и PR(C), но уже равные не 1, а их значения, полученные на предыдущем шаге:
PR(A) = 0,15 + 0,85∙ (1,28333/1 + 0,43333/1) = 1,609.
Для остальных страниц:
PR(B) = 0,15 + 0,85∙ ( PR(A)/3 + PR(D)/1) = 0,15 + 0,85∙ (1,85/3 +
0,43333/1) = 1,425.
PR(C) = 0,15 + 0,85∙ ( PR(A)/3) = 0,15 + 0,85∙ ( 1,85/3) = 0,674.
PR(D) = 0,15 + 0,85∙ ( PR(A)/3) = 0,15 + 0,85∙ ( 1,85/3) = 0,674.
Таким образом, мы получили значения PageRank на втором шаге, которые будут использоваться при расчете значений PageRank на третьем шаге. Затем необходимо проделывать эту операцию снова и снова, используя каждый раз значения PageRank рассчитанные на предыдущем этапе.
Смысл заключается в том, что нам придется проделать достаточно большое количество шагов (чем больше страниц в системе, тем больше будет количество шагов) и в результате после какого-то шага n на всех последующих шагах, начиная с n+1, значения PageRank будут неизменными. Для нашего примера достаточно проделать 10 шагов, чтобы значения PageRank выглядели следующим образом:
PR(A) = 1,637;
PR(B) = 1,136;
PR(C) = 0,614;
PR(D) = 0,614.
На 11 шаге, используя эти значения, мы получим новые PR, которые будут равны этим. На 12, 13, …,т.е. на всех последующих этапах произойдет тоже самое. Таким образом, можно сказать, что это и есть значения PageRank для данной системы. Сумма всех PR равна 4, т.е. условие (2) выполняется.
Также PageRank можно рассчитать не итерационным методом, как это сделано выше, а матричным.
Для этого составляется матрица следующего вида:
Данная матрица соответствует нашей простейшей сети (Рис.1.), т. е. страница A ссылается на B, C, D. Страница B ссылается на A. Страница C ссылается на А и D ссылается на В. При этом значения каждой строки делятся на количество ссылок данной страницы. Т.е. значения строки А поделены на 3, а значения всех остальных строк поделены на 1.
Данную матрицу необходимо умножить на значения PR предыдущего шага, полученный вектор умножить на единичный вектор, умноженный на d, и прибавить к результату единичный вектор, умноженный на (1-d).
После расчета мы видим, что страница A имеет самый высокий PR в нашей сети, страница B – более низкий, т.е. вероятность попасть на страницу A больше всего. Поэтому если все четыре страницы, будут по содержанию соответствовать какому-то запросу поиска, то несмотря на достаточно похожее содержание страниц, после учета значений PR, страница A окажется на первом месте, B – на втором, а C и D – на третьем.Поскольку PageRank, имеет отношение к вероятности просмотра страниц, то для лучшего понимания, стоит обратиться к такому разделу теории случайных процессов как теории Марковских процессов.
Под Марковским процессом подразумевается процесс, для которого вероятность находиться в данном состоянии, на данном этапе процесса можно вывести из информации о предшествующем состоянии. Цепью Маркова называется Марковский процесс, для которого каждое конкретное состояние зависит только от непосредственно предыдущего. Число состояний цепи Маркова конечно, а вероятности перехода из одного состояния в другое не зависят от времени.
Следуя из определения можно сказать, что рассматриваемый нами процесс поведения абстрактного пользователя сети является Марковским, и даже более того, является Цепью Маркова.
Теперь рассмотрим, какие условия определяют цепь Маркова:
Во-первых, у цепи имеется матрица вероятностей перехода:
где pij – вероятность перехода из состояния i в состояние j за один шаг процесса.
Матрица (3) обладает следующими свойствами:
а) ∑pij = 1 j=1…N. (свойство, вытекающее из замкнутости системы);
б) pij ³ 0 ” i,j.
Во-вторых, у цепи Маркова имеется вектор начальных вероятностей, который описывает начальное состояние системы:
P(0) = < P01, P02,..,P0n > (4)
Обозначим шаги (этапы) процесса за t = 0, 1,…..
Если P(0) это вектор начальных вероятностей, то P(t) – это вероятностный вектор на шаге t. Значение P(t+1) зависит от P(t). Формула расчета в матричном виде выглядит следующим образом:
P(t+1) = P(t) ∙P (5).
Отсюда следует, что:
P(t) = P(0) ∙Pt (6).
В теории цепей Маркова показано, что в пределе, при t стремящемся к бесконечности, вероятности состояний стремятся к определенным предельным значениям, которые удовлетворяют соотношению:
P(*)=P(*)∙P (7).
Из (7) становится очевидным, следующее важное свойство предельных векторов вероятностей P(*). Заключается оно в том, что P(*) является единственным и не зависит от вектора начальных вероятностей P(0) и определяются только матрицей вероятностей перехода.
Теперь рассмотрим применение данной теории для системы из нашего примера (Рис. 1. Часть I).
Матрица вероятностей перехода будет выглядеть следующим образом, т.е. также как и матрица при расчете PageRank матричным способом:
Первая строка матрицы свидетельствует о следующем: со страницы A можно перейти на B, C, и D. Вероятность того, что после A пользователь выберет C равна 1/3. Вероятность выбора D или C тоже равна 1/3.
Вторая строка значит, что со страницы B можно попасть только на A, вероятность этого перехода равна 1. Третья строка – с C можно попасть только на A, вероятность перехода равна 1. Четвертая строка – с D можно попасть только на B, вероятность перехода равна 1.
Для нашей системы вектор начальных вероятностей выглядит следующим образом (поскольку в нашей сети четыре страницы и пользователь может оказаться на любой из них с одинаковой вероятностью):
P(0) = < 1/4, 1/4, 1/4, 1/4>.
Для расчета вектора P(1) применим формулу (5), т.е. P(0) умножим на матрицу вероятностей перехода. Получим P(1) = <0,5; 0,3333; 0,0833; 0,0833>.
Для вектора P(2) формула (5) имеет следующий вид: P(2) = P(1) ∙P. После расчета получаем значения P(2) = <0,4167; 0,25; 0,167; 0,167>.
Рассчитывая значения P(t) по формуле (5) мы найдем t, для которого выполняется равенство (7). Т.е. мы рассчитаем значение предельного вектора вероятностей P(*), который не зависит от вектора начальных вероятностей P(0) и определяется только матрицей вероятностей перехода.
В нашем случае P(*) = <0,429; 0,286; 0,143; 0,143>.
Таким образом, после достаточно большого количества переходов со страницы на страницу уже не имеет значения с какой страницы пользователь начал просмотр, поскольку в результате он окажется на странице A с вероятностью 0,429, на странице B с вероятностью 0,286, на страницах C и D с вероятностями 0,143 (или можно сказать, что 42% пользователей будут на странице A, 29% будут на странице B и на страницах C и D будет по 14% посетителей). Теперь с полученным вектором P(*) произведем следующие действия: 0.85∙4P(*) + (1-0,85)
Проведем расчеты:
Для А: 0,85∙4∙0,429 + 0,15 = 1,607.
Для B: 0,85∙4∙0,286 + 0,15 = 1,12.
Для C: 0,85∙4∙0,143 + 0,15 = 0,635.
Для D: 0,85∙4∙0,143 + 0,15 = 0,635.
Получается что, рассчитав предельный вектор вероятностей P(*), умножив его на единичный вектор, умноженный на 4d, и прибавив к нему единичный вектор, умноженный на (1-d), мы получили значении практически равные значениям PR, рассчитанным в первой части статьи.
Сравним два алгоритма (расчет PageRank матричным способом и нахождение предельного вектора P(*) Цепи Маркова) в общем случае. Различие заключается лишь в том, что при расчете значений PR за начальный берется единичный вектор и вводится зависимость PR от коэффициента затухания. А для расчета P(*) начальный вектор состоит из значений 1/N, где N – количество страниц. Именно поэтому, умножив полученный вектор P(*) на N и d, а также прибавив (1-d) мы получили значения близкие к значениям PR.
Заключение
В заключение своей работы я хочу сказать, что я не пожалел, что выбрал эту тему. Тем более что есть некоторые варианты продвижения этой темы на языки программирования, что не менее интересно.
Я считаю, что рассмотрел материал работы подробно, и старался как можно более доступно изложить информацию по данной теме. Есть некоторые практические отступления, которые помогают понять всю сложность формул, или теорем. При решении этих задач, понимаешь. Что не все так сложно, как могло показаться на первый взгляд.
Я так думаю, что будущее нашей современной математики в области теории вероятности будет за Марковскими цепями. Чем лучше мы будем в них разбираться, тем проще мы сможем «владеть» современным миром.
Список литературы
1. Андрухаев Х.М. Курс по Теории вероятности
2. Гмурман «Теория вероятности и математической статистике» 1999г.
3. Гнеденко «Курс теории вероятности», 1954г.
4. Гунир П.С. Овчинский Б.В. «Основы Теории Вероятности»
5. Емельянов «Задачник по теории вероятности»
6. Прохоров, Розанов. Справочная математическая библиотека «Теория вероятности» 1967г.
7. Свешников А.А. «Сборник задач по теории вероятности, мат. Статистике и теории случайных функций»
8. Http://www.erudition.ru

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ