Синтез и анализ логической схемы при кубическом задании булевой функции
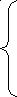

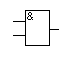



 Министерство образования Российской Федерации
Министерство образования Российской Федерации
Томский политехнический университет
Факультет автоматики и вычислительной техники
Кафедра вычислительной
техники
Курсовая работа
по дисциплине “Теория автоматов”
на тему: «Синтез и анализ логической схемы при кубическом задании булевой функции»
Томск 2009
СОДЕРЖАНИЕ
Введение
Нахождение минимального покрытия
Построение факторизованного покрытия
Составление логической схемы на основе данного базиса логических элементов
Нахождение по пи-алгоритму Рота единичного покрытия
Синтез контролирующего теста. Контроль схемы тестом
Заключение
Литература
ВВЕДЕНИЕ
Аппарат алгебры логики широко применяется в теории ЦВМ, в частности для решения задач анализа и синтеза схем. При решении задачи синтеза исходное логическое выражение, описывающее некоторую логическую функцию, преобразуется и упрощается так, чтобы каждый член полученного эквивалентного логического выражения мог быть представлен простой схемой. Таким образом, при синтезе вычислительных и управляющих схем составляется математическое описание задачи в виде формул алгебры логики. Затем производится минимизация исходной формулы и из числа эквивалентных логических схем выбирается та, которая допускает наиболее простую реализацию.
В данной курсовой работе стоит задача синтеза схемы, реализующей функцию, заданную кубическим комплексом к(f). В табл. 1 приведено исходное покрытие из 8 кубов. Логическую схему следует построить в универсальном базисе элементов ИЛИ-НЕ, который характеризуется коэффициентом объединения по входу к(вх)=4 и коэффициентом разветвления по выходу к(р)=2. Стоимость покрытия равна 48.
Таблица 1
Обозначение куба
Покрытие
Размерность куба
a
1011X10
6
b
1X1XX11
4
c
1011X11
6
d
XX1X1X0
3
e
0X11111
6
f
00X0XX0
4
g
0X00101
6
h
10X00X0
5
Порядок выполнения работы можно определить следующим образом:
1). Нахождение минимального покрытия;
2). Построение факторизованного покрытия;
3). Составление логической схемы на основе данного базиса логических элементов;
4). Нахождение по пи-алгоритму Рота единичного покрытия;
5). Построение контролирующего теста;
6). Проверка логической схемы контролирующим тестом.
1. НАХОЖДЕНИЕ МИНИМАЛЬНОГО ПОКРЫТИЯ
В первую очередь необходимо найти минимальное в смысле Кванта покрытие. Минимальное покрытие булевой функции ищется в два этапа:
1).получение минимального множества Z простых импликант;
2).выделение L-экстремалей на множестве Z.
Для выполнения этих этапов используются операции *-произведения, #-вычитания кубов.
При выполнении операции *-произведения одного куба на другой получается новый куб, противоположные грани которого лежат в исходных кубах. Этот новый куб может стать простой импликантой исходного покрытия. Надо иметь в виду, что куб является простой импликантой исходного покрытия, если он не составляет грань никакого другого комплекса К или того куба, который получился при произведении в процессе нахождения простых импликант. Это означает, что простые импликанты при *-произведении не дают новых кубов, не входящих в предыдущие кубы.
При нахождении простых импликант выполняются все попарные произведения с учетом того, что произведение куба самого на себя приводит к кубу, участвующему в произведении; что произведение первого куба на второй равно произведению второго куба на первый.
Операция *-произведения двух кубов а=а1а2…аi…an и b=b1b2…bi…bn определяется на основе табл. 2.
Таблица 2
ai * bi
ai
0
1
X
bi
0
0
Y
0
1
Y
1
1
X
0
1
X
Если значение Y получается только в одной координате, то произведение кубов a и b дает так называемый вновь образованный куб, в котором величина Y заменяется на X. Если же имеется более одной координаты Y, то звездчатое произведение дает 0.
Процесс нахождения множества простых импликант является циклическим. В каждом цикле вначале удаляются те кубы исходного покрытия, которые являются гранями других кубов этого покрытия. Далее удаляются кубы исходного покрытия, являющиеся гранями кубов покрытия. Должны быть удалены полученные при *-произведении кубы, являющиеся гранями кубов покрытия. И наконец, удаляются полученные кубы с размерностью, на единицу меньшей номера цикла. Оставшиеся в таблице кубы передаются на следующий цикл *-произведения. Циклы выполняются до тех пор, пока перестанут появляться вновь образованные кубы. Процесс нахождения множества простых импликант для 35-го варианта приведен в табл. 3,4,5,6. Куб «с» не используется при нахождении данного множества, т.к. он входит в куб «b».
1 цикл нахождения множества простых импликант Таблица 3
1011X10
1X1XX11
XX1X1X0
0X11111
00X0XX0
0X00101
1011X10
-
1X1XX11
1011X1X
-
XX1X1X0
1011110
1X1X11X
-
0X11111
XX11111
0X1111X
-
00X0XX0
00101X0
-
0X00101
000010X
-
10X00X0
101X010
101001X
1010XX0
X0X00X0
2 цикл нахождения множества простых импликант Таблица 4
1Х1ХX11
XX1X1X0
00X0XX0
0X00101
1011X1X
101X010
1X1X11X
XX11111
101001X
0X1111X
1010XX0
000010X
1X1XX11
-
XX1X1X0
-
00X0XX0
-
0X00101
-
1011X1X
1011X11
101111X
-
101X010
101X01X
101XX10
Y010010
1011010
-
1X1X11X
1X1X111
1X1X110
Y010110
101111X
101XY10
-
XX11111
1X11111
XX1111X
1011111
1X11111
-
101001X
1010011
1010Y10
Y010010
101X01X
1010010
1010Y1X
-
0X1111X
XX11111
0X11110
001Y110
X01111X
YX1111X
0X11111
-
1010XX0
1010X1X
10101X0
X010XX0
101XX10
1010010
1010110
1010010
-
000010X
00Y0100
0000100
0000101
-
X0X00X0
101001X
X010XX0
00X00X0
0000Y01
101Y010
1010010
1010Y10
1010010
10100X0
0000Y00
3 цикл нахождения множества простых импликант Таблица 5
1X1XX11
XX1X1X0
00X0XX0
0X00101
1011X1X
1X1X11X
000010X
X0X00X0
101X01X
1010X1X
101XX10
XX1111X
1X1XX11
-
XX1X1X0
-
00X0XX0
-
0X00101
-
1011X1X
-
1X1X11X
-
000010X
-
X0X00X0
-
101X01X
101X011
101XX10
X010010
101101X
101XX1X
1010010
-
1010X1X
1010X11
1010110
X010X10
101XX1X
101011X
1010010
101001X
-
101XX10
101XX1X
101X110
X010X10
1011X10
101X110
1010010
101X010
1010X10
-
XX1111X
1011111
XX11110
001X110
101111X
1X1111X
1011X1X
101X11X
1011110
-
X010XX0
1010X1X
X0101X0
0010XX0
101XX10
1010110
00X0100
X0100X0
1010010
1010X10
1010X10
X01X110
4 цикл нахождения множества простых импликант Таблица 6
1X1XX11
XX1X1X0
00X0XX0
0X00101
000010X
X0X00X0
XX1111X
X010XX0
101XX1X
1X1XX11
-
XX1X1X0
-
00X0XX0
-
0X00101
-
000010X
-
X0X00X0
-
XX1111X
-
X010XX0
-
101XX1X
101XX11
101X110
X010X10
1010010
101111X
1010X10
-
1X1X11X
1X1X111
1X1X110
X010110
1010X10
1X1111X
1010110
101X11X
В таблицах 3, 4, 5 и 6 опущены те *-произведения, которые были рассмотрены раньше. Множество простых импликант Z выглядит следующим образом:
Z={ 1X1XX11, XX1X1X0, 00X0XX0, 0X00101, 000010X, X0X00X0, XX1111X, X010XX0, 101XX1X,1X1X11X }.
Стоимость данного покрытия составляет 53, что на 5 больше стоимости исходного покрытия.
После нахождения множества Z в нем необходимо выделить такое подмножество, которое покрывало бы все вершины из комплекса L и имело бы минимальную стоимость по Квайну. В основе лежит понятие L-экстремали, то есть куба Zi, содержащего в себе одну или несколько вершин из комплекса L (L=C), которой нет ни в одной другой простой импликанте из множества Z.
Куб Zi является L-экстремалью, если для него выполняется следующее соотношение:
[ Zi # ( Z - Zi)] L ,
где # - знак операции вычитания кубов.
Операция вычитания, например, из куба а куба b служит для удаления их общей части, т.е. их пересечения, из куба а. Эта операция определяется следующим образом:
Координатное вычитание кубов ( ai # bi ) Таблица 7
ai # bi
ai
0
1
X
bi
0
Z
Y
1
1
Y
Z
0
X
Z
Z
Z
Операция вычитания из куба а куба b определяется следующим образом:
a, при наличии Y,
a # b = , если ai # bi = Z,
( a1a2…ai-1iai+1…an),
где i = 0 или 1, объединение берется по всем таким i.
Процесс выделения L-экстремали является циклическим, на каждом цикле очередная простая импликанта вычитается из предыдущей разности. Процессы вычитания и пересечения для полученных выше простых импликант отражены в табл. 8.
Выделение L-экстремалей Таблица 8
Z1
1X1XX11
Z2
XX1X1X0
Z3
00X0XX0
Z4
0X00101
Z5
000010X
Z6
X0X00X0
Z7
XX1111X
Z8
X010XX0
Z9
101XX1X
Z10
1X1X11X
1
2
3
4
5
6
7
8
9
10
11
12
Z1
1X1XX11
-
0ZZZZ0Y
XX1X1X0
YZ0ZZ0Y
00X0XX0
YZYZZYZ
0X00101
YZYZZY0
000010X
0Z0ZZ0Y
X0X00X0
0ZZZZZZ
0X1111X
0ZZZZ0Y
X010XX0
ZZZZZZ0
101XX10
ZZZZZZ0
1X1X110
Z2
XX1X1X0
ZZZZ0ZY
1X1XX11
-
ZZ0Z0ZZ
0000XX0
00X00X0
ZZYZZZY
0X00101
ZZYZZZ1
000010X
ZZ0ZYZZ
X0X00X0
ZZZZZZ1
0X11111
ZZZZ0ZZ
X0100X0
ZZZZ0ZZ
101X010
ZZZZZZZ
Z3
00X0XX0
Y1Z1ZZY
1X1XX11
11Z1ZZZ
1X1X1X0
X11X1X0
XX111X0
-
Z1ZZZZY
0X00101
ZZZZZZ1
0000101
1ZZZZZZ
10X00X0
Z1ZYZZY
0X11111
1ZZZZZZ
10100X0
YZZ1ZZZ
101X010
Z4
0X00101
YZY10YZ
1X1XX11
YZY1Z1Y
1X1X1X0
1ZY1Z1Y
X11X1X0
1ZYYZ1Y
XX111X0
ZZZZ01Y
0000XX0
ZZ1ZY1Y
00X00X0
-
ZZZZZZZ
YZ1ZY1Y
10X00X0
ZZYYZYZ
0X11111
YZYZY1Y
10100X0
YZY1YYY
101X010
Z5
000010X
Y1Y10YZ
1X1XX11
Y1Y1Z1Z
1X1X1X0
1YY1Z1Z
X11X1X0
11YYZ1Z
XX111X0
ZZZZ01Z
00000X0
0000X10
ZZ1ZY1Z
00X00X0
Z1ZZZZZ
0100101
-
YZ1ZY1Z
10X00X0
Z1YYZYZ
0X11111
YZYZY0Z
10100X0
YZY1YYY
101X010
Z6
X0X00X0
Z1Z11ZY
1X1XX11
Z1Z1YZZ
1X1X1X0
ZYZ1YZZ
X11X1X0
Z1ZYYZZ
XX111X0
ZZZZZZZ
ZZZZ1ZZ
0000110
ZZZZZZZ
ZYZZYZY
0100101
-
Z1ZYYZY
0X11111
ZZZZZZZ
ZZZ1ZZZ
1011010
Z7
XX1111X
ZZZ00ZZ
1X10X11
1X1X011
ZZZ0Z0Z1X101X0
1X1X100
ZZZ0Z0ZX1101X0
X11X100
ZZYYZZZ
0000110
ZZYYZYZ
0100101
ZZ0YY0Z
10X00X0
-
ZZZZYZZ
1011010
Z7
ZZZZZ0Z
XX111001
Z8
X010XX0
Z1ZZZZY
1X10X11
Z1Z1ZZY
1Z1Z011
Z1ZZZZZ
11 01X0
Z1Z1ZZZ
111X100
1X11100
ZYZZZZZ
X1101X0
Z1ZYZZZ
XX11100
ZZYZZZZ
0000110
ZYYZZZY
0100101
ZZ0ZZZZ
10000X0
Z1ZYZZY
0X11111
-
ZZZYZZZ
1011010
Z9
101XX1X
Z1ZZZZZ
1110X11
Z1ZZZZZ
111X011
ZYZZZ0Z
11101X0
ZYZZZYZ
111X100
Z1ZZZYZ
1X11100
0YZZZ0Z
X1101X0
0YZZZYZ
X11X100
01ZZZYZ
XX11100
YZYZZZZ
0000110
YYYZZYZ
0100101
ZZYZZ0Z
10000X0
Y1ZZZZZ
0X11111
-
Z10
1X1X11X
ZZZZ0ZZ
1110011
111X011
ZZZZZ0Z
1110100
ZZZZZYZ
111X100
ZZZZZYZ
1X11100
0ZZZZ0Z
01101X0
X110100
0ZZZZY1
X11X100
0ZZZZYZ
XX11100
0000110
0100101
10000X0
0X11111
ZZZZYZZ
1011010
-
Полученное минимальное покрытие:
1X1XX11
XX1X1X0
00X0XX0
0X00101
X0X00X0
XX1111X
101XX1X
Cтоимость полученного покрытия равна 36 ( стоимость исходного покрытия равна 53 ).
ПОСТРОЕНИЕ ФАКТОРИЗОВАННОГО ПОКРЫТИЯ
Покрытие, полученное на основе простых импликант и выделения из них L-экстремалей, принято называть минимальным. Однако практика показывает, что дополнительная минимизация возможна при помощи факторизации. Таким образом, минимальным следует считать факторизованное покрытие, а не множество L-экстремалей.
Факторизация покрытия основана на операции -произведения, которая предназначена для выделения общей части двух кубов. Эта операция является поразрядной:
0 при ai = bi = 0, i = 1,n;
ai bi = 1 при ai = bi = 1, i = 1,n;
во всех остальных случаях.
Символ указывает координату исходных кубов, которая различна в них, либо есть Х.
Куб, в котором хотя бы одна координата является , называется -кубом и обозначается через е. Такой куб может участвовать в -произведении, тогда при умножении на координату должна получаться координата .
Стоимость для -куба определяется путем подсчета числа координат со значениями 0 и 1. Куб с наибольшей стоимостью считается максимальным. Если стоимость равна 0, то -куб считается пустым, он равен . Покрытие с учетом -куба записывается в несколько измененном виде: под -кубом фиксируются соответствующие ему кубы с сохранением тех координат, которые расположены под символами .
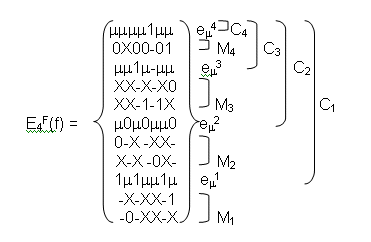
Алгоритм факторизации покрытия является циклическим. Количество циклов равно числу уровней разложения покрытия ( числу -кубов ). В разложенном по многим уровням покрытии выделяются на i-м цикле -куб еi, Mi ( множество кубов с прочерками, соответствующее еi ), Ci (множество кубов, которые будут рассматриваться на ( i+1)-м цикле).
Алгоритм факторизации можно сформулировать следующим образом:
Вычисляются -произведения всех пар из Сi-1. В первом цикле С0 = Е. Во втором цикле дело надо иметь с С1, в третьем – с С2 и т.д.
Выбирается -куб с наибольшей стоимостью еi. Если несколько кубов имеют одинаковую стоимость, то выбирается первый.
Покрытие оформляется разложенным на две части: нижнюю часть Мi и верхнюю часть Сi. Ci содержит оставшиеся от Сi-1 кубы после удаления из него кубов Мi и добавленный куб еi. Видимо,
Ci = ( Ci-1 – Mi ) ei.
Если Сi состоит из одного куба или получаются пустые -кубы, процесс факторизации следует закончить, в противном случае перейти к пункту 1.
Процесс факторизации по данному алгоритму удобно отражать в таблицах. Первый цикл представлен в табл. 9.
Первый цикл факторизации Таблица 9
e1
1X1XX11
e2
XX1X1X0
e3
00X0XX0
e4
0X00101
e5
X0X00X0
e6
XX1111X
e1
1X1XX11
-
e2
XX1X1X0
1
-
e3
00X0XX0
0
-
e4
0X00101
1
1
00
-
e5
X0X00X0
1
000
0
-
e6
XX1111X
11
11
1
-
e7
101XX1X
111
1
0
0
11
Из этой таблицы видно, что е1 = 111.. Покрытие после первого цикла выглядит следующим образом:
Так как С1 содержит больше одного куба, осуществляется переход ко второму циклу ( табл. 10 ).
Второй цикл факторизации Таблица 10
е2
XX1X1X0
е3
00X0XX0
е4
0X00101
е5
X0X00X0
е6
XX1111X
е2
XX1X1X0
-
е3
00X0XX0
0
-
е4
0X00101
1
00
-
е5
X0X00X0
0
000
0
-
е6
XX1111X
11
1
-
е1
111
1
11
Очевидно, что е2 = 000.
Покрытие после второго цикла факторизации выглядит следующим образом:
Так как С2 содержит больше одного куба, осуществляется переход к третьему циклу ( табл. 11 ).
Третий цикл факторизации Таблица 11
e2
XX1X1X0
e4
0X00101
e6
XX1111X
e2
XX1X1X0
-
e4
0X00101
1
-
e6
XX1111X
11
1
-
e2
000
0
0
Из таблицы 11 видно, что е3 = 11.
Покрытие после третьего цикла выглядит так:
Так как С3 содержит больше одного куба переходим к четвертому циклу (табл. 12).
Таблица 12
Четвертый цикл факторизации
e4
0X00101
е4
0X00101
-
е3
11
1
Ясно, что е4 = 1.
Факторизованное покрытие выглядит следующим образом:
Чтобы определить стоимость факторизованного покрытия, нужен соответствующий алгоритм. Его сущность можно изложить следующим образом:
определить стоимость рассматриваемого куба покрытия;
если куб является маскирующим (-куб), то добавить к стоимости 2;
если куб является обычным, то при Si > 1 добавить к стоимости 1, в противном случае ( Si = 1 ) добавлять 1 не нужно;
полученные стоимости кубов с добавлениями сложить.
В полученном выше факторизованном покрытии 11 кубов, его стоимость составляет 30. До факторизации стоимость покрытия составляла 36.
СОСТАВЛЕНИЕ ЛОГИЧЕСКОЙ СХЕМЫ НА ОСНОВЕ ДАННОГО БАЗИСА ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ
По любому кубическому покрытию можно построить логическую схему. По факторизованному покрытию схема строится следующим образом. Обычные кубы отражаются на схеме как элементы & с числом входов, равным стоимости куба. Прочеркнутые координаты на вход этих элементов не подаются. Они учитываются в маскирующих кубах в качестве общих сомножителей. Выходные сигналы обычных кубов, расположенных под рассматриваемым -кубом, суммируются, затем логическая сумма этих кубов подается на вход маскирующего куба, который отображается на схеме как элемент &. Логическая схема в булевом базисе, построенная по факторизованному покрытию, показана на рис.1.
Стоимость кубов М1 и М2,а также куба ХХ-Х1Х-, входящего в М3, равна 1. Поэтому соответствующие им переменные подаются непосредственно на входы элементов ИЛИ (12, 11 и 10 соответственно). Умножение на координаты куба е1 производится в элементе 15, на координаты куба е2 – в элементе 14, на координаты куба е3 – в элементе 13. Кубы е3 и е4 имеют общую пятую координату. Поэтому выходной сигнал элемента 13, соответствующего е3, логически суммируется с выходным сигналом элемента 8, а затем логическая сумма поступает на вход элемента 16, где происходит умножение на координаты куба е4.
Стоимость данной логической схемы равна 30, такова стоимость и факторизованного покрытия. Таким образом, можно сделать предварительное заключение о соответствии составленной схемы факторизованному покрытию.
Рис. 1
Дальше необходимо составить схему в универсальном базисе элементов, который в настоящее время широко применяется. Универсальный базис элементов – это система элементов, реализующая функцию И-НЕ или ИЛИ-НЕ.
Логическую схему на основе заданного универсального базиса легче всего построить по логической схеме на элементах булевого базиса элементов. Для этого нужно воспользоваться соответствием между элементами булевого базиса и заданного универсального базиса ( табл. 13 ). В данном случае используется базис ИЛИ-НЕ.
Таблица 13
Булевой
Базис
Универсальный базис ИЛИ-НЕ
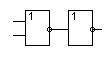
Заменяя элементы, не следует стремиться к полной замене. Если производить замену формально ( один к одному ), то в связи между элементами окажется два последовательно включенных инвертора, что равносильно их отсутствию.
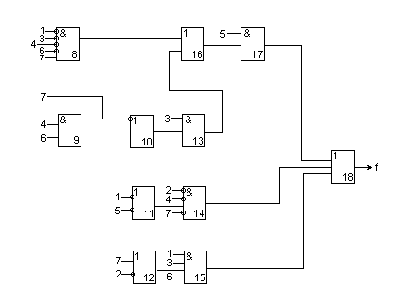
Логическая схема на основе элементов базиса ИЛИ-НЕ показана на рис.2.
функция покрытие логический кубический
Рис. 2
НАХОЖДЕНИЕ ПО ПИ-АЛГОРИТМУ РОТА ЕДИНИЧНОГО ПОКРЫТИЯ
Построенную логическую схему нужно проверить, для этого находится покрытие схемы. В табл. 15 отражено покрытие схемы, представленной на рис. 2. При нахождении покрытия схемы используются покрытия отдельных элементов схемы ( табл. 14 ).
Таблица 14
Элемент
Таблица истинности
Покрытие
ИЛИ
1 2 3
0 0 0
0 1 1
1 0 1
1 1 1
1 2 3
0 0 0
Х 1 1
1 Х 1
И
0 0 0
0 1 0
1 0 0
1 1 1
Х 0 0
0 Х 0
1 1 1
ИЛИ-НЕ
0 0 1
0 1 0
1 0 0
1 1 0
0 0 1
Х 1 0
1 Х 0
Обозначения: 1,2 – входы, 3 – выход элементов.
Таблица 15
1 2 3 4 5 6 7
8 9 10 11 12 13 14 15 16 17 18 19
Примечания
Х Х Х Х Х Х Х
Х Х Х Х Х Х Х Х Х Х Х 1
С(f)
0 1
П191 18
0 1
Пересечение с (Сf) ()
Х Х 1 0 1
Х 1 Х 0 1
1 Х Х 0 1
П180 14, 15, 17
Х Х 1 0 1
Х 1 Х 0 1
1 Х Х 0 1
Пересечение с () ()
1
Х Х 0 1 0 1
П171 5, 16
1
1
1
Х Х 0 1 0 1
Х 1 0 1 0 1
1 Х 0 1 0 1
Пересечение с () ()
Х 1 Х Х 0 1 0 1
1 Х Х Х 0 1 0 1
П160 8, 13
1
1
1
1
1
1
Х 1 Х Х 0 1 0 1
1 Х Х Х 0 1 0 1
Х 1 Х 1 0 1 0 1
1 Х Х 1 0 1 0 1
Х 1 1 Х 0 1 0 1
1 Х 1 Х 0 1 0 1
Пересечение с () ()
0 0 0 0 1
1 Х Х Х 0 1 0 1
П81 1, 3, 4, 6, 7
0 Х 0 0 1 0 1 0 Х 0 0 1 0 1
0 Х 0 0 1 0 1
0 Х 0 0 1 0 1
0 Х 0 0 1 0 1
0 Х 0 0 1 0 1
1 1 Х Х 0 1 0 1
1 Х Х Х 0 1 0 1
1 1 Х 1 0 1 0 1
1 Х Х 1 0 1 0 1
1 1 1 Х 0 1 0 1
1 Х 1 Х 0 1 0 1
Пересечение с () ()
1
Х 0 1 Х Х 0 1 0 1
П131 3, 10
1 1
1 1
1 1
1 1
1 1
1 1
Х 0 1 Х Х 0 1 0 1
1 0 1 Х Х 0 1 0 1
Х 0 1 Х 1 0 1 0 1
1 0 1 Х 1 0 1 0 1
Х 0 1 1 Х 0 1 0 1
1 0 1 1 Х 0 1 0 1
Пересечение с () (’)
Х Х Х Х Х Х Х
Х Х Х Х Х Х 0
Х 1 0 1 Х Х 0 1 0 1
Х Х 0 1 Х Х 0 1 0 1
П100 7, 9
Х Х 1 Х 1 Х Х
Х Х 1 Х 1 Х 0
Х Х 1 Х 1 Х Х
Х Х 1 Х 1 Х 0
Х Х 1 Х 1 Х Х
Х Х 1 Х 1 Х 0
Х Х 1 Х 1 Х Х
Х 1 0 1 Х Х 0 1 0 1
Х Х 0 1 Х Х 0 1 0 1
1 1 0 1 Х Х 0 1 0 1
1 Х 0 1 Х Х 0 1 0 1
Х 1 0 1 Х 1 0 1 0 1
Х Х 0 1 Х 1 0 1 0 1
1 1 0 1 Х 1 0 1 0 1
Пересечение с (’) ()
1 2 3 4 5 6 7
8 9 10 11 12 13 14 15 16 17 18 19
Примечания
Х Х 1 Х 1 Х 0
Х Х 1 Х 1 Х Х Х Х 1 Х 1 Х 0
Х Х 1 Х 1 Х Х
Х Х 1 Х 1 Х 0
1 Х 0 1 Х 1 0 1 0 1
Х 1 0 1 1 Х 0 1 0 1 Х Х 0 1 1 Х 0 1 0 1
1 1 0 1 1 Х 0 1 0 1
1 Х 0 1 1 Х 0 1 0 1
Пересечение с (’) ()
Х Х Х 1 Х 1 Х
Х 1 0 1 Х Х 0 1 0 1
П91 4, 6
Х Х 1 1 1 1 Х
Х Х 1 1 1 1 0
Х Х 1 1 1 1 Х
Х Х 1 1 1 1 0
Х Х 1 1 1 1 Х
Х Х 1 1 1 1 0
Х Х 1 1 1 1 Х
Х Х 1 1 1 1 0
Х Х 1 1 1 1 Х
Х Х 1 1 1 1 0
Х Х 1 1 1 1 Х
Х Х 1 1 1 1 0
Х 1 0 1 Х Х 0 1 0 1
Х 1 0 1 Х Х 0 1 0 1
1 1 0 1 Х Х 0 1 0 1
1 1 0 1 Х Х 0 1 0 1
Х 1 0 1 Х 1 0 1 0 1
Х 1 0 1 Х 1 0 1 0 1
1 1 0 1 Х 1 0 1 0 1
1 1 0 1 Х 1 0 1 0 1
Х 1 0 1 1 Х 0 1 0 1
Х 1 0 1 1 Х 0 1 0 1
1 1 0 1 1 Х 0 1 0 1
1 1 0 1 1 Х 0 1 0 1
Пересечение с () ()
0 0 0
0 1 Х 0 Х 0 1
П141 2, 4, 7, 11
0 0 0
0 0 0
0 0 0
0 1 Х 0 Х 0 1
0 1 Х 0 1 0 1
0 1 1 0 Х 0 1
Пересечение с () (’)
Х Х Х Х 0 Х Х
0 Х Х Х Х Х Х
0 1 Х 0 Х 0 1
0 1 Х 0 Х 0 1
П110 1, 5
Х 0 Х 0 0 Х 0
0 0 Х 0 Х Х 0
Х 0 Х 0 0 Х 0
0 0 Х 0 Х Х 0
Х 0 Х 0 0 Х 0
0 0 Х 0 Х Х 0
0 1 Х 0 Х 0 1
0 1 Х 0 1 0 1
0 1 1 0 Х 0 1
0 1 Х 0 Х 0 1
0 1 Х 0 1 0 1
0 1 1 0 Х 0 1
Пересечение с (') (’)
1 1 1
0 Х 1 0 Х 0 1
П151 1, 3, 6, 12
1 1 1
1 1 1
1 1 1
0 Х 1 0 Х 0 1
0 Х 1 0 1 0 1
0 1 1 0 Х 0 1
Пересечение с () (’’)
Х Х Х Х Х Х 1
Х 0 Х Х Х Х Х
0 Х 1 0 Х 0 1
0 Х 1 0 Х 0 1
П120 2, 7
1 Х 1 Х Х 1 1
1 0 1 Х Х 1 Х
1 Х 1 Х Х 1 1
1 0 1 Х Х 1 Х
1 Х 1 Х Х 1 1
1 0 1 Х Х 1 Х
0 Х 1 0 Х 0 1
0 Х 1 0 1 0 1
0 1 1 0 Х 0 1
0 Х 1 0 Х 0 1
0 Х 1 0 1 0 1
0 1 1 0 Х 0 1
Пересечение с (’') (’’)
Как следует из табл. 15, ищется покрытие схемы, обеспечивающее единичное значение выходной функции. Это означает, что на выходе элемента 19 должна быть единица (соответственно, на выходе элемента 18 должен быть 0). По табл. 15 можно увидеть что значение 0 на выходе элемента 18 будет, если на выходе хотя бы одного из элементов 14, 15, или 17 будет 1. Далее осуществляется пересечение покрытия элемента 18 с покрытием элемента 19. Затем последовательно фиксируются покрытия и пересечения применительно к элементам 17, 14 и 15. Результаты пересечения покрытий отмечаются «звездочками».
Покрытие схемы осуществляется по ветвям. После покрытия элементов первого яруса находятся кубы множества L-экстремалей Z. В табл. 15 эти кубы выделены подчеркиванием.
Для большей наглядности выпишем эти кубы:
0X00101
XX1X1X0
XX1111X
X0X00X0
00X0XX0
1X1XX11
101XX1X
Это найденное покрытие точно совпадает с ранее полученным покрытием Е. Следовательно, факторизация минимального покрытия и построение логической схемы осуществлены верно.
Далее необходимо произвести изменение схемы с учетом конкретных характеристик элементов данного универсального базиса, а именно Квх (коэффициент входа) и Кр (коэффициент разветвления). Современные элементы имеют сравнительно большие значения Квх и Кр, но в данном случае они выбраны малыми: Квх = 4; Кр = 2.
Применительно к схеме на рис. 2 можно сказать что нарушений по Квх нет, но нарушено требование по Кр в двух случаях. Измененная схема представлена на рис. 3. На ней помимо элементов 15, 16, 17 и 18, исправляющих нарушения по Кр, имеются инверторы для каждой координаты куба.
Вместо 19 элементов на рис. 2 стало 32 элемента на рис. 3.
СИНТЕЗ КОНТРОЛИРУЮЩЕГО ТЕСТА. КОНТРОЛЬ СХЕМЫ ТЕСТОМ
Синтезировать контрольный тест для логической схемы – найти множество кубов, которые позволяют выявлять неисправности схемы. Если в схеме нет неисправностей, то на каждом кубе получается так называемая эталонная реакция схемы. Множество кубов порождает множество эталонных реакций схемы.
При наличии неисправности в схеме реакция хотя бы на одном кубе должна измениться. В итоге множество реальных реакций не совпадает с множеством эталонных реакций. Это будет говорить о том, что неисправность выявляется. Если тест позволяет выявлять любую неисправность, то он обладает 100-процентной полнотой. Однако, это не всегда бывает так. Обычно тест не обеспечивает выявление всех неисправностей, его полнота менее 100%.
В данной курсовой работе рассматривается ограниченный класс неисправностей:
1). Выход элемента тождественно равен 0,
2). Выход элемента тождественно равен 1.
Считается, что в данный момент времени в схеме может быть только одна неисправность. Это означает, что схема является высоконадежной.
Синтез теста осуществляется по методу активизации пути. Сущность этого метода заключается в том, что, задав какую-либо неисправность на выбранном входе схемы, нужно обеспечить условия для беспрепятственного прохождения сигнала, связанного с заданной неисправностью, на выход схемы. Это означает, что при прохождении указанного сигнала через элемент ИЛИ-НЕ на всех других его входах надо обеспечить нули. В свою очередь обеспечение таких входных сигналов связано с выбором подходящей строки покрытия элемента, с которого снимается нужный сигнал.
Рис. 3
Процесс активизации путей схемы (рис.3) отображен в табл. 16. Всего оказалось 20 путей.
Контролирующий тест Таблица 16
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
Пути
1 0 0 0 1 1 0
0’1 1 1 0 0 1
1 0 1 0 0 0 1’ 0 1 0 0’ 0 0 0 1 0 1’ 0’
1, 8,21, 25, 31,32
1 0 1 1 0 1 0
0’1 0 0 1 0 1
0 1 1 0 0 1 0 0 1 0 0 1’ 0 1 0 0 0’ 1’
1, 8, 26, 31,32
1 1 0 0 1 0 1
0 0 1 1 0 1 0
1 0 0 1 0’ 0 1’ 0 1’ 1 0’ 0 0’ 0 1’ 0’ 1’ 0’
1, 19, 23, 27, 29, 30, 31, 32
1 1 1 0 0 1 0
0 0 0 1 1 0 1
1 0 1 0 0 0 0 1 1 0 0’ 0 0 1 0 0 1’ 0’
2, 25, 31, 32
1 1 1 0 0 1 0
0 0’ 0 1 1 0 1
1 0 1 0 0 0 0 1’ 1 0 0 0’ 0 1 0 0 1’ 0’
2, 9, 22,26, 31,32
0 1 1 0 1 0 1
1 0 0 1 0 1 0
1 0 0 1 0’ 0 0 0 1’ 1 0 0 0’ 0 1’ 0’ 1’ 0’
3, 19, 23, 27, 29, 30, 31, 32
0 1 1 0 1 1 0
1 0 0’ 1 0 0 1
1 0 1 0 0’ 0 0’ 1 1’ 0 0’ 0 0’ 1 0’ 1’ 0’ 1’
3, 10, 28, 29, 30, 31, 32
1 0 1 1 0 1 0
0 1 0’ 0 1 0 1
0 1 1 0 0 1 0 0 1 0 0 1’ 0 1 0 0 0’ 1’
3, 10, 26, 31, 32
0 1 0 1 1 0 1
1 0 1 0 0 1 0
0’ 1’ 0 1 0’ 0 0 0 1’ 1 0 0 0 0 1’ 0’ 1’ 0’
4, 15, 16, 19, 23, 29, 30, 31,32
1 0 0 1 0 1 0
0 1 1 0 1 0 1
0’ 1’ 1 0 0 1 0 0 1 0 0’ 0 0 0 1 0 1’ 0’
4, 15,16,25,31,32
0 0 1 1 1 1 0
1 1 0 0’ 0 0 1
0 1 1 0 0 1’ 0 0 1 0’ 0 0 0 1’ 0’ 1’ 0’ 1’
4, 11, 20, 24, 28, 29, 30, 31, 32
1 0 0 0 1 1 0
0 1 1 1 0’ 0 1
1 0 1 0 0 0 1’ 0 1 0 0’ 0 0 0 1 0 1’ 0’
5,12,21,25, 31,32
0 0 1 1 1 1 0
1 1 0 0 0’ 0 1
0 1 1 0 0 1 0 0 1 0 0 0 0 1 0 1’ 0’ 1’
5, 12, 30, 31, 32
0 1 0 0 1 1 1
1 0 1 1 0 0 0
1 0 0 1 0’ 0 0 0 1’ 1 0 0 0’ 0 1’ 0’ 1’ 0’
6,19,23,27,29,30,31,32
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
Пути
0 0 1 1 0 1 1
1 1 0 0 1 0’ 0
0 1 0 1 0 1’ 0 0 1 0’ 0 0 0 1’ 0’ 1’ 0’ 1’
6, 13, 20, 24, 28, 29, 30, 31, 32
1 0 1 1 0 1 0
0 1 0 0 1 0’ 1
0 1 1 0 0 1 0 0 1 0 0 1’ 0 1 0 0 0’ 1’
6, 13, 26, 31, 32
1 1 1 0 0 1 1
0 0 0 1 1 0 0
1 0 0’ 0’ 0 0 0 0’ 1 1 0 1’ 0 0 1 0 0’ 1’
7, 17, 18, 22, 26, 31, 32
0 0 1 0 1 1 1
1 1 0 1 0 0 0
1 0 0’ 1’ 0 0 0 0 1 1 0’ 0 0 0 1 0 1’ 0’
7,17,18,25,31,32
0 0 1 0 1 0 1
1 1 0 1 0 1 0’
1 0 0 1 0 0 0 0 1 1’ 0 0 0 0’ 1’ 0’ 1’ 0’
7, 14, 24, 28, 29, 30, 31, 32
0 1 0 0 1 0 1
1 0 1 1 0 1 0’
1 0 1 0 1 0 0 0 0 1 0 0 1’ 0 0’ 1’ 0’ 1’
7, 14, 27, 29, 30, 31, 32
После заполнения всех строк таблицы из нее следует выписать наборы входных переменных с соответствующими реакциями. При этом один набор с переменной 1’ распадается на два набора, в одном из них 1’ дает 1, а в другом – 0. В общей системе наборов обычно получаются одинаковые наборы. Лишние нужно удалить. Оставшиеся ( табл. 17 ) наборы с эталонными реакциями и являются тестом.
Таблица 17
Реакция
Наборы
Реакция
Наборы
0
0 0 1 1 0 1 1
0
0 0 1 0 1 1 1
1
1 0 1 1 0 1 0
0
0 0 1 0 1 0 1
0
1 1 0 0 1 0 1
1
0 1 0 0 1 0 1
0
1 1 1 0 0 1 0
1
0 0 0 0 1 1 0
0
0 1 1 0 1 0 1
0
0 0 1 1 0 1 0
1
0 1 1 0 1 1 0
1
1 0 1 0 0 1 0
0
0 1 0 1 1 0 1
1
1 0 0 0 0 1 0
0
1 0 0 1 0 1 0
0
0 0 1 1 0 0 1
1
0 0 1 1 1 1 0
0
1 0 1 1 0 0 0
0
0 1 0 0 1 1 1
1
0 0 1 0 1 1 0
1
0 0 1 1 0 1 1
1
0 0 1 0 1 0 0
1
1 1 1 0 0 1 1
0
0 1 0 0 1 0 0
Всего получилось 24 набора.
Чтобы проверить схему, надо задать три неисправности: одна касается какого-либо элемента ближе ко входам схемы, другая – к середине схемы, третья – к выходу схемы.
Надлежит установить, обнаруживается или нет каждая заданная неисправность тестом. При этом нужно брать те тестовые наборы, которые как раз и предназначены для обнаружения заданной неисправности.
Проверка схемы проведена в табл. 18. В соответствующем столбце фиксируется ошибка, сведения для столбцов, расположенных левее, берутся из табл.16, остальные заполняются самостоятельно с учетом введенной ошибки. Полученная реакция сравнивается с эталонной. Таким образом устанавливается, обнаруживается или нет заданная неисправность.
Проверка логической схемы контролирующим тестом Таблица 18
№ набора
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
Эталонная реакция
Пути
7
0 1 1 0 1 1 0
1 0 1 1 0 0 1
Выход 10 = 1
1 0 1 0 0 0 0 1 1 0 0 0 0 0 1 0 1 0
1
3, 10, 28, 29, 30, 31, 32
9
0 1 0 1 1 0 1
1 0 1 0 0 1 0
Выход 19 = 1
0 1 0 1 1 0 0 0 0 1 0 0 1 0 0 1 0 1
0
4, 15, 16, 19, 23, 27, 29, 30, 31,32
11
0 0 1 1 1 1 0
1 1 0 0 0 0 1
Выход 28 = 0
0 1 1 0 0 1 0 0 1 0 0 0 0 0 1 0 1 0
1
4, 11, 20, 24, 28, 29, 30, 31, 32
ЗАКЛЮЧЕНИЕ
В данной работе я выполнил синтез логической схемы по заданному в кубической форме покрытию. При этом мною предварительно была проведена минимизация и факторизация покрытия. Первоначальная стоимость покрытия была равна 48, после нахождения множества простых импликант она увеличилась на 5 (что составило 10,4% от первоначальной стоимости), после нахождения множества L-экстремалей стоимость уменьшилась на 17 (32%), а после проведения факторизации покрытия еще на 6 (16,7%). Итоговая стоимость покрытия получилась равной 30. Синтез схемы осуществлялся мною последовательно: сначала была построена схема в булевом базисе, затем по этой схеме была построена схема в универсальном базисе ИЛИ-НЕ (при этом использовались соответствия между элементами булевого и универсального базисов). После составления схемы в универсальном базисе была проведена проверка схемы путем нахождения единичного покрытия. Так как в ходе проверки были найдены все кубы множества L-экстремалей, то схема была признана правильной. И наконец, была составлена схема с учетом реально имеющихся ограничений, а именно: Квх и Кр. Обычно эта схема получается довольно громоздкой (до 50 и более элементов), но в моем случае Квх был равен 4, из-за чего схема увеличилась лишь незначительно: если в схеме в универсальном базисе было 19 элементов, то в конечной схеме их было только 32. Напоследок мною был синтезирован контролирующий тест и проведена проверка схемы тестом, которая показала, что заданная неисправность успешно обнаруживается тестом.
ЛИТЕРАТУРА
Триханов А.В. Синтез логических схем. Учебное пособие.-Томск,2007.
Майоров С.А. и др. Проектирование ЦВМ. – М.:ВШ,2006.
Миллер Р. Теория переключательных схем. Том 1. – М.:Наука,2006.
Триханов А.В. Алгоритмизация и микропрограммирование операций ЭВМ (множества, графы, кубы, кубические покрытия). Учебное пособие. – Томск: Изд-во ТПУ,2005.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ