Теория информации













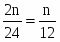
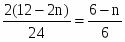
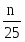
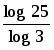

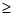
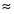
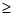
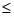
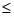
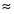

Ученица 10 А класса ГОУ РМЭ ЦО № 18
Коробкова Анна
г. Йошкар-Ола, 2004
Введение. Понятие энтропии.
Понятие информации.
Решение некоторых типовых задач.
Заключение
Список использованной литературы.
Главным свойством случайных событий является отсутствие полной уверенности в их наступлении, создающее известную неопределённость при выполнении связанных с этими событиями опытов. Однако совершенно ясно, что степень этой неопределённости в различных случаях будет совершенно разной. Возникновение математической теории информации стало возможным после того, как было осознанно, что количество информации можно задать числом.
Для практики очень важно уметь численно оценивать степень неопределённости самых разнообразных опытов. Начнём с рассмотрения опытов, имеющих к равновероятных исходов. Очевидно, что степень неопределённости каждого такого опыта определяется числом к: если при к=1 исход опыта вообще не является случайным, то при большом к предсказать исход опыта очень и очень сложно. Таким образом, искомая численная степень неопределённости должна являться функцией числа к, при к =1 обращаться в нуль и возрастать при возрастании числа к.
Теперь рассмотрим два независимых опыта А и В. Пусть опыт А имеет к равновероятных исходов, а опыт В – равновероятных исходов. Очевидно, что степень неопределённости двойного опыта АВ равна сумме степеней неопределённости опытов А и В. А так как опыт АВ имеет ks равновероятных исходов, приходим к следующему условию, которому должна удовлетворять наша функция f(k):
f(ks)=f(k)+f(s).
Это условие наталкивает на мысль принять за меру неопределённости опыта, имеющего к равновероятных исходов, число log k, так как логарифмическая функция – единственная, удовлетворяющая всем вышеперечисленным условиям. Заметим, что выбор основания системы логарифмов здесь несуществен, так как в силу известной формулы
logbk = logbalogak
переход от одной системы логарифмов к другой сводится лишь к простому изменению единицы измерения степени неопределённости. Как правило, используются логарифмы при основании 2. Такая единица измерения называется двоичной единицей или битом.
Общая неопределённость опыта, имеющего к исходов, равна сумме неопределённостей, вносимых каждым исходом. Это число называют энтропией опыта А, будем его обозначать через Н(А). Рассмотрим некоторые свойства энтропии. Прежде всего, она не может принимать отрицательные значения: т.к. всегда
0 ≤ p(A) ≤ 1, то log p(A) не может быть положительным, а – p(A) log p(A) – отрицательным (р(А) – вероятность получения исхода А в опыте). Также заметим, что если р очень мало, то и произведение – p(A) log p(A) тоже будет весьма малым, хотя и положительным, т.е. при р произведение – p log p неограниченно убывает. Энтропия опыта равна нулю, когда один из его исходов имеют степень вероятности 1, а остальные – степень вероятности 0. Наибольшую энтропию имеет опыт с равновероятными исходами.
Пусть какое-либо измерение или наблюдение Б, предшествующее опыту А, может ограничить количество возможных исходов опыта А и тем самым уменьшить степень его неопределённости. Для того, чтобы результат Б сказался на последующем опыте А, нужно, чтобы его результат не был известен заранее; поэтому Б можно рассматривать как вспомогательный, также имеющий несколько допустимых исходов. При этом, если опыт А не зависит от опыта Б, то осуществление Б не уменьшает энтропии А; если же наоборот результат Б полностью предопределяет исход А, то энтропия А уменьшается до 0.
Таким образом, разность
I(A,Б)= H(A) – Hб(A)
указывает, насколько осуществление опыта Б уменьшает неопределённость А. Эту разность называют количеством информации относительно опыта А, содержащемся в опыте Б, или, короче, информацией о А, содержащейся в Б. Таким образом, мы получаем возможность численного изменения информации.
Часто может случиться, что, желая узнать исход какого-либо опыта А, мы можем с этой целью по-разному выбирать опыты Б. В этом случае всегда рекомендуется начинать с того опыта Б0, который содержит наибольшую информацию относительно А, так как при другом опыте Б мы вероятно добьемся менее значительного уменьшения степени неопределённости А. Реально же, конечно, может получиться и наоборот.
Также необходимо заметить, хотя это и не относится к той части теории, которая пригодится нам для решения задач, что информация имеет ярко выраженный материальный характер — то есть она может передаваться только с помощью вещества или энергии.
Пусть известно, что житель некоторого города А всегда говорят правду, а жители соседнего города Б всегда обманывают. Наблюдатель Н. знает, что он находится в одном из этих двух городов, но не знает, в каком именно. Путём опроса встречного ему требуется определить, в каком городе он находится, или в каком городе живёт его собеседник (жители А могут заходить в Б и наоборот), или то и другое вместе. Спрашивается, каково наименьшее число вопросов, которые должен задать Н. (на все вопросы встречные отвечают лишь да или нет)?
Пусть Н. надо определить, в каком городе он находится. Здесь опыт А может иметь 2 равновероятных исхода. Энтропия Н(А) опыта А равна одному биту. Далее, опыт Б в составе одного вопроса, также может иметь два исхода, поэтому энтропия Н(Б) самое большее равна одному биту. Следовательно, можно надеяться, что при удачно поставленном вопросе Б будет иметь место равенство
I(Б,А) = Н(А)
Для этого только необходимо, чтобы оба ответа на вопрос Б были равновероятны, и исход Б полностью определял результат А. Всем этим условиям удовлетворяет вопрос «Живёте ли вы в этом городе?» (положительный ответ может быть дан только в городе А, а отрицательный – в Б).
Ещё проще узнать, в каком городе живёт его собеседник – для этого достаточно задать какой-нибудь вопрос, ответ на который Н. знает заранее (например, равно ли дважды два четырём?).
Если же Н. должен узнать ответы на оба вопроса, ему предстоит определить исход сложного опыта А1А2. В этом случае он нуждается в информации, большей 1 бита. Таким образом, оценки количества информации дают нам строгое доказательство того, что за один вопрос выяснить, где находится Н. и откуда родом отвечающий. Для этого нужно как минимум 2 вопроса.
Сколько вопросов надо задать, чтобы отгадать задуманное число, не превосходящее 10, если спрашиваемый отвечает на вопросы лишь «да» и «нет»?
Опыт А, состоящий в выяснении задуманного числа, может иметь 10 различных исходов. До ответа на первый вопрос все эти исходы можно считать равновероятными, так что энтропия Н(А) опыта А равна log 10 3,32 бита. Рассмотрим сложный опыт Бк = б1б2б3…бк, заключающийся в том, что спрашивающий задаёт к вопросов. Для того чтобы исход опыта Бк полностью определял исход А, необходимо, чтобы имело место равенство I (Бк, А) = Н (А). Отсюда:
log 10 = Н (А) = I (Бк, А) Н (Бк) к
то есть
к log 10 3,32
или, так как к - целое число,
к 4.
Теперь рассмотрим, какие вопросы выгоднее всего задавать. Во-первых, нужно, чтобы энтропия была возможно большей (то есть действительно равнялась одному биту), а значит оба варианта ответа должны быть равновероятны. Далее нужно, чтобы информация I(б1, А) относительно А, заключённая в б1, равнялась энтропии Н (б1) опыта б1, а не была бы меньше этой величины. Для этого надо, чтобы ответ на первый вопрос не содержал «посторонней» информации, то есть чтобы условная энтропия На (б1) равнялась нулю. Эти условия достаточно ясно указывают на то, как нужно поставить первый вопрос. Разобьём множество всех возможных значений нашей переменной (то есть множество целых положительных чисел от 1 до 10) на две равные по численности группы (так как исходы опыта б1 должны быть равновероятны) и спросим, относится ли задуманное число к одной или другой из них (например, больше ли оно пяти). Далее нужно разбивать оставшееся множество чисел на две возможно близкие по численности части, и тогда мы определим задуманное число с помощью четырёх вопросов. Нужно сказать, что с помощью тех же четырёх вопросов мы угадаем не только одно из 10 задуманных чисел, но даже одно из 16, так как после того как уже выяснено, что число имеет одно из Х значений, где Х нечётно, невозможно добиться строгой равновероятности исходов последующего опыта, следовательно, энтропия этого опыта будет меньше 1. Это означает, что наш опыт не особенно выгоден с точки зрения полученной информации, то есть что с помощью того же числа вопросов можно найти загаданное число, имеющее не одно из 10, а одно из 24 = 16 возможных значений.
Вообще, наименьшее число k вопросов, позволяющее найти заданное число Х, имеющее одно из n допустимых значений, определяется неравенствами
k – 1< log n ≤ k или 2k - 1 < n ≤ 2k.
Также можно заметить, что независимо от значения n
k ≥ log n;
при этом k = log n только в том случае, когда число n является целой степенью числа 2.
Имеется 25 монет одного достоинства; 24 из них имеют одинаковый вес, а одна – фальшивая – несколько легче остальных. Спрашивается, сколькими взвешиваниями на чашечных весах без гирь можно обнаружить эту фальшивую монету.
Опыт А, результат которого требуется определить, имеет в этом случае 25 возможных исходов, значит, так как эти исходы равновероятны, Н(Б) = log 25. Опыт б1, состоящий в одном взвешивании, может иметь 3 исхода (либо перевесит левая чашка, либо правая, либо веса останутся в равновесии); поэтому Н (б1) = log 3 и информация I(б1, А), получаемая при проведении такого опыта, не превосходит log 3. Рассмотрим теперь сложный опыт Бк = б1б2…бк, заключающийся в k последовательных взвешиваниях; он даёт информацию, не превосходящую k log 3. Если опыт Бк позволяет полностью определить исход опыта А, то должно выполняться
Н (Бк) ≥ I (Бк, А) ≥ Н (А) или k log 3 ≥ log 25.
Отсюда заключаем, что 3к ≥ 25, то есть
K ≥ log3 25 =
Или, так как k – целое число, k ≥ 3.
Нетрудно показать, что с помощью трёх взвешиваний всегда можно определить фальшивую монету. Предположим, что на каждую чашку весов нами положено по n монет, не положены на весы будут 25 - 2n монет. Так как вероятность того, что фальшивая монета окажется в данной группе из n монет, равна , то три исхода опыта б1 будут иметь наиболее близкие вероятности, если n = 8 и 25 - 2n = 9. При любом исходе опыта при втором взвешивании (опыт б2) на обе чашки весов следует положить по 3 монеты из определившейся после предыдущего опыта группы, а третьим взвешиванием мы из группы из трёх монет найдём фальшивую, положив по одной монете на обе чашки весов.
Имеется 12 монет одного достоинства; 11 из них имеют одинаковый вес, а одна – фальшивая – отличается по весу от остальных (причём неизвестно, легче она или тяжелее настоящих). Каково наименьшее число взвешиваний на чашечных весах без гирь, которое позволяет обнаружить фальшивую монету и выяснить, легче она, чем остальные монеты, или тяжелее?
Здесь рассматривается опыт А, имеющий 24 возможных равновероятных исхода. Энтропия Н (А) опыта А равна log 24. Таким образом, нам нужно получить log 24 единиц информации. Так как, произведя сложный опыт Ак = а1а2…ак, состоящий в k взвешиваниях, мы можем получить информацию, не большую, чем k log 3 = log 3, а 33 = 27, то с первого взгляда кажется ясным, что трёх взвешиваний будет достаточно.
Пусть при первом взвешивании мы положили на обе чашки по n монет. Если чашки весов при этом остались в равновесии, то фальшивой является одна из 12−2n отложенных монет, что отвечает 2(12−2n) исходам рассматриваемого опыта А (из общего числа 24 исходов). Если перевесила правая чашка, то либо фальшивой и более тяжёлой является одна из n «правых» монет, либо фальшивой и более лёгкой является одна из n «левых» монет − эти случаи отвечают 2n исходам А, точно так же, случаю, когда перевесила левая чашка, отвечают 2n исходов А. Таким образом, три исхода первого взвешивания имеют вероятности
, и .
Отсюда сразу следует, что наибольшую энтропию опыт будет иметь при n = 4, три исхода которого равновероятны. Далее рассмотрим отдельно 2 случая.
1). При первом взвешивании чашки весов остались в равновесии. В таком случае фальшивой является одна из четырёх отложенных монет. Нам надо при помощи двух взвешиваний определить, какая именно из них является фальшивой, и выяснить, легче она или тяжелее остальных; так как у нас осталось 2∙4 = 8 возможных исходов опыта А, а 2 log 3 = log 9 > log 8, то можно ожидать, что это возможно. Если, однако, положить на каждую чашку весов по одной монете, и они останутся в равновесии, то следующим опытом нам надо будет определить исход опыта, имеющего 4 возможных исхода, что невозможно. То же самое получится, если положить на каждую чашку по две монеты. Однако рано говорить, что трёх взвешиваний недостаточно для выполнения задачи – ведь у нас ещё остались заведомо настоящие монеты после завершения первого опыта. Обозначим через аm,n опыт, состоящий в том, что на правую чашку весов кладутся m из наших подозрительных монет, а на левую n ≤ m из этих монет и ещё m−n заведомо настоящих монет. Через р(Р), р(П) и р(Л) мы обозначим соответственно вероятности того, что при опыте аm,n чашки весов останутся в равновесии и что перетянет правая или левая чашка весов. Так как, очевидно, m + n ≤ 4, то все опыты аm,n легко перечислить: отвечающие им значения вероятностей р(Р), р(П) и р(Л) собраны в таблице, в которой также указана энтропия в битах Н(аm,n) опыта аm,n (равная − р(Р) log р(Р) − р(П) log р(П) − р(Л) log р(Л)).
m
n
р(Р)
р(П)
р(Л)
Н(аm,n)
1
1
0,5
0,25
0,25
1,50
1
0
0,75
0,125
0,125
1,06
2
2
0
0,5
0,5
1,00
2
1
0,25
0,375
0,375
1,56
2
0
0,5
0,25
0,25
1,50
3
1
0
0,5
0,5
1,00
3
0
0,25
0,375
0,375
1,56
4
0
0
0,5
0,5
1,00
Из этой таблицы видно, что наибольшую энтропию имеют опыты а2,1 и а3,0; поэтому для получения наибольшей информации следует воспользоваться ими. Нетрудно видеть, что в обоих случаях мы можем затем третьим взвешиванием полностью определить исход А.
2). При первом взвешивании одна из двух чашек весов (например, правая) перетянула. В таком случае, либо одна из четырёх «правых» монет является фальшивой и более тяжёлой, либо одна из четырёх «левых» − фальшивой и более лёгкой. При втором взвешивании мы можем на правую чашку весов положить n1 «правых» монет и n2 «левых», а на левую чашку − m1 «правых» монет, m2 «левых» и (n1 + n2) − (m1 + m2) заведомо настоящих из числа не участвовавших в первом взвешивании. Здесь тоже можно составить таблицу энтропий опытов а n1,n2;m1,m2 , однако, так как число всевозможных вариантов тут слишком велико, то некоторые из них целесообразно исключить с самого начала.
Заметим, что после двух взвешиваний у нас должно остаться не более трёх возможных исходов опыта А. Отсюда следует, что число сомнительных монет, не участвующих во втором взвешивании, не должно превосходить 3.
Перечислим теперь все случаи, удовлетворяющие этим условиям.
-
n1
n2
m1
m2
р(Р)
р(П)
р(Л)
Н(а n1,n2;m1,m2)
2
1
2
1
0,25
0,375
0,375
1,56
2
1
2
0
0,375
0,25
0,375
1,56
2
1
1
1
0,375
0,375
0,25
1,56
1
2
1
2
0,25
0,375
0,375
1,56
1
2
0
2
0,375
0,375
0,25
1,56
1
2
1
1
0,375
0,25
0,375
1,56
3
1
1
0
0,375
0,375
0,25
1,56
1
3
0
1
0,375
0,25
0,375
1,56
2
2
1
1
0,25
0,375
0,375
1,56
2
2
1
0
0,375
0,25
0,375
1,56
2
2
0
1
0,375
0,375
0,25
1,56
3
2
1
0
0,25
0,375
0,375
1,56
2
3
0
1
0,25
0,375
0,375
1,56
Таким образом, мы видим, что здесь имеется уже не два, как в предыдущем случае, а целых 13 вариантов второго опыта. Энтропия каждого из них достаточна, чтобы иметь возможность полностью определить исход А с помощью ещё одного, третьёго, взвешивания.
Значит, действительно трёх взвешиваний достаточно, чтобы ответить на поставленный в задаче вопрос.
Я думаю, излишне говорить о том, что теория информации имеет огромное значение для развития современной науки и техники. Она получила широкое применение в физике, микроэлектронике, а также во всех отраслях техники, где необходимо решать проблемы хранения, получения и передачи информации.
Список использованной литературы.
А. Реньи. «Записки студента теории информации».
А.М. Яглом, И.М. Яглом. «Вероятность и информация».

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ