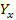
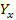
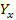
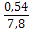
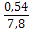
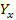
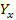
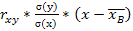
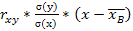
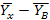
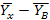
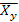
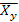
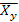
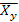
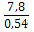
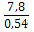
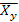
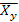
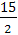
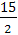
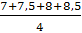
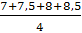
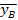
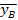
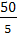
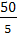
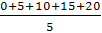
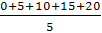
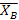
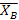
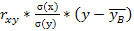
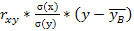
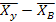
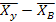
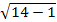
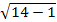
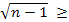
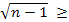
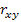
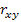
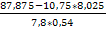
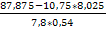
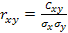
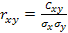
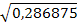
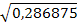
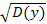
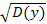
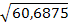
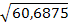
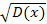
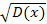
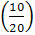
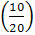
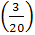
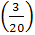
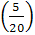
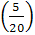
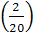
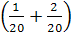
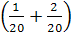
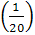
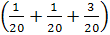
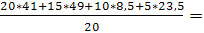
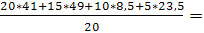
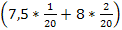
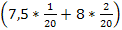
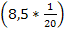
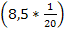
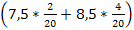
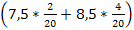
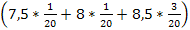
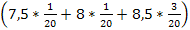
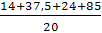
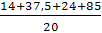
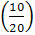
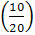
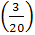
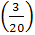
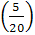
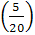
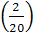
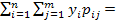
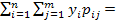
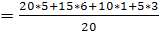
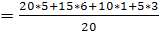
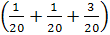
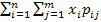
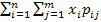
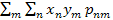
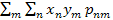
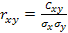
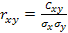
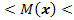
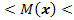
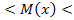
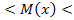
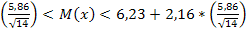
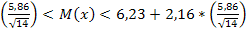
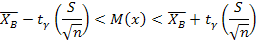
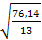
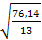
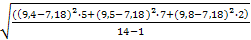
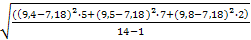
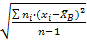
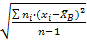
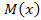
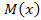
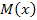
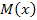
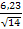
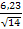
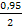
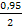
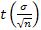
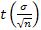
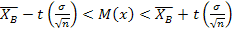
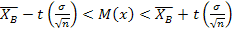
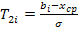
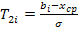
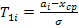
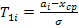
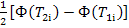
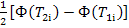
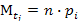
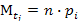
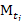
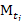
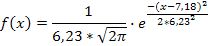
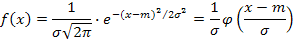
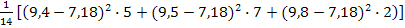
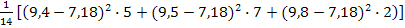
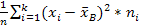
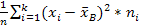
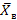
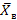
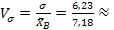
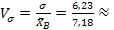
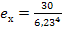
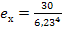
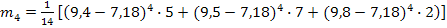
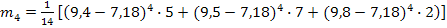
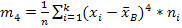
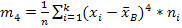
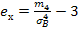
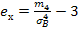
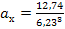
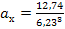
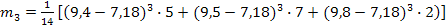
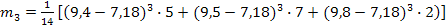
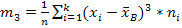
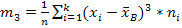
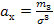
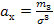
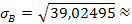
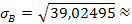
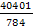
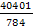
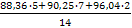
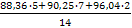
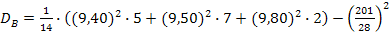
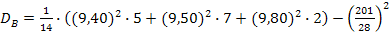
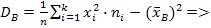
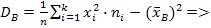
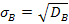
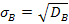
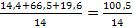
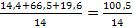
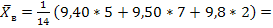
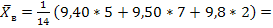
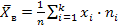
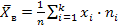
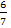
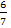
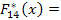
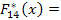
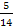
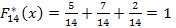
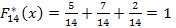
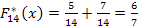
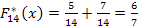
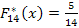
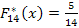
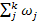
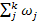
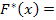
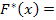
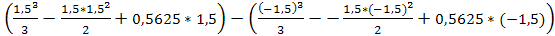
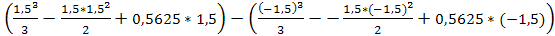
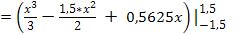
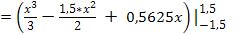
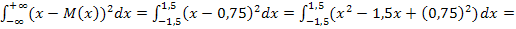
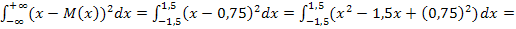
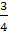
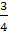
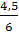
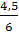
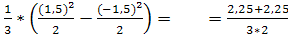
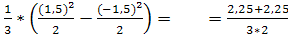
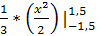
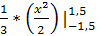
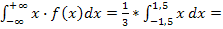
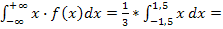
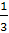
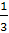
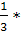
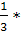
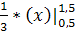
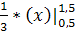
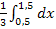
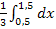
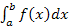
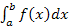
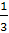
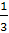
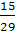
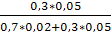
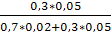
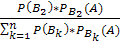
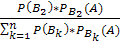
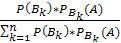
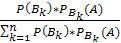
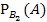
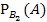
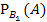
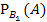
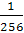
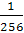
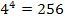
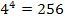
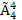
Министерство образования и науки

Российской Федерации

Федеральное агентство по образованию

Филиал государственного образовательного учреждения

Высшего профессионального образования

«Тюменский государственный университет»

В г. Тобольске

Специальность «Финансы и кредит»

Контрольная работа

Предмет: «Теория вероятности и математическая статистика»

Вариант №8

Выполнила:

№ зачетной книжки:

№ группы:

Домашний адрес:

Тобольск, 2009

1. На трех карточках написаны буквы У, К, Ж. После тщательного перемешивания берут по одной карточке и кладут последовательно рядом. Какова вероятность того, что получится слово «ЖУК»?

Решение

Вариант получившегося слова является размещением 3-х элементов по 3.

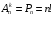
N(n-1)(n-2)…(n-k+2)(n-k+1)=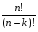

Отсюда получаем:

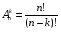
Число таких вариантов равно:

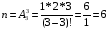
Из этих вариантов правильным будет только один, т.е. m=1, тогда по классическому определению вероятности

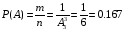
2. Какое из восьми вычислительных устройств обслуживается одним оператором? В штатном составе вычислительного центра имеется 6 операторов. Назначение оператора на данное вычислительное устройство производится наудачу. Найти вероятность того, что первые шесть вычислительных устройств будут обслужены.

Решение

Поскольку количество испытаний не велико (n=8), то для нахождения вероятности того, что событие А появится точно k=6 раз воспользуемся формулой Бернулли:

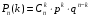, где q=1-p

По условию задачи вероятность назначения оператора равна 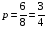, значит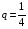

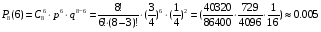
3. Опыт состоит в четырехкратном выборе с вращением одной из букв алфавита Е={а, б, о, м} и выкладывании слова в порядке поступления букв. Какова вероятность того, что в результате будет выложено слово «мама»?

Решение

Число элементарных исходов равно числу размещений с повторениями из четырёх элементов по четыре элемента, т.е.

N = =

Слову «мама» соответствует лишь один исход. Поэтому

Р(А) = = 0,00390625 ≈ 0,004

Ответ: 0,004.

4. 70% деталей, поступающих на сборку, изготовлены автоматом, дающим 2% брака, а остальные детали автоматом, дающим 5% брака. Наудачу взятая деталь оказалась бракованной. Какова вероятность того, что она изготовлена первым автоматом?

Решение

детали брак

1 автомат 70% 2%

2 автомат (100-70)% 5%

Введём обозначения для событий: А - взятая деталь оказалась бракованной; В₁, В₂ – эта деталь изготовлена соответственно первым и вторым автоматом. Имеем:

Р(В₁) = 0,7; Р(В₂) = 0,3

=0,02 = 0,05

По формуле Байеса Р_А(В_k) = (k = 1, 2, …, п) находим

Р_А(В₂) = = = ≈ 0,52

5. В первый класс должны были принять 200 детей. Определить вероятность того, что среди них окажутся 100 девочек, если вероятность рождения мальчиков равна 0,515.

Решение

Пусть событие А состоит в том, что в первый класс приняли 200 детей, девочек будет 100. Поскольку количество испытаний велико (n=200), то для нахождения вероятности того, что событие А появится ровно k=100 раз воспользуемся локальной теоремой Лапласса:

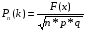, где 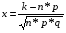и F(x) – диф. функция Лапласса-Гаусса.

По условию задачи вероятность рождения мальчиков равна q=0.515,значит

вероятность рождения девочек равна p=1-q=1-0.515=0.485

Определим аргумент функции Лапласса-Гаусса x:

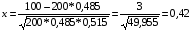
По таблице значений функций Лапласса определяем, что F(0,42)=0,1628

Теперь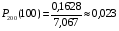

6. Случайная величина Х задана функцией f(x). Определить: а) плотность распределения f(x); b) вероятность попадания случайной величины Х в интервал (a,b); с) математическое ожидание и дисперсию этой случайной величины. Построить график функций F(x) и f(x).

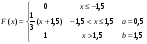
Решение

0 x ≤ -1,5

а) f(x) = F'(x) f(x) = -1,5 < x ≤ 1,5

0 x > 1,5

b) P (a ≤ x ≤ b) = =>

= > P (-1,5 ≤ x ≤ 1,5) = = = (1,5 - 0,5) = ≈ 0,33

c)М(х)= = = = ≈ 0,75

D(x)=
= = 3,9375 ≈ 4

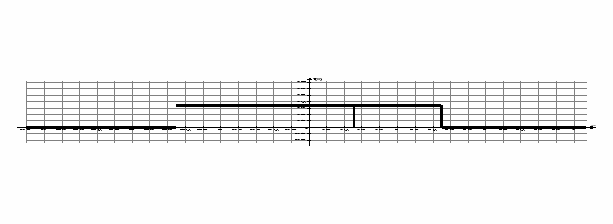
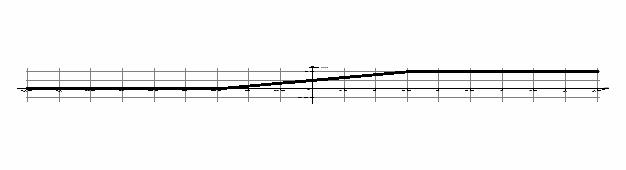
Построим графики F(x) и f(x)

7. Даны результаты наблюдений некоторой случайной физической величины Х, сгруппированные в статистический ряд.

а) Построить гистограмму и полигон частот.

b) Составить эмпирическую функцию распределения и изобразить ее графически.

с) Вычислить числовые характеристики:

1. выборочную среднюю;

2. выборочное среднее квадратичное отклонение;

3. асимметрию;

4. эксцесс;

5. коэффициент вариаций.

d) По виду гистограммы и полигона, а также по значению выборочных коэффициентов а_x и е_х и, исходя из механизма образования исследуемой случайной величины Х сделать предварительный выбор закона распределения случайной величины Х.

е) Определить точные оценки параметров нормального закона распределения а и b, предполагая, что исследуемая случайная величина распределена по нормальному закону, записать плотность распределения вероятностей f(x).

f) Найти теоретические частоты с нормальным законом с помощью основных критериев согласия – критерия Пирсона и критерия Колмагорова.

g) Найти интервальные оценки параметров нормального закона распределения (доверительную вероятность принять равной 0,95).

Время выполнения упражнения (с):

Границы интервалов

9,35-9,45

9,45-9,55

9,55-10,05

Частоты

5

7

2

Решение

Границы интервалов

9,35-9,45

9,45-9,55

9,55-10,05

Середины интервалов

9,40

9,50

9,80

Частоты

5

7

2

п = 14

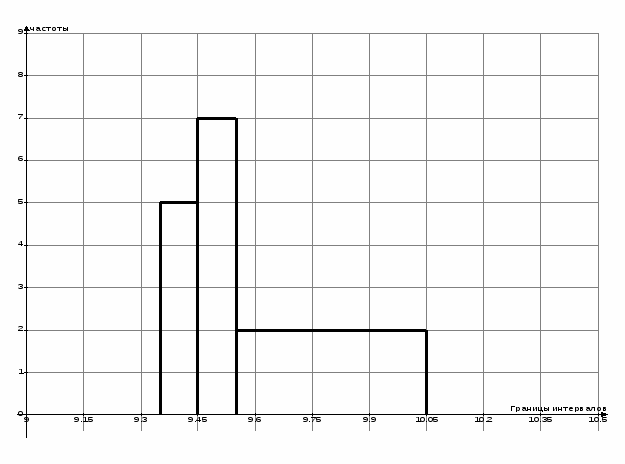
а) Построим гистограмму и полигон частот.

Гистограмма частот

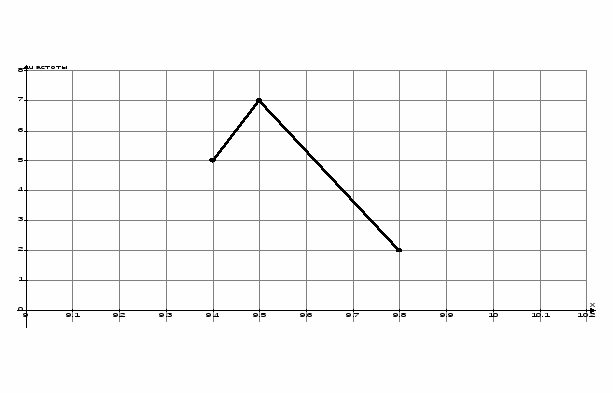
Полигон частот

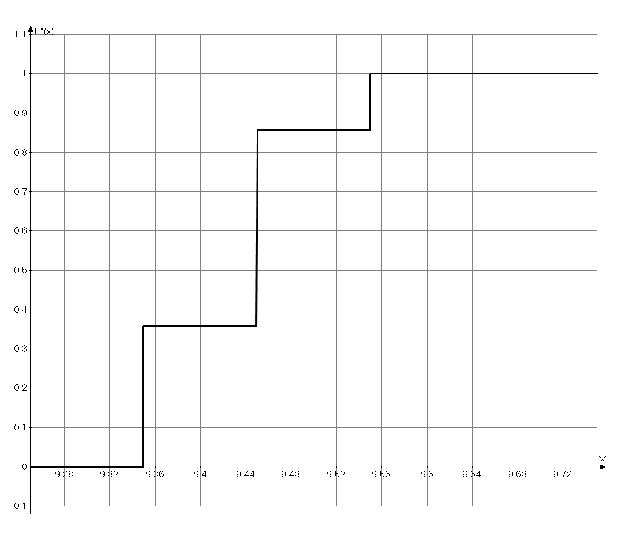
b) Составим эмпирическую функцию распределения и изобразим ее графически.

Найдём объём выборки: n = 5 + 7 + 2 = 14

Зная, что

0 при x < x₁

при x_k ≤ x ≤ x_k+1 (k € N)

1 при x ≤ x_s

, при 9,35 < x < 9,45

, при 9,45 < x < 9,55

, при 9,55 < x < 10,05

можем записать эмпирическую функцию и изобразить графически:

0 при х ≤ 9,35

при 9,35 < x < 9,45

, при 9,45 < x < 9,55

1 при 9,55 ≤ x

с) Вычислим числовые характеристики:

1. выборочную среднюю;

,

в данной задаче в качестве x_i возьмём серидины интервалов, а n_i – соответствующие этим интервалам частоты.

≈ 7,18

2. выборочное среднее квадратичное отклонение;

,

≈ - ≈ 38,87

6,23

3. асимметрию;

,

≈ 12,74

≈ 0,05

4. эксцесс;

,

≈ 30

-3 = -2,98017 ≈ -3

5. коэффициент вариаций.

0,87

d) По виду гистограммы и полигона, а также по значению выборочных коэффициентов а_x и е_х и, исходя из механизма образования исследуемой случайной величины Х сделать предварительный выбор закона распределения случайной величины Х.

Решение:

Сделаем предварительный выбор закона распределения случайной величины Х.

• а_x = 0,05 и е_х = -3, что неприемлимо для нормального закона распределения.

• М(х) = σ(х) – для показательного закона распределения. Здесь имеем М(х) = = 7,18, а
  σ(х) = 6,23 => отпадает версия о показательном распределении.

• При законе распределения Пуассона М(х) = D(х) = а. В данной задаче М(х) = 7,18, а

D(х)=d_B= = ≈
≈ 5,44 => и этот закон отпадает.

• Таким образом, сходя из механизма образования исследуемой случайной величины Х можно сделать вывод-предположение, что она распределена по биноминальному закону распределения.

е) Определим точные оценки параметров нормального закона распределения а и b, предполагая, что исследуемая случайная величина распределена по нормальному закону, запишем плотность распределения вероятностей f(x).

Предположим, что исследуемая случайная величина распределена по нормальному закону распределения, тогда параметр а – это математическое ожидание М(х), а параметр b – это среднее квадратичное отклонение σ(х).

Плотность распределения вероятностей f(x) будет выглядеть так:

а = М(х) = 7,18 , b = σ(х) = 6,23.

f) Найдём теоретические частоты с нормальным законом с помощью основных критериев согласия – критерия Пирсона и критерия Колмагорова.

При нахождении теоретических частот за оценку математического ожидания и среднего квадратического ожидания нормального закона распределения принимают значения соответствующих выборочных характеристик и σ_в , т.е.

m = = 7,18 , G = σ_в = 6,23

, где n – объём выборки, n = 14

р_i – величина попадания значения нормально распределённой случайной величины в i-ый интервал.

р_i = р (а_i < x ≤ b_i ) ≈ ,

,

a_i

b_i

n_i

T_1i

T_2i

1/2 Ф(T_1i)

1/2 Ф(T_2i)

p_i

p_i*n

M_ti

9,35

9,45

5

0,35

0,36

0,1847

0,19465

0,00995

0,04975

0,05

9,45

9,55

7

0,36

0,38

0,19465

0,2045

0,00985

0,06895

0,07

9,55

10,05

2

0,38

0,46

0,2045

0,24235

0,03785

0,0757

0,08

g) Найти интервальные оценки параметров нормального закона распределения (доверительную вероятность принять равной 0,95).

, γ = 0,95.

где = δ – точность оценки,

n – объём выборки,

t – значение аргумента функции Лапласа Ф(t) = = 0,475 => t = 1,96

δ = 1,96 * = 3,27

7,18 – 3,27 < < 7,18 + 3,27

3,91 < < 10,45

S = = = ≈ 5,86 ,

где S – исправленное среднее квадратическое отклонение

S( 1 - q) < σ < S( 1 + q) если q < 1

0 < σ < S( 1 + q) если q < 1

По данным задачи γ = 0,95 и n = 14 в специальном приложении найдём q = 0,48< 1. Итак:

6,23*( 1 – 0,48) < σ < 6,23*( 1 + 0,48)

3,2396 < σ < 9,2204

3,2 < σ < 9,2

Математическое ожидание найдём при неизвестном σ нормального распределения.

По таблице в специальном приложении к учебнику определим t_γ => t_γ = 2,16

6,23 – 2,16*

2,8535 9,6157

2,9 9,6

8. Зависимость между признаками X и Y задана корреляционной таблицей. Требуется:

а) вычислить выборочный коэффициент корреляции;

b) составить уравнение прямых линий регрессии X на Y и Y на X.

X – стрела кривизны рельса, см.

Y – количество дефектов рельса, см на 25 м.

Y

X

6,75-7,25

7,25-7,75

7,75-8,25

8,25-8,75

0

2

1

2

5

1

2

10

1

15

2

4

20

1

1

3

Решение

а) вычислим выборочный коэффициент корреляции;

, C_xy = M(xy) – M(x)M(y) , M(xy) =

Y

X

6,75-7,25

7,25-7,75

7,75-8,25

8,25-8,75

n_x

7

7,5

8

8,5

0

2

1

2

5

5

1

2

3

10

1

1

15

2

4

6

20

1

1

3

5

n_y

2

5

3

10

20

M(x) = m_x =

M(x) = m_x = 20* + 15* + 10* + 5* + 0 =
= 10,75

M(y) = m_y = 7* + 7,5* + 8* + 8,5* = = =8,025

M(xy) = 20*+ 15* +10* +
+ 5* = 87,875

D(x) = M(x²) – [M(x)]² = 20²*+15²*+10²*+5²*+ 0- -87,875² = 176,25 - 115,56 = 60,6875

D(y) = M(y²) – [M(y)]² = 7²* + 7,5²* + 8²* + 8,5²* - 8,025² = 64,6875 -
- 64,40063 = 0,286875

σ(х) = = ≈ 7,8

σ(y) = = ≈ 0,54

= = 0,384961383 ≈ 0,4

Если || * 3, то связь между случайными величинами x и y достаточно вероятна.

|0,4|* ≈ 1,39 < 3 – связь между случайными величинами x и y мало вероятна.

b) составим уравнение прямых линий регрессии X на Y и Y на X.

=

= = = 10 , = = = 7,75

- 10 = 0,4 ** (y - 7,75)

= 5,78y – 44,78 + 10

= 5,78y – 34,78 – уравнение прямой линии регрессии X на Y

=

– 7,75 = 0,4 ** (х - 10)

= 0,03y – 0,28 +7,75

= 0,38y + 7,47 - уравнение прямой линии регрессии Y на X

16