Транспортная задача и задача об использовании сырья






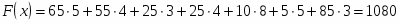
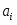
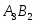

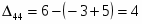


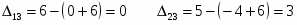
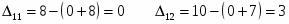
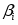
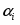
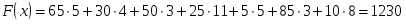
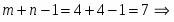
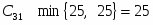
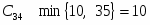
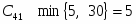
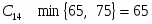
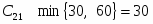
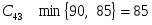
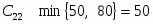
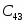
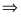
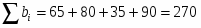
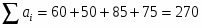
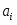
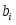
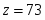
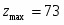
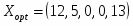
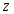

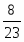
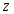

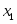
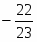

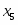
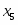
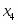
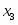
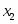
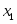
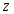
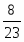
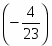
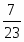
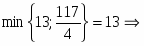
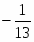
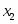
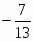
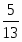
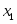
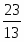
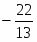
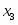
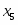
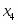
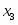
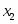
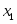
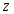
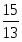
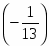
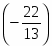
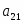
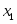
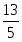
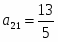
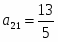
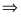
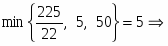
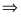
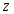
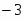
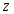
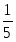
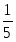
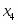
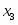
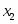
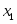
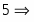
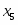
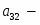
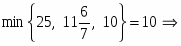
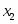
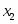
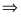
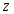
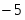
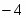
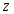
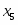
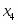
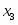
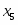
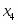
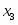
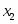
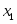
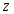
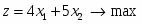
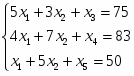
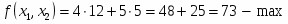
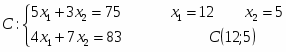
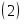
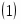

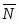
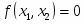
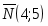
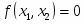
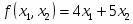
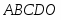
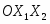
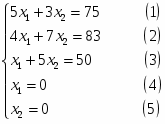
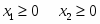
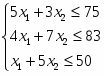
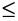
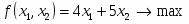
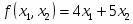
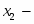
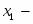
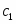
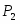
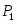

Транспортная задача и задача об использовании сырья
1. Решить задачу об использовании сырья геометрическим способом и симплекс методом, дать экономическую интерпретацию.
75
5
3
83
4
7
50
1
5
4
5
Геометрический способ.
Пусть количество выпускаемой продукции первого вида, тогда количество выпускаемой продукции второго вида. Прибыль от реализации всей продукции составляет .
Цель задачи (максимализация прибыли) запишется в виде
Расход ресурса
Запас ресурса
Структура всех трёх ограничений одинакова
Перейдём из неравенств к уравнениям
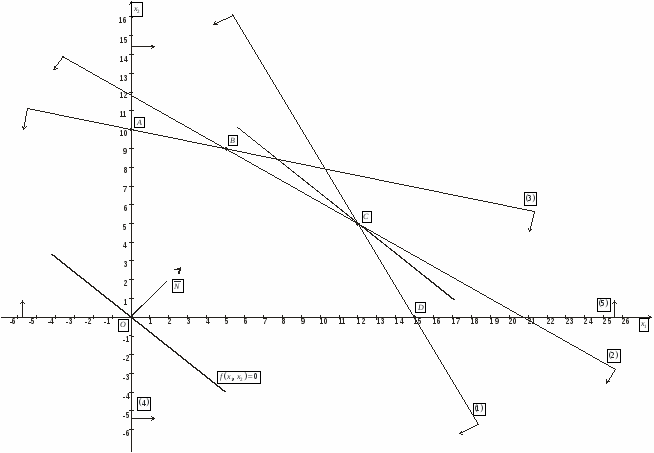
Построим прямые на плоскости
Многоугольник решений . Для нахождения максимума функции построим начальную прямую и вектор . Передвигая прямую вдоль вектора получим, что максимальное значение наша прямая принимает в точке точке пересечения прямых и .
.
Симплекс метод.
Приведём систему неравенств к системе уравнений
Целевая функция – функция прибыли
Составим симплекс таблицу:
- Первое ограничение запишем в первую строку
- Второе ограничение запишем во вторую строку
- Третье ограничение запишем в третью строку
Целевую функцию запишем в строку
Б
З
75
5
3
1
0
0
83
4
7
0
1
0
50
1
5
0
0
1
0
0
0
0
В строке есть отрицательные начальный план не оптимален. Найдём наименьший отрицательный элемент строки . Переменная будет включена в базис. Столбец переменной – ведущий. Подсчитаем симплексные отношения и найдём среди них минимальное третья строка ведущая, а элемент разрешающий. Следовательно переменная выйдет из базиса.
Проведём одну интеракцию метода замещения Жордано-Гаусса. Столбцы. Разрешающий элемент
равен поделим третью строку на 5, столбец сделаем единичным для этого третью строку умножим на и прибавим к первой строке, третью строку умножим на и сложим со второй строкой; третью строку сложим со строкой . Получим новую симплексную таблицу
Б
З
45
0
1
0
13
0
0
1
10
1
0
0
50
0
0
0
1
В строке есть отрицательные план не оптимальный. Рассчитаем симплексные отношения и найдём среди них минимальное вторая строка ведущая разрешающий
Следовательно, переменная выйдёт из базиса. Так как разрешающий элемент , поделим строку, соответствующую переменной на . Элементы столбца, соответствующего переменной отличны от элемента сделаем нулевыми, для этого вторую строку умножим на и прибавим к первой; вторую строку умножим на и прибавим к третьей; вторую строку умножим на и прибавим к строке . Получим новую симплексную таблицу
Б
З
23
0
0
1
5
1
0
0
9
0
1
0
65
0
0
0
В строке есть отрицательный элемент – пересчитываем таблицу. Рассчитываем симплексные отношения и найдём среди них минимальные первая строка ведущая разрешающий элемент переменная выйдет из базиса. Сделаем элемент единичным, для этого поделим первую строку на . Столбец, соответствующий переменной сделаем единичным для этого первую строку умножим на и прибавим ко второй строке. Первую строку умножим на и прибавим к третьей. Первую строку умножим на и прибавим к строке . Получим новую симплексную таблицу.
Б
З
13
0
0
1
12
1
0
0
5
0
1
0
73
0
0
0
Так как в строке все элементы неотрицательны, то найден оптимальный план
Оптимальный план найденный геометрическим способом и симплексным методом совпадают. Предприятию необходимо выпускать 12 единиц продукции первого вида и 5 единиц продукции второго вида. В этом случае предприятие получит прибыль денежных единиц.
2. Решить транспортную задачу распределительным методом, оценивая свободные клетки по методу потенциалов.
60
50
85
75
65
8
10
6
5
65
80
4
30
3
50
5
9
35
11
25
4
4
8
10
90
5
5
5
3
85
6
Проверим необходимое и достаточное условие разрешимости задачи
Потребность в грузе равна запасам груза задача закрытая, следовательно, имеет единственное решение.
Используя метод наименьшей стоимости заполним таблицу.
Среди тарифов наилучшим является и . Направим например,
в клетку
в клетку
в клетку
в клетку
в клетку
в клетку
в клетку
Запасы поставщиков исчерпаны, запросы потребителей удовлетворены полностью. В результате получили первый опорный план. Подсчитаем число занятых клеток таблицы их 7, а должно быть опорный план не вырожденный.
Определим значение целевой функции первого опорного плана
Проверим оптимальность плана.
Найдём потенциалы и по занятым клеткам таблицы
Пусть , тогда:
Подсчитаем оценки свободных клеток
Первый опорный план не является оптимальным так как .
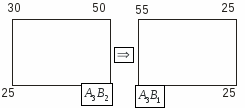
Переходим к его улучшению. Для клетки строим цикл перераспределения
В результате получили новый опорный план
60
50
85
75
65
8
10
6
5
65
80
4
55
3
25
5
9
35
11
4
25
4
8
10
90
5
5
5
3
85
6
Определим значение целевой функции
Проверим оптимальность плана
Подсчитаем оценки свободных клеток
План близок к оптимальному.
При дальнейшем перераспределении груза, задача входит в циклическую фазу, план не улучшается. Таким образом, полученное решение является наиболее оптимальным для нашей задачи

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ