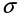
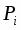
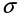
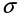
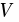
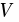
Содержание

1)Поверхностный интеграл второго рода

2)Вычисление интеграла по поверхности

3)Теорема Остроградского-Гаусса

4)Дивергенция

Литература

интеграл теорема доказательство

Интеграл по поверхности

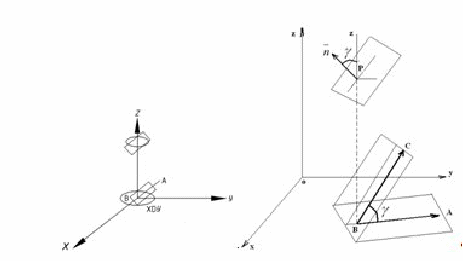
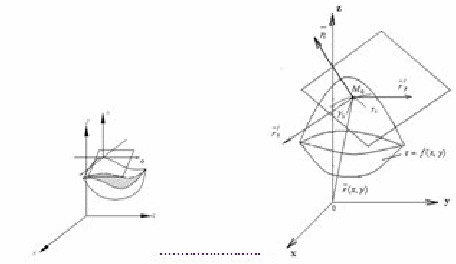
Поверхность будем рассматривать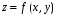

1. как образ замкнутой области при непрерывном отображении

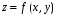
2. Отображение можно задать в векторном виде 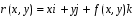в каждой точке гладкой поверхности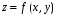

3. Для 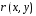существует нормаль 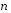, перпендикулярный к касательным 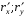кривым 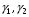в точке 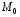. Следовательно 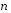равен векторному произведению касательных к 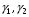векторов:

,

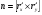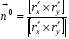
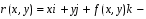
поверхность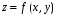

-

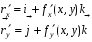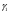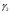направление касательных прямых к и в т.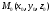 к поверхности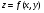

.

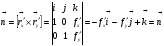
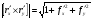
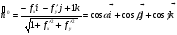Направляющие косинусы нормали 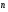к поверхности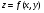

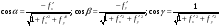
Задание векторного поля характеризует задание вектор функции:

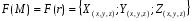
Примеры векторных полей:

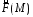- поле скоростей текущей жидкости или газа.

- гравитационное поле

- электростатистическое поле.

Если в какой то области , заполненной жидкостью (или газом), текущей с некоторой скоростью 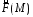, к каждой точке 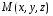можно поставить в соответствие векторное поле 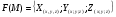, то получим векторное поле скоростей текущей жидкости.

Поверхностный интеграл второго рода.

Определение интеграла по поверхности.

Вычисление.

Дано: - область ограниченная поверхностью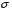

Дано: - поверхность

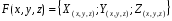
-векторное поле скоростей текущей жидкости или газа через поверхность 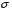в направлении нормали .

Функции 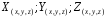- непрерывны в области с границей .

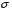Т/н : поток жидкости (или газа) через поверхность в направлении .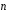

Решение.

1. Поверхность разобьем на 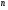произвольных частей.

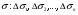
2. Выберем по точке

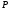
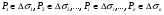
3. Вычислим 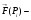скорость течения жидкости в точке

4. Определим 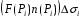, где 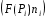-скалярное произведение

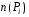-единичная нормаль к поверхности в точке

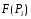- вектор в точке .

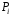5. Составим

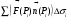
6. Найдем

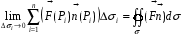
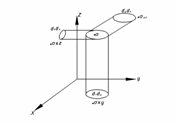
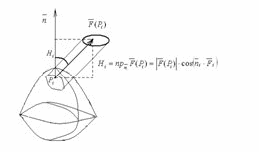
Механический смысл интеграла по поверхности

-

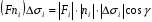
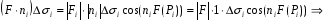
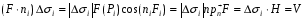объем цилиндра с основанием 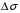и высотой .

Если -скорость течения жидкости , то 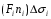равно количеству жидкости или газа протекающий через поверхность 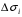за единицу времени в направлении нормали .

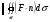- общее количество жидкости или газа протекающей через поверхность 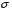в положительном направлении нормали равен потоку векторного поля 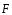через поверхность 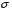в направлении нормали .

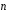Вычисление интеграла по поверхности

Пусть нормаль :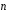

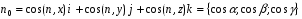
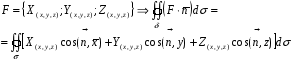
Заметим, что

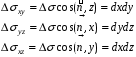
Действительно, 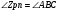как углы со взаимно перпендикулярными сторонами. Следовательно 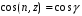, 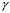-угол между касательной плоскостью к 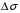и его проекцией на плоскость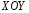

Следовательно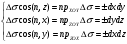

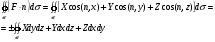
Вычисление интеграла по поверхности.

1.

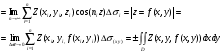
Аналогично

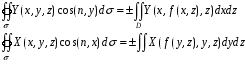
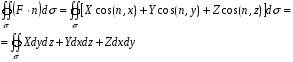
Пример 1.

Найти поток вектора 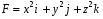через часть поверхности параболоида

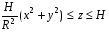в направлении внутренней нормали.

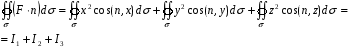
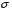-проектируется на 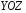с двух сторон и 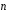образует с осью Ох углы 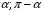(острый и тупой )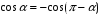

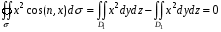
Аналогично

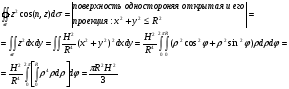
Пример 2. Вычислить 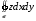, где 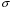-сфера 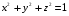, нормаль 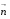внешняя.

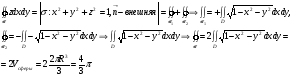
Пример 3. Найти поток вектора 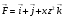через часть сферы 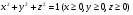в направлении внешней нормали

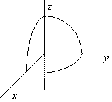
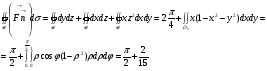
Пример 4.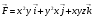

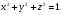
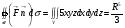
Пример 5.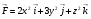

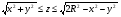
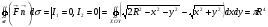
Теорема Остроградского-Гаусса.

Дивергенция.

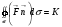
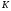-поток вектора через поверхность 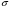в направлении за единицу времени есть разность между количеством жидкости вытекающей из области 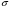и количеством жидкости втекающей в область .

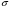1. 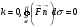. Следовательно из области 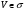жидкости вытекает столько же сколько втекает.

2. 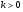жидкости или газа вытекает больше, внутри 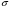существует источник.

3. 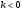жидкости или газа втекает больше чем вытекает , внутри 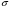существует сток.

Чтобы оценить мощность источников и стоков внутри 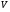нам необходима теорема Остроградского-Гаусса.

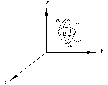
Если 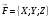-непрерывна вместе с частными производными в области 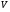то:

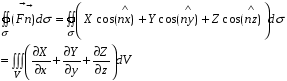
Поток изнутри 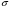равен суммарной мощности источников и стоков в области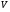

за единицу времени.

Величина потока вектора через замкнутую поверхность :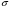

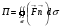является глобальной характеристикой векторного поля в области 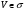и очень приблизительно позволяет судить о наличии источников и стоков в области .

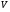• Поток представляет собой избыток жидкости протекающей в сторону положительной нормали , а не абсолютное количество жидкости прошедшей через 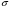независимо от направления течения. В связи с этим удобно ввести локальную характеристику распределения стоков и источников. Такой характеристикой является дивергенция (плотность потока в точке):

Дивергенция:

Определение: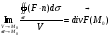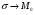- 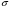стягивается в точку.

Определение: Дивергенцией векторного поля 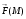в точке 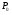называется предел отношения потока векторного поля через поверхность 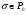к объему 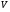, ограниченному этой поверхностью, при условии что поверхность 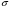стягивается в точке .

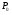Дивергенция характеризует отнесенную к единице объема мощность потока векторного поля 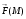исходящего из точки 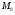, т.е. мощность источника и стока 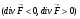находящегося в точке .

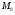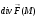- средняя объемная мощность потока .

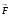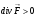-существует источник в точке .

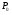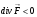- существует сток в точке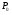

Теорема 2.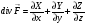

Доказательство: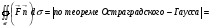

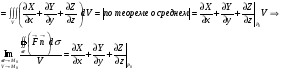
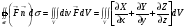ч.т.д.

Пример 1. 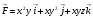. Найти поток вектора 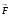через всю поверхность тела 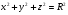, в направлении внешней нормали.

Решение:

1.

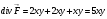
2.

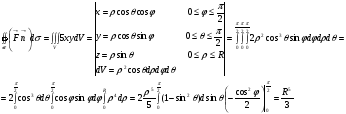
Литература

1. Ефимов А.В. Математический анализ (специальные разделы). – М. Высшая школа, 1980

2. Ильин В.А., Садовничий В.А., Сендов Б.Х. Математический анализ, I,II ч. М. Издательство МГУ, 1987

3. Шилов Г.Е. Математический анализ функции нескольких вещественных переменных. ч. 1 – 2, М., Наука. Главная редакция физико-математической литературы, 1972.

4. Сборник задач по математике для втузов. Специальные разделы математического анализа I,II ч. М. Наука 1981.