Временные ряды в эконометрических исследованиях
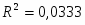
Федеральное агентство по образованию российской федерации
Новгородский государственный университет имени Ярослава Мудрого
Институт экономики и управления
Кафедра СЭММ
ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №4
ВРЕМЕННЫЕ РЯДЫ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ
Вариант №16
Выполнил:
Студент группы 8431
Яросвет И.В.
Проверил:
Орлов А.С.
ВЕЛИКИЙ НОВГОРОД 2010
Задание 4:
Проанализировать автокорреляцию уровней временного ряда, выявить и охарактеризовать его структуру.
Построить аддитивную и мультипликативную модель временного ряда, характеризующую зависимость уровней ряда от времени.
На основе лучшей модели сделать прогноз на следующие два квартала с учетом выявленной сезонности.
Таблица 1
Данные о предприятии
№ наблюдения
год
квартал
Стоимость ОПФ на конец квартала, млн.руб.
6
2001
2
898
7
2001
3
794
8
2001
4
1441
9
2002
1
1600
10
2002
2
967
11
2002
3
1246
12
2002
4
1458
13
2003
1
1412
14
2003
2
891
15
2003
3
1061
16
2003
4
1287
17
2004
1
1635
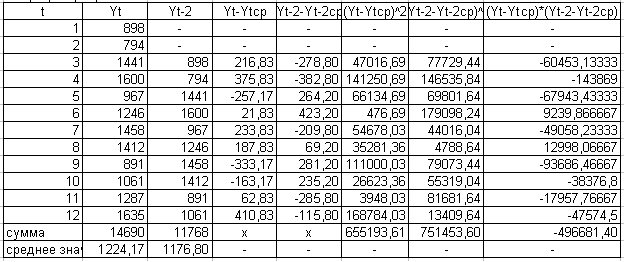
Таблица 2
Вспомогательные расчеты по определению коэффициента автокорреляции первого порядка
Таким образом,
 ,
,
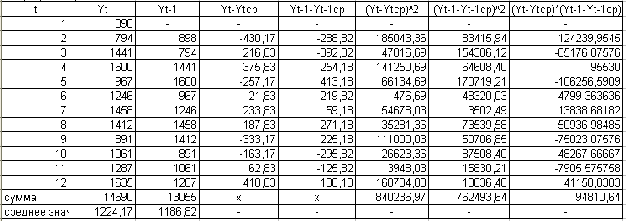
Таблица 3
Вспомогательные расчеты по определению коэффициента автокорреляции второго порядка
Таким образом,
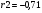 ,
,
Таблица 4
Вспомогательные расчеты по определению коэффициента автокорреляции третьего порядка
t
Yt
Yt-3
Yt-Ytср
Yt-3-Yt-3ср
(Yt-Ytср) 2
(Yt-3-Yt-3ср) 2
(Yt-Ytср)*(Yt-3-Yt-3ср)
1
898
-
-
-
-
-
-
2
794
-
-
-
-
-
-
3
1441
-
-
-
-
-
-
4
1600
898
375,83
-291,67
141250,69
85069,44
-109618,0556
5
967
794
-257,17
-395,67
66134,69
156552,11
101752,2778
6
1246
1441
21,83
251,33
476,69
63168,44
5487,444444
7
1458
1600
233,83
410,33
54678,03
168373,44
95949,61111
8
1412
967
187,83
-222,67
35281,36
49580,44
-41824,22222
9
891
1246
-333,17
56,33
111000,03
3173,44
-18768,38889
10
1061
1458
-163,17
268,33
26623,36
72002,78
-43783,05556
11
1287
1412
62,83
222,33
3948,03
49432,11
13969,94444
12
1635
891
410,83
-298,67
168784,03
89201,78
-122702,2222
сумма
14690
10707
x
x
608176,92
736554,00
-119536,67
среднее знач.
1224,17
1189,67
-
-
-
-
-
Таким образом, r3=-0.18,
Таблица 5
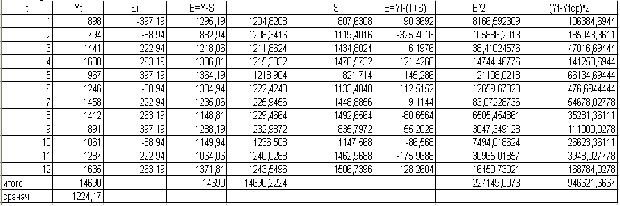
Вспомогательные расчеты по определению коэффициента автокорреляции четвертого порядка
t
Yt
Yt-4
Yt-Ytср
Yt-4-Yt-4ср
(Yt-Ytср)^2
(Yt-4-Yt-4ср)^2
(Yt-Ytср)*(Yt-4-Yt-4ср)
1
898
-
-
-
-
-
-
2
794
-
-
-
-
-
-
3
1441
-
-
-
-
-
-
4
1600
-
-
-
-
-
-
5
967
898
-257,17
-329,00
66134,69
108241,00
84607,83333
6
1246
794
21,83
-433,00
476,69
187489,00
-9453,833333
7
1458
1441
233,83
214,00
54678,03
45796,00
50040,33333
8
1412
1600
187,83
373,00
35281,36
139129,00
70061,83333
9
891
967
-333,17
-260,00
111000,03
67600,00
86623,33333
10
1061
1246
-163,17
19,00
26623,36
361,00
-3100,166667
11
1287
1458
62,83
231,00
3948,03
53361,00
14514,5
12
1635
1412
410,83
185,00
168784,03
34225,00
76004,16667
сумма
14690
9816
x
x
466926,22
636202,00
369298,00
среднее знач.
1224,17
1227,00
-
-
-
-
-
Таким образом, r4=0,68,
Таблица 6
Автокорреляционная функция и коррелограмма временного ряда объема выпуска товара фирмой
лаг
коэфавтокорреляции
коррелограмма
1
0,12
*
2
-0,71
*******
3
-0,18
**
4
0,68
*******
Построение аддитивной модели временного ряда с сезонными колебаниями.
Таблица 7
Расчет оценок сезонной компоненты в аддитивной модели
t
Yt
итого за 4 квартала
скольз.сред.
центрсколсред
оценка сезонной компоненты
1
898
-
-
-
-
2
794
4733
1183,25
-
-
3
1441
4802
1200,5
1191,875
249,125
4
1600
5254
1313,5
1257
343
5
967
5271
1317,75
1315,625
-348,625
6
1246
5083
1270,75
1294,25
-48,25
7
1458
5007
1251,75
1261,25
196,75
8
1412
4822
1205,5
1228,625
183,375
9
891
4651
1162,75
1184,125
-293,125
10
1061
4874
1218,5
1190,625
-129,625
11
1287
-
-
-
-
12
1635
-
-
-
-
Таблица 8
Расчет значений сезонной компоненты в аддитивной модели
показатели
год
1 кв
2 кв
3 кв
4 кв
1
-
-
249,125
343
2
-348,625
-48,25
196,75
183,375
3
-293,125
-129,625
-
-
итого за i кв
-641,75
-177,875
445,875
526,375
средняя оценка сезонной компоненты для i квартала, Sср
-320,875
-88,9375
222,9375
263,1875
скорректированная сезонная компонента, Si
-397,19
-88,94
222,94
263,19
Для данной модели имеем:
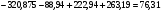
Определим корректирующий коэффициент:
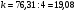
Проверим условие равенства нулю суммы значений сезонной компоненты:
-397,19-88,94+222,94+263,19=0
Таблица 9
Расчет выровненных значений T и ошибок E в аддитивной модели
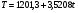 ,
,
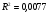
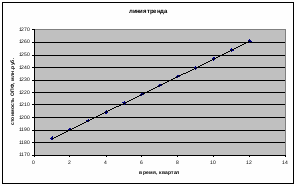
Рисунок 1 – стоимость ОПФ, млн. руб. (фактические, выровненные и полученные по аддитивной модели значения уровней ряда)
Для оценки качества построенной модели или для выбора наилучшей модели используется ошибка е.
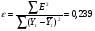
Следовательно, можно сказать, что аддитивная модель объясняет 76,1% общей вариации временного ряда.
Построение мультипликативной модели временного ряда
Таблица 10
Расчет оценок сезонной компоненты в мультипликативной модели
t
Yt
итого за 4 квартала
скольз. сред.
Центр скол. сред
оценка сезонной компоненты
1
898
-
-
-
-
2
794
4733
1183,25
-
-
3
1441
4802
1200,5
1191,875
1,21
4
1600
5254
1313,5
1257
1,27
5
967
5271
1317,75
1315,625
0,74
6
1246
5083
1270,75
1294,25
0,96
7
1458
5007
1251,75
1261,25
1,16
8
1412
4822
1205,5
1228,625
1,15
9
891
4651
1162,75
1184,125
0,75
10
1061
4874
1218,5
1190,625
0,89
11
1287
-
-
-
-
12
1635
-
-
-
-
Таблица 11
Расчет сезонной компоненты в мультипликативной модели
показатели
год
1 кв
2 кв
3 кв
4 кв
1
-
-
1,21
1,27
2
0,74
0,96
1,16
1,15
3
0,75
0,89
-
-
итого за i кв
1,49
1,85
2,37
2,42
средняя оценка сезонной компоненты для i квартала, Sср
0,745
0,925
1,185
1,21
скорректированная сезонная компанента, Si
0,73
0,91
1,17
1,19
Имеем:
0,745+0,925+1,185+1,21=4,07
Определим корректирующий коэффициент: 
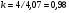 .
.
Проверим условие равенства 4 суммы значений сезонной компоненты:
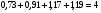
Таблица 12
Расчет выровненных значений Ф и ошибок Е в мультипликативной модели
t
Yt
Si
T*E=Y/S
T
T*S
E=Yt/(T*S)
E^2
(Yt-T*S)^2
1
898
0,73
1230,137
1183,465
863,9295
1,039437
1,0804287
1160,802377
2
794
0,91
872,5275
1190,5
1083,355
0,732908
0,5371548
83726,31603
3
1441
1,17
1231,624
1197,535
1401,116
1,028466
1,0577421
1590,737444
4
1600
1,19
1344,538
1204,57
1433,438
1,116197
1,2458965
27742,79991
5
967
0,73
1324,658
1211,605
884,4717
1,093308
1,1953226
6810,928554
6
1246
0,91
1369,231
1218,64
1108,962
1,123573
1,2624159
18779,30381
7
1458
1,17
1246,154
1225,675
1434,04
1,016708
1,0336956
574,0935801
8
1412
1,19
1186,555
1232,71
1466,925
0,962558
0,9265175
3016,74464
9
891
0,73
1220,548
1239,745
905,0139
0,984515
0,9692704
196,3879918
10
1061
0,91
1165,934
1246,78
1134,57
0,935156
0,8745171
5412,515472
11
1287
1,17
1100
1253,815
1466,964
0,877322
0,7696946
32386,87933
12
1635
1,19
1373,95
1260,85
1500,412
1,089701
1,1874484
18114,06433
итого
14690
12
14665,85
14665,89
14683,2
11,99985
12,140104
199511,5735
Ср знач
1224,17
Т=7,035t+1176,43
Рисунок 2 – стоимость ОПФ, млн. руб. (фактические, выровненные и полученные по мультипликативной модели значения уровней ряда)
Следовательно, ошибка е мультипликативной модели составит:
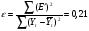
Таким образом, доля объясненной дисперсии уровней ряда в мультипликативной модели составит 79%
Прогнозирование
Для прогнозирования из двух рассмотренных моделей необходимо выбрать ту, у которой ошибка е наименьшая. Следовательно, при прогнозировании будет использоваться мультипликативная модель, так как 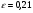
Таким образом, прогнозное значение 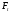 уровня временного ряда в мультипликативной модели есть сумма трендовой и сезонной компонент.
уровня временного ряда в мультипликативной модели есть сумма трендовой и сезонной компонент.
Объем товаров, выпущенного фирмой в течение первого полугодия ближайшего следующего, т. е. четвертого года, рассчитывается как сумма объемов выпущенных товаров в I и во II кварталах четвертого года, соответственно 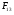 и
и 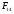 . Для определения трендовой компоненты воспользуемся уравнением тренда:
. Для определения трендовой компоненты воспользуемся уравнением тренда:
Т=7,035t+1176,43
Получим:
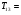 7.035*13+1176.43=1267.885
7.035*13+1176.43=1267.885
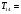 7.035*14+1176.43=1274.92
7.035*14+1176.43=1274.92
Значения сезонной компоненты равны:
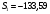 (I квартал);
(I квартал);
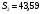 (II квартал)
(II квартал)
Таким образом,
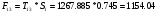 ;
;
 .
.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ