Содержание

Введение

1. Анализ технико-экономических показателей

2. Отсев несущественных показателей

3. Проверка отсутствия мультиколлинеарности

4. Расчет коэффициента автокорреляции

5. Построение модели в стандартизированном виде

6. Построение модели в натуральных единицах измерения

7. Исследование экономико-математической модели

8. Прогнозирование деятельности предприятия

Выводы и рекомендации

Список использованной литературы

Введение

По данным табл. 1 необходимо построить экономико-математическую модель влияния технико-экономических показателей работы предприятия на фондоотдачу и оценить перспективы его дальнейшего развития, для чего необходимо:

а) проанализировать показатели хозяйственной деятельности предприятия за указанный период времени; б) произвести отсев несущественных факторов, если такие есть в исходных данных; в) проверить наличие (отсутствие) мультиколлениарности и, в случае её присутствия, сделать отсев мультиколлениарных факторов; г) рассчитать коэффициент автокорреляции; д) построить экономико-математическую модель та оргументировать выбор уравнения связи; е) рассчитать коэффициенты эластичности; ж) построить эконометрическую модель в натуральных единицах измерения; з) определить значимость каждого показателя для фондоотдачи; и) спрогнозировать уровень фондоотдачи на предприятии, который ожидается в предстоящем периоде и рассчитать необходимые значения технико-экономических показателей для прогнозируемого периода. По всем пунктам задания сделать выводы с экономической точки зрения и дать конкретные рекомендации по экономической политики на предприятии для обеспечения его дальнейшего развития.

Таблица 1 Технико-экономические показатели

Период времени

(№)

Фондоотдача, грн

Стоимость активной части основных фондов, млн. грн

Среднечасовая выработка одного рабочего, грн

Простои оборудования, тыс./маш.часов

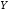
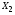
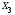
46,00

65,20

22,70

7,11

2,79

47,00

65,20

22,90

7,11

2,80

48,00

65,30

22,80

7,11

2,80

49,00

65,40

22,90

7,12

2,81

50,00

65,50

22,90

7,13

2,80

51,00

65,60

23,00

7,14

2,80

52,00

65,70

23,30

7,13

2,80

53,00

65,70

23,20

7,13

2,82

54,00

65,80

23,30

7,13

2,82

55,00

65,90

23,20

7,15

2,82

56,00

66,00

23,30

7,14

2,84

57,00

66,10

23,30

7,15

2,83

Итого:

787,40

276,80

85,55

33,73

1. Анализ технико-экономических показателей

Анализ исходных данных показал, что коэффициенты , , 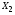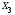возрастают, следовательно, присутствует тенденция к росту фондоотдачи.

В данной работе фондоотдача зависит от трех факторов:

– стоимость активной части основных фондов;

– среднечасовая выработка одного рабочего;

– простои оборудования.

Фондоотдача основных фондов определяется отношением объема изготовленной продукции к среднегодовой стоимости основных фондов:

,

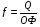где 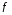– фондоотдача;

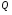– объем изготовленной продукции;

ОФ – среднегодовая стоимость основных фондов, грн.

Объем изготовленной продукции определяется в натуральных или стоимостных показателях. Чаще всего обобщающим стоимостным показателем объема производства является товарная продукция. Для сопоставления уровня и динамики фондоотдачи объем продукции вычисляют в фиксированных ценах, а объем основных фондов – по воспроизведенной стоимости, поскольку остаточная стоимость изменяется непропорционально к изменениям производственной мощности.

Фондоотдача показывает общую отдачу от использования каждой гривны, затраченную на основные производственные фонды, т.е. эффективность этого вложения средств.

2. Отсев несущественных факторов

Для отсева несущественных факторов воспользуемся формулой парной корреляции, которая имеет следующий вид:

.

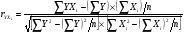Для вычисления коэффициентов парной корреляции по этой формуле численные значения параметров Y, Х₁, Х₂, Х₃ определяются путем суммирования исходных данных, приведенных в табл. 1. Для определения численных значений параметров Y², YХ₁, YХ₂, YХ₃, Х₁², Х₂², Х₃², необходимо провести дополнительные промежуточные расчеты, результаты которых представлены в табл. 2.

Таблица 2 Промежуточные расчеты показателей для отсева несущественных факторов

№

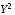
YX₁

YX₂

YX₃

X₁²

X₂²

X₃²

1

2

3

4

5

6

7

8

46

4251,040

1480,040

463,572

181,908

515,290

50,552

7,784

47

4251,040

1493,080

463,572

182,560

524,410

50,552

7,840

48

4264,090

1488,840

464,283

182,840

519,840

50,552

7,840

49

4277,160

1497,660

465,648

183,774

524,410

50,694

7,896

50

4290,250

1499,950

467,015

183,400

524,410

50,837

7,840

51

4303,360

1508,800

468,384

183,680

529,000

50,980

7,840

52

4316,490

1530,810

468,441

183,960

542,890

50,837

7,840

53

4316,490

1524,240

468,441

185,274

538,240

50,837

7,952

54

4329,640

1533,140

469,154

185,556

542,890

50,837

7,952

55

4342,810

1528,880

471,185

185,838

538,240

51,123

7,952

56

4356,000

1537,800

471,240

187,440

542,890

50,980

8,066

57

4369,210

1540,130

472,615

187,063

542,890

51,123

8,009



51667,580

18163,370

5613,550

2213,293

6385,400

609,903

94,812

;

;

.

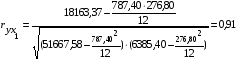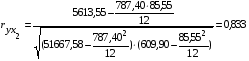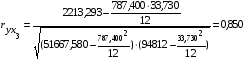Проанализируем полученные результаты. Как известно, коэффициент парной корреляции изменяется от – 1 до + 1. Если названный коэффициент находится в пределах  0,7 – 0,9, то, согласно шкале оценки взаимосвязи переменных, связь между факторами считается высокой, а если значение коэффициента превышает  0,9, то связь считается очень высокой.

В нашем случае взаимосвязь между фондоотдачей и стоимостью активной части основных фондов высокая (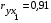). Этот фактор (Х₁) считаем существенным и включаем в модель. Взаимосвязь между фондоотдачей и среднечасовой выработкой одного рабочего высокая (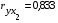). Фактор (Х₂) считаем существенным и включаем в модель. Взаимосвязь между фондоотдачей и простоем оборудования высокая (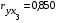). Фактор (Х₃) считаем существенным и включаем в модель.

3. Проверка отсутствия мультиколлинеарности

Для проверки отсутствия мультиколлинеарности между оставшимися факторами воспользуемся формулой парной корреляции, которая имеет следующий вид:

.

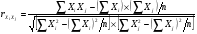Для вычисления коэффициентов парной корреляции по этой формуле необходимые численные значения параметров Y, Х₁, Х₂, Х₃ представлены в табл. 1. Численные значения параметров Х₁², Х₂², Х₃² представлены в табл. 2. Для определения численных значений параметров Х₁Х₂, Х₁Х₃, Х₂Х₃ необходимо провести дополнительные промежуточные расчеты, результаты которых представлены в табл. 3.

Таблица 3 Промежуточные расчеты показателей для проверки отсутствия мультиколлинеарности

№

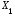
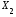
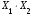
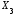
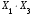
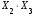
46

22,700

7,110

161,397

2,790

63,333

19,8369

47

22,900

7,110

162,819

2,800

64,120

19,908

48

22,800

7,110

162,108

2,800

63,840

19,908

49

22,900

7,120

163,048

2,810

64,349

20,0072

50

22,900

7,130

163,277

2,800

64,120

19,964

51

23,000

7,140

164,22

2,800

64,400

19,992

52

23,300

7,130

166,129

2,800

65,240

19,964

53

23,200

7,130

165,416

2,820

65,424

20,1066

54

23,300

7,130

166,129

2,820

65,706

20,1066

55

23,200

7,150

165,88

2,820

65,424

20,163

56

23,300

7,140

166,362

2,840

66,172

20,2776

57

23,300

7,150

166,595

2,830

65,939

20,2345



276,800

85,550

1973,38

33,730

778,067

240,4684

;

;

.

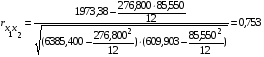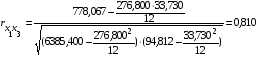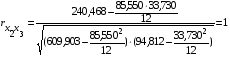В данном случае все численные значения коэффициентов парной корреляции (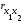,,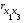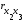) < 0.9, следовательно, мультиколлинеарность отсутствует, т.е. все коэффициенты мы оставляем и включаем в модель.

4. Расчет коэффициента автокорреляции

Для расчета коэффициента автокорреляции между уровнями валового дохода воспользуемся формулой парной корреляции, которая имеет следующий вид:

.

Для вычисления коэффициента автокорреляции по этой формуле необходимые численные значения параметров Y_i, Y_i², представленные в табл. 1 и 2 соответственно. Для определения численных значений параметров Y_i-1, Y_i-1², Y_iY_i-1 необходимо провести дополнительные промежуточные расчеты, результаты которых представлены в табл. 4.

Кроме того, для расчета коэффициента автокорреляции необходимо предварительно вычислить средние значения параметров 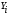и 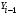, а также квадраты средних значений этих же параметров, для чего воспользуемся формулами средней арифметической простой:

Таблица 4 Промежуточные расчеты показателей для расчета коэффициента автокорреляции

№

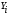
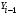
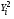
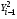
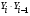
46

65,200

4251,040

47

65,200

65,200

4251,040

4251,040

4251,040

48

65,300

65,200

4264,090

4251,040

4257,560

49

65,400

65,300

4277,160

4264,090

4270,620

50

65,500

65,400

4290,250

4277,160

4283,700

51

65,600

65,500

4303,360

4290,250

4296,800

52

65,700

65,600

4316,490

4303,360

4309,920

53

65,700

65,700

4316,490

4316,490

4316,490

54

65,800

65,700

4329,640

4316,490

4323,060

55

65,900

65,800

4342,810

4329,640

4336,220

56

66,000

65,900

4356,000

4342,810

4349,400

57

66,100

66,000

4369,210

4356,000

4362,600



787,400

721,300

51667,580

47298,370

47357,410

;

.

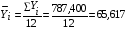
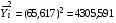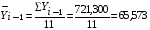
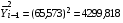
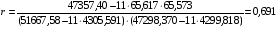Проанализируем полученный результат. Если численное значение коэффициента автокорреляции находится в диапазоне от –0,3 до + 0,3, то принято считать, что существует автокорреляция между уровнями результирующего показателя. В нашем случае коэффициент автокорреляции составляет r = 0,691, следовательно, автокорреляция между уровнями фондоотдачи отсутствует. Это свидетельствует о том, что факторы, от которых зависит фондоотдача и которые даны нам в качестве исходной информации, являются основными, а влияние случайных, нам не известных факторов незначительно. По этой причине считаем, что искажение результатов моделирования будет несущественным, поскольку в модель будут включены только существенные факторы, от которых действительно зависит результирующая переменная.

5. Построение модели в стандартизированном виде

По характеру изменения уровней фондоотдачи можно выдвинуть гипотезу о прямолинейном законе распределения этого показателя во времени. Уравнение множественной регрессии для прямолинейной связи имеет следующий вид:

.

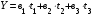Для решения этого уравнения регрессии воспользуемся методом исключения (методом Гаусса), для чего составим и запишем систему нормальных уравнений:

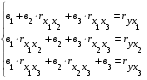
Решить систему нормальных уравнений – значит, найти численное значение коэффициентов регрессии 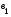, , 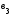. Все остальные параметры системы уравнений (коэффициенты парной корреляции) уже были вычислены на первом и втором этапах расчетов. Запишем эту же систему уравнений с численными значениями известных параметров:

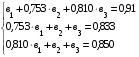
Разделим каждый член каждого уравнения системы на соответствующие коэффициенты при .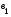

В результате этой процедуры (деления) получим новую систему уравнений с тремя неизвестными, в которой коэффициенты при 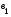, равны единице:

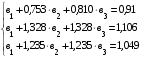
Для исключения из системы уравнений неизвестного параметра 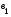вычтем из второго уравнения – первое, и из третьего уравнения – первое. В результате этой операции (вычитания) получим новую систему из двух уравнений, но уже только с двумя неизвестными:

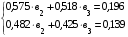
Как и в предыдущем случае, разделим каждый член каждого уравнения этой системы на соответствующие коэффициенты при .

В результате этой процедуры (деления) получим новую систему, состоящую из двух уравнений с двумя неизвестными, в которой коэффициенты при равны единице:

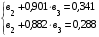
Для исключения из этой системы уравнений неизвестного параметра вычтем из второго уравнения первое. В результате этой операции (вычитания) получим новое уравнение, но уже только с одним неизвестным:

.

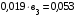Откуда

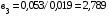
Для определения численного значения коэффициента регрессии подставим найденное значение коэффициента регрессии 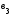в первое уравнение системы из двух уравнений:

;

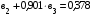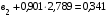
Откуда

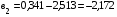
Для определения численного значения коэффициента регрессии 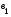подставим найденные значения коэффициентов регрессии и 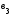в первое уравнение системы из трех уравнений:

;

;

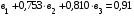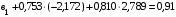Откуда

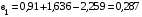
Все численные значения коэффициентов множественной регрессии найдены. Тогда уравнение связи в стандартизированном виде будет иметь следующий вид:

.

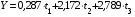6. Построение модели в натуральных единицах измерения

Для объективного анализа показателей изучаемого социально-экономического явления необходимо перейти от абстрактной стандартизированной модели к математической модели в натуральных единицах измерения. Уравнение множественной регрессии для прямолинейной связи имеет следующий вид:

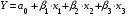
Для решения этого уравнения регрессии необходимо определить численные значения коэффициентов эластичности ₁, ₂, ₃. Для этого воспользуемся следующей формулой:

,

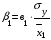где 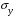– среднеквадратическое отклонение результирующего признака, которое определяется по формуле

.

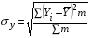Для расчета среднеквадратического отклонения и коэффициентов эластичности необходимо провести некоторые промежуточные расчеты, результаты которых представлены в табл. 5.

Таблица 5 Промежуточные расчеты для вычисления cреднеквадратического отклонения

№

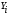
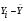
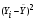
46

65,200

-0,417

0,1739

47

65,200

-0,417

0,1739

48

65,300

-0,317

0,1005

49

65,400

-0,217

0,0471

50

65,500

-0,117

0,0137

51

65,600

-0,017

0,0003

52

65,700

0,083

0,0069

53

65,700

0,083

0,0069

54

65,800

0,183

0,0335

55

65,900

0,283

0,0801

56

66,000

0,383

0,1467

57

66,100

0,483

0,2333

Итого:

787,400

1,0167

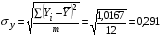
Тогда

; ; .

;

;

.

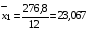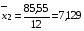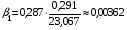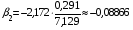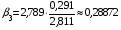В связи с тем что в формулы расчета коэффициентов эластичности входят значения 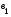, , 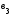с тремя десятичными знаками, а также численные значения коэффициентов эластичности малы, их следует округлить до пятого десятичного знака, чтобы модель более точно отображала результаты моделирования и прогнозирования.

Тогда уравнение множественной регрессии для прямолинейной связи для изучения фондоотдачи будет иметь следующий вид:

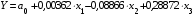
В этом уравнении регрессии его свободный член 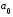является неизвестной величиной. Для определения численного значения 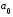необходимо в это уравнение подставить средние значения результирующей и факторных величин. Тогда уравнение примет вид:

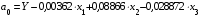
или

.

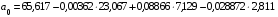
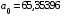Тогда экономико-математическая модель изучаемого явления в натуральных единицах измерения будет иметь следующий окончательный вид:

.

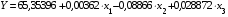Это уравнение регрессии необходимо проверить по двум критериям: по сходству сумм расчетных и экспериментальных значений фондоотдачи и по коэффициенту множественной корреляции.

Вычислим расчетные значения фондоотдачи по всем периодам времени:

;

;

;

;

;

;

;

;

;

;

;

.

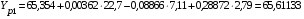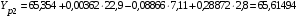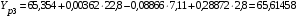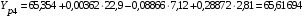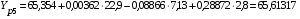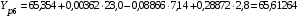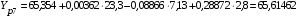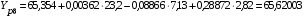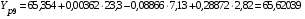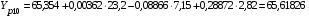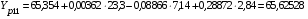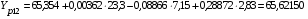Сумма всех расчетных значений фондоотдачи равна 787,40368 и совпадает с суммой эмпирических значений этого показателя, т.е. выполняется условие:

Y _эi = 787,4  Y_рi = 787,40368,

следовательно, по этому критерию можно сделать вывод о правильности построения экономико-математической модели хозяйственной деятельности предприятия.

Вычислим численное значение коэффициента множественной корреляции по формуле:

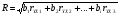
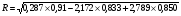= 0,91.

Так как численное значение коэффициента множественной корреляции R превышает численное значение любого из парных коэффициентов корреляции 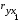, , 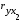, 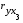а также не превышает единицы, можно сделать вывод о правильности построения экономико-математической модели хозяйственной деятельности фермерского хозяйства и по этому критерию.

Таким образом, гипотеза о прямолинейной связи между показателями рассматриваемой системы верна, и полученное уравнение множественной регрессии может использоваться в качестве модели для анализа и прогнозирования хозяйственной деятельности предприятия.

7. Исследование экономико-математической модели

Оценим степень влияния каждого фактора, включенного в эконометрическую модель, на формирование результирующей величины – уровня фондоотдачи от хозяйственной деятельности предприятия.

Для этого воспользуемся методом цепных подстановок, сущность которого заключается в последовательном, поочередном изменении численного значения каждого фактора на одну и ту же величину и в сравнении каждого последующего результата с предыдущим. Увеличим поочередно численные значения факторных переменных на 10 % и сравним полученные результаты с результатами хозяйственной деятельности в последнем (двенадцатом) временном периоде. Запишем уравнение расчетного определения фондоотдачи:

.

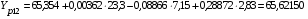Увеличим каждый факторный признак поочередно на 10 %:

;

;

.

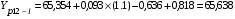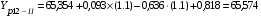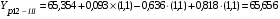Сравним каждый последующий результат с предыдущим:

;

;

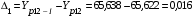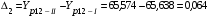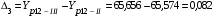
Результаты этих исследований показывают, что в данном случае существенное влияние на фондоотдачу оказывают простои оборудования (0,082 тыс.грн.). Менее влияет на фондоотдачу стоимость активной части основных фондов (0,016 тыс. грн), что касается среднечасовой выработки одного рабочего, то она оказывает негативное влияние. Исследования позволяют сделать следующие выводы о значимости каждого фактора в формировании деятельности предприятия. Факторы оказывают положительное влияние на формирование фондоотдачи предприятия (об этом свидетельствует знак «+» перед фактором).

8. Прогнозирование деятельности предприятия

Для прогнозирования экономической деятельности предприятия и разработки прогнозных показателей воспользуемся расчетно-графическим методом. Для этого необходимо графически изобразить эмпирическую регрессию показателей фондоотдачи и на этом же графике – теоретическую регрессию того же параметра. Графическое изображение фактических и расчетных значений фондоотдачи по периодам представлено на рис. 1.

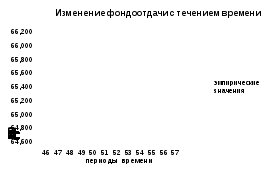
Рис. 1. Изменение фондоотдачи предприятия с течением времени:

Как следует из графика эмпирической регрессии, фондоотдача изучаемого предприятия постоянно возрастает на протяжении всего временного периода, практически стабильно, лишь в некоторые периоды времени уровни фондоотдачи оставались неизменными. Это обстоятельство необходимо учитывать при разработке прогнозных показателей деятельности предприятия.

Теоретическая регрессия показывает, что расчетные значения фондоотдачи находятся примерно на одном и том же уровне на протяжении всего рассматриваемого временного периода. При этом, как следует из графика, расчетные значения фондоотдачи не подвержены колебаниям. Следовательно, если эти расчетные данные, т.е. данные, полученные на основе созданной экономико-математической модели, использовать для разработки прогнозных показателей деятельности предприятия, то такой прогноз будет обладать высокой надежностью.

Прогнозным периодом считается тринадцатый, то есть период, который следует за последним периодом, по которому имеется исходная информация.

Для определения прогнозного уровня фондоотдачи в тринадцатом периоде продлим график расчетных значений этого показателя, и на участке, соразмерном в масштабе с тринадцатым периодом, отметим точку, соответствующую уровню фондоотдачи в этом периоде. Затем опустим перпендикуляр на ось абсцисс и определим численное значение этого показателя в прогнозном периоде. Таким образом, графически мы определили, что уровень фондоотдачи в прогнозном периоде должен составить 65,627тыс. грн.

Зная прогнозное значение фондоотдачи в тринадцатом периоде, можно вычислить численное значение первого фактора для этого же периода, поскольку, как уже отмечалось, с помощью этого фактора будет обеспечиваться прогнозный уровень в прогнозном периоде.

Запишем уравнение связи для тринадцатого периода:

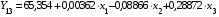
Подставив в это уравнение численное значение фондоотдачи в тринадцатом периоде и численные значения факторов х₂ и х₃ в двенадцатом периоде (предполагаем, что эти факторы не изменятся в тринадцатом периоде), определим численное значение фактора х₁, который должен измениться в тринадцатом периоде, для того чтобы обеспечить прогнозный уровень фондоотдачи:

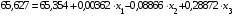
Откуда

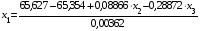
или

.

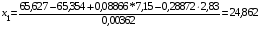Таким образом, для того чтобы обеспечить увеличение фондоотдачи в тринадцатом периоде до прогнозируемого уровня (65,627 тыс. грн.), необходимо увеличить стоимость активной части основных фондов в этом же периоде на 24,862 – 23,3 = 1,562 млн.грн по сравнению с двенадцатым периодом.

Выводы и рекомендации

Проведенный анализ технико-экономических показателей работы предприятия позволяет сделать вывод о том, что оно работает стабильно и постепенно развивается, хотя и невысокими темпами. Дальнейший рост фондоотдачи предприятия может быть обеспечен несколькими путями: увеличение среднечасовой выработки одного рабочего, стоимости активной части основных фондов, уменьшение простоев оборудования. Другими словами систематический рост фондоотдачи обеспечивается за счет увеличения производительности машин, механизмов и оборудования, сокращения их простоев, оптимальной загрузки техники, технического совершенствования производственных основных фондов. В частности, повышение производительности труда осуществляется за счет снижения трудоемкости, то есть путем механизации и автоматизации труда, внедрения новой техники и технологии. Между трудоемкостью продукции и среднечасовой выработкой существует обратно пропорциональная зависимость. Зная, как изменилась среднечасовая выработка, можно определить изменение трудоемкости продукции.

Улучшение использования основных фондов решает широкий круг экономических проблем, направленных на повышение эффективности производства: увеличение объема выпуска продукции, рост производительности труда, снижение себестоимости, экономию капитальных вложений, увеличение прибыли и рентабельности капитала и, в конечном счете, повышения уровня жизни общества.

Список использованной литературы

1. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2006. – 311 с.

2. Луговская Л.В. Эконометрика в вопросах и ответах: учебное пособие. – М.: ТК Велби, изд-во Проспект, 2005. – 208 с.

3. Лугінін О.Е., Білоусова С.В., Білоусов О.М. Економетрія: Навчальний по-сібник. – Київ: Центр навчальної літератури, 2005. – 252 с.

4. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: Учебник. – 4-е изд. – М.: Дело, 2000. – 400 с.

5. Эконометрика: Учебник для вузов / А.И. Орлов. – 3-е изд., перераб. и доп. – М.: Издательство «Экзамен», 2004. – 576 с. (Серия «Учебник для вузов»).

6. Толбатов Ю.А. Економетрика: Підручник для студентів екон. спеціальн. ви-щих навчальних закладів. – К.: ТП Пресс, 2003. – 320 с.

7.Эконометрика: Учебник / И.И. Елисеева, С.В. Курышева, Т.В. Костеева и др.; Под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статис-тика, 2005. – 576 с.

8.Економіка підприємства: Навч. посібник / За ред. А.В. Шегди. – К.: Знання, 2005. – 431 с.