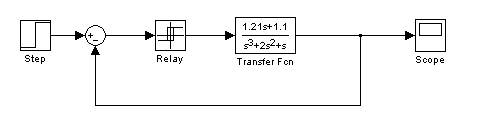
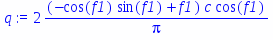
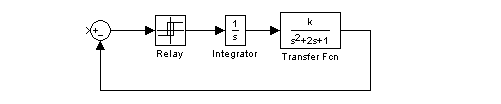
Исследовать абсолютную устойчивость нелинейной системы:

1. Определить K = Kгр, при котором система находится на границе устойчивости:

Параметры реле:

- включение x = 0.5;

- выключение x = - 0.5;

- на выходе при включении z(x) = 1;

- на выходе при выключении z(x) = -1;

z = f(x)

f(0) = 0

0 < f(x)/x < Kн

Kн = tgα = 1/0.5 =2

Нелинейная характеристика находится в 1 и 3 квадрантах, удовлетворяет выше перечисленным условиям =>

Допустимо использовать критерий В.М. Попова для исследования абсолютной устойчивости нелинейной системы.

Передаточная функция линейной части:

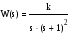
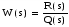
Q(s) = 0, βι < 0, полюсы левые => ЛЧ устойчива.

=>

Допустимо использовать критерий В.М. Попова для исследования абсолютной устойчивости нелинейной системы.

Передаточная функция линейной части:

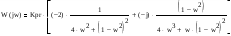
Преобразованная передаточная функция линейной части:

Wp(s) = Re(W(s)) + jwIm(W(s))

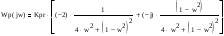
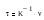
γ >0 – любое.

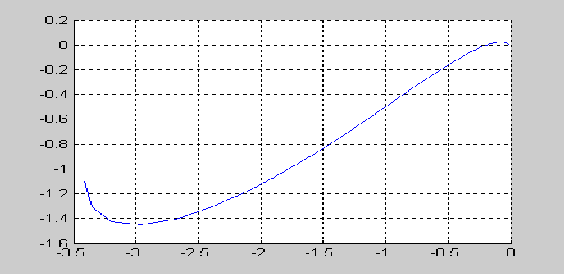
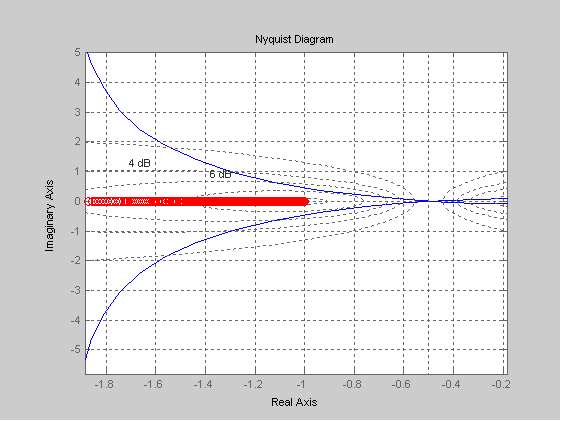
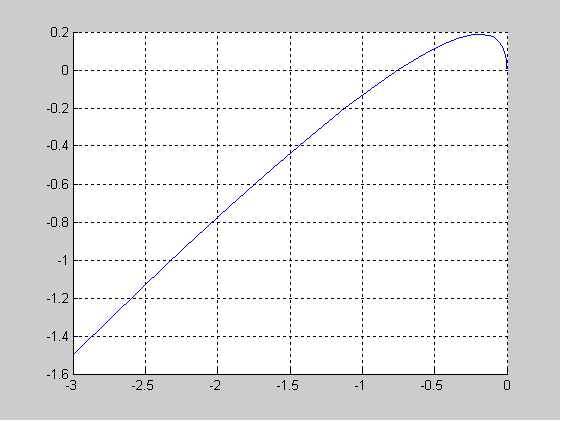
Строим годограф преобразованной ЛЧ ( в данном случае Kpr = 1.5)

Находим точку пересечения годографа преобразованной ЛЧ с мнимой осью:

Im(Wp(jw)) = 0;

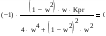
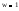
Re(W(jw))|{Im(W(jw))=0} = Kpr*(-0.5)

Kpr выбираем из условий: преобразованная частотная характеристика должна лежать справа от прямой, проведенной через точку -1/Kн на вещественной оси комплексной плоскости. Угол наклона ζ = arctg(1/τ).

(-0.5)Kpr > -1/Kн

=> Kpr < 1.

Вывод: при Kpr = 1 система находится на границе устойчивости.

2. Исследование автоколебаний (метод гарм. баланса):

Вычисляем передаточную функцию НЭ.

Wнэ(A) = q(A);

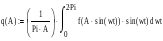
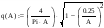
Колебания не возникнут, если отрицательный инверсный годограф НЭ не пересечет годограф ЛЧ ( Wлч = -1/q(A)).

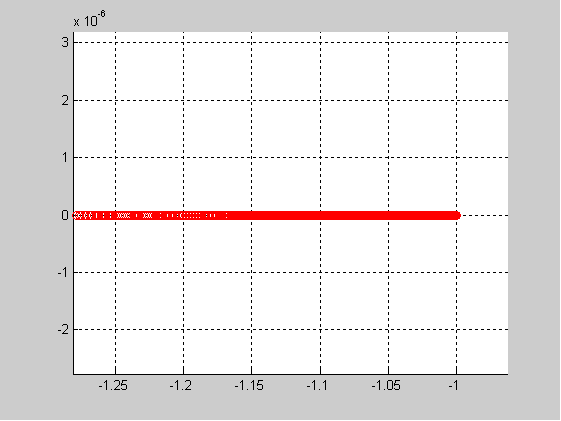
Отрицательный инверсный годограф НЭ:

Отрицательный инверсный годограф НЭ и годограф ЛЧ :

• _{Колебания не возникнут.}

_{3. При K = 1.1Kpr синтезировать корректирующее устройство:}

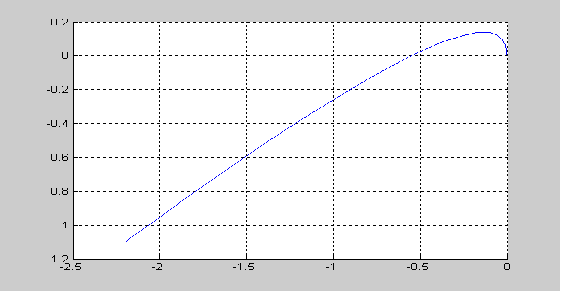
Строим годограф преобразованной ЛЧ ( в данном случае Kpr = 1.1)

Для стабилизации системы вводим дополнительное звено Wф=(T1*p +1),

T1=1/w0, T1=1/0.9=1.1

Передаточная функция скорректированной системы:

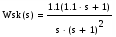
Строим годограф скорректированной преобразованной части:

Через точку -1/Kн на вещественной оси комплексной плоскости можно провести прямую(угол наклона ζ = arctg(1/τ) ), так чтобы преобразованная скорректированная частотная характеристика лежала справа от прямой.

=> Система абсолютно устойчива.

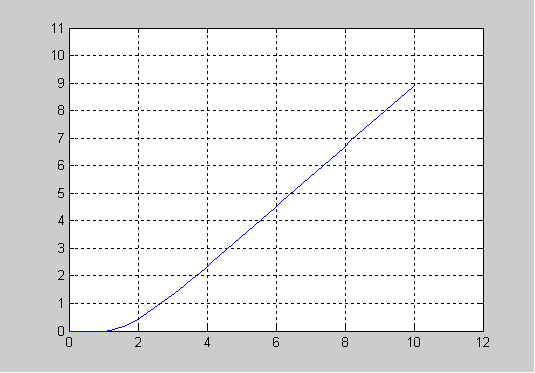
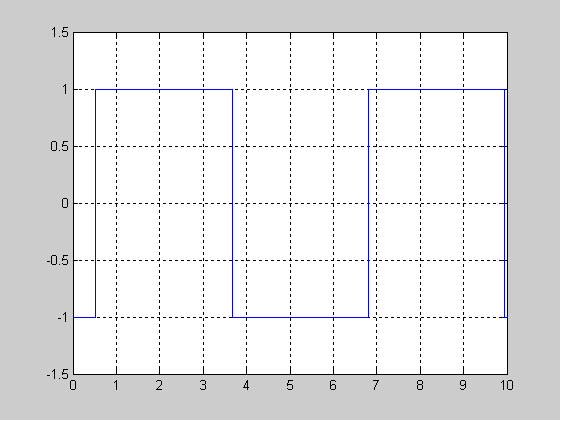
Построить переходной процесс в системе при Хвх =10:

Переходной процесс:

7