Загальні властивості однорідних лінійних диференціальних рівнянь n-го порядку
Реферат на тему:
Загальні властивості однорідних лінійних диференціальних рівнянь n-го порядку.
1. Властивості лінійного диференціального оператору.
Лінійним диференціальним рівнянням називається рівняння вигляду
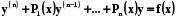 (5.1)
(5.1)
де Pi(x), i = 1,2,…, n , f(x) – задані функції, неперервні на (a,b).
1,2,…, n , f(x) – задані функції, неперервні на (a,b).
При цих умовах диференціальне рівняння (5.1) має єдиний розв’язок
y=y(x), який задовільняє початковим умовам 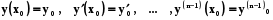 .
.
Цей розв’язок визначений і n раз неперервно диференційований на (a,b).
Особливих розв’язків диференціальне рівняння (5.1) не має. Будь-який розв’язок являється частинним. Якщо при 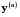 стоїть
стоїть 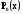 , то точки, в яких
, то точки, в яких 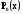 =0, називаються особливими.
=0, називаються особливими.
Якщо f(x)=0, то диференціальне рівняння (5.1) називають однорідним
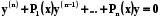 (5.2)
(5.2)
Для скорочення запису введемо лінійний диференціальний оператор
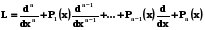 (5.3)
(5.3)
Властивості оператора L :
L (xy)=k *L (y), k = const;
L (
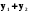 )=L (
)=L (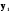 ) + L (
) + L ( );
);L
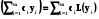 .
.
Використовуючи оператор L диференціального рівняння (5.1) і (5.2) перепишемо у вигляді L (y) = f (x) 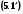 , L (y) = 0
, L (y) = 0 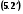 .
.
Означення 5.1. Функція y = y (x) називається розв’язком диференціального рівняння (5.1), якщо L (y)  f (x) (для диференціального рівняння (5.2)
f (x) (для диференціального рівняння (5.2)
L (y(x)) 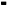 0).
0).
Лінійне диференціальне рівняння (5.1) залишається бути лінійним при будь-якій заміні незалежної змінної 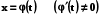 .
.
Лінійне диференціальне рівняння (5.1) залишається бути лінійним при будь-якій лінійній заміні шуканої функції 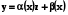 . (5.4)
. (5.4)
2. Властивості розв’язків лінійного однорідного диференціального рівняння n–го порядку.
Наша задача полягає в тому, щоб знайти всі дійсні розв’язки диференціального рівняння 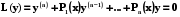 (5.5)
(5.5)
Для розв’язування такої задачі доцільно знайти деякі комплексні розв’язки.
Означення 5.2 Функцію z(x) = w(x) + iv(x), де w(x),v(x) дійсні функції, будемо називати комплексною функцією від дійсної змінної х (w(x) – дійсна частина, v(x) – уявна частина).
Приклад 5.1. Показати справедливість формул  ,
, 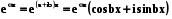 . (5.6)
. (5.6)
Формули (5.6) доводяться виходячи з розкладу відповідних множників b раз.
Похідна n-го порядку від z (x) дорівнює 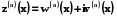 . (5.7)
. (5.7)
Приведемо формули для обчислення похідної :
а) 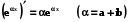 ; (5.8)
; (5.8)
Дійсно 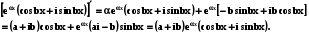
б) Для дійсного к і будь-якого 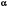 справедлива формула
справедлива формула
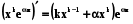 ; (5.9)
; (5.9)
в) Використовуючи (5.9) можна показати 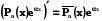 , (5.10)
, (5.10)
де 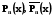 - поліноми степеня n ;
- поліноми степеня n ;
г) При будь-якому 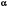 (дійсному або комплексному) справедлива формула
(дійсному або комплексному) справедлива формула
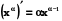 . (5.11)
. (5.11)
Формула (5.11) доводиться шляхом представлення 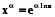 і використання формули (5.8).
і використання формули (5.8).
Означення 5.3. Комплексна функція y (x) = 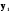 (x) + i
(x) + i (x) (5.12) називається розв’язком однорідного диференціального рівняння (5.5); якщо
(x) (5.12) називається розв’язком однорідного диференціального рівняння (5.5); якщо
L (y(x)) 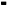 0, a < x < b .
0, a < x < b .
Комплексний розв’язок (5.12) утворює два дійсних розв’язки  (x),
(x),  (x).
(x).
Дійсно L (y(x)) = L (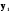 (x) + i
(x) + i (x)) = L(
(x)) = L(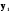 (x)) + iL(
(x)) + iL( (x)) = 0 .
(x)) = 0 .
Звідки L(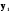 (x)) = 0, L(
(x)) = 0, L( (x)) = 0.
(x)) = 0.
Властивості розв’язків лінійного однорідного диференціального рівняння (5.5).
а) Якщо 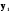 (x) – розв’язок , тобто L(
(x) – розв’язок , тобто L(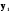 )
) 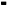 0, то y=c
0, то y=c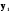 (x), де с – довільна константа , теж розв’язок диференціального рівняння (5.5)
(x), де с – довільна константа , теж розв’язок диференціального рівняння (5.5)
L(с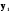 ) = сL(
) = сL(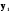 ) = 0.
) = 0.
б) Якщо  (x),
(x),  (x) - розв’язки диференціального рівняння (5.5) , то
(x) - розв’язки диференціального рівняння (5.5) , то
у=  (x)+
(x)+ (x) теж розв’язок . Дійсно L (
(x) теж розв’язок . Дійсно L ( +
+ ) = L (
) = L ( )+L (
)+L ( ) = 0.
) = 0.
в) Якщо  (x),
(x),  (x), ... ,
(x), ... , 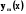 ) - розв’язки диференціального рівняння (5.5), то їх лінійна комбінація також являється розв’язком
) - розв’язки диференціального рівняння (5.5), то їх лінійна комбінація також являється розв’язком
L 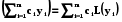 = 0.
= 0.
Приклад 5.2. Записати двохпараметричне сімейство розв’язків.
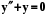 ,
, 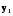 =cos(x),
=cos(x),  =sin(x) - розв’язки, тоді y = c
=sin(x) - розв’язки, тоді y = c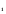 cos(x)+c
cos(x)+c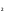 sin(x) - розв’язок .
sin(x) - розв’язок .
3. Необхідні і достатні умови лінійної незалежності n-розв’язків лінійного однорідного диференціального рівняння n – го порядку.
Означення 5.4. Функції  (x),
(x),  (x), ... ,
(x), ... , 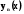 називаються лінійно незалежними на (a,b) , якщо між не існує співвідношення виду
називаються лінійно незалежними на (a,b) , якщо між не існує співвідношення виду
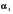
 (x) +
(x) + 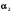
 (x) + ... +
(x) + ... + 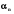
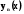
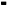 0 , a < x < b , (5.13)
0 , a < x < b , (5.13)
де 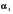 , ... ,
, ... , 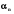 - постійні числа не рівні нулю одночасно . В противному випадку функції
- постійні числа не рівні нулю одночасно . В противному випадку функції  (x),
(x),  (x), ... ,
(x), ... , 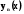 називають лінійно залежними на (a,b).
називають лінійно залежними на (a,b).
Для двох функцій поняття лінійної незалежності на (a,b) зводиться до того, щоб відношення функцій 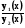 ,
, 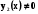 не було постійним на (a,b).
не було постійним на (a,b).
Зауваження 5.1. Якщо одна із функцій на (a,b) тотожньо дорівнює нулю, то ці функції лінійно залежні.
Приклад 5.3. Функції  =1,
=1,  =x, ... ,
=x, ... , 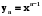 - лінійно незалежні на будь-якому інтервалі (a,b)
- лінійно незалежні на будь-якому інтервалі (a,b) 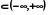 . Дійсно співвідношення
. Дійсно співвідношення
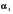 +
+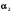 x + ... +
x + ... + 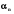 x
x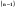 =0 , в якому не всі
=0 , в якому не всі 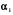 дорівнюють нулю, не може виконуватися для будь-яких x , так як рівняння (n-1) – го степеня має не більше (n-1) – го коренів.
дорівнюють нулю, не може виконуватися для будь-яких x , так як рівняння (n-1) – го степеня має не більше (n-1) – го коренів.
Приклад 5.4. Функції 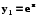 ,
, 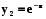 - лінійно незалежні, так як співвідношення
- лінійно незалежні, так як співвідношення 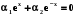 , де
, де 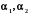 не рівні одночасно нулю, виконуються не більше ніж в одній точці. Це випливає з
не рівні одночасно нулю, виконуються не більше ніж в одній точці. Це випливає з 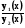 =
=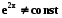 .
.
Приклад 5.5. Функції  =sin
=sin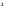 x ,
x ,  =cos
=cos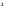 x ,
x , 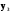 =1 – лінійно залежні на
=1 – лінійно залежні на 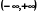 , так як для будь-якого х справджується співвідношення
, так як для будь-якого х справджується співвідношення
sin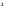 x + cos
x + cos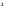 x – 1 = 0 .
x – 1 = 0 .
Розглянемо необхідні умови лінійної залежності n - функцій .
Теорема 5.1. Якщо функції  (x),
(x),  (x), ... ,
(x), ... , 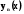 - лінійно залежні на (a,b) , то їх вронскіан W (x) тотожньо дорівнює нулю на (a,b) . Тут
- лінійно залежні на (a,b) , то їх вронскіан W (x) тотожньо дорівнює нулю на (a,b) . Тут
W (x) = 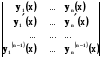 (5.14)
(5.14)
Доведення. Згідно умови теореми
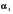
 (x) +
(x) + 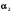
 (x) + ... +
(x) + ... + 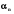
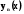
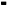 0 , a < x < b , де не всі
0 , a < x < b , де не всі 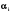 одночасно рівні нулю . Нехай
одночасно рівні нулю . Нехай 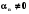 , тоді
, тоді
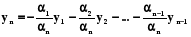 (5.15)
(5.15)
Диференціюємо (5.15) (n-1)-раз і підставляємо в (5.14)
W (x) =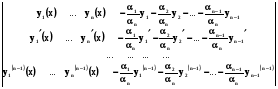 (5.16)
(5.16)
Розкладаючи визначник (5.16) на суму визначників, будемо мати в кожному з них два однакові стовпці, тому всі визначники будуть рівні нулю і отже
W (x) 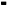 0 , a < x < b. Теорема доведена.
0 , a < x < b. Теорема доведена.
Нехай кожна з функцій  (x),
(x),  (x), ... ,
(x), ... , 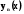 - розв’язок диференціального рівняння (5.5) . Тоді необхідні і достатні умови лінійної незалежності цих
- розв’язок диференціального рівняння (5.5) . Тоді необхідні і достатні умови лінійної незалежності цих
розв’язків даються теоремою 5.1. і слідуючою теоремою .
Теорема 5.2. Якщо функції  (x),
(x),  (x), ... ,
(x), ... , 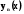 - суть лінійно незалежні розв’язки диференціального рівняння (5.5), всі коефіцієнти якого неперервні на (a,b) , то вронскіан цих розв’язків W не дорівнює нулю в жодній точці інтервалу (a,b) .
- суть лінійно незалежні розв’язки диференціального рівняння (5.5), всі коефіцієнти якого неперервні на (a,b) , то вронскіан цих розв’язків W не дорівнює нулю в жодній точці інтервалу (a,b) .
Доведення. Припустимо протилежне , що в точці 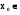 (a,b)
(a,b) 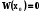 . Складемо систему рівнянь
. Складемо систему рівнянь
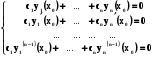 (5.17)
(5.17)
Так як визначник системи (5.17) 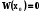 , то вона має ненульовий розв’язок
, то вона має ненульовий розв’язок
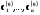 . Розглянемо функцію y =
. Розглянемо функцію y = 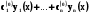 , (5.18)
, (5.18)
яка являється розв’язком диференціального рівняння (5.5).
Система (5.17) показує , що в точці 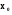 розв’язок (5.18) перетворюється в нуль разом із своїми похідними до (n-1) –го порядку . В силу теореми існування і єдиності це значить , що має місце тотожність y (x) =
розв’язок (5.18) перетворюється в нуль разом із своїми похідними до (n-1) –го порядку . В силу теореми існування і єдиності це значить , що має місце тотожність y (x) = 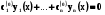 , a < x < b, де не всі
, a < x < b, де не всі 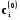 дорівнюють нулю . Останнє означає , що розв’язки
дорівнюють нулю . Останнє означає , що розв’язки  (x),
(x),  (x), ... ,
(x), ... , 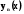 - лінійно залежні на (a,b). Це протиріччя і доводить теорему.
- лінійно залежні на (a,b). Це протиріччя і доводить теорему.
З теорем 5.1. і 5.2. випливає : для того , щоб n розв’язків диференціального рівняння (5.5) були лінійно незалежними на (a,b) необхідно і достатньо , щоб їх вронскіан не дорівнював нулю в жодній точці цього інтервалу.
Виявляється , для вияснення лінійної незалежності n розв’язків диференціального рівняння (5.5) достатньо переконатися , що W (x) не дорівнює нулю хоча б в одній точці інтервалу (a,b) . Це випливає з наступних властивостей вронскіана від n розв’язків диференціального рівняння (5.5):
а) Якщо вронскіан дорівнює нулю в одній точці 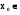 (a,b) і всі коєфіцієнти диференціального рівняння (5.5) являються неперервними , то
(a,b) і всі коєфіцієнти диференціального рівняння (5.5) являються неперервними , то 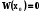 на (a,b).
на (a,b).
Дійсно, якщо 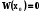 , то по теоремі 5.2. функції
, то по теоремі 5.2. функції  (x),
(x),  (x), ... ,
(x), ... , 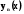 - лінійно залежні на (a,b). Тоді , по теоремі 5.1.
- лінійно залежні на (a,b). Тоді , по теоремі 5.1.  на (a,b);
на (a,b);
б) якщо вронскіан n розв’язків диференціального рівняння (5.5) відмінний від нуля в одній точці 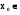 (a,b) , то
(a,b) , то 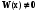 на (a,b) .
на (a,b) .
Дійсно , якби W (x) дорівнював в одній точці з (a,b) нулю , то згідно а)  на (a,b) , в тому числі і в точці
на (a,b) , в тому числі і в точці 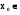 (a,b) , що протирічить умові.
(a,b) , що протирічить умові.
Звідси випливає , якщо n розв’язків диференціального рівняння (5.5) лінійно незалежні на (a,b) , то вони будуть лінійно незалежні на будь-якому 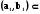 (a,b) .
(a,b) .
4. Формула Остроградського – Ліувілля.
Ця формула має вигляд 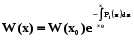 (5.19)
(5.19)
Доведення . Розглянемо вронскіан W (x) = 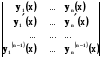 і обчислимо його похідну
і обчислимо його похідну
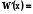
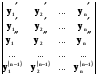
 +
+ 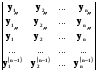 +
+ 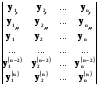 .
.
Перших (n-1)-визначників рівні нулю , так як всі вони мають по дві однакових стрічки . Далі домножимо (n-1) стрічки останнього визначника відповідно на 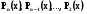 і складемо всі n стрічок . В силу диференціального рівняння (5.5) маємо
і складемо всі n стрічок . В силу диференціального рівняння (5.5) маємо 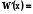
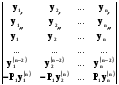 =
=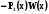 ,
,
Звідки маємо формулу (5.19) .
5. Фундаментальна система розв’язків та ії існування.
Означення 5.5. Сукупність n розв’язків диференціального рівняння (5.5) визначених і лінійно незалежних на (a,b) називається фундаментальною системою розв’язків .
З попереднього випливає , для того , щоб система n розв’язків диференціального рівняння (5.5) була фундаментальною системою розв’язків необхідно і достатньо , щоб вронскіан цих розв’язків був відмінний від нуля хоч в одній точці інтервалу неперервності коефіцієнтів диференціального рівняння (5.5) . Всі ці розв’язки повинні бути бути ненульовими .
Теорема 5.3. (про існування ФСР) Якщо коефіцієнти диференціального рівняння (5.5) являються неперервними на (a,b) , то існує фундаментальна система розв’язків на цьому інтервалі.
Доведення . Візьмемо точку 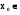 (a,b) і побудуємо, використовуючи метод Пікара , розв’язки :
(a,b) і побудуємо, використовуючи метод Пікара , розв’язки :
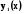 з початковими умовами
з початковими умовами 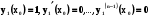 ;
;
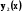 ------------- // ---------------
------------- // --------------- 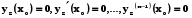 ;
;
... ------------- // --------------- ... ... ... ....
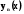 ------------- // ---------------
------------- // --------------- 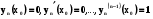 .
.
Очевидно , що 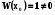 , отже побудовані розв’язки лінійно незалежні .
, отже побудовані розв’язки лінійно незалежні .
Теорема доведена .
З методу побудови лінійно незалежних функцій випливає, що таких функцій можна побудувати безліч.
Побудована система розв’язків називається нормованою в точці 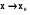 .
.
Для будь-якого диференціального рівняння (5.5) існує тільки одна фундаментальна система розв’язків , нормована по моменту 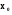 .
.
6. Загальний розв’язок. Число лінійно незалежних розв’язків.
Теорема 5.4. Якщо  (x),
(x),  (x), ... ,
(x), ... , 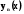 - фундаментальна система розв’язків диференціального рівняння (5.5) , то формула
- фундаментальна система розв’язків диференціального рівняння (5.5) , то формула
y =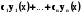 , (5.20) де
, (5.20) де 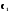 ,
, 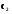 , ... ,
, ... , 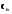 - довільні константи, дає загальний розв’язок диференціального рівняння (5.5) в області a < x < b,
- довільні константи, дає загальний розв’язок диференціального рівняння (5.5) в області a < x < b,
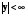 ,
, 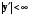 , ... ,
, ... ,  (5.21) , тобто в області визначення
(5.21) , тобто в області визначення
диференціального рівняння (5.5).
Доведення. Якщо  (x),
(x),  (x), ... ,
(x), ... , 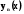 - розв’язки диференціального рівняння (5.5) , то лінійна комбінація (5.20) теж розв’язок .
- розв’язки диференціального рівняння (5.5) , то лінійна комбінація (5.20) теж розв’язок .
Систему 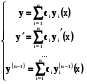 (5.22) можна розв’язати відносно
(5.22) можна розв’язати відносно 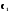 ,
, 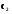 , ... ,
, ... , 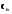
в області (5.21) , так як 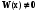 . Згідно визначення (5.20) – загальний розв’язок і він містить в собі всі розв’язки диференціального рівняння (5.5) .
. Згідно визначення (5.20) – загальний розв’язок і він містить в собі всі розв’язки диференціального рівняння (5.5) .
Теорема доведена .
Для знаходження частинного розв’язку такого , що 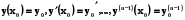 (5.23)
(5.23)
необхідно все підставити в (5.22) і визначити 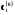 , i=1,2,…,n .
, i=1,2,…,n .
Тоді 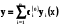 - частинний розв’язок , якщо фундаментальна система розв’язків – нормована в точці
- частинний розв’язок , якщо фундаментальна система розв’язків – нормована в точці 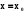 , то
, то 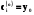 , тобто
, тобто
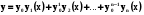 (5.24) загальний розв’язок в формі Коші .
(5.24) загальний розв’язок в формі Коші .
Зауважимо , що загальний розв’язок диференціального рівняння (5.5) є однорідна лінійна функція від довільних констант .
Твердження 5.1. Диференціальне рівняння (5.5) не може мати більше ніж n лінійно незалежних частинних розв’язків.
Дійсно , нехай ми маємо (n+1) частинний розв’язок . Розглянемо n перших . Якщо вони лінійно залежні , то і всі будуть лінійно залежні , так як
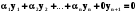 , a < x < b, де всі
, a < x < b, де всі 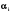 не дорівнють нулю . Якщо ж вони лінійно залежні, то по теоремі 5.4. будь-який розв’язок , в тому числі і
не дорівнють нулю . Якщо ж вони лінійно залежні, то по теоремі 5.4. будь-який розв’язок , в тому числі і 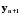 виражається через
виражається через  ,
,  , ... ,
, ... , 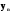 , тобто
, тобто 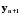 =
=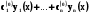 . Так , що (n+1)-ий розв’язок знову виявився лінійно залежним .
. Так , що (n+1)-ий розв’язок знову виявився лінійно залежним .
Для побудови диференціального рівняння типу (5.5) по системі лінійно незалежних функцій  (x),
(x),  (x), ... ,
(x), ... , 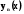 , які n раз неперервно диференційовані на (a,b) , вронскіан яких
, які n раз неперервно диференційовані на (a,b) , вронскіан яких 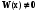 ,
, 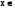 (a,b) необхідно розглянути вронскіан порядку (n+1)
(a,b) необхідно розглянути вронскіан порядку (n+1)
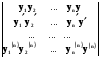 = 0
= 0
і розкрити цей визначник по останньому стовпцю .
Якщо відомо один частинний ненульовий розв’язок диференціального рівняння (5.5) , то можна понизати порядок його на одиницю заміною
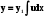 , або
, або 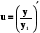 (5.25)
(5.25)
Тоді 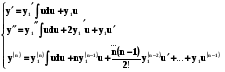
і диференціального рівняння (5.5) запишемо у вигляді
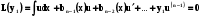
Ми отримали диференціальне рівняння порядку (n-1) .
Якщо маємо к лінійно незалежнихчастинних розв’язків , то диференціальне рівняння (5.5) можна понизити на к одиниць .

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ