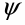
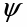
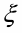
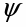
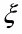IX математический симпозиум.

Закономерность распределения простых чисел в ряду натуральных чисел.

г. Волжский.

05-11 октября 2008 года.

Белотелов В.А.

Нижегородская обл.

г. Заволжье

vbelotelov@mail. ru

Простые числа? – Это просто!?

Узнав о важной роли простых чисел (ПЧ) в криптографии, генерации случайных чисел, навигации, имитационном моделировании и о том, что нужна закономерность распределения ПЧ в ряду натуральных чисел, не являясь математиком, всё же рискнул заняться решением этой задачи. Результат ниже.

Для начала выписал ряд ПЧ. Конечно же, это было сделано с целью заметить, хоть какую бы, закономерность. С этой же целью были вычислены разности между соседними числами ряда ПЧ. Было замечено, что иногда появлялась последовательность разностей 6-4-2-4-2-4-6-2. Там, где эта последовательность нарушалась, были введены составныё числа (СЧ). Результат представлен в таблице 1, СЧ в которой подчёркнуты. Числа 2, 3, 5, являясь ПЧ, из рассмотрения всё же были убраны. Это первое исключение из правил. Вторая вольность заключалась введением в рассмотрение числа 1, зная, что единица не является простым числом.

Целью же было найти закономерность среди ПЧ + СЧ, а потом уже найти закономерность среди ПЧ. Стратегия поиска закономерности ПЧ заключалась в следующей логической формуле:

(закономерность ПЧ+СЧ) – (закономерность СЧ) = закономерность ПЧ.

Из ПЧ + СЧ, представленных в таблице 1, была составлена система из восьми арифметических прогрессий. Результат представлен в таблице 2.

Разности всех восьми прогрессий равны 30 и их первые члены равны соответственно 1, 7, 11, 13, 17, 19, 23, 29, а сами ряды обозначены через R1, R7,R11, R13, R17, R19, R23, R29. СЧ, как и в таблице 1, подчёркнуты и сверху расписаны в виде произведений двух чисел. Можно сформулировать правило, по которому в любой из восьми арифметических прогрессий распределены СЧ.

Если в арифметической прогрессии, какой – либо член an можно представить в виде двух сомножителей fxp, то последующие члены этой прогрессии an+mf являются произведением fx(p+md), а члены an+kp произведением px(f+kd), где m и k любые натуральные

числа, а d – разность этой прогрессии.

Данное правило не нуждается в доказательстве, т. к. фактически следует из определения арифметической прогрессии. Но для обеспечения закономерности ПЧ имеет большое значение. Во - первых, оно запрещает поиск рядов ПЧ, подчиняющихся одной арифметической прогрессии, т. к. любое простое число an можно представить в виде anх1, и тогда в любом ряде через число членов an, появляется составное число anх(1+d).

Во – вторых, в любой арифметической прогрессии появление дополнительных составных чисел возможно только в сочетании с разностью именно этой прогрессии.

Это правило можно сформулировать для любого числа сомножителей, но в данном случае интерес представляет число сомножителей равное двум.

В качестве примера рассмотрим в ряде R1 четвёртый член равный 91=7х13. Ближайшим членом в ряде R1 кратным семи является число 301, отстоящее от числа 91 на семь номеров, соответственно, число 301 принадлежит ряду СЧ. Число 301 является произведением 7х43 (301=7х43), и с номера этого числа равного 11, каждое сорок третье число, тоже делится на 43 и, соответственно, принадлежит к ряду СЧ. Дальше это можно не описывать, т. к. это хорошо видно в таблице 2.

Расписав таблицу 2 в виде математических символов, удалось получить систему из восьми формул, расписанных в виде разности сумм, см. таблицу 3. Во всех восьми формулах системы, члены с рядами двойных сумм служат фильтрами, удаляющими СЧ из ряда ПЧ+СЧ, и задают работу фильтров в виде матриц.

В таблице 4 изображено распределение номеров СЧ в ряде R1, определяемых вторым членом формулы. Это матрица, в которой и по столбцам и по строкам арифметические прогрессии.

В формулах индексы 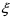и 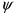обозначают столбцы и строки подобных матриц, сами же и дополнительными индексами не отягощаю. Без и описать работу матриц не смог, а формальная фраза, что в выражении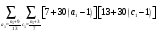под суммой произведений подразумеваются всевозможные их комбинации в зависимости от значений a1 и с1, будет неверна. Ибо все члены с номерами при >1 и >1 из формулы выпадают.

Система формул арифметических прогрессий, позволяющая вычислять ПЧ, получилась достаточно громоздкой, но закономерность обозначена.

Данная статья была подготовлена для публикации в научном журнале с математическим уклоном. Пока шёл поиск данного журнала, путём несложных умозаключений, была составлена система рядов арифметических прогрессий с разностью 10. Результат в таблице 5 и 6. Всё было расписано по образцу и подобию предыдущего материала. В таблице 7 изображена матрица для номеров второго члена формулы 1 таблицы 6.

Не начав переписывать статью заново, в связи с открытием новой системы уравнений, опять же путём размышлений, были расписаны арифметические прогрессии с разностью 2 и 1, т.е. при разности единица ПЧ были напрямую увязаны с натуральным рядом. Результат в таблице 8 и 9.

Всё расписано, как и в случаях с системами уравнений арифметических прогрессий разностей 30 и 10. И после этого наступил момент истины.

Оказалось, что подобных уравнений можно составить бесконечное множество. Навскидку – это арифметические прогрессии с разностью 1, 2, 4, 6, 10, 12, 18, 20, 30, 36, 60, и т.д. Даже в перечисленном до разности 60 указаны не все.

Обобщающий вывод:

ПЧ можно представить комбинацией арифметических прогрессий. Таких комбинаций бесконечное множество. Но каждая из комбинаций систем арифметических прогрессий позволяет только единственное представление ПЧ при заданной разности прогрессий задающий ряды ПЧ+СЧ.

1

7

11

13

17

19

23

29

31

37

41

43

47

49

53

59

6

4

2

4

2

4

6

2

6

4

2

4

2

4

6

2

61

67

71

73

77

79

83

89

91

97

101

103

107

109

113

119

6

4

2

4

2

4

6

2

6

4

2

4

2

4

6

2

121

127

131

133

137

139

143

149

151

157

161

163

167

169

173

179

6

4

2

4

2

4

6

2

6

4

2

4

2

4

6

2

181

187

191

193

197

199

203

209

211

217

221

223

227

229

233

239

6

4

2

4

2

4

6

2

6

4

2

4

2

4

6

2

241

247

251

253

257

259

263

269

271

277

281

283

287

289

293

299

6

4

2

4

2

4

6

2

6

4

2

4

2

4

6

2

301

307

311

313

317

319

323

329

331

337

341

343

347

349

353

359

6

4

2

4

2

4

6

2

6

4

2

4

2

4

6

2

361

367

371

373

377

379

383

389

391

397

401

403

407

409

413

419

6

4

2

4

2

4

6

2

6

4

2

4

2

4

6

2

421

427

431

433

437

439

443

449

451

457

461

463

467

469

473

479

6

4

2

4

2

4

6

2

6

4

2

4

2

4

6

2

481

487

491

493

497

499

503

509

511

517

521

523

527

529

533

539

6

4

2

4

2

4

6

2

6

4

2

4

2

4

6

2

541

547

551

553

557

559

563

569

571

577

581

583

587

589

593

599

6

4

2

4

2

4

6

2

6

4

2

4

2

4

6

2

601

607

611

613

617

619

623

629

631

637

641

643

647

649

653

659

6

4

2

4

2

4

6

2

6

4

2

4

2

4

6

2

661

667

671

673

677

679

683

689

691

697

701

703

707

709

713

719

6

4

2

4

2

4

6

2

6

4

2

4

2

4

6

2

721

727

731

733

737

739

743

749

751

757

761

763

767

769

773

779

6

4

2

4

2

4

6

2

6

4

2

4

2

4

6

2

7х13

11х11

7х43

19х19

17х23

11х41

13х37

7х73

1

31

61

91

121

151

181

211

241

271

301

331

361

391

421

451

481

511

541

571

11х17

7х31

13х19

7х61

11х47

7

37

67

97

127

157

187

217

247

277

307

337

367

397

427

457

487

517

547

577

7х23

13х17

11х31

7х53

19х29

7х83

11

41

71

101

131

161

191

221

251

281

311

341

371

401

431

461

491

521

551

581

7х19

11х23

7х49

13х31

17х29

7х79

11х53

13

43

73

103

133

163

193

223

253

283

313

343

373

403

433

463

493

523

553

583

7х11

7х41

13х29

11х37

19х23

7х71

17х31

17

47

77

107

137

167

197

227

257

287

317

347

377

407

437

467

497

527

557

587

7х7

13х13

7х37

17х17

11х29

7х67

23х23

13х43

19х31

19

49

79

109

139

169

199

229

259

289

319

349

379

409

439

469

499

529

559

589

11х13

7х29

17х19

7х59

11х43

13х41

23

53

83

113

143

173

203

233

263

293

323

353

383

413

443

473

503

533

563

593

7х17

11х19

13х23

7х47

11х49

7х77

29

59

89

119

149

179

209

239

269

299

329

359

389

419

449

479

509

539

569

599

R1

R7

R11

R13

R17

R19

R23

R29

7х103

11х71

29х29

13х67

17х53

19х49

7х133

31х31

23х47

11х101

7х163

601

631

661

691

721

751

781

811

841

871

901

931

961

991

1021

1051

1081

1111

1141

1171

13х49

7х91

23х29

17х41

19х43

11х77

7х121

13х79

7х151

31х37

11х107

607

637

667

697

727

757

787

817

847

877

907

937

967

997

1027

1057

1087

1117

1147

1177

13х47

11х61

17х43

7х113

23х37

13х77

11х91

7х143

19х59

611

641

671

701

731

761

791

821

851

881

911

941

971

1001

1031

1061

1091

1121

1151

1181

19х37

7х109

13х61

11х83

23х41

7х139

17х59

13х91

7х169

613

643

673

703

733

763

793

823

853

883

913

943

973

1003

1033

1063

1093

1123

1153

1183

7х101

11х67

13х59

7х131

19х53

17х61

11х97

23х49

7х161

13х89

617

647

677

707

737

767

797

827

857

887

917

947

977

1007

1037

1067

1097

1127

1157

1187

11х59

7х97

17х47

7х127

13х73

11х89

7х157

19х61

29х41

619

649

679

709

739

769

799

829

859

889

919

949

979

1009

1039

1069

1099

1129

1159

1189

7х89

23х31

11х73

17х49

7х119

19х47

13х71

7х149

29х37

11х103

623

653

683

713

743

773

803

833

863

893

923

953

983

1013

1043

1073

1103

1133

1163

1193

17х37

13х53

7х107

19х41

11х79

29х31

7х137

23х43

13х83

17х67

7х167

11х109

629

659

689

719

749

779

809

839

869

899

929

959

989

1019

1049

1079

1109

1139

1169

1199

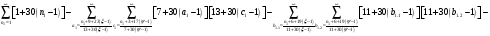
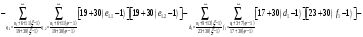
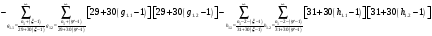
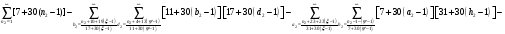
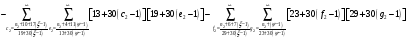
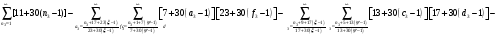
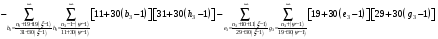
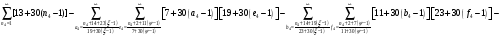
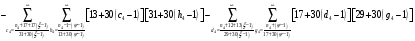
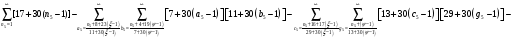
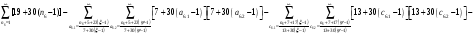
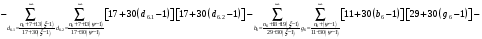
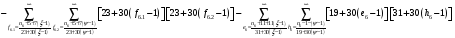
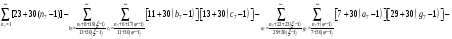
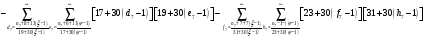
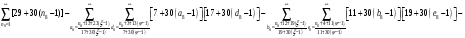
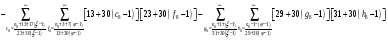
+13

+13

4

+7

11

+7

18

+7

25

+7

32

39

46

53

60

67

…

+13

+43

+73

+103

+133

+163

+193

+223

+253

+283

17

+37

54

+37

91

+37

128

165

202

239

276

313

350

…

+43

+73

+103

30

+67

97

+67

164

+67

231

298

365

432

499

566

633

…

+13

+43

+73

+103

43

+97

140

+97

237

+97

334

431

528

625

722

819

916

…

56

+127

183

310

437

564

691

818

945

1072

1199

…

69

+157

226

383

540

697

854

1011

1168

1325

1482

…

82

+187 

269

456

643

830

1017

1204

1391

1578

1765

…

95

+217 

312

529

746

963

1180

1397

1614

1831

2048

…

108

+247 

355

602

849

1096

1343

1590

1837

2084

2331

…

121

+277

398

675

952

1229

1506

1783

2060

2337

2614

…

…

…

…

…

…

…

…

…

…

…

3х7

3х17

9х9

3х27

7х13

3х37

11х11

3х47

7х23

9х19

3х57

3х67

1

11

21

31

41

51

61

71

81

91

101

111

121

131

141

151

161

171

181

191

201

3х11

7х9

3х21

3х31

3х41

7х19

11х13

9х17

3х51

3х61

7х29

3

13

23

33

43

53

63

73

83

93

103

113

123

133

143

153

163

173

183

193

203

3х9

3х19

7х11

3х29

9х13

3х39

7х21

3х49

3х59

11х17

9х23

3х69

7

17

27

37

47

57

67

77

87

97

107

117

127

137

147

157

167

177

187

197

207

3х3

3х13

7х7

3х23

9х11

3х33

7х17

3х43

3х53

13х13

9х21

7х27

3х63

11х19

9

19

29

39

49

59

69

79

89

99

109

119

129

139

149

159

169

179

189

199

209

R1

R1

R3

R7

R9

R3

R9

R7

R1

13х17

11х21

7х33

3х77

9х29

3х87

3х97

7х43

3х107

11х31

9х39

13х27

3х117

19х19

7х53

3х127

17х23

211

221

231

241

251

261

271

281

291

301

311

321

331

341

351

361

371

381

391

R3

9х27

3х71

9х27

3х81

11х23

7х39

3х91

3х101

17х19

9х37

3х111

7х49

11х33

3х121

3х131

213

223

233

243

253

263

273

283

293

303

313

323

333

343

353

363

373

383

393

9х27

11х27

R7

9х33

7х31

3х79

13х19

3х89

7х41

11х27

9х33

3х99

3х109

17х21

7х51

3х119

13х29

9х43

3х129

217

227

237

247

257

267

277

287

297

307

317

327

337

347

357

367

377

387

397

9х27

R9

3х73

3х83

7х37

9х31

3х93

17х17

13х23

3х103

11х29

7х47

19х21

3х113

9х41

3х123

7х57

3х133

219

229

239

249

259

269

279

289

299

309

319

329

339

349

359

369

379

389

399

R1

R3

R9

R7

R1

3х137

9х49

21х21

7х63

3х147

11х41

3х157

13х37

3х167

7х73

9х59

3х177

19х29

11х51

17х33

3х187

7х83

401

411

421

431

441

451

461

471

481

491

501

511

521

531

541

551

561

571

581

R3

7х59

9х47

3х141

3х151

11х43

7х69

21х23

3х161

17х29

19х27

9х57

3х171

3х181

7х79

3х191

11х53

403

413

423

433

443

453

463

473

483

493

503

513

523

533

543

553

563

573

583

7х81

9х63

R7

11х37

3х139

7х61

19х23

3х149

9х53

3х159

7х71

3х169

11х47

17х31

3х179

7х81

9х63

3х189

407

417

427

437

447

457

467

477

487

497

507

517

527

537

547

557

567

577

587

R9

11х39

3х143

9х51

17х27

3х153

7х67

3х163

3х173

23х23

11х49

7х77

9х61

3х183

3х193

19х31

409

419

429

439

449

459

469

479

489

499

509

519

529

539

549

559

569

579

589

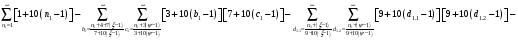
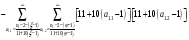
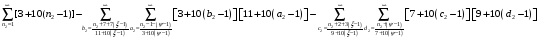
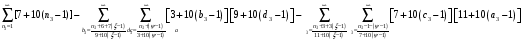
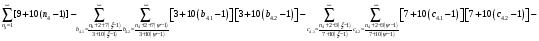
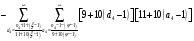
3

+3

6

+3

9

+3

12

+3

15

18

21

24

27

30

…

+7

+17

+27

+37

+47

+57

+67

+77

+87

+97

10

+13

23

+13

36

+13

49

62

75

88

101

114

127

…

+7

+17

+27

+37

+47

17

+23

40

+23

63

+23

86

109

132

155

178

201

224

…

+7

+17

+27

+37

+47

24

+33

57

+33

90

+33

123

156

189

222

255

288

321

…

+7

31

+43

74

117

160

203

246

289

332

375

418

…

38

+53

91

144

197

250

303

356

409

462

515

…

45

+63 

108

171

234

297

360

423

486

549

612

…

52

+73 

125

198

271

344

417

490

563

636

709

…

59

+83 

142

225

308

391

474

557

640

723

806

…

66

+93

159

252

345

438

531

624

717

810

903

…

…

…

…

…

…

…

…

…

…

…

3х3

an_i =2n - 1

1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61 …

5

+3

8

+3

11

+3

14

+3

17

+3

20

+3

23

+3

26

+3

29

…

+3

+5

+7

+9

+11

+13

+15

+17

+19

8

+5

13

18

23

28

33

38

43

48

…

+3

+6

+6

11

+7

18

25

32

39

46

53

60

67

…

+3

14

+9

23

32

41

50

59

68

77

86

…

+3

+6

+7

n ≠

n ≠

17

+11

28

39

50

61

72

83

94

105

…

+3

20

+13

33

46

59

72

85

98

111

124

…

+3

23

+15

38

53

68

83

98

113

128

143

…

+3

26

+17

43

60

77

94

111

128

145

162

…

+3

29

+19

48

67

86

105

124

143

162

181

…

…

…

…

…

…

…

…

…

…

2х2

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32,

33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44 ,45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56. 57, 58, 59, 60, 61 …

an_i = n

4

+2

6

+2

8

+2

10

+2

12

+2

14

+2

16

+2

18

…

+2

+3

+4

+5

+6

+7

+8

+9

6

+3

9

+3

12

+3

15

+3

18

+3

21

+3

24

+3

27

…

+2

+6

+6

8

+4

12

16

20

24

28

32

36

…

+2

n ≠

10

+5

15

20

25

30

35

40

45

…

+2

+6

n ≠

+7

12

+6

18

24

30

36

42

48

54

…

+2

14

+7

21

28

35

42

49

56

63

…

+2

16

+8

24

32

40

48

56

64

72

…

+2

18

+9

27

36

45

54

63

72

81

…

…

…

…

…

…

…

…

…

5х5 7х7 5х11 5х17 7х13 5х23 11х11 7х19 5х29

1, 7, 13, 19, 25, 31, 37, 43, 49, 55, 61, 67, 73, 79, 85, 91, 97, 103, 109, 115, 121, 127, 133, 139, 145,

5х7 5х13 7х11 5х19 7х17 5х25

5, 11, 17, 23, 29, 35, 41, 47, 53, 59, 65, 71 , 77, 83, 89, 95, 101, 107, 113, 119, 125, 131, 137, 143. 149 …

5

+5

10

+5

15

+5

20

+5

25

…

+5

+11

+17

+23

+29

10

+11

21

+11

32

+11

43

+11

54

…

+5

+11

15

+17

32

49

66

83

…

+5

+11

20

+23

43

66

89

112

…

+5

+11

25

+29

54

83

112

141

…

…

…

…

…

…

an_1i =1+ 6 (n₁-1)

an_2j =5+ 6 (n₂-1)

n₁ ≠

Закономерность распределения простых чисел (дополнение).

Белотелов В.А.

Нижегородская обл.

г. Заволжье

vbelotelov@mail. ru

Там где даны в качестве примера разности арифметических прогрессий и указан их ряд 1, 2, 4, 6, 10, 12, 18, 20, 30, 36, 60. На самом деле пропусков в ряду быть не должно. Ряд разностей арифметических прогрессий имеет вид – 1, 2, 3, 4, 5, 6….  .

Я написал предыдущий ряд разностей по принципу личной симпатии. Подстраховался от критики, ежели бы у кого-то не получилось составить систему уравнений, например, с разностью d = 7, ибо для нетренированных рук могут возникнуть трудности.

И ещё. Формулы членов матриц составных чисел (СЧ), которые описываются в системах уравнений двойными суммами. Для этого требуется всего лишь в значения переменных двойных сумм вставить их аналитические выражения через переменные и - столбцы и строки матриц.

Тогда формула любого члена матриц СЧ таблицы 4, примет вид (30I - 17) (30j - 23).

Аналогично для таблицы 7 - (10I - 3) (10 j - 7).

Для таблицы 8, ряда нечётных чисел - (2I + 1) (2 j + 1).

Для таблицы 9, ряда натуральных чисел - (I + 1) ( j + 1).

Заостряю внимание на том факте, что это уже не номера членов СЧ в рядах простых чисел ПЧ + СЧ, а численные значения этих номеров. И подобных уравнений СЧ можно составить по числу систем арифметических прогрессий, и даже значительно больше, т.е. бесконечное множество.

Всё же для наглядности распишу систему уравнений таблицы 3 предыдущей работы.

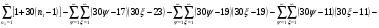
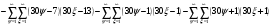
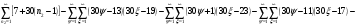
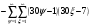
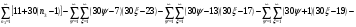
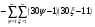
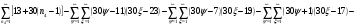
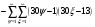
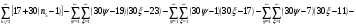
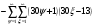
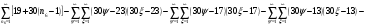
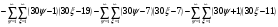
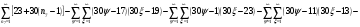
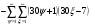
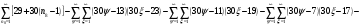
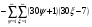
и - столбцы и строки матриц, индексами не снабжаю.

И уж больно симпатичная система из 2-х уравнений с разностью арифметических прогрессий d=6.

5х5

7х7

5х11

5х17

7х13

1

7

13

19

25

31

37

43

49

55

61

67

73

79

85

91

97

5х7

5х13

7х11

5х19

5

11

17

23

29

35

41

47

53

59

65

71

77

83

89

95

101

Напишу только формулы составных чисел

1 – для верхнего ряда (6I - 1) (6 j - 1), (6k + 1) (6e +1).

2 – для нижнего ряда (6I + 1) (6 j - 1).

А написал с единственной целью сравнить формулы разных систем простых чисел.

В системе c d = 30 число 91 – это (30 - 17) (30 - 23), при = 1, = 1.

В системе c d = 10 это же число – (10 - 3) (10 - 7), при = 2, = 1.

В системе c d = 6 ……………… – (6+ 1) (6+ 1), при = 1, = 2.

В системе c d = 4 ……………… – (4 - 1) (4+ 1), при = 2, = 3.

В системе c d = 2 ……………… – (2+ 1) (2+ 1), при = 3, = 6.

В системе c d = 1 ……………… – (+ 1) (+1), при = 6, = 12.

6

+5

11

+5

16

+5

21

+5

26

…

+7

+13

+19

+25

+31

13

+11

24

+11

35

+11

46

+11

57

…

+7

+13

+19

20

+17

37

54

71

88

…

+7

+13

27

+23

50

73

96

119

…

+7

+13

34

+29

63

92

121

150

…

…

…

…

…

…

9

+7

16

+7

23

+7

30

+7

37

…

+7

+13

+19

+25

+31

16

+13

29

+11

42

+11

55

+11

68

…

+7

+11

27

+19

42

61

80

99

…

+7

+11

30

+25

55

80

105

130

…

+7

+11

37

+31

68

99

130

161

…

…

…

…

…

…

n₂ ≠

n₁ ≠