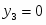
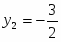
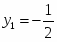
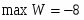
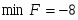
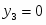
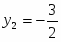
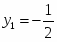
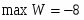
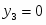
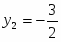
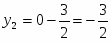
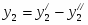
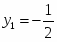
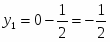
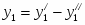
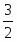
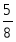
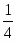
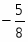
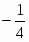
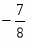
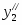
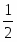
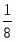
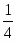
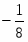
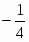
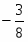
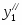
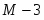
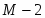
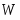
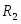
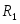
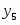
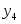
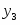
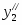
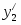
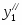
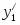
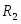
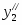
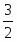
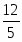
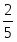
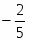
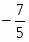
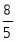
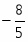
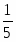
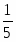
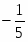
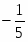
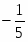
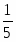
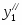
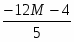
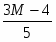
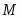
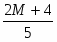
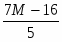
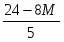
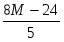
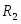
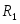
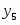
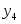
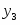
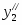
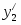
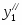
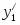
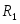
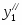
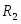
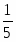
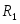
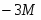
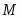
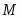
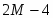
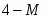
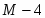
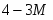
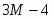
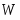
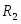
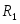
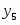
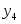
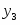
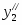
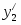
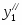
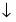
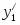
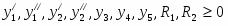
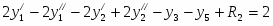
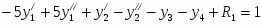
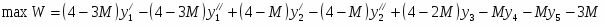
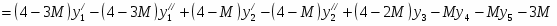
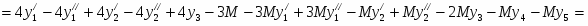
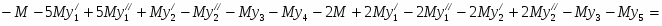
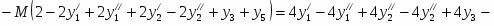
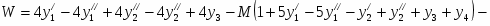
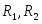
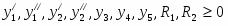
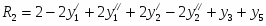
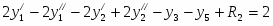
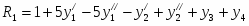
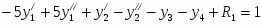
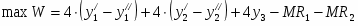
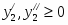
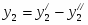
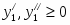
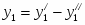
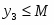
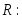
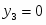
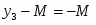
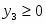
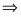
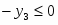
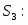
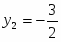
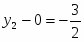
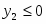
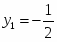
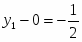
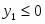
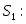
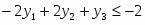
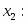
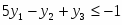
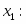
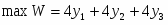
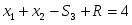
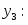
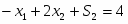
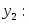
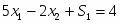
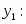
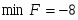
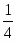
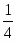
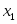
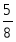
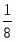
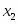
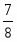
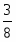
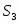
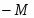
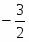
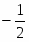
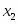
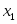
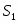
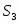
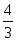
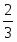
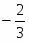
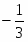
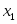
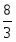
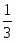
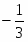
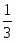
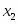
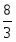
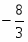
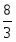
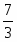
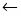
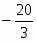
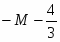
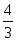
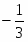
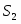
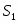
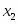
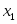
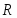
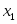
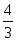
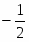
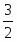
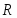
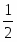
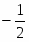
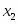
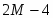
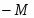
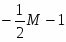
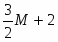
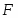
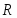
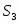
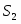
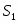
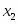
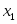
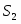
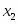
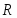
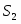
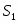
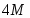
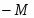
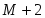
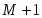
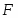
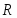
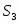
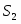
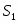
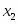
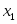
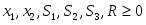
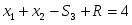
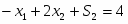
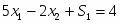
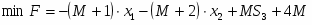
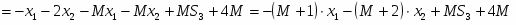
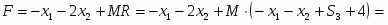
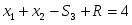
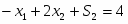
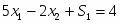
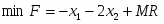
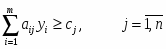
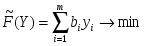
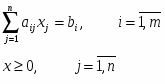
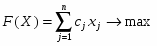
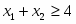
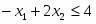
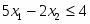
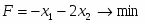Министерство образования и науки Украины

Днепропетровский Национальный Университет

Факультет электроники, телекоммуникаций и компьютерных систем

Кафедра АСОИ

Расчётная задача №4

«Исследование операций»

г. Днепропетровск

2007г.

Задача

Записать задачу двойственную к данной, решить одну из пары задач и отыскать оптимальное решение второй

Прямая задача имеет вид:

Общая постановка двойственной задачи

Двойственная задача – это вспомогательная задача линейного программирования, она формулируется из прямой задачи.

Идея метода основана на связи между решениями прямой и двойственной задачи.

Двойственная задача формируется непосредственно из условий прямой задачи за следующими правилами:

Если прямая задача является задачей максимизации, то двойственная будет задачей минимизации;

Коэффициенты целевой функции прямой задачи С1, С2, ….,Сn становятся свободными членами ограничений двойственной задачи;

Свободные члены ограничений прямой задачи b1, b2, ….,bn становятся коэффициентами целевой функции двойственной задачи;

Матрицу ограничений двойственной задачи получают транспонированием матрицы ограничений прямой задачи;

Если прямая задача является задачей максимизации, то во всех неравенствах двойственной задачи будут стоять знаки ≥, и знаки ≤, если прямая задача является задачей минимизации.

Число ограничений прямой задачи равно числу переменных двойственной задачи.

Прямая задача в канонической форме

Двойственная к ней задача будет иметь вид

Двойственная задача решается симплекс-методом до достижения оптимального решения.

Решение прямой задачи

Все ограничения прямой задачи - это равенства с неотрицательными правыми частями, когда все переменные неотрицательны.

Приведем прямую задачу к стандартному виду:

Подставим значение в целевую функцию:

Таким образом, прямая задача в стандартной форме имеет следующий вид:

Строим симплекс таблицу:

Итерация №1

Базис

Решение

Оценка

0

0

0

5

-2

1

0

0

0

4

-

-1

2

0

1

0

0

4

2

1

1

0

0

-1

1

4

4

- ведущий столбец

- ведущая строка

Итерация №2

Базис

Решение

Оценка

0

0

0

4

0

1

1

0

0

8

2

1

0

0

0

2

-

0

0

-1

1

2

- ведущий столбец

- ведущая строка

Итерация №3

Базис

Решение

Оценка

0

0

0

0

0

1

0

1

0

-

1

0

0

-

- ведущий столбец

- ведущая строка

Итерация №4

Базис

Решение

0

0

0

8

0

0

1

-1

1

0

1

0

0

3

1

0

0

0

2

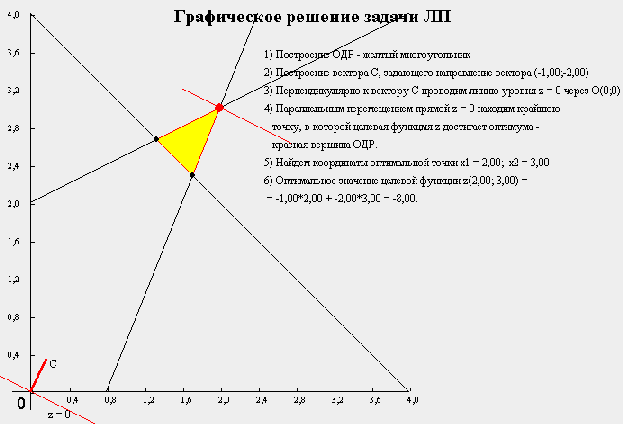
Оптимальное решение прямой задачи:

, Х = {2 , 3}

Решение двойственной задачи

Двойственная задача имеет вид:

Мы получили двойственную задачу и будем решать ее М-методом. Приведем систему линейных неравенств к стандартному виду, перед этим сделав замену:

,

,

Подставим значения в функцию:

Таким образом, двойственная задача в стандартной форме имеет следующий вид:

Симплекс-таблица, итерация 1

Базис

Решение

Оценка

0

0

-5

5

1

-1

-1

-1

0

1

0

1

2

-2

-2

2

-1

0

-1

0

1

2

-

- ведущий столбец

- ведущая строка

Симплекс-таблица, итерация 2

Базис

Решение

Оценка

0

0

0

-1

1

0

0

-

0

0

-1

1

- ведущий столбец

- ведущая строка

Симплекс-таблица, итерация 3

Базис

Решение

0

0

1

0

1

2

3

-8

1

1

0

0

0

0

-1

1

Оптимальное решение двойственной задачи:

, , ,

Ответ

Оптимальное решение прямой задачи: , X = { 2 , 3 }

Для двойственной задачи: , , ,

1