Зависимость высоты дерева от среднегодовой температуры
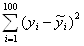
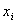
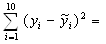
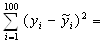
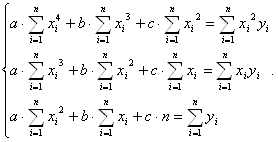
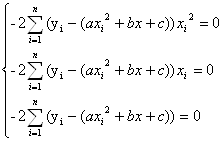
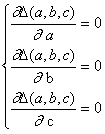
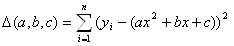
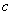
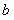
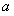
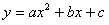
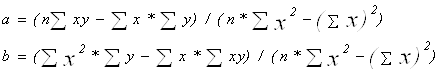
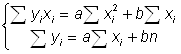
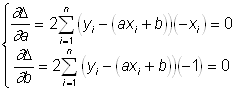
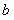
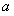
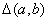
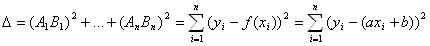
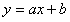
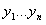
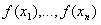
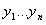
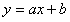
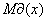
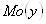
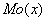
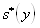
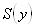
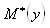
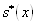
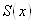
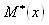
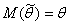
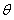
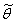
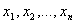
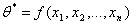
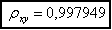
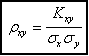
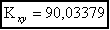
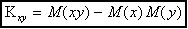
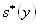
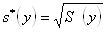
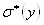
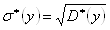
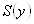
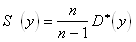
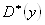
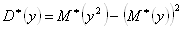
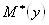
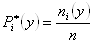
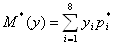
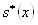
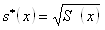
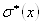
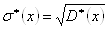
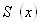
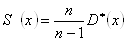

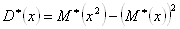
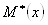
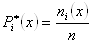
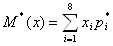
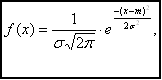
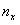
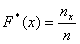
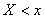
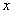
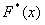
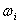
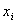
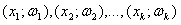
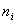
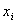
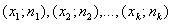
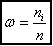
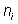
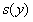
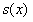
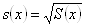
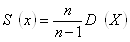
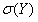
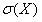
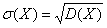
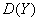
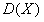
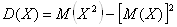
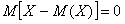
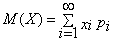
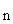
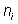
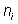
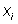 Зависимость высоты дерева от среднегодовой температуры
Зависимость высоты дерева от среднегодовой температуры
Международный университет природы, общества и человека «Дубна»
КУРСОВАЯ РАБОТА
по теории вероятностей
на тему:
Зависимость высоты дерева от среднегодовой температуры
Руководители:
ассистент
Дубна
Содержание
Введение
Постановка задачи
Теоретическая часть
Исходные данные и их обработка
Метод наименьших квадратов
Вывод
Список используемой литературы
Введение
Деревья делятся по виду листьев на хвойные и широколиственные.
Хвойные отличаются обычно жёсткими вечнозелёными игловидными или чешуйчатыми листьями, называемыми хвоей или иглами, образуют шишки или можжевеловых ягод. К этой группе относятся, например, сосны, ели, пихты, лиственницы, кипарисы, секвойи.
Широколиственные деревья имеют широкие и плоские листья — у которых толщина значительно меньше длины и ширины, обычно опадающие раз в год. Широколиственные (или просто лиственные) деревья обычно цветут и плодоносят. К этой группе относятся клёны, буки, ясени, эвкалипты и т. д.
Кроме классификации по виду листьев, деревья делятся по сроку жизни листьев — на листопадные и вечнозелёные.
Листопадные деревья имеют чёткую смену лиственного покрова: все листья на дереве теряют зелёную окраску и опадают, некоторое время (зимой) дерево стоит без листьев, потом (весной) из почек вырастают новые листья.
Вечнозелёные деревья не имеют чёткой смены лиственного покрова: листва находится на дереве в любой момент года, и смена листьев происходит постепенно, в течение всей жизни дерева.
Кроме биологической классификации деревья делятся и по другим признакам: например, плодовые деревья (плоды которых используются человеком в пищу), ценные (древесина которых используется для промышленных целей), корабельные (используемые в кораблестроении), тропические (ареал обитания которых проходит недалеко от экватора), северные (ареал обитания которых проходит далеко от экватора) и т. д.
Высота дерева, расстояние от корневой шейки до конца вершины. Деревья выше 20 метров условно называют деревьями первой величины, от 10 метров до 20 второй величины и до 10 метров – третьей величины.
Методы измерения деревьев
Теневой Метод - стенд рядом с деревом или объектом, который будет измерен. Для лучших результатов, сделайте этот метод в яркий, солнечный день. Если небо является пасмурным, может быть трудно сказать точно, где наконечник тени.
Мера длина Вашей тени. Используйте рулетку или критерий (правитель метра), чтобы измерить Вашу тень от Ваших ног до наконечника Вашей тени. Если у Вас нет кого-то, чтобы помочь Вам, Вы можете отметить конец тени, бросая скалу на это, в то время как Вы стоите. Или еще лучше, помещают скала где-нибудь в основание, и затем положение самостоятельно, таким образом наконечник Вашей тени в скале; тогда мера от того, где Вы стоите скале.
Мера длина тени дерева. Используйте свою ленту измерения, чтобы определить длину тени дерева от основы дерева к наконечнику тени. Это работает лучше всего, если основание все время по тени - справедливо уровень; если дерево будет на наклоне, например, то Ваше измерение не будет очень точно. Вы хотите сделать это как можно быстрее после измерения Вашей тени, так как положение солнца в небе (и следовательно теневая длина) медленно но постоянно изменяется.Если у Вас есть помощник, Вы можете держать один конец имеющей размеры ленты, в то время как он или она измеряет тень дерева, и затем Вы можете немедленно измерить свою тень.
Вычисляют высоту дерева при использовании пропорции длины Вашей тени к Вашей высоте. Так как Вы знаете длину тени дерева, и Вы также знаете, что определенная высота (Ваша высота) производит определенную теневую длину (длина Вашей тени), Вы можете определить высоту дерева с небольшой математикой. Умножьте длину тени дерева Вашей высотой, и затем разделите получающееся число на длину Вашей тени. Например, если Вы - 5 футов высокие (1.5 метра), Ваша тень составляет 8 футов (2.4 метра) долго, и тень дерева составляет 100 футов (30.48 метра) долго, высота дерева (100 x 5) / 8
Метод Карандаша: Требует Помощника - Стенд достаточно далеко от дерева, таким образом, Вы можете рассмотреть целую верхушку дерева к основанию — не двигая Вашей головой. Для самого точного измерения Вы должны стоять так, чтобы Вы были на части основания, которое является об уровне с основанием в основе дерева. Ваш взгляд дерева должен быть настолько свободным насколько возможно.
Сделали, чтобы друг стоял около дерева.
Держат карандаш или маленькое, прямо придерживаются (такие как палка краски или правитель) в одной руке и протягивают Вашу руку так, чтобы карандаш был на расстоянии вытянутой руки перед Вами (между Вами и деревом).
Близко один глаз и регулирует карандаш или вниз так, чтобы Вы могли увидеть самую верхушку дерева наверху карандаша. Это является самым легким, если Вы поворачиваете карандаш так, чтобы обостренный пункт указал прямо. Наконечник карандаша должен таким образом только покрыть верхушку дерева в Вашем луче обзора, поскольку Вы смотрите на дерево "через" карандаш.
Продвиньте свой большой палец или вниз карандаш так, чтобы наконечник Вашего ногтя большого пальца руки был союзник основы дерева. Держа карандаш в положении так, чтобы наконечник был союзник вершины дерева (как в шаге 3), двиньте своим большим пальцем к сути в карандаш, который покрывает пункт (снова, поскольку Вы просматриваете карандаш одним глазом), где дерево встречает основание.
Вращают Вашу руку так, чтобы карандаш был горизонтален (параллельный основанию). Держите свою руку проведенной прямо, и удостоверьтесь, что Ваш ноготь большого пальца руки все еще союзник основы дерева.
Сделали, чтобы Ваш друг двинулся так, чтобы Вы могли увидеть его или её ноги "через" пункт Вашего карандаша. Таким образом, ноги Вашего друга должны быть союзник наконечника карандаша. Он или она, возможно, должен двинуться назад, боком, или по диагонали. С тех пор, в зависимости от высоты дерева, Вы, возможно, должны быть на некотором расстоянии от Вашего друга, рассмотреть сигналы руки использования (рукой, которая не держит карандаш), чтобы сказать ему или ей идти дальше, приезжайте ближе, или двиньтесь налево или право.
Мера расстояние между Вашим другом и деревом. Сделайте, чтобы Ваш друг остался в месте или отметил пятно с палкой или скалой. Тогда используйте имеющую размеры ленту, чтобы измерить прямолинейное расстояние между тем пятном и основой дерева. Если у Вас нет имеющей размеры ленты, Вы можете измерить расстояние шагами, хотя это не будет столь точно. Расстояние между Вашим другом и деревом - высота дерева.
Постановка задачи
На основании имеющихся данных провести статистический анализ совокупности заданных чисел. В ходе работы использовать точечные и интервальные оценки параметров генеральной совокупности, а также различные графические представления данных: диаграмму, гистограммы, полигоны, регрессии. Подсчитать некоторые наиболее важные оценки по выборке и корреляционной таблице. На основании этого разработать метод оценки общей характеристики генеральной совокупности, проверить статистические гипотезы, согласовать исходные данные с теорией.
Теоретическая часть
Приведем основные определения и понятия из курса теории вероятностей и математической статистики, которые будут задействованы и использованы в данной работе.
Математическая статистика — наука о математических методах систематизации и использовании статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надёжность и точность выводов, делаемых на основании ограниченного статистического материала (выборки).
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Для того, чтобы по данным выборки можно было судить об изучаемом признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли, т.е. выборка должна быть репрезентативной (представительной). В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если её осуществлять случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку.
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.
Репрезентативность — главное свойство выборки, состоящее в близости её характеристик (состава, средних величин и т.д.) к соответствующим характеристикам генеральной совокупности, из которой отобрана выборка.
Существует тесная связь между математической статистикой и теорией вероятностей.
Теория вероятностей — раздел математики, в котором по данным вероятностям одних случайных событий находят вероятности других событий, связанных каким-либо образом с первыми. Теория вероятностей изучает также случайные величины и случайные процессы. Одна из основных задач теории вероятностей состоит в выяснении закономерностей, возникающих при взаимодействии случайных факторов.
Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. В данном случае мы имеем выборку случайных значений, объем которой равен n=100.
Наблюдаемые значения называются вариантами, а последовательность вариант в возрастающем порядке — вариационным рядом. Частотой называется число, которое показывает, сколько раз встречается данный вариант. Относительной частотой w называется отношение частоты к объёму выборки n.
Случайной величиной X называется величина, которая под влиянием случайных обстоятельств способна принимать различные значения.
Выборкой называется конечная совокупность результатов наблюдений X, X, ... , X, представляющих собой независимые, одинаково распределенные случайные величины.
Случайные величины описываются следующими характеристиками.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Математическое ожидание приближенно равно среднему значению случайной величины, т.е. служит характеристикой среднего значения случайной величины.
Пусть случайная величина X может принимать только значения x1, x2,...,xn, вероятности которых соответственно равны p1, p2,...,pn . Тогда математическое ожидание M(X) случайной величины Х определяется равенством:
M(X) = x1p1 + x2p2 +…+ xnpn .
Если дискретная случайная величина Х принимает счетное множество возможных значений, то
,
причем математическое ожидание существует, если ряд в правой части сходится абсолютно.
В данном случае М(X )= 9,1947, М(Y) = 30,8216.
Существуют также и другие характеристики случайной величины – это дисперсия и среднее квадратичное отклонение.
Для определения дисперсии случайной величины необходимо ввести понятие отклонения случайной величины от ее математического ожидания.
Пусть Х - случайная величина и М(Х) - ее математическое ожидание. Рассмотрим в качестве новой случайной величины разность (Х - М(Х)).
Отклонением называют разность между случайной величиной и ее математическим ожиданием.
При определении дисперсии используется следующее свойство отклонения:
.
Это приводит к тому, что целесообразно заменить существующие отклонения их абсолютными значениями или их квадратами. Так и поступают. Правда, в случае, когда возможные отклонения заменяют их абсолютными значениями, приходится оперировать с абсолютными величинами, что иногда приводит к серьезным затруднениям. Поэтому чаще всего идут по другому пути, т.е. вычисляют среднее значение квадрата отклонения, которое и называется дисперсией.
Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
.
В нашем случае = 30,1964 , = 269,5502.
Средним квадратическим отклонением случайной величины Х называют квадратный корень из дисперсии:
.
=5,495125, =16,41798.
Исправленная дисперсия :
S(x) = 30,50141, S(y) = 272,2729.
Выборочное исправленное среднее квадратическое отклонение:
= 5,522808, = 16,50069.
Часто статистические данные дополняются графиками. Графики являются самой эффективной формой представления данных с точки зрения их восприятия. Статистические графики представляют собой условные изображения числовых величин и их соотношений посредством линий, геометрических фигур, рисунков или географических карт-схем. Таким образом, облегчается рассмотрение статистических данных, они становятся наглядными, выразительными, обозримыми.
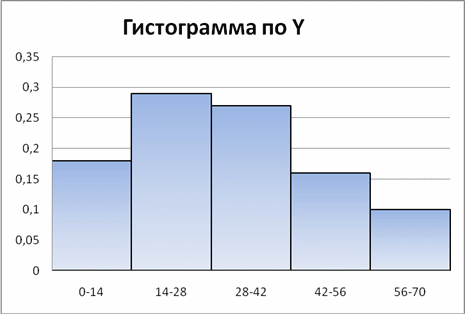
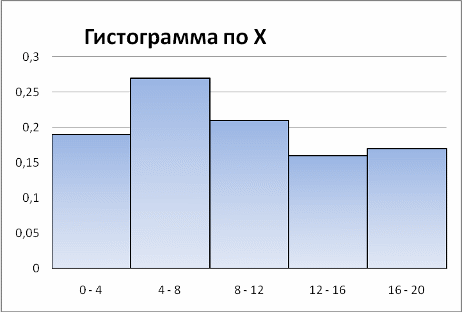
Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны частоте .
Гистограммой относительных частот называется диаграмма, на которой изображены столбцы, при этом ось Х — это интервалы, а ось У — это относительная частота встречаемости:
.
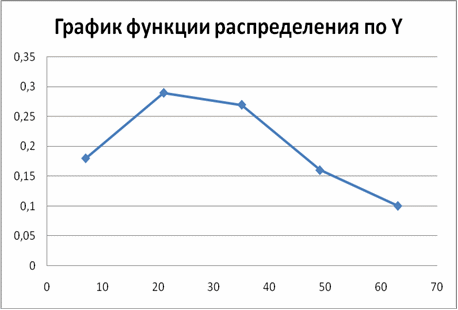
Полигоном частот называют ломаную, отрезки которой соединяют точки . Для построения полигона на оси абсцисс откладывают варианты , а на оси ординат соответствующие им частоты .
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки . Для построения полигона на оси абсцисс откладывают варианты , а на оси ординат соответствующие им относительные частоты .
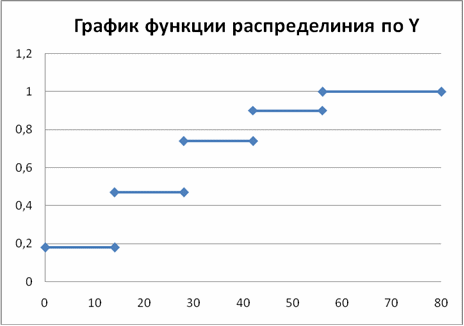
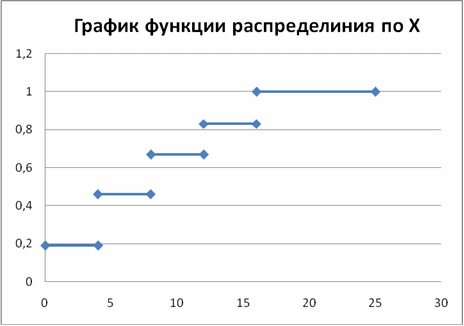
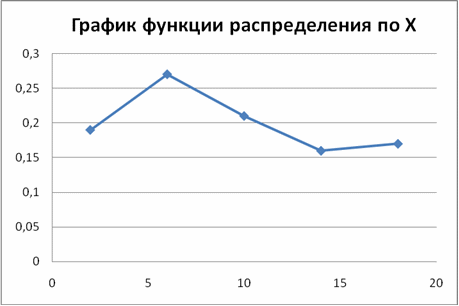
Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значения относительную частоту события . По определению , где — число вариант, меньших ; n — объем выборки. Функция обладает теми же свойствами, что и вероятность.
Нормальное распределение — приближённая плотность вероятности.
Плотность нормального распределения имеет вид:
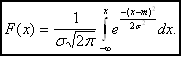
а функция распределения
.
Исходные данные и их обработка
Дана выборка (объема n=100), зависимости числа Y от числа X.
X
Y
X
Y
15
49,4
8,98
30,5
0,212
5,46
10,6
34,5
17,9
57,2
16,8
53,3
7,68
26,9
2,7
11,6
18
56,5
7,58
25,9
14,9
48
12,3
40,4
13,4
43,3
4,06
16,5
0,358
4
0,244
5,02
0,994
7,23
4,86
17,7
9,78
31,2
9,48
31,4
5
18,3
15,7
50,9
6,68
24,1
13,5
41,8
17,7
57,3
16,6
52,7
1,99
8,87
12,1
38,6
19,7
61,4
15
49,6
7,16
23,9
12,2
41,2
10,8
37,1
8,06
28,1
0,652
6,42
17,6
56,4
9,72
32,4
19,7
62,7
12,6
40,1
9,98
34
4,78
15,9
16,4
50,9
1,36
7,43
17,8
54,7
4,94
17,2
5,42
17,4
12,3
38,8
6,98
22,4
4,64
17,4
5,98
19
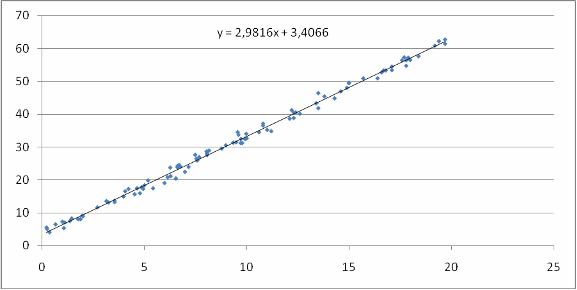
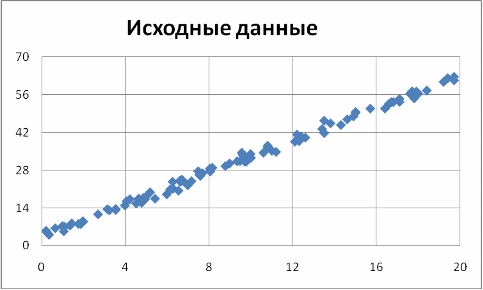
Начнем изучение данных X и Y с построения диаграммы рассеивания:
Диаграмма рассеивания наглядно показывает тенденцию возрастания Y при возрастании Х. Это объясняется тем, что при увеличении количества рабочих дней, зарплата возрастает.
Теперь построим корреляционную таблицу. Разобьём значения x на 5 и y на 5 интервалов:
y\x
2
6
10
14
18
N(y)
P*(y)
7
18
0
0
0
0
18
0,18
21
1
27
1
0
0
29
0,29
35
0
0
20
7
0
27
0,27
49
0
0
0
9
7
16
0,16
63
0
0
0
0
10
10
0,1
N(x)
19
27
21
16
17
100
P*(x)
0,19
0,27
0,21
0,16
0,17
1
По корреляционной таблице найдём оценки для Х:
выборочное среднее —, где :
=9,4;
выборочную дисперсию — :
=29,56;
исправленную дисперсию — :
=36,95;
среднеквадратичное отклонение — :
=5,436911;
оценку среднеквадратичного отклонения — :
=6,078651.
Найдем те же оценки для Y:
выборочное среднее —, где :
= 30,94;
выборочную дисперсию — :
= 291,2364;
исправленную дисперсию — :
=364,0455;
среднеквадратичное отклонение — :
=17,06565;
оценку среднеквадратичного отклонения — :
=19,07998.
и ковариацию и коэффициент кореляции для x, y:
,
, .
Точечной называют статистическую оценку, которая определяется одним числом , где – результаты n наблюдений над количественным признаком Х (выборка).
Несмещенной называют точечную оценку , математическое ожидание которой равно оцениваемому параметру при любом объеме выборки .
Оценки , , , , , — несмещённые оценки математического ожидания, дисперсии и среднеквадратичного отклонения.
Найдем также моду и медиану для Х и Y:
Модой дискретной случайной величины называется значение случайной величины, которое имеет максимальную вероятность:
= 15 , = 17,4.
Медиана — это такое значение варьирующего признака, которое приходится на середину упорядоченного ряда:
= 8,47, = 29,2.
Имея эти данные, можно построить гистограмму, полигон частот и функцию распределения для X, так же построим гистограмму, полигон частот и функцию распределения для Y.
Метод наименьших квадратов
Обычно в любой области науки при изучении двух величин проводятся эксперименты. Из-за того, что почти всегда измерение связано с погрешностями, соответствующие точки X и Y не ложатся на какую-то функцию и задача состоит в том, чтобы на основании экспериментальных точек выявить функциональную зависимость.
Если мы рассматриваем слабоформализованные системы, которые трудно поддаются однозначным и точным описаниям, связь между величинами X и Y изначально корреляционная. Это связано, в частности, с тем, что связи многопеременные, т.е. Y зависит не только от X, но и от других параметров, причем такая связь часто носит случайный характер.
В этом случае, имея экспериментальные точки, задача состоит в том, чтобы приближённо свести корреляционную связь к функциональной с помощью подбора такой функции, которая максимально возможным способом близка к экспериментальным точкам. Такая функция называется функцией регрессии.
Обычно вид самой функции угадывается, но она зависит от некоторых параметров. Задача статистического и корреляционного анализа состоит в нахождении этих параметров. Для этого и используется метод наименьших квадратов.
Линейная регрессия
Регрессия называется линейной, так как предполагается, что между X и Y существует линейная зависимость, то есть . Нужно провести эту прямую между экспериментальными точками оптимально. Введем некоторую величину – отклонение. Каждому x соответствуют два значения y. Пусть – экспериментальные точки, а – точки, соответсвующие значениям на прямой . Тогда пусть – расстояния между этимим точками. Отрезки – отклонения экспериментальных точек от теоретических. Отклонения разного знака, поэтому, чтобы полнее охарактеризовать суммарное отклонение, сложим их, возведя каждое в квадрат. Получим некоторую величину :
.
Очевидно, что линия регрессии будет оптимальной, если – суммарное отклонение в квадрате – минимальна. Для того, чтобы приняла минимальное значение, необходимо и достаточно, чтобы частные производные по и были равны нулю, т. е.
Решая систему, получим :
Решая систему, получим значения для a и b:
Пользуясь этими формулами мы сможем легко посчитать a, b и построить график линейной регрессии. В нашем случае a=2,9816, а b=3,4066. т. е. искомое уравнение линейной регрессии имеет вид y = 2,9816x + 3,4066. Для удобства наблюдения график регрессии будет на фоне диаграммы рассеивания.
Параболическая регрессия
Линейные связи являются основными, но нередко встречаются и нелинейные связи, хорошо описываемые параболой, гиперболой и т. д.
Уравнение регрессии в форме параболы второго порядка имеет вид: . Суммарное отклонение зависит от коэффициентов , и этой функции. Как и в предыдущем исследовании, нам необходимо провести оптимальную кривую, т. е. найти минимум функции .
Известно, что минимум достигается в точках, где частные производные равны нулю. В нашем случае имеем:
;
;
Решая систему, получаем a = 0,0002; b = 2,9769; c = 3,4225;
следовательно, искомое уравнение параболической регрессии имеет вид
математический систематизация квадратический отклонение
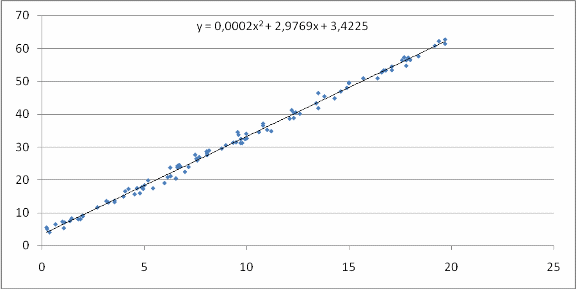
y = 0,0002x2 +2,9769x + 3,4225
Построим график параболической регрессии:
Сравним качество линейной и параболической регрессии по суммарному отклонению в квадрате.
Посчитаем искомое значение отклонений для регрессий
для линейной регрессии 110,4808;
для параболической регрессии 110,4797418,
где , – экспериментальные значения, а – теоретическое значение функции для .
Величина больше у линейной регрессии, и, следовательно, вместо линейной регрессии в данном случае лучше использовать параболическую.
Теперь мы подтвердили на практике, что чем больше степень уравнения регрессии, тем точнее график. Это легко заметить на рисунках. Но трудность вычислений сильно возрастает по мере возрастания степени уравнений. Однако наметилась интересная закономерность, в уравнениях регрессий, по мере возрастания степени уравнений n, коэффициенты перед переменными в этой степени стремятся к нулю. Это позволяет сделать вывод, что построение регрессий высших степеней не дало бы нам ощутимого улучшения результата.
Вывод
В курсовой работе был проведён статистический анализ Зависимость высоты дерева от среднегодовой температуры. Были получены основные параметры данной выборки. Также были приведены различные типы графиков: диаграмма рассеивания, гистограмма, полигон частот и функция распределения. На диаграмме рассеивания наглядно была показана прямая зависимость зарплаты от количества рабочих дней в год. Нами были получены знания о методах исследования математической статистики.
Список используемой литературы
1) Гмурман В.Е. Теория вероятностей и математическая статистика. — М.: Высшая школа, 1998.
2) Кабанова Е.И. «Теория вероятностей и математическая статистика».–Дубна: Кафедра ВМ и САУ, 1996.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ