Санкт-Петербургский Государственный Университет

Факультет прикладной математики – процессов управления

Кафедра диагностики функциональных систем

Анализ зависимости между УК в крови больных СКВ и степенью тяжести поражения почек

Курсовая работа

Варламова

Александра

Александровна

Научный руководитель

доктор медицинских наук, профессор Шишкин В.И.

Санкт-Петербург 2008

Содержание

§1. Введение

§2. Постановка задачи

§3. Используемые методы

1. Дисперсионный анализ по одному признаку для проверки равенства нескольких средних

2. Непараметрический дисперсионный анализ по одному признаку с применением критерия Краскала-Уоллиса для нескольких независимых выборок

3. Непараметрический дисперсионный анализ по одному признаку с применением критерия Джонкхиера для нескольких выборок, упорядоченных по возрастанию влияния фактора

§4.Вывод

§5. Список литературы

§1. Введение

Формулировка проблемы

Изложим проблемную ситуацию, имеющую место в настоящее время в решении задач обработки результатов исследований. Известно, что в распоряжении исследователей имеется большая и постоянно растущая в объеме база данных результатов измерений из разных областей естествознания: астрономии, экспериментальной физики, экономики, биологии, медицины.

По мнению автора, сформировавшемуся вследствии ознакомления с содержанием официальных высказываний ведущих политиков и ученых мира, наибольшего развития в 21 веке среди других наук достигнут биология и медицина. Известно и напечатано, например, в книге Е.В. Гублера "Информатика в патологии, клинической медицине и педиатрии" [1] , что в этом аспекте решение задач обработки результатов измерений приобретает ключевое значение . Следуя рекомендациям пособия "Кандидатская диссертация" [2] выполним критический анализ ситуации, сложившейся в настоящее время в России в решении задач обработки результатов наблюдений. Уже на предварительном этапе исследования имеет место противоречивая ситуация: с одной стороны – обработка найденных в медицине результатов измерений является актуальной задачей в современной науке, с другой стороны – известно, что в медицинских ВУЗах математика, как дисциплина учебного процесса , практически не изучается. Следовательно, то что методы обработки данных медицинских исследований стали предоставляться математикам-специалистам, создает прецедент выдвижения медицины в число приоритетных направлений Российской науки.

Изложив проблемную ситуацию, перейдем к определению цели и объекта исследования.

§2. Постановка задачи

Предварительные замечания

Системные заболевания соединительной ткани, такие как системная красная волчанка , характеризуются прежде всего выраженной патологией по иммунологической компоненте. Мониторинг этого контингента больных позволяет отнести системные заболевания к числу крайне тяжелых недугов, поражающих людей в наиболее деятельный возрастной период ( в среднем 30-50 лет )[8] и приводящих к ранней инвалидизации, а порой и к летальным исходам. Усиливающееся год от года неблагоприятное воздействие окружающей среды приводит к росту иммунодефицитов различной этиологии, в том числе возрастает заболеваемость системными вариантами иммунокомплексных патологий.

В иммунокомплексных патологиях система комплемента играет важную, хотя и не всегда ясную, роль. Таким образом изучение динамики комплемента приобретает ключевое теоретическое и практическое значение. В связи с этим нами предпринят анализ зависимости уровня комплемента с тяжестью течения классического иммунокомплексного заболевания системной красной волчанкой.

Объект, предмет, цель и задача исследования

В качестве исходных данных для исследования даны выборки численных значений медико-биологических показателей человеческого организма, а именно: уровня комплемента в крови больных системной красной волчанкой ( в дальнейшем – СКВ) и степенью тяжести поражения почек. . В целях полноты изложения приведем необходимое определение : "Комплемент - система сывороточных белков, которая активируется комплексом антиген - антитело с образованием биологически-активных веществ, способных вызывать необратимые повреждения клеточных мембран. Комплемент является одним из факторов естественного иммунитета и широко применяется в диагностических иммунологических реакциях."[3, ст. 57]

Объектом нашего исследования являлись выборочные данные результатов измерений уровня комплемента ( в дальнейшем - УК), причем изучаемые данные представляют собой пять столбцов чисел ,в первом из которых представлены данные без нефрита, во втором с нефритом слабовыраженным, в третьем с нефритом средней выраженности, в четвертом с нефротическим синдром, а в пятом- с почечной недостаточностью.

Предмет исследования определяем, как нахождение зависимости УК в крови больных СКВ и степенью тяжести поражения почек.

§3. Используемые методы

Будем использовать методы биометрического анализа, основанные на проверке гипотез однородности выборок.[9]

1. Дисперсионный анализ по одному признаку для проверки равенства нескольких средних

Во многих случаях практики интерес представляет вопрос о том, в какой мере существенно влияние того или иного фактора на рассматриваемый признак [9]. В данном случае фактором является степень поражения почек, а признаком - УК.

Научное обоснованное решение подобной задачи при некоторых предположениях составляет предмет дисперсионного анализа , введенного математиком- статистиком Р. А. Фишером.[10]

Статистическая модель

Выборки производятся из нормальных совокупностей. Первая выборка производиться из совокупности со средним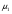, вторая - со средним 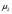, k-я из совокупности со средним 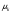. Все наблюдения независимы. Будем считать распределение данной мне совокупности нормальным.

Гипотезы №1.

Н₀ : = =…=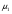

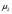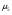
Н₁: не все средние равны. все средние равны.

Критическая область.

Верхняя 5%-ная область F_k-1.N-k -распределения. В нашем случае F_4,474 -распределения, так как k=4, а 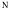=n₁ + n₂ + n₃ + n₄ + n₅ =479. Эта область определяется неравенством F2.37. ( Определяется по таблице, см. Таблица А.4а на стр. 334 "Справочника по вычислительным методам статистики" Дж. Поллард [6] )

Вычисление значения критериальной статистики

Будем рассматривать исходные данные, представленные Таблицей №1.

Таблица №1. Значения УК в зависимости от тяжести ГН.

.Нет нефрита

Выборка объема

n₁= 210

Слабый нефрит

Выборка объема n₂= 101

Средний нефрит

Выборка объема n₃= 98

Нефротический синдром

Выборка объема

n₄ = 45

Почечная недостаточность

Выборка объема

n₅ = 25

36

11

7

10

20

38

35

27

5

20

40

37

6

6

21

31

15

5

15

24

33

40

40

20

3

33,8

0

5

25

12

37

33

45

28

10

38

33

45

32

0

33

5

46

46

18,2

37

40

45

33

46

48

25

24

44

10

40

33

24

25

0

42

50

43

22,5

20

35

25

24,5

24,5

30,4

15

20

20,5

38

0

35

50

9

12

33,3

48

50

12

54,7

14,7

45

18

32

20,7

34,1

38

20

43

0

22,4

15

33

35,5

26,1

17,8

13

43

44

11

33,5

40

10

50

11,7

29,6

40

12

34

34,4

13,6

38

23

12

0

35

32,7

34

0

0

37

60

30

25,1

42

50

35

22,5

32,3

51

22

31

16

45

22,2

33

32,5

25

20

41,9

39,3

33

21

41,7

40,2

33

22

37,1

0

39

10

33,4

39,1

35,8

37,4

33

37,7

41,7

22,4

34,3

33,5

38,2

35

33

43,8

37,4

37,3

36,9

16

10

39,6

41

16

37,9

0

33

31

39,3

32,8

32,15

52

37,2

24

38,8

51

37,8

25

48,1

33,5

49,1

38

0

48

36,15

29

0

27

43,8

32

26,6

48

40

32

52,8

40

20

27

36

32,3

13,6

45

10

10

43,5

33,9

19,5

35

45,74

51,2

35

0

40,4

19,5

49,1

46,05

24,2

38

0

33

0

25,2

40,4

43,5

28

30

32,3

27

36

41

35

10

40

29

25

29,7

50

30

30

20

32

27,6

0

31

21,4

15,6

45

23

35

20

34,3

0

45

18

46

15

50,4

59,2

30,4

48,2

0

50

37,3

22,5

46

35

0

35

25

24

15

20

45

18

38

28,9

28

47,5

30,5

36,7

37,9

45,5

47,8

40,3

43

39,2

60

34,7

36,5

34,1

32,6

32

46,7

38,4

45,7

39

37,15

46,9

31,4

39

15,6

32

52,15

34,1

42

52,2

44,7

43,8

0

26,5

39,1

0

36,6

16

0

30,3

26,5

33

47

43

43

50

36,9

46,6

52,2

29,4

59,3

38,5

30,6

0

41

35,6

15,5

40

38,7

21,2

45

38,2

22,8

25,5

26,1

28,3

27,7

43,2

28,15

22,5

46

38,5

45

35,6

26

33

32,4

48,3

50

47,5

50

32

50

35,6

33,5

56,9

28,9

40

35,2

42,5

50

46,2

52,7

49,1

38

33,7

32,6

30

28,9

44,4

48,2

38,15

42

28,4

33,5

39,4

38,6

34,3

37,7

27,3

39,2

29,2

39,2

33,5

18

31,2

23,4

36,9

57,3

45

45,3

16,5

34,9

43,1

30,8

0

34,5

28

16

28,9

23

27

41,6

43,4

36

49

25

41,5

35,5

35

33,1

41,7

39,15

30,8

45,7

35,4

35,8

27

19,5

29,4

33,3

36,6

42,6

30

36,1

43

33,3

28,7

28,7

45,1

31,8

33

39,1

29

46,7

41,05

29,9

50

47

34,4

11

20,6

36,6

38,6

29,48

25

0

38

34,7

38,2

43,8

40,3

38,5

60

50

36

55

33,5

25,1

24,8

Всего:Т₁=7502,38

Т₂=3157,44

Т₃=2819,55

Т₄=1223,50

Т₅=505,60

Т = Т₁ + Т₂ + Т₃ + Т₄ + Т₅

Т=15208,47, Т² = 231297559,74, N = 479

Средние значения выборок:

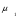=35,6

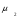= 31,1

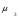= 28,7

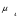= 26,38

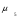= 19,8

Возведем в квадрат значение всех наблюдений и просуммируем их [6].

Вычисляем:

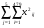=567988,11

Общая сумма квадратов будет следующей:

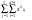- /N = 85112,2

Находим сумму квадратов между выборками:

(/n₁ +….+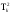/n_k ) – T²/N = 8470,35

Теперь можно заполнить таблицу дисперсионного анализа [6].

Таблица №2. Дисперсионный анализ по одному признаку.

Компонента дисперсии

(1)

Сумма квадратов

(2)

Степень свободы

(3)

Средний квадрат

(4)=(2)/(3)

Между выборками

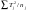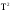()-/N

k-1

(определяется делением)

Остаточная

(определяется вычитанием)

N-k

Полная

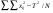
N-1

-----

Получаем:

Таблица №2а. Дисперсионный анализ по одному признаку. Результаты.

Компонента дисперсии

(1)

Сумма квадратов

(2)

Степень свободы

(3)

Средний квадрат

(4)=(2)/(3)

Между выборками

8470,35

4

2117,59

Остаточная

76641,85

474

161,69

Полная

85112,2

478

-----

Значение критериальной статистики равно:

F = средний квадрат между выборками / остаточный средний квадрат = 2117,59 / 161,69 = 13,09

Сравним F и F_критич : 13,092,37

Вывод. Следовательно, мы отвергаем гипотезу Н₀ ,то есть можно предположить, что при 5%-ном уровне значимости УК в крови больных СКВ зависит от степени тяжести поражения почек.

Мы не знаем, какое распределение имеют наши выборки. Описанный метод применяется , как это было описано в статистической модели, для нормальных совокупностей. В связи с этим будет правомочно применить непараметрический метод для выяснения равенства нескольких средних.

2. Непараметрический дисперсионный анализ по одному признаку с применением критерия Краскала-Уоллиса для нескольких независимых выборок

Для проверки совпадений нескольких средних часто применяется непараметрический критерий, свободный от распределения. Его можно использовать, когда рассматриваемые совокупности не являются нормально распределенными [7].

Статистическая модель

Имеется k совокупностей, в нашем случае 5 совокупностей. Каждая выборка извлекается из своей совокупности. Все наблюдения независимы.

Гипотезы

Н₀ : все k совокупностей одинаково распределены.

Н₁ : нулевая гипотеза не верна.

Критическая область

Верхняя 5%-ная область распределения 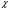²_k-1. В нашем случае 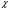²₄ , что соответствует значению критерия , превышающему 9,49. Данное число взято из Таблицы А.2 на стр. 331 "Справочника по вычислительным методам статистики" Дж. Полларда. [6]

Вычисление значения критериальной статистики

Для этого наблюдения x_ij заменяются их рангами r_ij .Все n наблюдений упорядоченны по возрастанию от 1 до n. Находим сумму рангов R₁, R₂,…, R_k для k групп. Вычисляем критерий [4]:

H= 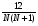( R²₁/n₁ +….+ R²_k/n_k ) – 3 ( N + 1 )

Значения комплемента упорядочены по возрастанию. Они иногда совпадают, тогда ранг принимает среднее значение.

Далее, используя Таблицу №1, присваиваем каждому значению комплемента соответствующий ранг в данных пяти выборках и получаем сумму рангов [5] .

Таблица №3. Таблица рангов наблюдений.

Нет

нефрита

Выборка объема n₁ = 210

Слабый

нефрит

Выборка объема

n₂ = 101

Средний

нефрит

Выборка объема

n₃ = 98

Нефротический синдром

Выборка объема

n₄ = 45

Почечная недостаточность

Выборка объема

n₅ = 25

УК

Ранг

УК

Ранг

УК

Ранг

УК

Ранг

УК

Ранг

36

282

11

45

7

33

10

39

20

86

38

315,5

35

264

27

144,5

5

28,5

20

86

40

352,5

37

296,5

6

31,5

6

31,5

21

95,5

31

188,5

15

59,5

5

28,5

15

59,5

24

115

33

220

40

352,5

40

352,5

20

86

3

26

33,8

242

0

13

5

28,5

25

126,5

12

50

37

296,5

33

220

45

405,5

28

28

10

39

38

315,5

33

220

45

405,5

32

197,5

0

13

33

220

5

28,5

46

420,5

46

420,5

18,2

77

37

296,5

40

352,5

45

405,5

33

220

46

420,5

48

436,5

25

126,5

24

115

44

396,5

10

39

40

352,5

33

220

24

115

25

126,5

0

13

42

375,5

50

453,5

43

383

22,5

105,5

20

86

35

264

25

126,5

24,5

119,5

24,5

119,5

30,4

181,5

15

59,5

20

86

20,5

92

38

315,5

0

13

35

264

50

453,5

9

34

12

50

33,3

231

48

436,5

50

453,5

12

50

54,7

471

14,7

56

45

405,5

18

74,5

32

197,5

20,7

94

34,1

247

38

315,5

20

86

43

383

0

13

22,4

102,5

15

59,5

33

220

35,5

273,5

26,1

137,5

17,8

72

13

53

43

383

44

396,5

11

45

33,5

237

40

352,5

10

39

50

453,5

11,7

47

29,6

171

40

352,5

12

50

34

244,5

34,4

252,5

13,6

54,5

38

315,5

23

110

12

50

0

13

35

264

32,7

210

34

244,5

0

13

0

13

37

296,5

60

478

30

176,5

25,1

132,5

42

375,5

50

453,5

35

264

22,5

105,5

32,3

204

51

462,5

22

99,5

31

188,5

16

68

45

405,5

22,2

101

33

220

32,5

207

25

26,5

20

86

41,9

373

39,3

345,5

33

220

21

95,5

41,7

371

40,2

359

33

220

22

99,5

37,1

299

0

13

39

334

10

39

33,4

233

39,1

337

35,8

278,5

37,4

304,5

33

220

37,7

306,5

41,7

371

22,4

102,5

34,3

250

33,5

237

38,2

323

35

264

33

220

43,8

393,5

37,4

304,5

37,3

302,5

36,9

293

16

68

10

39

39,6

346

41

365

16

68

37,9

309,5

0

13

33

220

31

188,5

39,3

343,5

32,8

211

32,15

202

52

465

37,2

301

24

115

38,8

332

51

462,5

37,8

308

25

126,5

48,1

439

33,5

237

49,1

445

38

315,5

0

13

48

436,5

36,15

286

29

165

0

13

27

144,5

43,8

393,5

32

197,5

26,6

141

48

436,5

40

352,5

32

197,5

52,8

470

40

352,5

20

86

27

144,5

36

282

32,3

204

13,6

54,5

45

405,5

10

39

10

39

43,5

390,5

33,9

243

19,5

79

35

264

45,74

417

51,2

464

35

264

0

13

40,4

362,5

19,5

79

49,1

445

46,05

424

24,2

118

38

315,5

0

13

33

220

0

13

25,2

134

40,4

362,5

43,5

390,5

28

152,5

30

176,5

32,3

204

27

144,5

36

282

41

365

35

264

10

39

40

352,5

29

165

25

126,5

29,7

172

50

453,5

30

176,5

30

176,5

20

86

32

197,5

27,6

149

0

13

31

188,5

21,4

98

15,6

64,5

45

405,5

23

110

35

264

20

86

34,3

250

0

13

45

405,5

18

74,5

46

425

15

59,5

50,4

461

59,2

475

30,4

181,5

48,2

440,5

0

13

50

453,5

37,3

302,5

22,5

105,5

46

420,5

35

264

0

13

35

264

25

126,5

24

115

15

59,5

20

86

45

405,5

18

74,5

38

315,5

28,9

161,5

28

152,5

47,5

432,5

30,5

183

36,7

291

37,9

309,5

45,5

414

47,8

434

40,3

360,5

43

383

39,2

341

60

478

34,7

255,5

36,5

287

34,1

247

32,6

208,5

32

197,5

46,7

427,5

38,4

325

45,7

415,5

39

334

37,15

300

46,9

429

31,4

192

39

334

15,6

64,5

32

197,5

52,15

466

34,1

247

42

375,5

52,2

467,5

44,7

399

43,8

393,5

0

13

26,5

139,5

39,1

337

0

13

36,6

289

16

68

0

13

30,3

180

26,5

139,5

33

220

47

430,5

43

383

43

383

50

453,5

36,9

293

46,6

426

52,2

467,5

29,4

168,5

59,3

476

38,5

327

30,6

184

0

13

41

365

35,6

276

15,5

63

40

352,5

38,7

331

21,2

97

45

405,5

38,2

323

22,8

108

25,5

135

26,1

137,5

28,3

156

27,7

150

43,2

388

28,15

155

22,5

46

420,5

38,5

327

45

105,5

35,6

276

26

136

33

220

32,4

206

48,3

442

50

453,5

47,5

432,5

50

453,5

32

197,5

50

453,5

35,6

276

33,5

237

56,9

473

28,9

161,5

40

352,5

35,2

271

42,5

378

50

453,5

46,2

425

52,7

469

49,1

445

38

315,5

33,7

241

32,6

208,5

30

176,5

28,9

161,5

44,4

398

48,2

440,5

38,15

321

42

375,5

28,4

157

33,5

237

39,4

345

38,6

329,5

34,3

250

37,7

306,5

27,3

148

39,2

341

29,2

167

39,2

341

33,5

237

18

74,5

31,2

191

23,4

112

36,9

293

57,3

474

45

405,5

45,3

413

16,5

71

34,9

257

43,1

387

30,8

185,5

0

13

34,5

254

28

152,5

16

68

28,9

161,5

23

110

27

144,5

41,6

369

43,4

389

36

282

49

443

25

126,5

41,5

368

35,5

273,5

35

264

33,1

229

41,7

371

39,15

339

30,8

185,5

45,7

415,5

35,4

272

35,8

278,5

27

144,5

19,5

79

29,4

168,5

33,3

231

36,6

289

42,6

379

30

176,5

36,1

285

43

383

33,3

231

28,7

158,5

28,7

158,5

45,1

412

31,8

193

33

220

39,1

337

29

165

46,7

427,5

41,05

367

29,9

173

50

453,5

47

430,5

34,4

252,5

11

45

20,6

93

36,6

289

38,6

289

29,48

170

25

126,5

0

13

38

315,5

34,7

255,5

38,2

323

43,8

393,5

40,3

360,5

38,5

327

60

478

50

453,5

36

282

55

472

33,5

237

25,1

132,5

24,8

121

Всего:

R₁=

57877

R₂=

23298.5

R₃=

21259.5

R₄=

8789

R₅=

3072

N = 479

k = 5

R₁ = 57877

n₁ = 210

R₂ = 23298,5

n₂ = 101

R₃ = 21259,5

n₃ = 98

R₄ = 8789

n₄ = 45

R₅ = 3072

n₅ = 25

Теперь можно полученные суммы рангов подставить в формулу и получить значение критериальной статистики Краскела-Уоллиса [4] :

Н=23,03

Полученный результат не является незначимым, поэтому нельзя считать, что выборки извлечены из одинаково распределенных совокупностей и что средние значения совокупностей совпадают. Но этот вывод является приближенным, так как в нашей таблице есть много совпадающих значений. Для учета влияния связей можно воспользоваться модифицированной формой статистики Краскела-Уоллиса [4]:

Н^` =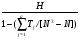

, где g – число групп совпадающих значений, Т_j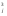 = (t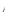 - t), t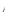– число совпадающих наблюдений в группе с номером j .

Таблица №4. Группы совпадающих наблюдений.

Повторяющиеся значения УК

Кол-во повторений t _j

Значение T_j

0

25

15600

5

4

60

6

2

6

10

9

720

11

3

24

12

5

120

13,6

2

6

15

6

210

15,6

2

6

16

5

120

18

4

60

19,5

3

24

20

11

1320

21

2

6

22

2

6

22,4

2

6

22,5

4

60

23

3

24

24

5

120

24,5

2

6

25

10

990

25,1

2

6

26,1

2

6

26,5

2

6

27

6

210

28

4

60

28,7

2

6

28,9

4

60

29

3

24

29,4

2

6

30

6

210

30,4

2

6

30,8

2

6

31

4

60

32

8

504

32,3

3

24

32,6

2

6

33

17

4896

33,3

3

24

33,5

7

336

34

2

6

34,1

3

24

34,3

3

24

34,4

2

6

34,7

2

6

35

13

2184

35,5

2

6

35,6

3

24

35,8

2

6

36

5

120

36,6

3

24

36,9

3

24

37

4

60

37,3

2

6

37,4

2

6

37,7

2

6

37,9

2

6

38

10

990

38,2

3

24

38,5

3

24

38,6

2

6

39

3

24

39,1

3

24

39,2

3

24

39,3

2

6

40

12

1716

40,3

2

6

40,4

2

6

41

3

24

41,7

3

24

42

4

60

43

7

336

43,5

2

6

43,8

4

60

44

2

6

45

12

1716

45,7

2

6

46

6

210

46,7

2

6

47

2

6

47,5

2

6

48

4

60

48,2

2

6

49,1

3

24

50

14

2730

51

2

6

52,2

2

6

60

3

24

g = 88

Теперь можно полученные результаты подставить в модифицированную формулу и получить уточненное значение критериальной статистики Краскела-Уоллиса :

Н^` = 23,037

Вывод. Скорректированное значение Н^` статистики Краскела-Уоллиса несущественно отличается от значения Н, т.о. мы можем отвергнуть гипотезу Н₀ на минимальном уровне значимости. Следовательно , мы подтвердили результат полученный ранее : существует зависимость между УК в крови больных СКВ и степенью тяжести поражения почек .

3. Непараметрический дисперсионный анализ по одному признаку с применением критерия Джонкхиера для нескольких выборок, упорядоченных по возрастанию влияния фактора

Нам заранее известно, что имеющиеся группы результатов упорядочены по возрастанию влияния фактора.. В нашем случае фактором является степень тяжести ГН. В таких случаях целесообразно использовать критерий Джонхиера , более чувствительный против альтернатив об упорядоченном влиянии фактора [5].

Статистическая модель

Имеется k совокупностей, в нашем случае 5 совокупностей. Каждая выборка извлекается из своей совокупности. Все наблюдения независимы. имеющиеся группы результатов упорядочены по возрастанию влияния фактора 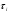. 1-й столбец Таблицы №1 отвечает наименьшему уровню фактора, последний – наибольшему, а промежуточные столбцы получили номера, соответствующие их положению. В нашем случае фактором является степень тяжести поражения почек [4] .

Гипотезы

Н₀ :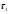==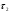…= 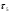( влияние фактора упорядоченно.)

Н₁ : …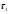

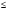
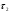
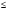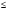
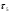
Критическая область

Верхняя 5% область F-распределения, что в нашем случае соответствует значению критерия, превышающему значение 2,21. Данное число взято из таблицы А.4 на стр. 334 [6].

Вычисление значения критериальной статистики

Вычислим статистику Манна – Уитни. Сравниваем k способов обработки, в нашем случае 5. Поступим следующим образом : для каждой пары натуральных чисел u и v , где 1 u  v  k , составляем по выборкам с номерами u,v статистику Манна – Уитни [4].

U = 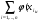, y)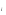

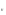Определим так же статистику Джонхиера как :

J =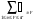

Для нахождения значений статистики Манна – Уитни будем использовать программу,( так как мы имеем выборки большого объема) написанную на языке Fortran Power Station для Windows , версия 4.0 .Выбор данного языка программирования связан с тем, что он максимально приближен к общепринятому языку математических формул. [11].

implicit real*8 (a-h, o-z)

dimension a1(210), a2(101),a3(98),a4(45),a5(25)

open (unit=11, file='1.dat', access='sequential', status='old')

open (unit=12, file='2.dat', access='sequential', status='old')

open (unit=13, file='3.dat', access='sequential', status='old')

open (unit=14, file='4.dat', access='sequential', status='old')

open (unit=15, file='5.dat', access='sequential', status='old')

open (unit=16, file='res.dat',access='append',status='unknown')

do 2222 i=1,210

read (11, 21) a1(i)

21 format(e8.1)

2222 continue

do 2223 i=1,101

read (12, 21) a2(i)

2223 continue

do 2224 i=1,98

read (13, 21) a3(i)

2224 continue

do 2225 i=1,45

read (14, 21) a4(i)

2225 continue

do 2226 i=1,25

read (15, 21) a5(i)

2226 continue

u12=0

do 101 i=1,210

do 91 j=1,101

if (a1(i)

u12 = u12+1

elseif (a1(i).eq.a2(j)) then

u12= u12+0.5

else

u12= u12+0.0

endif

91 continue

101 continue

u13=0

do 102 i=1,210

do 92 j=1,98

if (a1(i)

u13 = u13+1

elseif (a1(i).eq.a3(j)) then

u13= u13+0.5

else

u13= u13+0.0

endif

92 continue

102 continue

u14=0

do 103 i=1,210

do 93 j=1,45

if (a1(i)

u14 = u14+1

elseif (a1(i).eq.a4(j)) then

u14= u14+0.5

else

u14= u14+0.0

endif

93 continue

103 continue

u15=0

do 104 i=1,210

do 94 j=1,25

if (a1(i)

u15 = u15+1

elseif (a1(i).eq.a5(j)) then

u15= u15+0.5

else

u15= u15+0.0

endif

94 continue

104 continue

u23=0

do 105 i=1,101

do 95 j=1,98

if (a2(i)

u23 = u23+1

elseif (a2(i).eq.a3(j)) then

u23= u23+0.5

else

u23= u23+0.0

endif

95 continue

105 continue

u24=0

do 106 i=1,101

do 96 j=1,45

if (a2(i)

u24 = u24+1

elseif (a2(i).eq.a4(j)) then

u24= u24+0.5

else

u24= u24+0.0

endif

96 continue

106 continue

u25=0

do 107 i=1,101

do 97 j=1,25

if (a2(i)

u25 = u25+1

elseif (a2(i).eq.a5(j)) then

u25= u25+0.5

else

u25= u25+0.0

endif

97 continue

107 continue

u34=0

do 108 i=1,98

do 98 j=1,45

if (a3(i)

u34 = u34+1

elseif (a3(i).eq.a4(j)) then

u34= u34+0.5

else

u34= u34+0.0

endif

98 continue

108 continue

u35=0

do 109 i=1,98

do 99 j=1,25

if (a3(i)

u35 = u35+1

elseif (a3(i).eq.a5(j)) then

u35= u35+0.5

else

u35= u35+0.0

endif

99 continue

109 continue

u45=0

do 110 i=1,45

do 100 j=1,25

if (a4(i)

u45 = u45+1

elseif (a4(i).eq.a5(j)) then

u45= u45+0.5

else

u45= u45+0.0

endif

100 continue

110 continue

U=u12+u13+u14+u15+u23+u24+u25+u34+u35+u45

22 format(2x,'u12=',f10.3)

23 format(2x,'u13=',f10.3)

24 format(2x,'u14=',f10.3)

25 format(2x,'u15=',f10.3)

26 format(2x,'u23=',f10.3)

27 format(2x,'u24=',f10.3)

28 format(2x,'u25=',f10.3)

29 format(2x,'u34=',f10.3)

30 format(2x,'u35=',f10.3)

31 format(2x,'u45=',f10.3)

32 format(2x,'U=',f10.3)

write(16,22)u12

write(16,23)u13

write(16,24)u14

write(16,25)u15

write(16,26)u23

write(16,27)u24

write(16,28)u25

write(16,29)u34

write(16,30)u35

write(16,31)u45

write(16,32)U

end

Обработав таким образом результаты наблюдений, получаем значения статистики Манна – Уитни:

u12= 8441,000

u13= 7793,500

u14= 3172,500

u15= 888,000

u23= 4637,500

u24= 1928,500

u25= 648,500

u34= 2054,500

u35= 805,500

u45= 411,000

Подставив в формулу полученные значения получаем результат для статистики Джонхиера:

J= 30780,5

Значение статистики Джонхиера очень велико, что свидетельствует в пользу гипотезы Н₁ об упорядоченном влиянии фактора , в нашем случае – зависимости УК в крови больных СКВ от степени поражения почек. То есть мы снова подтвердили результат, полученный ранее.

Но поскольку предложенные выборки велики, то можно проверить полученный результат, подсчитав приближенную статистику J* для большой выборки [4].

Вычислим величину:

J^* = ( J – MJ ) /

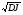
Где MJ = 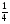( N² - 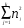) , DJ = 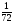( N² ( 2N + 3 ) - 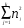( 2n_j + 3))

В результате вычислений мы получаем значение J^* = 5,9.

Вывод. Полученный результат превышает критическое значение, что позволяет отклонить гипотезу Н₀, и принять гипотезу Н_1. Таким образом мы подтверждается результат, полученный с помощью статистики J – влияние фактора в предложенных выборках упорядоченно.

§4. Вывод

Целью данной курсовой работы был анализ зависимости между УК в крови больных СКВ и степенью тяжести поражения почек. Исходные данные были подвергнуты методам статистического анализа, независимым между собой. Результатом является доказательство наличия зависимости УК в крови больных СКВ и степенью тяжести поражения почек в каждом из использованных методов, что позволяет сформулировать окончательный вывод : УК в крови больных СКВ зависит от степени тяжести поражения почек, причем УК уменьшается с возрастанием степени тяжести поражения почек.

§5. Список литературы

1. Гублер Е.В. Информатика в патологии, клинической медицине и педиатрии. –Л.: Медицина, 1990.-176с.

2. Кузин Ф.А. Кандидатская диссертация . Методика написания, правила оформления и порядок защиты. Практическое пособие для аспирантов и соискателей ученой степени. –5-е изд., доп.-М.:Ось 89, 2000.-224с.

3. Энциклопедический словарь медицинских терминов: В 3-х томах. Около 60000 терминов.-М.: Советская энциклопедия, - Т.2. 1983.-448с.

4. Тюрин Ю.Н. , Макаров А.А. Статистический анализ данных на компьютере .-М.: Инфра – М., 1982.-528с.

5. Холлендер М., Вулф Д.А. Непараметрические методы статистики.-М.: Финансы и статистика., 1983.-518с.

6. Поллард Дж. Справочник по вычислительным методам статистики.-М.: Финансы и статистика., 1982.-344с.

7. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Исследование зависимостей.-М.: Финансы и статистика,-Т.2. 1985.-488с.

8. Шишкин В.И., Кудрявцева Г.В. Регуляторная роль функциональной системы "Комплемент – простагландиды – пентозофосфатный путь обмена углеводов" в патогенезе основных ревматологических заболеваний.-СПб.: НИИХ. 2002.-38с.

9. Колмогоров А.Н. Теория вероятности и математическая статистика.-М.:Наука.,1986.-535с.

10. Фишер Р.А. Статистические методы для исследователей.-М.:Госстатиздат.,1982.-344с.

11. Фишер Ф.П., Суиндл Д.Ф. Системы программирования.-М.:Статистика.,1971.-606с.