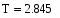
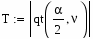
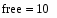
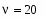
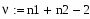
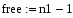
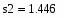
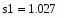
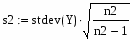
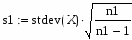
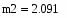
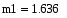
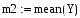
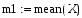
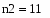
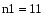
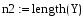
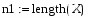
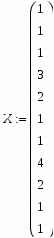
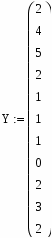
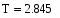
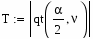
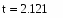
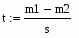
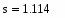
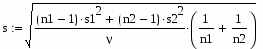
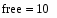
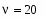
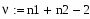
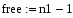
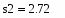
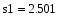
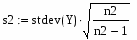
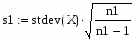
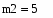
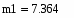
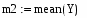
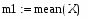
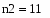
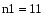
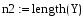
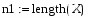
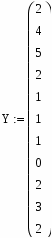
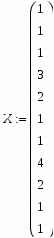
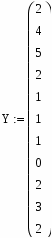
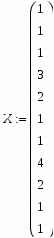
МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ УКРАИНЫ

ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

имени В.Н.Каразина

Факультет фундаментальной медицины

Кафедра общей и клинической иммунологии и

аллергологии

Курс социальной медицины, экономики и организиции

здравоохранения

КУРСОВАЯ РАБОТА

Организация и проведение медико-статистического исследования

"Определение эффективности введения предуктала в стандартную схему лечения пациентов ИБС, стенокардией"

Выполнил:

студент группы ВИ-52

Панов Станислав Игоревич

Проверил:

асс. Козлов Александр Петрович

Харьков

2007

Курсовая работа №29. В исследовании определялась эффективность стандартной антиангинальной терапии и такой же терапии с добавлением предуктала. По заявлению фармацевтической фирмы-производителя предуктал резко повышает эффективность и безопасность антиангинальной терапии. В нашем исследовании были обследованы 22 пациента с ИБС, стенокардией III ФК, которые были разделены на две группы (по 11 человек случайным образом). Пациенты первой группы получали стандартную терапию, 2 группы стандартную терапию с предукталом. Для оценки качества антиангинальной терапии использовали измеренную в баллах (10 баллов максимум) толерантность к физическим нагрузкам, а для оценки безопасности лечения – количество обращений к врачу за 6 месяцев наблюдения для коррекции терапии вследствие неэффективности или низкой эффективности ранее назначенной терапии. Получены следующие данные:

1 группа

2 группа

Толерантность к физ. нагрузкам,

баллы

Количество повторных обращений

Толерантность к физ. нагрузкам,

баллы

Количество повторных обращений

10

1

5

2

8

1

4

4

6

1

6

5

8

3

7

2

7

2

3

1

9

1

2

1

2

1

9

1

10

4

10

0

8

2

4

2

9

1

2

3

4

1

3

2

Цель исследования: определить эффективность введения предуктала в стандартную схему лечения пациентов ИБС, стенокардией, оценить эффективность предуктала в повышении толерантности к физическим нагрузкам и его эффективность в снижении количества повторных обращений вследствие неэффективности ранее назначенной терапии.

Этап I. Определение цели и составление программы исследования

Исследование будет проведено согласно стандартному плану медико–статистического исследования. В процессе исследования будет выяснена эффективность введения предуктала в стандартную схему лечения пациентов ИБС, стенокардией.

В процессе проведения первого этапа медико-статистического исследования сформулируем цель работы и определим программу медико-статистического исследования.

Цель работы: определить эффективность введения предуктала в стандартную схему лечения пациентов ИБС, стенокардией, оценить эффективность предуктала в повышении толерантности к физическим нагрузкам и его эффективность в снижении количества повторных обращений вследствие неэффективности ранее назначенной терапии.

Программа медико-статистического исследования:

• Программа сбора материала – данные о толерантности к физическим нагрузкам получаем после проведения велоэргометрии, оценку проводим в баллах(максимум 10 баллов); данные о количестве повторных обращений вследствие неэффективности ранее назначенной терапии получаем из журнала посещений больными ЛПУ.

• Программа разработки материала – в процессе разработки будет построена простая таблица; признаком эффективности будем считать толерантность к физическим нагрузкам, а признаком безопасности - количество повторных обращений вследствие неэффективности ранее назначенной терапии.

• Программа анализа материала – в процессе анализа данных, которые будут получены согласно программы сбора материалов, будет проведён дисперсионный анализ, в частности критерий Стьюдента, полученных данных и рассчитаны показатели эффективности и безопасности применения различных схем лечения пациентов ИБС, стенокардией, на основании которых будут сделаны выводы о наиболее эффективной и безопасной схеме лечения.

• План медико-статистического исследования: объектом наблюдения будут больные ИБС, стенокардией III ФК; будет использована выборочная, единовременная, репрезентативная, достаточная по объёму статистическая совокупность; сбор материала будет проведён методом получения данных после проведения велоэргометрической пробы, а так же методом копирования данных из журнала посещаемости ЛПУ; метод разработки материала – ручной; работа будет проведена в срок с 01.12.2007 по 31.12.2007 силами студента группы ВИ - 52 Панова Станислава Игоревича.

Этап II. Сбор материала для исследования

В процессе выполнения второго этапа медико-статистического исследования в соответствии с программой сбора материала был проведён анализ данных велоэргометрических проб, отражающих эффективность схемы лечения пациентов ИБС, стенокардией и частоте повторных обращений вследствие неэффективности ранее назначенной терапии, отражающей безопасность проводимой терапии.

Этап III. Статистическая разработка материала

В процессе выполнения программы сбора материала были получены нижеприведенные данные, которые буду представлены в виде простой таблицы

1 группа

2 группа

Толерантность к физ. нагрузкам,

баллы

Количество повторных обращений

Толерантность к физ. нагрузкам,

баллы

Количество повторных обращений

10

1

5

2

8

1

4

4

6

1

6

5

8

3

7

2

7

2

3

1

9

1

2

1

2

1

9

1

10

4

10

0

8

2

4

2

9

1

2

3

4

1

3

2

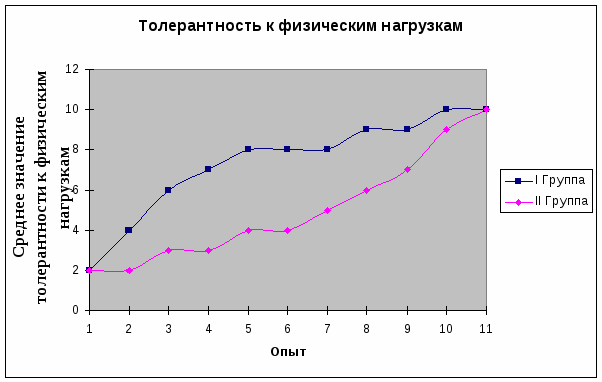
Для большей наглядности отобразим полученные данные графически. Для отображения такого типа данных наиболее рационально использовать линейную диаграмму. Сперва отобразим линейную диаграмму и проведём все необходимые расчёты по эффективности стандартной схемы лечения и схемы лечения с добавлением предуктала, а далее отобразим линейную диаграмму и проведём все необходимые расчёты по безопасности стандартной схемы лечения и схемы лечения с добавлением предуктала:

На графике заметна выраженная тенденция к повышению толерантности к физическим нагрузкам в группе, в которой проводилась стандартная терапия, по сравнению с группой в которой проводилась терапия с добавлением предуктала. График даёт косвенное доказательство того что стандартная схема лечения в большей мере повышает толерантность к физическим нагрузкам у больных ИБС, стенокардией.

Для определения наиболее эффективной схемы лечения больных ИБС, стенокардией необходимо рассчитать коэффициент Стьюдента, для этого будет использован пакет MS OFFICE EXCEL и программа MATHCAD.

Ход вычисления коэффициента Стьюдента:

1) Для вычисления коэффициента Стьюдента необходимо, что бы выборки имели нормальное распределение.

Условно обозначим пациентов получающих стандартную терапию "Группа I", а пациентов получающих терапию с добавлением предуктала "Группа II":

Входит в

Данные

3 сигма

1 сигма

0,625 сигма

10

0

1

1

-2,6364

48,308

8

0

0

1

-0,6364

0,164

6

0

0

0

1,36364

3,4578

8

0

0

1

-0,6364

0,164

7

0

0

1

0,36364

0,0175

9

0

0

1

-1,6364

7,17

2

0

1

1

5,36364

827,63

10

0

1

1

-2,6364

48,308

8

0

0

1

-0,6364

0,164

9

0

0

1

-1,6364

6561

4

0

1

0

3,36364

128,01

Количество испытаний -

11

Среднее значение выборки -

7,363636364

Среднее квадратичное отклонение -

2,500908926

Стандартная ошибка выборки -

0,754052413

Дисперсия выборки -

6,254545455

Лево

Право

Трехсигмовый интервал -

-0,139090413

14,86636314

Сигмовый интервал -

4,862727438

9,864545289

0,625-сигмовый интервал -

5,800568285

9,864545289

%

Результат:

Проверка условия а)

0

Распределение нормальное

 

Проверка условия б)

2,090909

Распределение нормальное

 

Проверка условия в)

2,636364

Распределение нормальное

 

Проверка данных, по толерантности к физическим нагрузкам в 1 группе, на соответствие нормальному закону распределения:

Известно следующее свойство нормального распределения:

а) почти все (99,7%) отклонения от среднего меньше 3-х сигм

б) две трети (68,3%) меньше чем сигма

в) половина отклонений меньше, чем 0,625 сигм

Проверка данных, по толерантности к физическим нагрузкам во 2 группе, на соответствие нормальному закону распределения:

Известно следующее свойство нормального распределения:

а) почти все (99,7%) отклонения от среднего меньше 3-х сигм

б) две трети (68,3%) меньше чем сигма

в) половина отклонений меньше, чем 0,625 сигм

Входит в

Данные

3 сигма

1 сигма

0,625 сигма

5

0

0

1

0

0

4

0

0

0

1

1

6

0

0

1

-1

1

7

0

0

1

-2

16

3

0

0

0

2

16

2

0

1

1

3

81

9

0

1

1

-4

256

10

0

1

1

-5

625

4

0

0

0

1

1

2

0

1

1

3

16

3

0

0

0

2

16

Количество испытаний -

11

Среднее значение выборки -

5

Среднее квадратичное отклонение -

2,720294102

Стандартная ошибка выборки -

0,820199532

Дисперсия выборки -

7,4

Лево

Право

Трехсигмовый интервал -

-3,160882305

13,16088231

Сигмовый интервал -

2,279705898

7,720294102

0,625-сигмовый интервал -

3,299816186

7,720294102

%

Результат:

Проверка условия а)

0

Распределение нормальное

 

Проверка условия б)

2,090909

Распределение нормальное

 

Проверка условия в)

2,454545

Распределение нормальное

 

Вывод: выборки имеют нормальный закон распределения.

2) Вычислим коэффициент Стьюдента с помощью MATHCAD:

1. Сформируем нулевую и альтернативную гипотезу: Н₀ Стандартная терапия эффективнее если полученное значение коэффициента меньше критического значения, а Н₁ Терапия с предукталом эффективнее если полученное значение коэффициента больше критического значения.

Где Х – это количество повторных обращений в 1 группе, а Y – это повторных обращений во 2 группе.

2. Зададимся уровнем значимости:

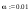
3. Определим количество выборок с помощью встроенной функции length(X,Y), в программе Mathcad:

4. Вычислим среднее значение выборок с помощью встроенной функции mean(X,Y), в программе Mathcad:

5. Определим средние квадратичные отклонения выборок:

где s1 – это среднее квадратичное отклонение 1 группы, а s2 - это среднее квадратичное отклонение 2 группы.

6. Вычислим количество степеней свободы:

7. Определим стандартную ошибку среднего по формуле:

8. Вычислим коэффициент Стьюдента по формуле:

9. Вычислим критическое значение коэффициента Стьюдента:

10. Нулевая гипотеза принимается, если |t|<T:

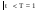
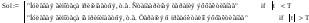
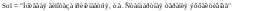
Вывод: Исходя из полученных результатов, можно, статистически достоверно, сказать, что стандартная терапия эффективнее терапии с добавлением предуктала.

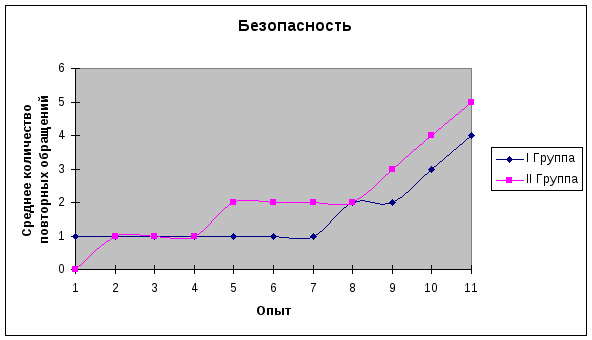
На графике заметна тенденция к повышению количества повторных посещений в группе, в которой проводилась терапия с добавлением предуктала, по сравнению с группой в которой проводилась стандартная терапия. График даёт косвенное доказательство того что стандартная схема лечения в большей мере безопасна чем терапия с предукталом.

Для определения наиболее безопасной схемы лечения больных ИБС, стенокардией необходимо рассчитать коэффициент Стьюдента, для этого будет использован пакет MS OFFICE EXCEL и программа MATHCAD.

Ход вычисления коэффициента Стьюдента:

1) Для вычисления коэффициента Стьюдента необходимо, что бы выборки имели нормальное распределение.

Условно обозначим пациентов получающих стандартную терапию "Группа I", а пациентов получающих терапию с добавлением предуктала "Группа II":

Проверка данных, по количеству повторных обращений в 1 группе, на соответствие нормальному закону распределения:

Известно следующее свойство нормального распределения:

а) почти все (99,7%) отклонения от среднего меньше 3-х сигм

б) две трети (68,3%) меньше чем сигма

Входит в

3 сигма

1 сигма

0,625 сигма

Безопасность

1 группа

1

0

0

0

0,63636

0,164

1

0

0

0

0,63636

0,164

1

0

0

0

0,63636

0,164

3

0

1

1

-1,3636

3,4578

2

0

0

1

-0,3636

0,0175

1

0

0

0

0,63636

0,164

1

0

0

0

0,63636

0,164

4

0

1

1

-2,3636

31,212

2

0

0

1

-0,3636

0,0175

1

0

0

0

0,63636

1

1

0

0

0

0,63636

0,164

Количество испытаний -

11

Среднее значение выборки -

1,636363636

Среднее квадратичное отклонение -

1,026910636

Стандартная ошибка выборки -

0,309625207

Дисперсия выборки -

1,054545455

Лево

Право

Трехсигмовый интервал -

-1,444368272

4,717095545

Сигмовый интервал -

0,609453

2,663274272

0,625-сигмовый интервал -

0,994544489

2,663274272

%

Результат:

Проверка условия а)

0

Распределение нормальное

 

Проверка условия б)

1,909091

Распределение нормальное

 

Проверка условия в)

2,181818

Распределение нормальное

 

в) половина отклонений меньше, чем 0,625 сигм

Проверка данных, по количеству повторных обращений во 2 группе, на соответствие нормальному закону распределения:

Известно следующее свойство нормального распределения:

а) почти все (99,7%) отклонения от среднего меньше 3-х сигм

б) две трети (68,3%) меньше чем сигма

в) половина отклонений меньше, чем 0,625 сигм

Входит в

3 сигма

1 сигма

0,625 сигма

Безопасность

2 группа

2

0

0

0

0,09091

7E-05

4

0

1

1

-1,9091

13,283

5

0

1

1

-2,9091

71,619

2

0

0

0

0,09091

7E-05

1

0

0

0

1,09091

1,4163

1

0

0

0

1,09091

1,4163

1

0

0

0

1,09091

1,4163

0

0

1

1

2,09091

19,114

2

0

0

0

0,09091

7E-05

3

0

0

1

-0,9091

81

2

0

0

0

0,09091

7E-05

Количество испытаний -

11

Среднее значение выборки -

2,090909091

Среднее квадратичное отклонение -

1,445997611

Стандартная ошибка выборки -

0,435984684

Дисперсия выборки -

2,090909091

Лево

Право

Трехсигмовый интервал -

-2,247083742

6,428901924

Сигмовый интервал -

0,64491148

3,536906702

0,625-сигмовый интервал -

1,187160584

3,536906702

%

Результат:

Проверка условия а)

0

Распределение нормальное

 

Проверка условия б)

2

Распределение нормальное

 

Проверка условия в)

2,181818

Распределение нормальное

 

Вывод: выборки имеют нормальный закон распределения.

3) Вычислим коэффициент Стьюдента с помощью MATHCAD:

Сформируем нулевую и альтернативную гипотезу: Н₀ Стандартная терапия безопаснее если полученное значение коэффициента меньше критического значения, а Н₁ Терапия с предукталом безопаснее если полученное значение коэффициента больше критического значения.

Где Х – это количество повторных обращений в 1 группе, а Y – это повторных обращений во 2 группе.

1.Зададимся уровнем значимости:

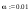
2.Определим количество выборок с помощью встроенной функции length(X,Y), в программе Mathcad:

3.Вычислим среднее значение выборок с помощью встроенной функции mean(X,Y), в программе Mathcad:

4.Определим средние квадратичные отклонения выборок:

где s1 – это среднее квадратичное отклонение 1 группы, а s2 - это среднее квадратичное отклонение 2 группы.

5.Вычислим количество степеней свободы:

6.Определим стандартную ошибку среднего по формуле:

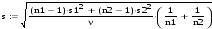
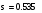
7.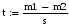Вычислим коэффициент Стьюдента по формуле:

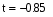
8.Вычислим критическое значение коэффициента Стьюдента:

9.Нулевая гипотеза принимается, если |t|<T:

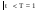
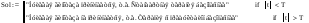
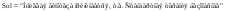
Вывод: Исходя из полученных результатов, можно, статистически достоверно, сказать, что стандартная терапия безопаснее терапии с добавлением предуктала.

Этап IV. Анализ полученных данных, выводы и рекомендации

В результате проведённого нами медико-статистического исследования, целью которого являлось изучение эффективности введения предуктала в стандартную схему лечения пациентов ИБС, стенокардией, оценивание эффективности предуктала в повышении толерантности к физическим нагрузкам и его эффективности в снижении количества повторных обращений вследствие неэффективности ранее назначенной терапии, нами получены статистически достоверные результаты (|t| < T).

В свою очередь, эти данные дают возможность говорить о том, что введение предуктала в стандартную схему лечения пациентов ИБС, стенокардией является неэффективным и менее безопасным по сравнению со стандартной схемой лечения.

Исходя из полученных нами данных, рекомендуется не применять стандартную схему лечения пациентов ИБС, стенокардией совместно с предукталом.