Оценка и анализ рисков 2
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Филиал государственного образовательного учреждения высшего профессионального образования
ВСЕРОССИЙСКОГО ЗАОЧНОГО
ФИНАНСОВО – ЭКОНОМИЧЕСКОГО ИНСТИТУТА
в г. Брянске
ЛАБОРАТОРНАЯ РАБОТА на ПЭВМ
по дисциплине
«ОЦЕНКА И АНАЛИЗ РИСКОВ»
-
ВЫПОЛНИЛ(А)
Мирошниченко Н. О.
СТУДЕНТ(КА)
6-го курса
СПЕЦИАЛЬНОСТЬ
Финансы и кредит (Финансовый менеджмент)
№ ЗАЧЕТНОЙ КНИЖКИ
05ФФБ 02518
ПРЕПОДАВАТЕЛЬ
Малашенко В.М.
Брянск — 2010
ВАРИАНТ 8
В таблице приведена информация по месячным доходностям за 2007 год:
Месяц
Доходности индексов за месяц (%)
RTS
RTSmm
RTSfn
январь 2007
-5,055
2,121
-1,511
февраль 2007
4,456
5,737
4,212
март 2007
1,555
1,915
9,241
апрель 2007
-0,011
2,080
2,595
май 2007
-8,018
3,039
-4,965
июнь 2007
6,593
7,145
4,553
июль 2007
5,072
12,003
3,406
август 2007
-3,715
4,415
-2,282
сентябрь 2007
7,912
-0,059
0,700
октябрь 2007
7,301
-0,251
5,521
ноябрь 2007
-0,133
2,529
0,778
декабрь 2007
3,171
12,414
4,491
Требуется:
Определить характеристики каждого отраслевого индекса: коэффициент смещения , коэффициент чувствительности , ры ночный (систематический) риск, собственный (несистематический) риск, коэффициент детерминации R2.
Сформировать портфель минимального риска из двух видов отраслевых индексов при условии, что обеспечивается доходность портфеля (mp) не менее, чем по безрисковым ценным бумагам (обли гациям) — 0,5 %, с учетом общего индекса рынка.
Построить линию рынка ценных бумаг (SML).
Построить линию рынка капитала (CML).
РЕШЕНИЕ
1. С помощью встроенных функций «ОТРЕЗОК» и «НАКЛОН» табличного процессора Excel определяем для каждого отраслевого индекса оценки коэффициентов смещения 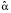 и чувствительности
и чувствительности 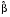 (приложение 1):
(приложение 1):
отраслевого индекса 1 (RTSmm):
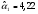 ;
; 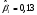 ;
;отраслевого индекса 2 (RTSfn):
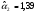 ;
; 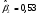 .
.
Уравнения регрессии рыночных моделей имеют вид:
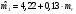 ;
;
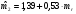 ,
,
где mr — доходность общего индекса рынка RTS (доходность рынка).
Коэффициенты смещения (-коэффициенты) показывают, что при нулевой доходности рынка средняя доходность индекса 1 составляет 4,22%, индекса 2 — (1,39) %.
Коэффициенты чувствительности (-коэффициенты) показывают, что при увеличении доходности рынка на 1 % доходность индекса 1 возрастает в среднем на 0,13 %, индекса 2 — в среднем на 0,53 %. Положительные значения коэффициентов свидетельствуют о том, что динамика доходности отраслевых индексов в целом соответствует динамике рынка. Изменение индекса 1 оказалось «агрессивнее» рынка, тогда как изменение индекса 2 является «оборонительным».
Линии регрессии доходности отраслевых индексов по общему индексу рынка показаны на графиках (см. приложения 2, 3).
Средняя доходность отраслевых индексов определяется с помощью встроенной функции «СРЗНАЧ» (см. приложение 1):
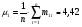 %;
%;
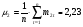 %.
%.
Общий риск (дисперсия доходности) отраслевых индексов рассчитывается с помощью встроенной функции «ДИСП» (см. приложение 1):
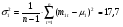 ;
;
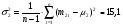 .
.
Общий риск отраслевого индекса 2 ниже, чем индекса 1.
Дисперсия доходности рынка также определяется с помощью функции «ДИСП» (см. приложение 1):
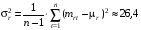 .
.
Определяем рыночный 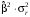 и собственный
и собственный 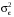 риски отраслевых индексов, а также коэффициенты детерминации R2 их доходностей по отношению к доходности рынка (см. также приложение 1):
риски отраслевых индексов, а также коэффициенты детерминации R2 их доходностей по отношению к доходности рынка (см. также приложение 1):
индекса 1:
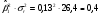 ;
;
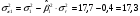 ;
;
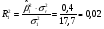 ;
;
индекса 2:
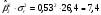 ;
;
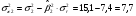 ;
;
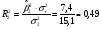 .
.
Коэффициенты детерминации R2 показывают, что поведение отраслевого индекса 1 на 2 % предсказуемо с помощью общего индекса рынка, поведение отраслевого индекса 2 предсказуемо на 49 %.
2. Если портфель ценных бумаг образуется из отраслевых индексов 1 и 2, то задача его формирования может быть представлена как задача нелинейного программирования:
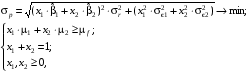
где 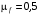 % — доходность безрисковых ценных бумаг (облигаций).
% — доходность безрисковых ценных бумаг (облигаций).
В числовом виде задача оптимизации имеет вид:
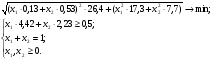
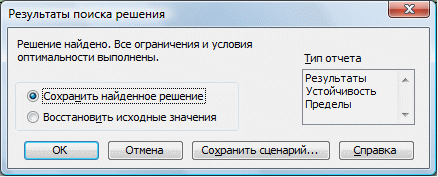
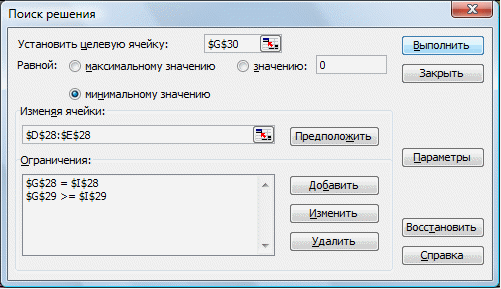
Для ее решения используется надстройка «Поиск решения» Excel (меню «Сервис» «Поиск решения…»):
После запуска надстройки на выполнение было получено оптимальное решение задачи: x1=0,535; x2=0,465 (см. приложение 1). Это означает, что при заданной нижней границе доходности 0,5 % наименьший риск портфеля будет достигнут, если доля отраслевого индекса 1 составит 53,5 %, а доля отраслевого индекса 2 — 46,5 %.
Оптимальный портфель имеет следующие характеристики (см. также приложение 1):
средняя доходность:
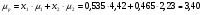 %;
%;
риск (стандартное отклонение):
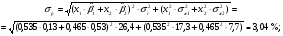
коэффициент чувствительности:
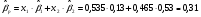 .
.
3. Уравнение линии рынка ценных бумаг (SML) имеет вид:
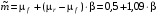 ,
,
где 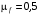 % — доходность безрисковых ценных бумаг (облигаций);
% — доходность безрисковых ценных бумаг (облигаций); 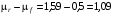 % — средняя рыночная премия за риск.
% — средняя рыночная премия за риск.
Ожидаемые доходности отраслевых индексов 1 и 2 при условии равновесия рынка соответственно равны:
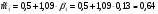 %;
%;
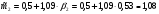 %;
%;
ожидаемая доходность портфеля —
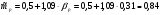 %.
%.
Линия SML изображена на графике (см. приложение 4), из которого видно, что отраслевой индекс 1 переоценен, а отраслевой индекс 2, наоборот, недооценен. Переоцененным является и сформированный портфель из этих индексов.
4. Уравнение линии рынка капитала (CML) имеет вид:
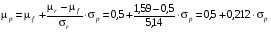 ,
,
где 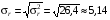 % — стандартное отклонение доходности рынка.
% — стандартное отклонение доходности рынка.
Линия CML изображена на графике (см. приложение 5), из которого видно, что средняя доходность сформированного портфеля превышает ожидаемую доходность эффективного портфеля для того же самого значения риска.
ПРИЛОЖЕНИЕ: компьютерные распечатки на 5 листах.

Нравится материал? Поддержи автора!
Ещё документы из категории менеджмент :
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ