Законы сохранения
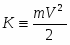
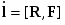
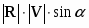
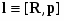
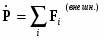
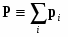
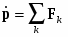
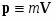 Законы сохранения
Законы сохранения
Иерархия естественно научных законов.
Количество законов природы, сформулированных в естественных науках к настоящему времени, весьма велико. Они неравнозначны.
Наиболее многочисленным является класс эмпирических законов, формулируемых в результате обобщения результатов экспериментальных наблюдений и измерений. Часто эти законы записываются в виде аналитических выражений, носящих достаточно простой, но приближенный характер. Область применимости этих законов оказывается достаточно узкой. При желании увеличить точность или расширить область применимости математические формулы, описывающие такие законы, существенно усложняются. Примерами эмпирических законов могут служить закон Гука (при небольших деформациях тел возникают силы, примерно пропорциональные величине деформации), закон валентности (в большинстве случаев атомы объединяются в химические соединения согласно их валентности, определяемым положением в Периодической таблице элементов), некоторые частные законы наследственности ( напр. сибирские коты с голубыми глазами обычно от рождения глухи). На ранних этапах развития естественных наук в основном шло по пути накопления подобных законов. Со временем их количество возросло настолько, что возник вопрос о нахождении новых законов, позволяющих описать эмпирические в более компактной форме.
Фундаментальные законы представляют собой весьма абстрактные формулировки, непосредственно не являющиеся следствием экспериментов. Обычно фундаментальные законы “угадываются”, а не выводятся из эмпирических. Количество таких законов весьма ограничено (напр. классическая механика содержит в себе лишь 4 фундаментальных закона: законы Ньютона и закон Всемирного тяготения). Многочисленные эмпирические законы являются следствиями (иногда вовсе не очевидными) фундаментальных. Критерием истинности последних является соответствие конкретных следствий экспериментальным наблюдениям. Все известные на сегодняшний день фундаментальные законы описываются достаточно простыми и изящными математическими выражениями, “не ухудшающимися” при уточнениях. Несмотря на кажущийся абсолютный характер, область применимости фундаментальных законов так же ограничена. Эта ограниченность не связана с математическими неточностями, а имеет более фундаментальный характер: при выходе из области применимости фундаментального законы начинают терять смысл сами понятия, используемые в формулировках (так для микрообъектов оказывается невозможным строгое определение понятий ускорения и силы, что ограничивает применимости законов Ньютона).
Ограниченность применимости фундаментальных законов естественно приводит к вопросу о существовании еще более общих законов. Таковыми являются законы сохранения. Имеющийся опыт развития естествознания показывает, что законы сохранения не теряют своего смысла при замене одной системы фундаментальных законов другой. Это свойство теперь используется как эвристический принцип, позволяющий априорно отбирать “жизнеспособные” фундаментальные законы при построении новых теорий. В большинстве случаев законы сохранения не способны дать столь полного описания явлений, какое дают фундаментальные законы, а лишь накладывают определенные запреты на реализацию тех или иных состояний при эволюции системы.
Связь законов сохранения с симметрией системы.
Ответ на естественный вопрос о том, почему справедливы законы сохранения в физике был найден сравнительно недавно. Оказалось, что законы сохранения возникают в системах при наличии у них определенных элементов симметрии. (Элементом симметрии системы называется любое преобразование, переводящие систему в себя, т.е. не изменяющее ее. Например элементом симметрии квадрата является поворот на прямой угол вокруг оси, проходящей через его центр - “ось вращения четвертого порядка”).
Глобальные законы сохранения связаны с существованием таких преобразований, которые оставляют неизменными любую систему. К ним относятся:
Закон сохранения энергии, являющийся следствием симметрии относительно сдвига во времени (однородности времени).
Закон сохранения импульса, являющийся следствием симметрии относительно параллельного переноса в пространстве (однородности пространства).
Закон сохранения момента импульса, являющийся следствием симметрии относительно поворотов в пространстве (изотропности пространства).
Закон сохранения заряда, являющийся следствием симметрии относительно замены описывающих систему комплексных параметров на их комплексно сопряженные значения.
Закон сохранения четности, являющийся следствием симметрии относительно операции инверсии (“отражения в зеркале”, меняющего “право” на “лево”).
Закон сохранения энтропии, являющийся следствием симметрии относительно обращения времени.
Кратко рассмотрим законы сохранения механических величин.
Закон сохранения импульса. Каждой материальной точке с массой m, движущейся со скоростью V, приписывается векторная характеристика - импульс, определяемый как произведение Массы на скорость:
(1) .
Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил:
(2) .
В случае системы материальных точек (совокупностью которых можно считать любое реальное тело) полный импульс определяется как векторная сумма всех импульсов
(3) ,
Скорость изменения полного импульса определяется суммой внешних сил, действующих на систему (т.е. только сил, описывающих взаимодействие элементов системы с не принадлежащими ей объектами):
(4)
Системы, на которые не действуют внешние силы, называются замкнутыми. В них полный импульс не изменяется во времени. Это свойство находит большое практическое применение, поскольку лежит в основе принципа реактивного движения (рис. .5_1)..
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Однако, этот закон сохранения верен и в случаях, когда Ньютоновская механика неприменима (релятивистская физика, квантовая механика). Как отмечалось, он может быть получен как следствие интуитивно-верного утверждения о том, что свойства нашего мира не изменятся, если все его объекты (или начало отсчета!) переместить на некоторый вектор L. В настоящее время не существует каких-либо экспериментальных фактов, свидетельствующих о невыполнении закона сохранения импульса.
Закон сохранения момента импульса. Если понятие импульса в классической механике характеризует поступательное движение тел, момент импульса вводится для характеристики вращения. В случае материальной точки, обладающей импульсом p, положение которой задается радиус-вектором R (рис. 5_2), ее момент импульса относительно начала координат равен
(5)
(знаком [,] обозначена операция векторного умножения, в результате которой получается вектор, направленный в соотвествии с правилом правой руки в направлении, перпендикулярном перемножаемым векторам, числено равный ). Например, при движении тела по окружности вектор L направлен вдоль ее оси.
Скорость изменения момента импульса определяется моментом силы (произведением силы на “плечо”):
(6) .
Очевидно, что момент импульса сохраняется во времени в случае отсутствия сил или при условии действия сил в направлении R.
Закон сохранения момента импульса является следствием утверждения о том, что свойства окружающего мира не изменяются при поворотах (или повороте системы отсчета) в пространстве.
Момент импульса системы точечных тел L определяется как сумма моментов каждой из точек и сохраняется во времени при условии равенства нулю момента внешних сил.
В случае твердого тела, вращающегося вокруг неподвижной оси, все его точки движутся по окружностям, центры которых лежат на этой оси. Полный момент ориентирован вдоль оси вращения. Т.о. при отсутствии внешних воздействий ось вращения тела вместе с L сохраняет свою ориентацию в пространстве. Это свойство используется в навигационных приборах (гирокомпасах).
В случае неравенства нулю момента силы соотношение (6) предсказывает весьма “необычное” с точки зрения “здравого смысла” поведение быстро вращающихся тел ( их момент импульса направлен по оси вращения) с помещенной на острие осью вращения (рис. 5_3).. Такие тела под действием внешних сил (например, силы тяжести) вместо того, чтобы перемещаться в сторону действия силы, начинают медленно вращаться вокруг острия в перпендикулярной приложенной силе плоскости. Несмотря на то, что подобное поведение является непосредственным следствием законов Ньютона (или еще более общих законов сохранения и симметрии), этот эффект часто не только вызывает удивление у лиц, мало знакомых с точными науками, но и дает им повод рассуждать об “ошибочности современного естествознания вообще и классической физики в частности. Основанный на принципе “...если я не понимаю теории или наблюдаемого эффекта, то тем хуже для них...”, к сожалению до сих пор все еще популярен, хотя уже на протяжении нескольких столетий развивающееся естествознание демонстрирует его весьма низкую эвристическую эффективность.
Закон сохранения механической энергии утверждает, что сумма кинетических и потенциальных энергий элементов системы не изменяется во времени при условии, что в системе действуют только потенциальные (консервативные) силы. Этот закон механики является частным случаем более общего закона сохранения энергии, выполняющегося в любой замкнутой (изолированной от внешнего мира) системе. Формулировка закона сохранения энергии обладает меньшей наглядностью по сравнению с законами сохранения импульса и момента, поскольку для понятия энергии по-видимому невозможно дать исчерпывающего определения даже в рамках классического естествознания. При взаимодействиях между телами энергия может переходить из одной формы в другую и описываться совершенно непохожими друг на друга математическими выражениями. В результате развития естествознания неоднократно открывались новые формы энергии, смысл этого понятия уточнялся.
Первоначально в механике были введены кинетическая энергия (обусловленная движением тела)
(7) ,
и потенциальная (обусловленная взаимодействиями между телами и зависящая от их расположения в пространстве) - U(R). Конкретное математическое выражение для U(R) определяется взаимодействиями между объектами. В большинстве механических систем механическая энергия (сумма K+U) сохраняется во времени (напр. в случае мяча, упруго ударяющегося о пол). Однако нередки и такие системы, в которых механическая энергия изменяется (чаще всего убывает). Для описания этого были введены диссипативные силы (напр. силы вязкого и сухого трения и др.). Со временем выяснилось, что диссипативные силы описывают не исчезновение или возникновение механической энергии, а переходы ее в другие формы (тепловую, электромагнитную, энергию связи и т.д.). История развития естествознания знает несколько примеров того, как кажущееся нарушение закона сохранения энергии стимулировало поиск ранее неизвестных каналов ее преобразования, что в результате приводило к открытию ее новых форм (так, например, “безвозвратная” потеря энергии в некоторых реакциях с участием элементарных частиц послужила указанием на существование еще одной неизвестной ранее элементарной частицы, впоследствии получившей название нейтрино).
Закон сохранения энергии имеет большое практическое значение, поскольку существенно ограничивает число возможных каналов эволюции системы без ее детального анализа(рис. 5_4). Так на основании этого закона оказывается возможным априорно отвергнуть любой весьма проект весьма экономически привлекательного вечного двигателя первого рода (устройства, способного совершать работу, превосходящую необходимые для его функционирования затраты энергии).
Обсуждение смысла оставшихся глобальных законов сохранения требует уяснения менее широко известных концепций современной физики и будет осуществлено ниже в соответствующих разделах настоящего курса.

Нравится материал? Поддержи автора!
Ещё документы из категории наука, техника:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ